Inventando uma bicicleta ou escrevendo um perceptron em C ++. Parte 3

Vamos implementar o treinamento de um perceptron multicamadas em C ++ usando o método backpropagation.

Prefácio

Olá a todos!) Antes de entrarmos na base deste artigo, gostaria de dizer algumas palavras sobre as partes anteriores. A implementação que propus é uma paródia da RAM do computador, tk. um vetor tridimensional estupra a memória com uma abundância de células vazias, para as quais a memória também está reservada. Portanto, o método está longe de ser o melhor, mas espero que ajude os programadores iniciantes nesta área a entender o que está “sob o capô” das redes neurais mais simples. Desta vez. Ao descrever a função de ativação na primeira parte, cometi um erro - a função de ativação não precisa ser limitada na faixa de valores. Tudo depende dos objetivos do programador. A única condição é que a função deve ser definida em todo o eixo numérico. São dois

Introdução

-, . backpropagation — . , !

: habr.com/ru/post/514372

backpropagation — .

, , , .

:

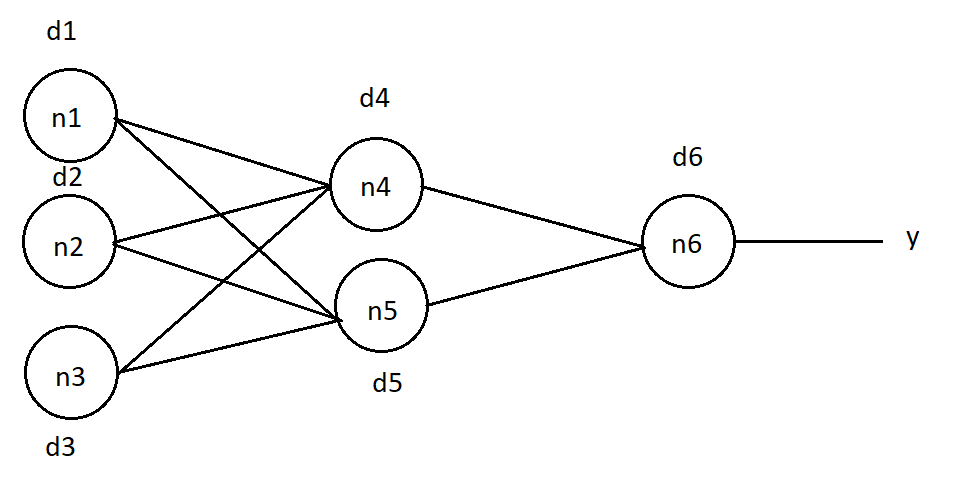
, , . , , . , , . : $$$d j ​ =f(net j ​ )(1−f(net j ​ )) k ∑ ​ d k ​ w kj ​$ (1), j — , , k — , , .. .

, . "O". n6 d6 = (O — y)*( f(in) )*(1 — f(in) ) (2), in —

n6, f(in) — .

(1), . n4 :

d4 = d6 * w46 *( f(in4) ) * (1 — f(in4)), w46 — n4 n6, in4 — n4.

d5 = d6 * w56 *( f(in5) ) * (1 — f(in5)), n5.

d1 = (d4 * w14 + d5 * w15) *( f(in1) ) * (1 — f(in1)), n1, , — .

n2 n3 :

d2 = (d4 * w24 + d5 * w25) *( f(in2) ) * (1 — f(in2))

d3 = (d4 * w34 + d5 * w35) *( f(in3) ) * (1 — f(in3))

, , :

Δw46 = d6 * A * f(in4), w46 — n4 n6 , f(in4) — n4, A — , — , .

Δw56 = d6 * A * f(in5), n5 n6.

:

Δw14 = d4 * A * f(in1)

Δw24 = d4 * A * f(in2)

Δw34 = d4 * A * f(in3)

Δw15 = d4 * A * f(in1)

Δw25 = d4 * A * f(in2)

Δw35 = d4 * A * f(in3)

? . .

void NeuralNet::learnBackpropagation(double* data, double* ans, double acs, double k) {  //data -   , ans -     , k -   , acs-  

, - :

for (uint32_t e = 0; e < k; e++) {
		double* errors = new double[neuronsInLayers[numLayers - 1]]; //      
                // "Do_it"    "Forward"
		Forward(neuronsInLayers[0], data);//    
		getResult(neuronsInLayers[numLayers - 1], errors);//     

:

for (uint16_t n = 0; n < neuronsInLayers[numLayers - 1]; n++) {
			neurons[n][2][numLayers - 1] = (ans[n] - neurons[n][1][numLayers - 1]) * (neurons[n][1][numLayers - 1]) * (1 - neurons[n][1][numLayers - 1]);
		}

, :

for (uint8_t L = numLayers - 2; L > 0; L--) {
			for (uint16_t neu = 0; neu < neuronsInLayers[L]; neu++) {
				for (uint16_t lastN = 0; lastN < neuronsInLayers[L + 1]; lastN++) {
					neurons[neu][2][L] += neurons[lastN][2][L + 1] * weights[neu][lastN][L] * neurons[neu][1][L] * (1 - neurons[neu][1][L]);
					weights[neu][lastN][L] += neurons[neu][1][L] * neurons[lastN][2][L + 1] * acs;
				}
			}
		}

:

void NeuralNet::learnBackpropagation(double* data, double* ans, double acs, double k) {  //k -    acs-  
	for (uint32_t e = 0; e < k; e++) {
		double* errors = new double[neuronsInLayers[numLayers - 1]];
		Forward(neuronsInLayers[0], data);
		getResult(neuronsInLayers[numLayers - 1], errors);
		for (uint16_t n = 0; n < neuronsInLayers[numLayers - 1]; n++) {
			neurons[n][2][numLayers - 1] = (ans[n] - neurons[n][1][numLayers - 1]) * (neurons[n][1][numLayers - 1]) * (1 - neurons[n][1][numLayers - 1]);
		}
		for (uint8_t L = numLayers - 2; L > 0; L--) {
			for (uint16_t neu = 0; neu < neuronsInLayers[L]; neu++) {
				for (uint16_t lastN = 0; lastN < neuronsInLayers[L + 1]; lastN++) {
					neurons[neu][2][L] += neurons[lastN][2][L + 1] * weights[neu][lastN][L] * neurons[neu][1][L] * (1 - neurons[neu][1][L]);
					weights[neu][lastN][L] += neurons[neu][1][L] * neurons[lastN][2][L + 1] * acs;
				}
			}
		}
	}
}

. :

#include <stdio.h>
#include "neuro.h"
int main()
{
    
    uint16_t neurons[3] = {16, 32, 10}; //        , -       
/*        ""  
        
*/
    NeuralNet net(3, neurons);
    double teach[4 * 4] = {//  ""  "4"  , - : 4*4 = 16
        1,0,1,0,
        1,1,1,0,
        0,0,1,0,
        0,0,1,0,
    };
    double test[4 * 4] = {//  "4",  -
        1,0,0,1,
        1,1,1,1,
        0,0,0,1,
        0,0,0,1,
    };
    double ans[10] = {0, 0, 0, 0, 1, 0, 0, 0, 0, 0,};//       , "1"    ,       "4"
    double output[10] = { 0 };//      
    net.Forward(4*4, teach); //    
    net.getResult(10, output); 
    for (uint8_t i = 0; i < 10; i++) printf("%d: %f \n", i, output[i]*100); //  
    net.learnBackpropagation(teach, ans, 0.50, 1000); //    "test",  : 0.5
    printf("\n");
    net.Forward(4 * 4, test);//     
    net.getResult(10, output);
    for (uint8_t i = 0; i < 10; i++) printf("%d: %f \n", i, output[i]*100);
    return 0;
}

:

( ), , 0 9. . , «4»

, , - , . . . , , .

...

. , .

Obrigado pela atenção dispensada a este artigo e pelos comentários sobre a publicação anterior. Vou duplicar o link para os arquivos da biblioteca.

Deixe seus comentários, sugestões. Até logo!