
Aqui está uma tabela (20x20) com um número inteiro de 0 a 99 em cada uma das células.
A tarefa é encontrar 4 números adjacentes sem quebrar a cadeia, um após o outro, com o maior produto. Variantes diferentes de 4 números vizinhos são destacados em cores (dois números são considerados adjacentes se eles estiverem localizados a não mais de 1 célula um do outro).
Hoje vamos implementar o algoritmo de busca em C #.
Primeiro, vamos criar uma matriz bidimensional de 20x20 e gravá-la em um arquivo:
static void CreateArrayFile()
{
Random random = new Random();
string file = "";
for (int i = 0; i < 20; i++)
{
string line = "";
for (int j = 0; j < 20; j++)
{
line += random.Next(0, 99) + ",";
}
line = line + Environment.NewLine;
file += line;
}
using (FileStream fstream = new FileStream($"array.txt", FileMode.OpenOrCreate))
{
byte[] array = System.Text.Encoding.Default.GetBytes(file);
fstream.Write(array, 0, array.Length);
Console.WriteLine(" ");
}
}

Agora podemos escrever os números do arquivo em uma matriz bidimensional.
string[] lines = arrayFile.Split(Environment.NewLine);
for (int i = 0; i < 20; i++)
{
string[] items = lines[i].Split(',');
for (int j = 0; j < 20; j++)
{
table[i, j] = Convert.ToInt32(items[j]);
}
}
Vamos criar uma classe Element para representar as coordenadas e o valor de um número:
public class Element
{
public int Line { get; set; }
public int Column { get; set; }
public int Value { get; set; }
}
De acordo com as condições do problema, é necessário encontrar uma combinação de obras. Vamos implementar a classe Multiplicação para representar uma combinação contendo uma matriz de números e o valor do produto dos números na combinação.
public class Multiplication
{
public Multiplication()
{
Elements = new Element[4];
}
public Element[] Elements { get; set; }
public int Value
{
get
{
Multiply();
return value;
}
}
int value;
void Multiply()
{
if(Elements[0] != null && Elements[1] != null && Elements[2] != null && Elements[3] != null)
{
value = Elements[0].Value * Elements[1].Value * Elements[2].Value * Elements[3].Value;
}
}
}
A primeira coisa a fazer é encontrar os vizinhos mais próximos do número. Por exemplo, para o número 40 em nosso caso, os seguintes vizinhos:
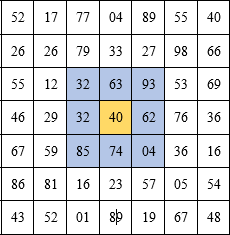
E o número 48 no canto inferior direito tem apenas 3 vizinhos. Não é difícil entender que os vizinhos de qualquer número são:
table[i-1][j-1]
table[i-1][j]
table[i-1][j+1]
table[i][j-1]
table[i][j+1]
table[i+1][j-1]
table[i+1][j]
table[i+1][j+1]
Depois de nos certificarmos de que o índice não está fora dos limites, obtemos o método FindNeighbors que retorna uma coleção de todos os vizinhos mais próximos de um determinado número.
De acordo com a declaração do problema, precisamos encontrar uma combinação de 4 números adjacentes. Para fazer isso, precisamos de um método para encontrar todas as combinações possíveis de 4 números:
static List<Multiplication> GetFactorCombinations(int line, int column)
{
List<Multiplication> combinations = new List<Multiplication>();
if (table[line, column] != 0)
{
List<Element> firstLevelNeighbors = FindNeighbors(line, column);
foreach (var firstLevelNeighbor in firstLevelNeighbors)
{
Element[] elements = new Element[4];
elements[0] = new Element
{
Line = line,
Column = column,
Value = table[line, column]
};
elements[1] = firstLevelNeighbor;
List<Element> secondLevelNeighbors = FindNeighbors(firstLevelNeighbor.Line, firstLevelNeighbor.Column);
foreach (var secondLevelNeighbor in secondLevelNeighbors)
{
if (!elements[0].Equals(secondLevelNeighbor) && !elements[1].Equals(secondLevelNeighbor))
{
elements[2] = secondLevelNeighbor;
}
if (elements[2] != null)
{
List<Element> thirdLevelNeighbors = FindNeighbors(secondLevelNeighbor.Line, secondLevelNeighbor.Column);
foreach (var thirdLevelNeighbor in thirdLevelNeighbors)
{
if (!elements[0].Equals(thirdLevelNeighbor) && !elements[1].Equals(thirdLevelNeighbor) && !elements[2].Equals(thirdLevelNeighbor))
{
elements[3] = thirdLevelNeighbor;
Multiplication multiplication = new Multiplication
{
Elements = elements
};
if (combinations.Where(p=>p.Elements[0].Value==elements[0].Value&& p.Elements[1].Value == elements[1].Value && p.Elements[2].Value == elements[2].Value && p.Elements[3].Value == elements[3].Value).FirstOrDefault()==null)
{
var nnnn =new Multiplication
{
Elements = new Element[] { elements[0], elements[1], elements[2], elements[3]}
};
combinations.Add(nnnn);
}
}
}
}
}
}
}
return combinations;
}
O método obtém as coordenadas de um número na tabela e verifica o valor desse número por 0 (ao multiplicar qualquer número por 0, sempre resulta ser 0). Em seguida, o método pesquisa todos os vizinhos do número fornecido. Nós iteramos sobre os vizinhos do primeiro nível, se o número não for 0, estamos procurando por todos os vizinhos do segundo nível ...
Substituímos o método Equals para comparar os números:
public override bool Equals(Object obj)
{
if (this==null || (obj == null) || !this.GetType().Equals(obj.GetType()))
{
return false;
}
else if(Line == ((Element)obj).Line && Column == ((Element)obj).Column)
{
return true;
}
else
{
return false;
}
}
Continuamos a busca até os vizinhos do quarto nível, se os números não forem duplicados, então os adicionamos à nossa coleção.
if (!elements[0].Equals(thirdLevelNeighbor) && !elements[1].Equals(thirdLevelNeighbor) && !elements[2].Equals(thirdLevelNeighbor))
{
elements[3] = thirdLevelNeighbor;
Multiplication multiplication = new Multiplication
{
Elements = elements
};
if (combinations.Where(p=>p.Elements[0].Value==elements[0].Value&& p.Elements[1].Value == elements[1].Value && p.Elements[2].Value == elements[2].Value && p.Elements[3].Value == elements[3].Value).FirstOrDefault()==null)
{
var combination=new Multiplication
{
Elements = new Element[] { elements[0], elements[1], elements[2], elements[3]}
};
combinations.Add(combination);
}
}
O método GetFactorCombinations pode ser visualizado da seguinte forma:

Agora, percorrendo nosso array bidimensional, estamos procurando a maior combinação de números.
for (int i = 0; i < 20; i++)
{
for (int j = 0; j < 20; j++)
{
List<Multiplication> combinations = GetFactorCombinations(i, j);
foreach (var combination in combinations)
{
if (combination.Value > maxMultiplication.Value)
{
Console.WriteLine(" " + combination.Elements[0].Value + " * " + combination.Elements[1].Value + " * " + combination.Elements[2].Value + " * " + combination.Elements[3].Value + " = " + combination.Value);
maxMultiplication = combination;
}
}
}
}
Console.WriteLine(" = " + maxMultiplication.Elements[0].Value + " * " + maxMultiplication.Elements[1].Value + " * " + maxMultiplication.Elements[2].Value + " * " + maxMultiplication.Elements[3].Value + " = " + maxMultiplication.Value);
Se a próxima combinação for maior que maxMultiplication, reescreva-a.
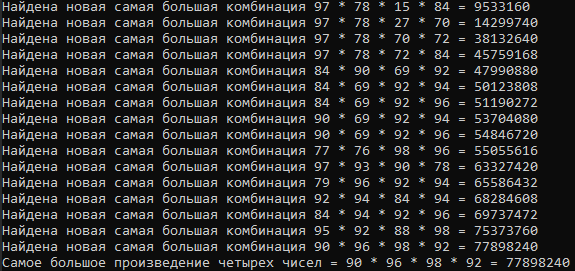
Sim, nós fizemo-lo. Encontramos a combinação de 4 números com o maior produto.
Na verdade, resolvemos o problema, mas o código é codificado para condições específicas, um método puramente procedimental. E se precisarmos pesquisar em uma matriz não 20 por 20, mas, por exemplo, 30 por 30 e uma combinação de não 4, mas 5 números? cada vez que adicionar outro loop aninhado (para iterar tudo com todos) ... Reservamos
2 constantes para o tamanho da tabela e para o tamanho da combinação desejada:
const int TABLE_SIZE = 20;
public const int COMBINATION_SIZE = 4;
Vamos reescrever o método GetFactorCombinations em um método recursivo:
static List<Multiplication> GetMultiplicationForStep(int line, int column, List<Element> otherElements = null)
{
List<Multiplication> resultMultiplications = new List<Multiplication>();
List<Element> resultElements = new List<Element>();
Element element = new Element
{
Column = column,
Line = line,
Value = table[line, column]
};
if (otherElements == null)
{
otherElements = new List<Element>();
}
if(otherElements!=null)
{
resultElements.AddRange(otherElements);
}
if (table[line, column] != 0)
{
if (otherElements.Where(p => p.Equals(element)).FirstOrDefault() == null)
{
resultElements.Add(element);
}
}
if (resultElements.Count() == COMBINATION_SIZE)
{
Multiplication multiplication = new Multiplication
{
Elements = resultElements.ToArray()
};
resultMultiplications.Add(multiplication);
}
else
{
List<Element> elementNeighbors = FindNeighbors(line, column);
elementNeighbors = elementNeighbors.Where(p => !p.Equals(element)&& otherElements.Where(p=>p.Equals(element)).FirstOrDefault()==null).ToList();
List<Multiplication> newMultiplications = new List<Multiplication>();
foreach(Element neighbor in elementNeighbors)
{
// COMBINATION_SIZE ...
newMultiplications.AddRange(GetMultiplicationForStep(neighbor.Line, neighbor.Column, resultElements).Where(p=>p!=null));
}
foreach(Multiplication multiplication in newMultiplications)
{
if(resultMultiplications.Where(p=>p.Value==multiplication.Value).FirstOrDefault()==null)
{
resultMultiplications.Add(multiplication);
}
}
}
return resultMultiplications;
}
O método funciona de acordo com o mesmo princípio de antes, mas em vez de loops aninhados, continuamos a pesquisar os vizinhos recursivamente até que o número de elementos encontrados seja resultElements.Count ()! = COMBINATION_SIZE
Depois de encontrar a combinação, você pode exibi-la lindamente no console:
for (int i = 0; i < TABLE_SIZE; i++)
{
for (int j = 0; j < TABLE_SIZE; j++)
{
if (maxMultiplication.Elements.Where(p => p.Line == i && p.Column == j).FirstOrDefault() != null)
{
Console.BackgroundColor = ConsoleColor.White;
Console.ForegroundColor = ConsoleColor.Black; // ,
Console.Write(table[i, j] + " ");
Console.ResetColor();
}
else
{
Console.Write(table[i, j] + " ");
}
}
Console.WriteLine();
}
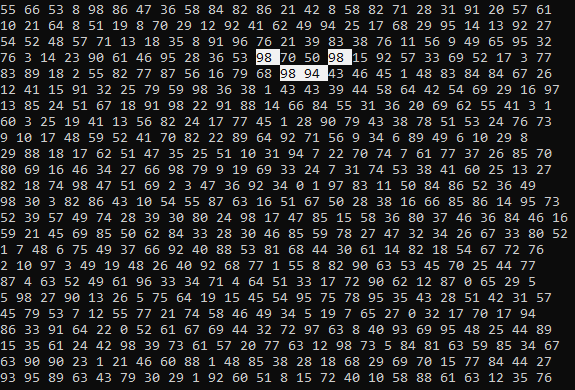
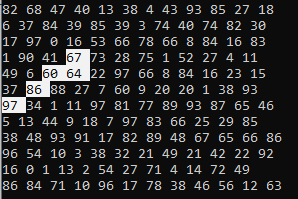
Conclusão
Neste artigo, conhecemos uma das opções para encontrar combinações adjacentes na tabela NxN.
O que mais você pode fazer:
- Você pode considerar se livrar de várias iterações de todas as combinações com all e de outras maneiras para otimizar o código.
- Com base no algoritmo existente, implemente uma busca por combinações de números adjacentes em uma matriz tridimensional. Mas já é outra hora ...
