A matemática da distância social é uma aula de geometria

O desafio de como reabrir com segurança escritórios, escolas e outros locais públicos, mantendo as pessoas a um metro e meio de distância, se resume a uma questão que os matemáticos vêm estudando há séculos.

Pode parecer que um tópico como o empacotamento de esferas agradará apenas aos matemáticos. Quem mais estaria interessado em procurar as maneiras mais eficazes de colocar círculos em um plano ou esferas no espaço?



No entanto, hoje milhões de pessoas em todo o mundo estão pensando precisamente nessa tarefa.



Determinar como abrir edifícios e espaços públicos com segurança, mantendo a distância social é, em particular, um exercício de geometria. Se cada pessoa deve estar a pelo menos um metro e meio de distância de outras pessoas, para calcular quantas pessoas podem se sentar na sala de aula ou na sala de jantar, você precisa colocar círculos não sobrepostos na planta baixa.







Naturalmente, para combater o coronavírus, muitos mais problemas precisam ser resolvidos do que este geométrico. No entanto, o empacotamento de círculos e esferas desempenha um papel nisso - assim como a modelagem de estruturas cristalinas em química e espaços de mensagem abstratos na teoria da informação. Esta tarefa, aparentemente simples na descrição, ocupou as mentes dos maiores matemáticos da história, e as pesquisas mais interessantes nesta área são realizadas hoje, em particular, em dimensões superiores. Por exemplo, matemáticos descobriram recentemente a melhor maneira de compactar em espaços de 8 e 24 dimensões - uma técnica necessária para otimizar códigos de correção de erros usados ​​em telefones celulares e na comunicação com sondas espaciais. Portanto, vamos dar uma olhada em algumas das complicações inesperadas que surgem quando tentamos preencher um espaço com o formulário mais simples.



Esteja você embalando laranjas em caixas no trabalho ou acomodando alunos com segurança com distanciamento social, o tamanho e a forma do seu recipiente são essenciais para sua tarefa. No entanto, para a maioria dos matemáticos, a teoria do empacotamento de esferas trata de preencher todo o espaço. Em duas dimensões, isso significa cobrir o plano com círculos separados do mesmo tamanho.



Aqui está um exemplo de compactação de círculos em um avião. Parece a vista superior de uma embalagem de refrigerante:







Você pode imaginar como esse padrão se repete em todas as direções, como um ladrilho que foi pavimentado com um plano. Pequenos espaços entre os círculos indicam que o plano não está completamente preenchido, mas no caso de círculos de empacotamento isso deve ser esperado. Estamos interessados ​​em saber que porcentagem do avião está coberta. Essa será a "densidade de embalagem" do método específico.



O método acima é chamado de empacotamento quadrado e por um bom motivo - os centros dos círculos podem ser representados como os vértices dos quadrados.







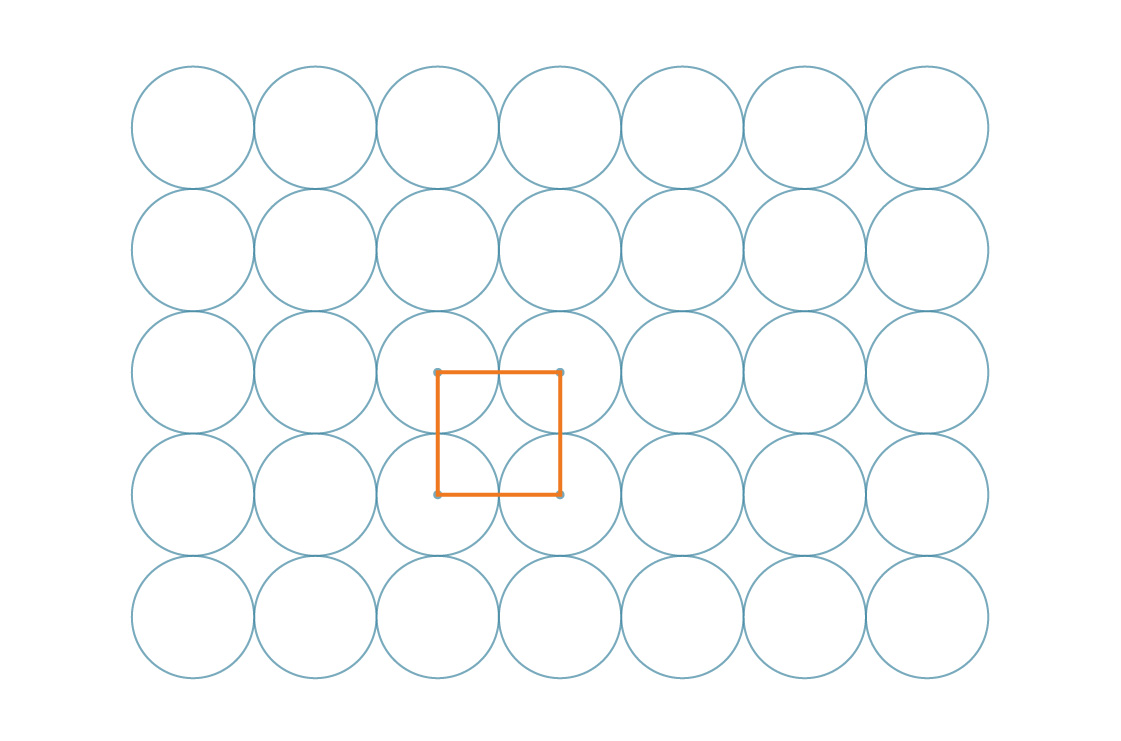
E, de fato, esses próprios quadrados ladrilhavam o plano:







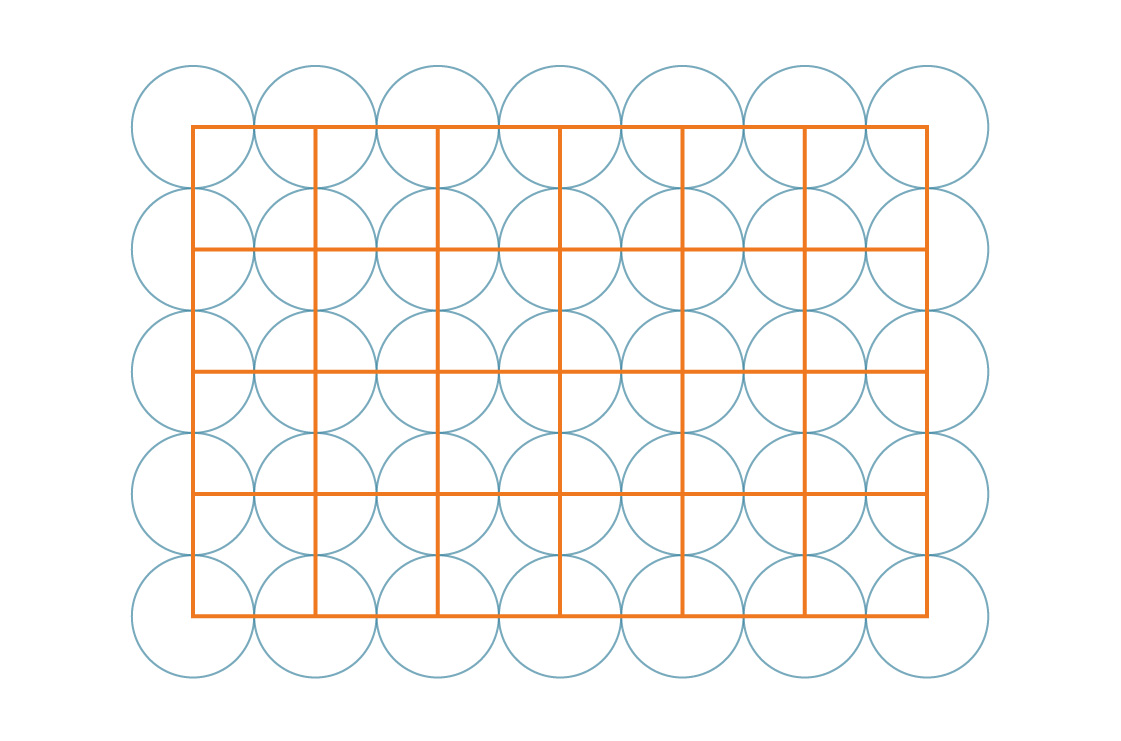
nossa tarefa é facilitada pela simetria do padrão. Como esses quadrados cobrem todo o plano de maneira periódica, a porcentagem do plano coberto pelos círculos é a mesma que a porcentagem do quadrado coberto pelos círculos. Vejamos um desses quadrados.







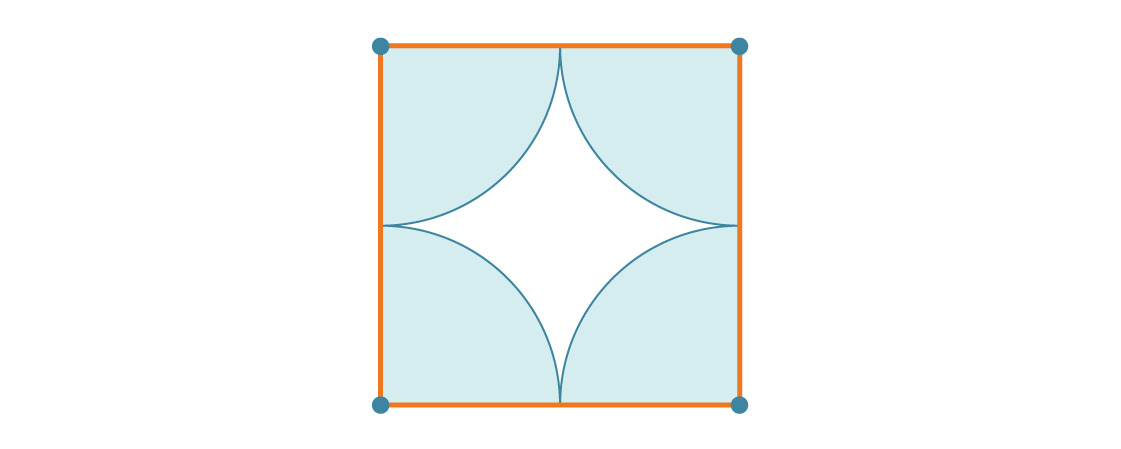
Digamos que o raio do círculo seja r. Isso significa que o comprimento lateral do quadrado é 2r. Em cada um dos vértices do quadrado, há um quarto de um círculo, então a porcentagem de cobertura de cada quadrado é simplesmente igual à razão entre a área de um círculo completo e a área de um quadrado completo:

$$

$$\frac{\pi r^2}{(2r)^2} = \frac{\pi r^2}{4r^2} = \frac{\pi }{4} \approx 0,7854$$

Cada quadrado é cerca de 78,54% coberto por círculos, portanto, considerando o revestimento do avião, é cerca de 78,54% coberto por círculos. Esta é a densidade da embalagem quadrada. Observe que o raio r desapareceu da resposta. E isso faz sentido: não importa o tamanho dos círculos, ainda haverá quatro quartos de um círculo em um quadrado.



Se você tentou dobrar as latas de refrigerante assim, e elas deslizam e preenchem as lacunas, você sabe que há outra maneira de embalar os círculos em um avião:







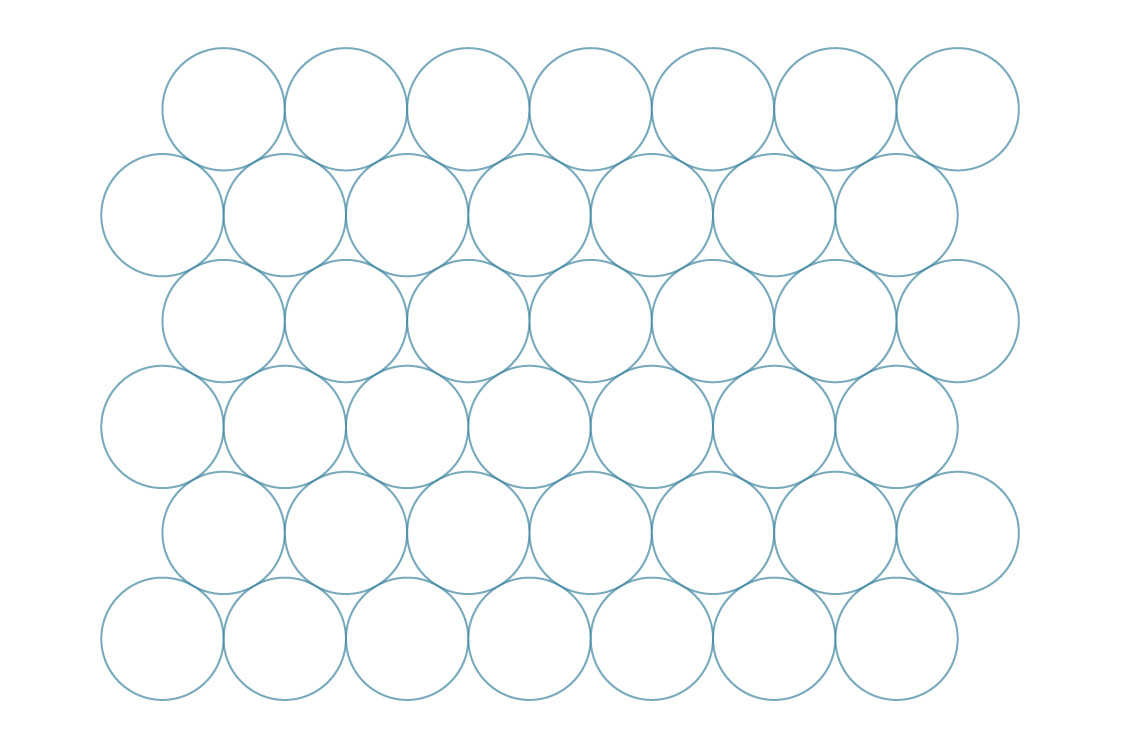
vamos fazer uma abordagem semelhante à anterior e imaginar que os centros dos círculos, neste caso, formam hexágonos regulares ...







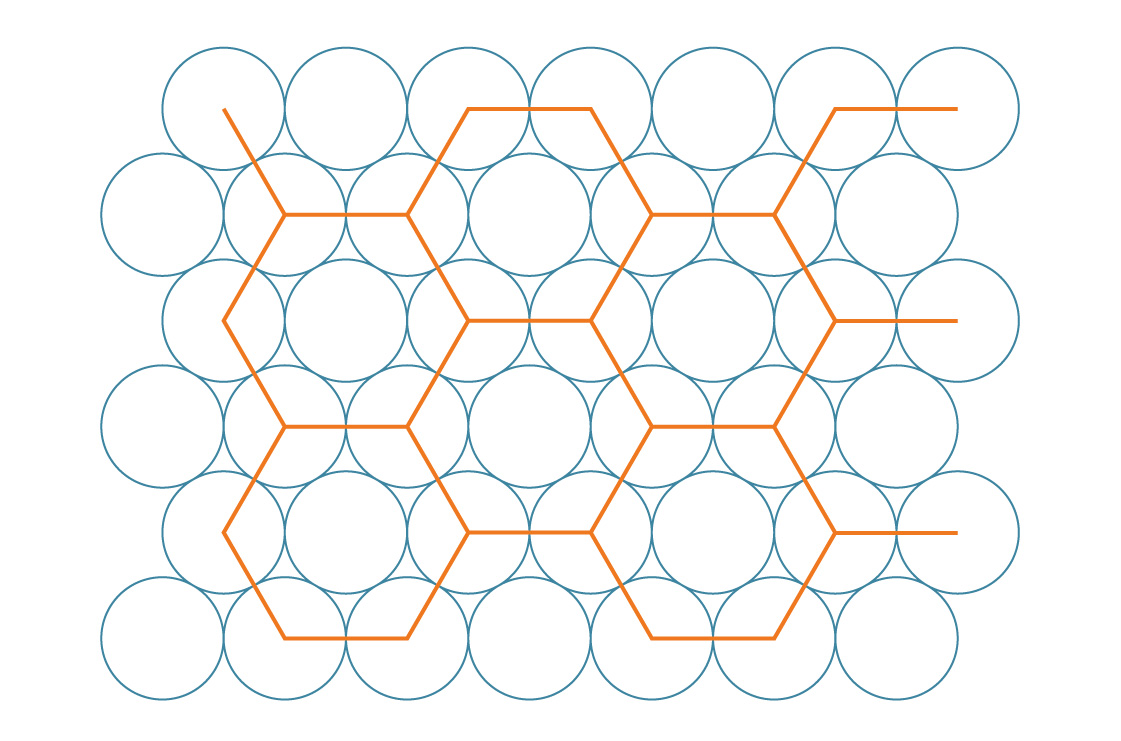
Chamamos isso de empacotamento hexagonal. Parece que esse método preenche as lacunas com mais eficiência do que quadrá-las. Para verificar isso, vamos comparar suas densidades de empacotamento. Os hexágonos, como os quadrados, revestem completamente o plano, de modo que podemos determinar a densidade desse método analisando um único hexágono.







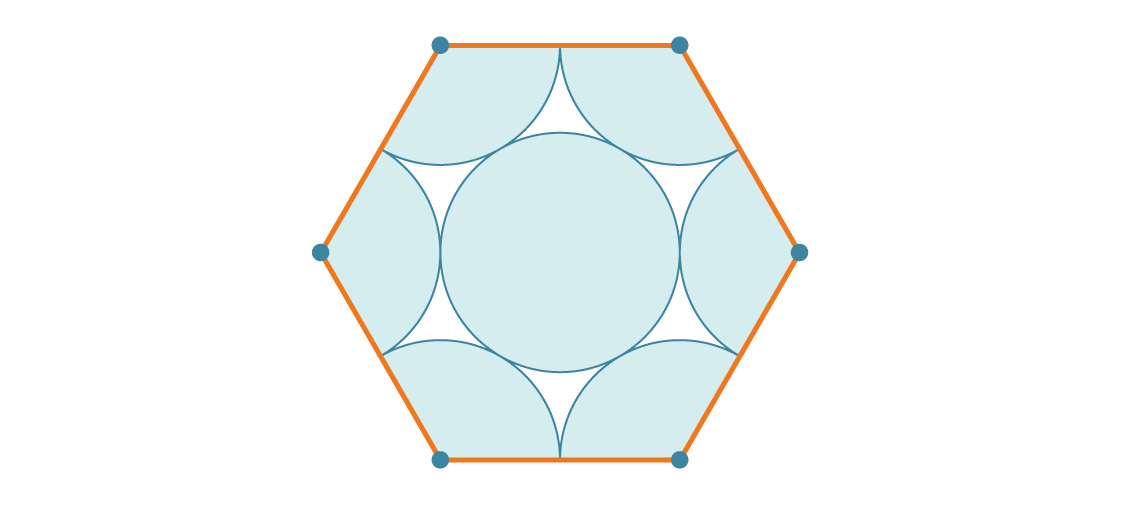
Que parte do hexágono é coberta por círculos? Como um hexágono regular tem um ângulo interno de 120 °, há um terço de um círculo em cada um dos cantos. Acontece dois círculos completos, e o círculo do meio vai em terceiro. Portanto, cada hexágono é coberto por três círculos. Se o raio de cada círculo for r, então a área é 3πr².







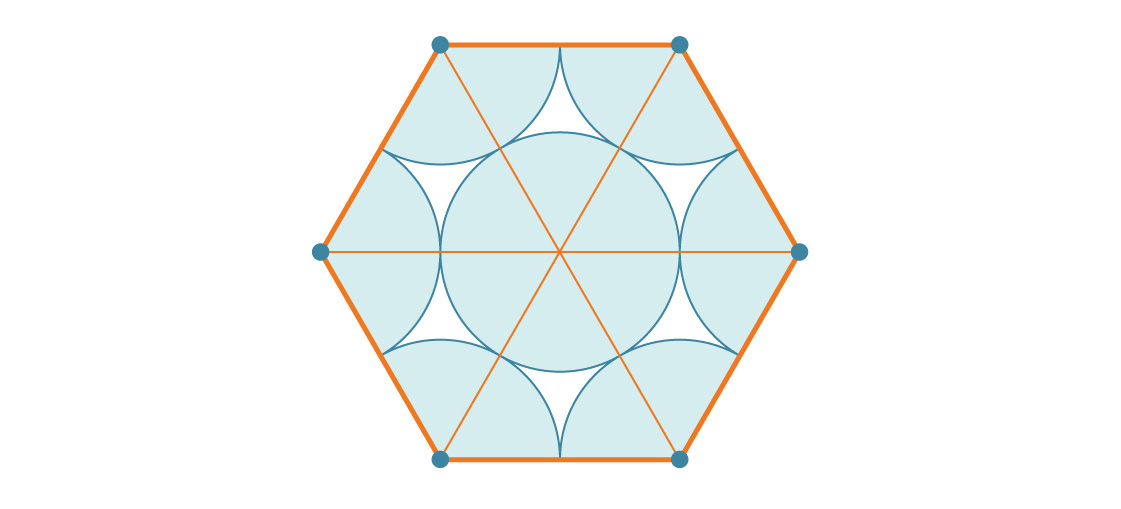
Como isso se compara à área de um hexágono? Um hexágono com comprimento lateral s tem seis triângulos equiláteros com comprimento lateral s, cada um dos quais é s ² √3 / 4. Portanto, a área do hexágono é 6 * s ² √3 / 4 = 6 s ² √3 / 4. Como o comprimento lateral de nosso hexágono é 2r, sua área é:

$$

$$\frac{6 s^2 \sqrt3}{4} = \frac{6 (2r)^2 \sqrt3}{4} = \frac{24 r^2 \sqrt3}{4} = 6 r^2 \sqrt3$$

Agora você pode calcular a porcentagem do hexágono coberto pelos círculos (dividindo a área dos seis círculos pela área do hexágono):

$$

$$\frac{3 \pi r^2}{6 r^2 \sqrt3} = \frac{3 \pi}{6 \sqrt3} = \frac{\pi}{2 \sqrt3} \approx 0,9069$$

Cada hexágono é cerca de 90,69% coberto por círculos, então esta embalagem será muito mais eficiente do que uma quadrada. Observe como o raio do círculo desaparece novamente conforme o esperado. Na verdade, não existe embalagem mais eficiente.



Mas não foi fácil provar. Matemáticos famosos como Joseph Louis Lagrange e Karl Friedrich Gauss começaram a trabalhar nisso no final do século 18 e no início do século 19, mas o problema foi completamente resolvido apenas na década de 1940, pelo processamento cuidadoso de todos os arranjos possíveis - periódicos e não periódicos. O fato de ter demorado tanto para resolver o problema em duas dimensões, onde tudo é muito fácil de imaginar, pode servir de alerta para o que nos espera nas dimensões superiores.



Empacotar esferas em três dimensões é uma tarefa muito mais difícil, embora tenha algumas semelhanças com seu primo bidimensional. Por exemplo, as embalagens bidimensionais que consideramos consistem em uma camada.







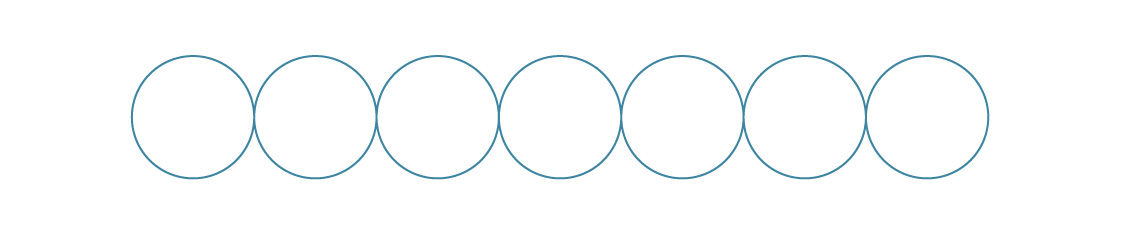
Para um pacote quadrado, colocamos cada camada sobre a anterior.







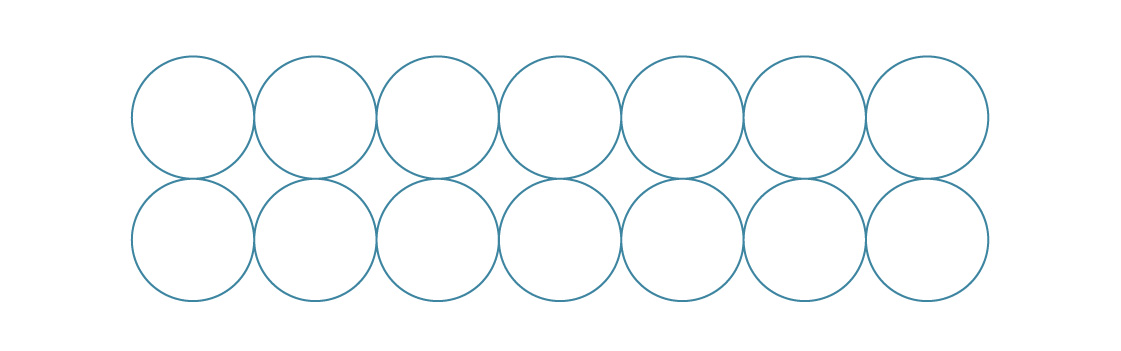
Para o empacotamento hexagonal, colocamos novas camadas entre as anteriores.







Embalagens diferentes são obtidas dependendo de como combinamos cópias de camadas diferentes.



Em três dimensões, esse arranjo de camadas umas sobre as outras cria embalagens fundamentalmente diferentes.







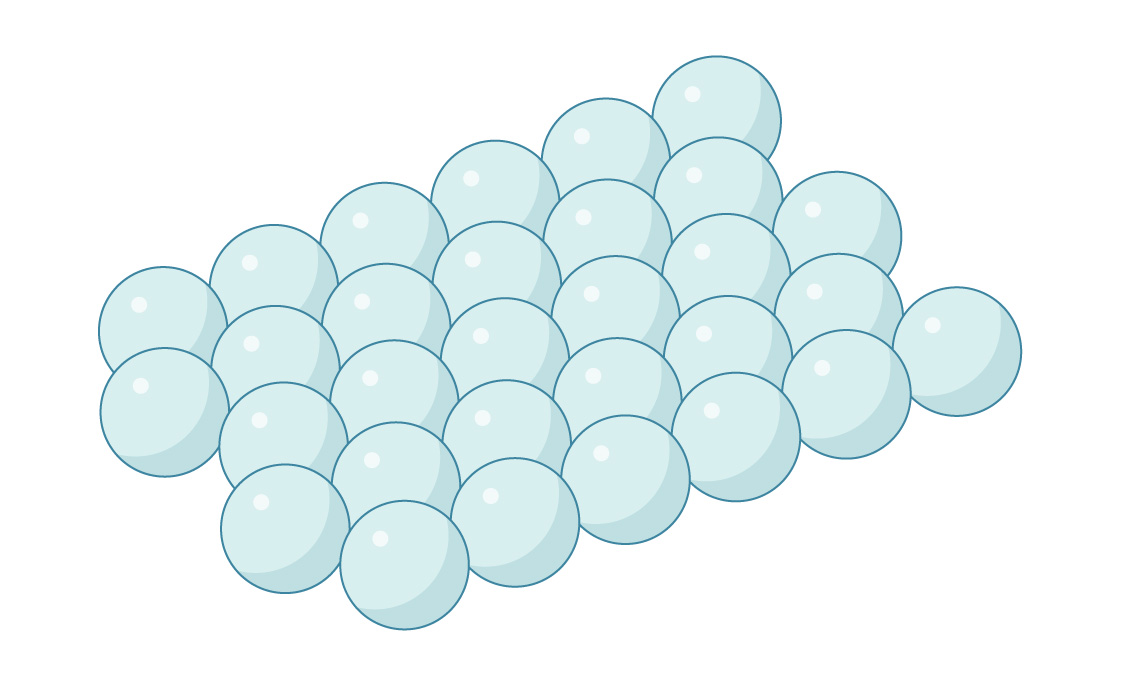
Esta é uma camada de esferas, empacotada hexagonalmente, como sugere o nosso empacotamento ideal de círculos em um plano. Da mesma forma, você pode colocar a segunda camada em cima da primeira colocando esferas nos espaços entre as esferas inferiores.







Mas em três dimensões, a geometria fica um pouco mais complicada. Em cada camada de esferas, a distância entre as lacunas adjacentes acaba sendo menor que a distância entre os centros das esferas. Portanto, você não pode colocar uma esfera em cada lacuna - elas se cruzariam. Portanto, as lacunas nas duas camadas se alinham para criar canais que percorrem o pacote.







Existem duas maneiras de colocar a terceira camada. Você pode alinhar as lacunas com as inferiores e deixar os canais abertos. Aqui está uma vista lateral desse arranjo:







Para manter os canais abertos, você precisa colocar as esferas na terceira camada logo acima das esferas da primeira camada. Esse arranjo de esferas é chamado de "empacotamento hexagonal denso" (silo) e, se você olhar de cima, poderá ver as lacunas abertas passando direto.







Outra opção para colocar a terceira camada é fechar os canais. As esferas na terceira camada são colocadas diretamente acima das lacunas da primeira:







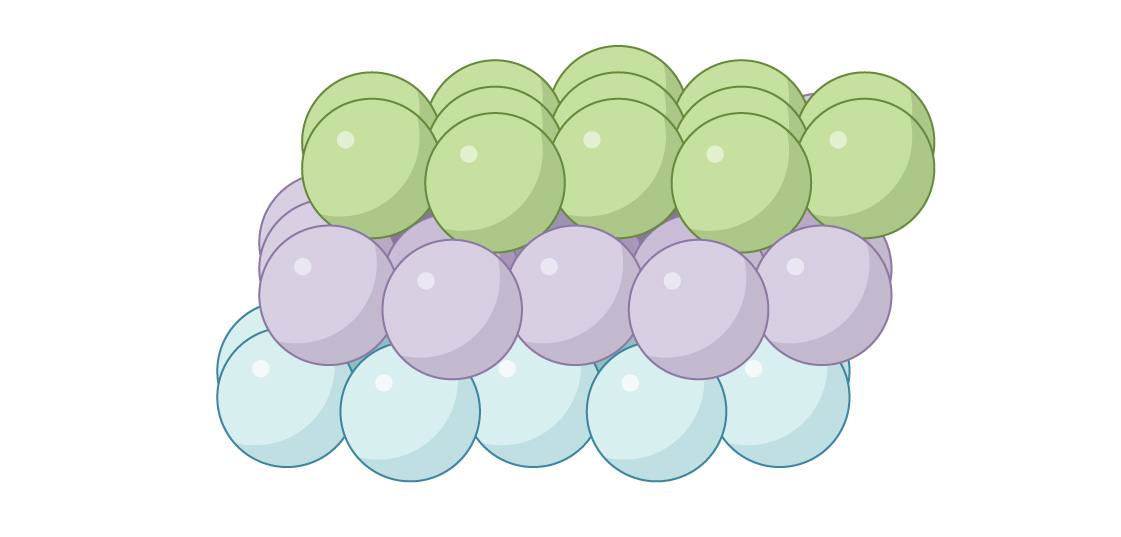
isso é chamado de "cúbica centrada na face" (FCC) ou "embalagem cúbica fechada". Quando visto de cima, não haverá lacunas.







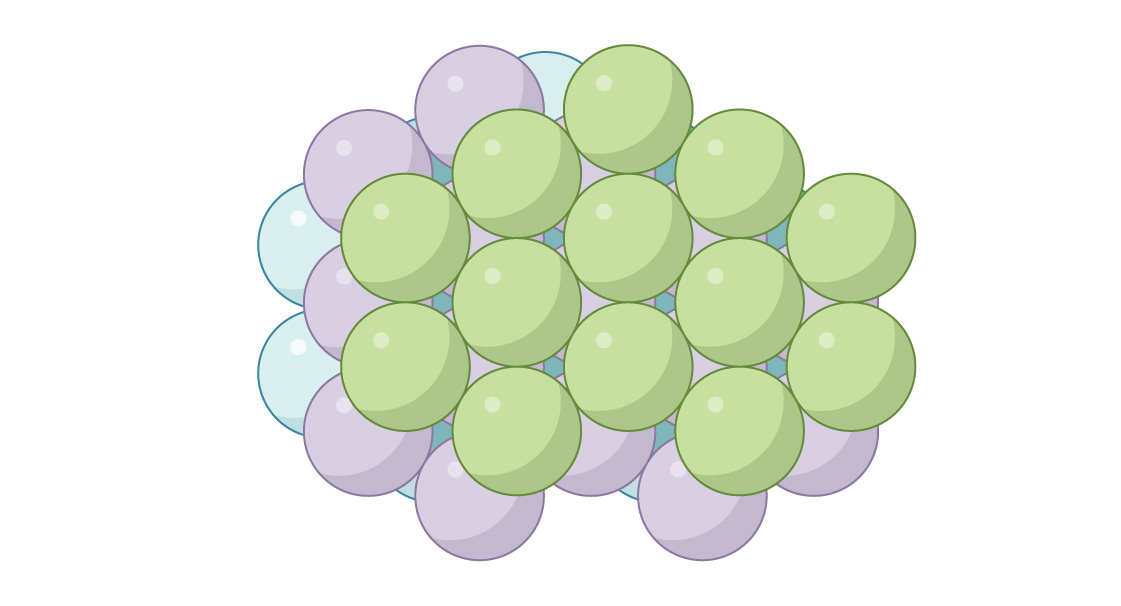
Esses dois arranjos semelhantes, mas fundamentalmente diferentes, surgem na química, descrevendo o arranjo dos átomos em materiais diferentes. Por exemplo, em metais como prata e ouro, a estrutura tem a forma de HA, e em metais como zinco e titânio - silos. Cada um dos dois métodos permite preencher o espaço com esferas. No método do silo, em cada segunda camada as esferas estão localizadas exatamente da mesma forma, e no GK - em cada terceira. Você pode criar um número infinito de embalagens diferentes combinando ambos os métodos, mas é interessante que tanto o silo quanto o GK forneçam um pacote ideal! Sua densidade de empacotamento não é apenas a mesma, π 3√2 ≈ 0,7405 é o empacotamento mais denso possível no espaço tridimensional. O famoso matemático e astrônomo Johannes Kepler sugeriu isso em 1611, mas a prova completaapenas o matemático Thomas Hales foi capaz de deduzir em 1998.







Há mais espaço no espaço 3D e temos mais maneiras de empacotar as esferas de maneira eficaz. Quando você adiciona dimensões, a complexidade da embalagem apenas aumenta - há mais espaço, mais opções e é mais difícil de imaginar. Além disso, as esferas ficam menores em dimensões superiores!







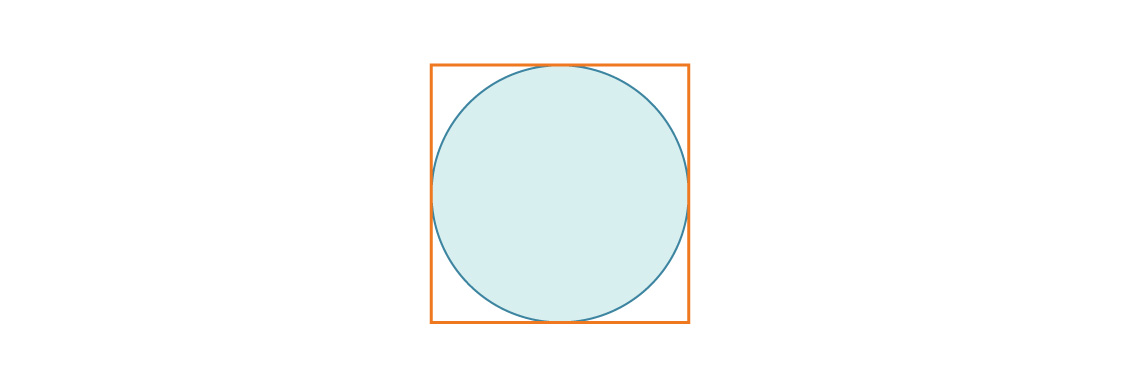
Considere um círculo inscrito em um quadrado com comprimento de lado 1.



O raio do círculo é r = 1/2, então a proporção da área do círculo para a área do quadrado é:

$$

$$\frac{\pi r^2}{s^2} = \frac{\pi (\frac{1}{2})^2}{1^2} = \frac{\pi }{4} \approx 0,7854$$

Que também é igual à densidade de embalagem do quadrado em duas dimensões.



Agora vamos considerar o volume de uma esfera inscrita em um cubo unitário.







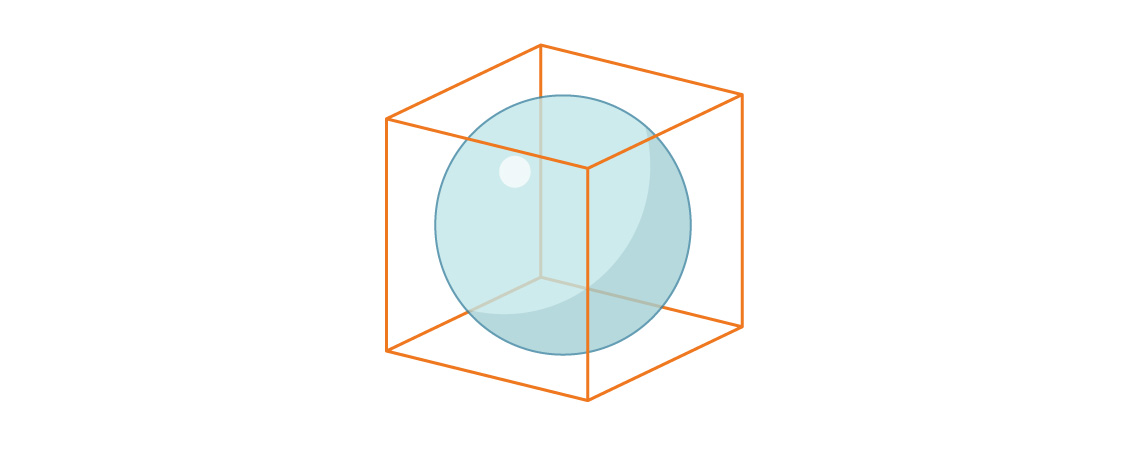
O raio da esfera é novamente igual a r = 1/2, então a razão entre o volume da esfera e o volume do cubo é:

$$

$$\frac{\frac{4}{3}\pi r^3}{s^3} = \frac{\frac{4}{3}\pi (\frac{1}{2})^3}{1^3} = \frac{4}{3}\pi (\frac{1}{8}) = \frac{\pi}{6} \approx 0,5236$$

Observe que a proporção do cubo ocupado pela esfera inscrita em três dimensões é menor que a proporção do quadrado ocupado pelo círculo inscrito em duas dimensões. Esse padrão continua: com dimensões crescentes, essa proporção diminui. À medida que n cresce, as esferas n-dimensionais ocupam cada vez menos espaço n-dimensional.



Isso pode ser mostrado usando álgebra, mas também pode ser entendido se você pensar sobre ângulos. Em qualquer dimensão, uma esfera n-dimensional pode ser inscrita em um cubo n-dimensional. A esfera toca as bordas do cubo, mas não atinge os cantos, então há uma região ao redor de cada canto que está dentro do cubo, mas fora da esfera. No entanto, uma caixa n-dimensional terá 2 ⁿângulos, ou seja, com um aumento em n, o número de áreas não cobertas por uma esfera cresce exponencialmente. Além disso, a distância entre os cantos e a esfera também aumenta. Isso significa que, a longo prazo, o espaço dentro do cubo n-dimensional, mas fora da esfera n-dimensional, simplesmente esmagará o espaço ocupado pela esfera.



Se a contração das esferas parece estranha o suficiente para você, então os matemáticos envolvidos no empacotamento de esferas notaram algo ainda mais inesperado nas dimensões 8 e 24. Nessas dimensões, as esferas encolhem apenas o suficiente para poder preencher as lacunas entre as novas esferas, o que dá um empacotamento ultradenso nessas dimensões ... Foi levantada a hipótese sobre a otimalidade desses métodos especiais, mas não era conhecido exatamente até 2016, quando Marina Vyazovskaya provou este teoremapara espaço de 8 dimensões. Uma semana depois, Vyazovskaya e seus assistentes expandiram seu método para provar o caso do espaço de 24 dimensões também.



Resulta do trabalho de Vyazovskaya que agora conhecemos as maneiras mais eficientes de empacotar esferas nas dimensões 1, 2, 3, 8 e 24. Mas, em outras dimensões, ainda há muito trabalho a ser feito. Então pegue as laranjas e as latas de refrigerante e comece a experimentar. Você pode ser aquele que pode preencher as lacunas importantes.

Exercícios

1. Digamos que começamos a compactar o plano de coordenadas conforme mostrado nas fotos abaixo. O centro do círculo inferior esquerdo está localizado no ponto (0, 0) e o centro do círculo inferior direito está no ponto (2, 0).







Onde está o centro do terceiro círculo?



2. Abaixo está o início do empacotamento "cúbico simples" das esferas. Qual é a densidade de embalagem de tal esquema?







3. Aqui está o começo de compactar o avião em octógonos regulares.







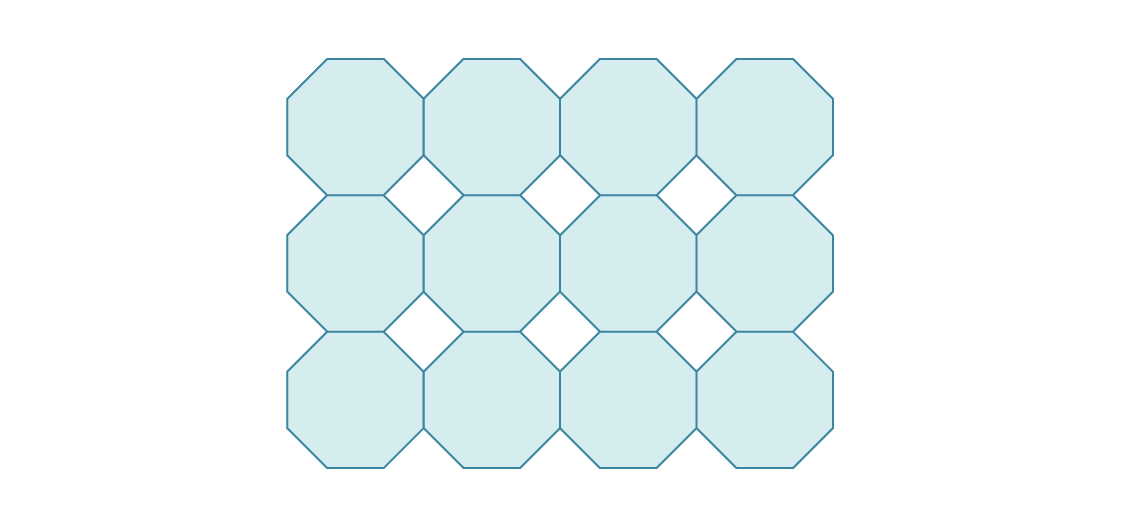
Qual é a densidade desse pacote?

Respostas

Veja também:

• " Google lança Sodar, uma ferramenta de RA para exibir distância social "
• " Meta-estudo revela a eficácia das máscaras e distanciamento contra SARS-CoV-2 (COVID-19) "
• " COVID-19: Epidemic Parametric Prediction Model "