onde q é a carga da partícula, rij é a distância entre as partículas, C é uma constante, dependendo da escolha das unidades de medida. No SI é - , no SGS-1, no meu programa (onde a energia é expressa em elétron-volts, distância em angstroms e carga em cargas elementares) C é aproximadamente igual a 14,3996.
Então, o que você diz? Basta adicionar o termo correspondente ao potencial do par e pronto. No entanto, na maioria das vezes na modelagem de MD, condições periódicas de contorno são usadas, ou seja, o sistema simulado é cercado por todos os lados por um número infinito de suas cópias virtuais. Nesse caso, cada imagem virtual do nosso sistema irá interagir com todas as partículas carregadas dentro do sistema, de acordo com a lei de Coulomb. E como a interação Coulomb diminui muito fracamente com a distância (como 1 / r), não é tão fácil descartá-la, dizendo que não a calculamos a partir de tal e qual distância. Uma série da forma 1 / x diverge, isto é, sua quantidade, em princípio, pode crescer indefinidamente. E agora, você não salga uma tigela de sopa? Isso vai te matar com eletricidade?
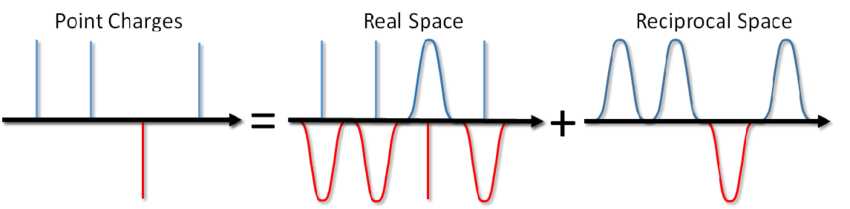
... você pode não apenas salgar a sopa, mas também calcular a energia da interação Coulomb em condições de contorno periódicas. Esse método foi proposto por Ewald em 1921 para calcular a energia de um cristal iônico (você também pode vê-lo na Wikipedia ). A essência do método é rastrear cargas pontuais e subtrair a função de triagem. Nesse caso, uma parte da interação eletrostática é reduzida a uma de ação curta e pode ser simplesmente cortada de maneira padrão. A parte restante de longo alcance é efetivamente somada no espaço de Fourier. Omitindo a conclusão, que pode ser vista no artigo de Blinov ou no mesmo livro de Frenkel e Smith , escreverei imediatamente uma solução chamada a soma de Ewald:
onde α é um parâmetro que regula a razão de cálculos nos espaços dianteiro e reverso, k são vetores no espaço recíproco sobre o qual a soma está ocorrendo, V é o volume do sistema (no espaço dianteiro). A primeira parte (E real ) é de curto alcance e é calculada no mesmo ciclo que os outros potenciais de pares, consulte a função real_ewald no artigo anterior. A última contribuição ( Econst ) é uma correção para a auto-interação e é freqüentemente chamada de "parte constante" porque não depende das coordenadas das partículas. Seu cálculo é trivial, portanto, focaremos apenas a segunda parte da soma de Ewald (E rec), somatório no espaço recíproco. Naturalmente, na época da derivação de Ewald, não havia dinâmica molecular; não consegui descobrir quem primeiro utilizou esse método no MD. Atualmente, qualquer livro sobre MD contém sua apresentação como uma espécie de padrão-ouro. Para reservar, Allen até forneceu código de exemplo no Fortran. Felizmente, ainda tenho o código que já foi escrito em C para a versão sequencial, resta apenas paralelizá-lo (eu me permiti omitir algumas declarações de variáveis e outros detalhes insignificantes):
void ewald_rec()
{
int mmin = 0;
int nmin = 1;
// iexp(x[i] * kx[l]),
double** elc;
double** els;
//... iexp(y[i] * ky[m])
double** emc;
double** ems;
//... iexp(z[i] * kz[n]),
double** enc;
double** ens;
// iexp(x*kx)*iexp(y*ky)
double* lmc;
double* lms;
// q[i] * iexp(x*kx)*iexp(y*ky)*iexp(z*kz)
double* ckc;
double* cks;
//
eng = 0.0;
for (i = 0; i < Nat; i++) //
{
// emc/s[i][0] enc/s[i][0]
// elc/s , .
elc[i][0] = 1.0;
els[i][0] = 0.0;
// iexp(kr)
sincos(twopi * xs[i] * ra, els[i][1], elc[i][1]);
sincos(twopi * ys[i] * rb, ems[i][1], emc[i][1]);
sincos(twopi * zs[i] * rc, ens[i][1], enc[i][1]);
}
// emc/s[i][l] = iexp(y[i]*ky[l]) ,
for (l = 2; l < ky; l++)
for (i = 0; i < Nat; i++)
{
emc[i][l] = emc[i][l - 1] * emc[i][1] - ems[i][l - 1] * ems[i][1];
ems[i][l] = ems[i][l - 1] * emc[i][1] + emc[i][l - 1] * ems[i][1];
}
// enc/s[i][l] = iexp(z[i]*kz[l]) ,
for (l = 2; l < kz; l++)
for (i = 0; i < Nat; i++)
{
enc[i][l] = enc[i][l - 1] * enc[i][1] - ens[i][l - 1] * ens[i][1];
ens[i][l] = ens[i][l - 1] * enc[i][1] + enc[i][l - 1] * ens[i][1];
}
// K-:
for (l = 0; l < kx; l++)
{
rkx = l * twopi * ra;
// exp(ikx[l]) ikx[0]
if (l == 1)
for (i = 0; i < Nat; i++)
{
elc[i][0] = elc[i][1];
els[i][0] = els[i][1];
}
else if (l > 1)
for (i = 0; i < Nat; i++)
{
// iexp(kx[0]) = iexp(kx[0]) * iexp(kx[1])
x = elc[i][0];
elc[i][0] = x * elc[i][1] - els[i][0] * els[i][1];
els[i][0] = els[i][0] * elc[i][1] + x * els[i][1];
}
for (m = mmin; m < ky; m++)
{
rky = m * twopi * rb;
// iexp(kx*x[i]) * iexp(ky*y[i])
if (m >= 0)
for (i = 0; i < Nat; i++)
{
lmc[i] = elc[i][0] * emc[i][m] - els[i][0] * ems[i][m];
lms[i] = els[i][0] * emc[i][m] + ems[i][m] * elc[i][0];
}
else // m :
for (i = 0; i < Nat; i++)
{
lmc[i] = elc[i][0] * emc[i][-m] + els[i][0] * ems[i][-m];
lms[i] = els[i][0] * emc[i][-m] - ems[i][-m] * elc[i][0];
}
for (n = nmin; n < kz; n++)
{
rkz = n * twopi * rc;
rk2 = rkx * rkx + rky * rky + rkz * rkz;
if (rk2 < rkcut2) //
{
// (q[i]*iexp(kr[k]*r[i])) -
sumC = 0; sumS = 0;
if (n >= 0)
for (i = 0; i < Nat; i++)
{
//
ch = charges[types[i]].charge;
ckc[i] = ch * (lmc[i] * enc[i][n] - lms[i] * ens[i][n]);
cks[i] = ch * (lms[i] * enc[i][n] + lmc[i] * ens[i][n]);
sumC += ckc[i];
sumS += cks[i];
}
else // :
for (i = 0; i < Nat; i++)
{
//
ch = charges[types[i]].charge;
ckc[i] = ch * (lmc[i] * enc[i][-n] + lms[i] * ens[i][-n]);
cks[i] = ch * (lms[i] * enc[i][-n] - lmc[i] * ens[i][-n]);
sumC += ckc[i];
sumS += cks[i];
}
//
akk = exp(rk2 * elec->mr4a2) / rk2;
eng += akk * (sumC * sumC + sumS * sumS);
for (i = 0; i < Nat; i++)
{
x = akk * (cks[i] * sumC - ckc[i] * sumS) * C * twopi * 2 * rvol;
fxs[i] += rkx * x;
fys[i] += rky * x;
fzs[i] += rkz * x;
}
}
} // end n-loop (over kz-vectors)
nmin = 1 - kz;
} // end m-loop (over ky-vectors)
mmin = 1 - ky;
} // end l-loop (over kx-vectors)
engElec2 = eng * * twopi * rvol;
}
Algumas explicações para o código: a função calcula o expoente complexo (nos comentários ao código, é indicado iexp para remover a unidade imaginária dos parênteses) do produto vetorial do vetor k e o vetor raio da partícula para todos os vetores k e para todas as partículas. Este expoente é multiplicado pela carga de partículas. Em seguida, é calculada a soma de tais produtos para todas as partículas (a soma interna na fórmula para E rec ); em Frenkel é chamada densidade de carga e em Blinov é chamado fator estrutural. E então, com base nesses fatores estruturais, a energia e as forças que atuam nas partículas são calculadas. Os componentes dos vetores k (2π * l / a, 2π * m / b, 2π * n / c) são caracterizados por três números inteiros l , m e n, que são executados em ciclos até os limites especificados pelo usuário. Os parâmetros a, bec são as dimensões do sistema simulado nas dimensões x, ye z, respectivamente (a conclusão é correta para um sistema com uma geometria retangular paralelepipédica). No código, 1 / a , 1 a / b e 1 / c correspondem às variáveis RA , Rb, e RC . As matrizes para cada valor são apresentadas em duas cópias: para as partes reais e imaginárias. Cada próximo vetor-k em uma dimensão é obtido iterativamente do anterior, multiplicando-se o anterior por um, de modo a não contar o seno com cosseno de cada vez. O EMC / s e enc / s matrizes são preenchidas para todos me n , respectivamente, e a matriz elc / s coloca o valor de cada l > 1 no índice zero de l para economizar memória.
Para fins de paralelização, é vantajoso "reverter" a ordem dos ciclos, para que o ciclo externo corra sobre as partículas. E aqui vemos um problema - essa função pode ser paralelizada apenas antes de calcular a soma de todas as partículas (densidade de carga). Cálculos adicionais são baseados nessa quantidade, e serão calculados somente quando todos os threads terminarem seu trabalho, portanto, é necessário dividir essa função em duas. O primeiro calcula a densidade de carga e o segundo calcula a energia e as forças. Observe que a segunda função exigirá novamente a quantidade q iiexp (kr) para cada partícula e para cada vetor k, calculado na etapa anterior. E aqui há duas abordagens: recalculá-lo novamente ou lembrar-se dele.
A primeira opção leva mais tempo, a segunda - mais memória (número de partículas * número de vetores-k * sizeof (float2)). Eu decidi pela segunda opção:
__global__ void recip_ewald(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the first part : summ (qiexp(kr)) evaluation
{
int i; // for atom loop
int ik; // index of k-vector
int l, m, n;
int mmin = 0;
int nmin = 1;
float tmp, ch;
float rkx, rky, rkz, rk2; // component of rk-vectors
int nkx = md->nk.x;
int nky = md->nk.y;
int nkz = md->nk.z;
// arrays for keeping iexp(k*r) Re and Im part
float2 el[2];
float2 em[NKVEC_MX];
float2 en[NKVEC_MX];
float2 sums[NTOTKVEC]; // summ (q iexp (k*r)) for each k
extern __shared__ float2 sh_sums[]; // the same in shared memory
float2 lm; // temp var for keeping el*em
float2 ck; // temp var for keeping q * el * em * en (q iexp (kr))
// invert length of box cell
float ra = md->revLeng.x;
float rb = md->revLeng.y;
float rc = md->revLeng.z;
if (threadIdx.x == 0)
for (i = 0; i < md->nKvec; i++)
sh_sums[i] = make_float2(0.0f, 0.0f);
__syncthreads();
for (i = 0; i < md->nKvec; i++)
sums[i] = make_float2(0.0f, 0.0f);
int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
int N = min(id0 + atPerThread, md->nAt);
ik = 0;
for (i = id0; i < N; i++)
{
// save charge
ch = md->specs[md->types[i]].charge;
el[0] = make_float2(1.0f, 0.0f); // .x - real part (or cos) .y - imagine part (or sin)
em[0] = make_float2(1.0f, 0.0f);
en[0] = make_float2(1.0f, 0.0f);
// iexp (ikr)
sincos(d_2pi * md->xyz[i].x * ra, &(el[1].y), &(el[1].x));
sincos(d_2pi * md->xyz[i].y * rb, &(em[1].y), &(em[1].x));
sincos(d_2pi * md->xyz[i].z * rc, &(en[1].y), &(en[1].x));
// fil exp(iky) array by complex multiplication
for (l = 2; l < nky; l++)
{
em[l].x = em[l - 1].x * em[1].x - em[l - 1].y * em[1].y;
em[l].y = em[l - 1].y * em[1].x + em[l - 1].x * em[1].y;
}
// fil exp(ikz) array by complex multiplication
for (l = 2; l < nkz; l++)
{
en[l].x = en[l - 1].x * en[1].x - en[l - 1].y * en[1].y;
en[l].y = en[l - 1].y * en[1].x + en[l - 1].x * en[1].y;
}
// MAIN LOOP OVER K-VECTORS:
for (l = 0; l < nkx; l++)
{
rkx = l * d_2pi * ra;
// move exp(ikx[l]) to ikx[0] for memory saving (ikx[i>1] are not used)
if (l == 1)
el[0] = el[1];
else if (l > 1)
{
// exp(ikx[0]) = exp(ikx[0]) * exp(ikx[1])
tmp = el[0].x;
el[0].x = tmp * el[1].x - el[0].y * el[1].y;
el[0].y = el[0].y * el[1].x + tmp * el[1].y;
}
//ky - loop:
for (m = mmin; m < nky; m++)
{
rky = m * d_2pi * rb;
//set temporary variable lm = e^ikx * e^iky
if (m >= 0)
{
lm.x = el[0].x * em[m].x - el[0].y * em[m].y;
lm.y = el[0].y * em[m].x + em[m].y * el[0].x;
}
else // for negative ky give complex adjustment to positive ky:
{
lm.x = el[0].x * em[-m].x + el[0].y * em[-m].y;
lm.y = el[0].y * em[-m].x - em[-m].x * el[0].x;
}
//kz - loop:
for (n = nmin; n < nkz; n++)
{
rkz = n * d_2pi * rc;
rk2 = rkx * rkx + rky * rky + rkz * rkz;
if (rk2 < md->rKcut2) // cutoff
{
// calculate summ[q iexp(kr)] (local part)
if (n >= 0)
{
ck.x = ch * (lm.x * en[n].x - lm.y * en[n].y);
ck.y = ch * (lm.y * en[n].x + lm.x * en[n].y);
}
else // for negative kz give complex adjustment to positive kz:
{
ck.x = ch * (lm.x * en[-n].x + lm.y * en[-n].y);
ck.y = ch * (lm.y * en[-n].x - lm.x * en[-n].y);
}
sums[ik].x += ck.x;
sums[ik].y += ck.y;
// save qiexp(kr) for each k for each atom:
md->qiexp[i][ik] = ck;
ik++;
}
} // end n-loop (over kz-vectors)
nmin = 1 - nkz;
} // end m-loop (over ky-vectors)
mmin = 1 - nky;
} // end l-loop (over kx-vectors)
} // end loop by atoms
// save sum into shared memory
for (i = 0; i < md->nKvec; i++)
{
atomicAdd(&(sh_sums[i].x), sums[i].x);
atomicAdd(&(sh_sums[i].y), sums[i].y);
}
__syncthreads();
//...and to global
int step = ceil((double)md->nKvec / (double)blockDim.x);
id0 = threadIdx.x * step;
N = min(id0 + step, md->nKvec);
for (i = id0; i < N; i++)
{
atomicAdd(&(md->qDens[i].x), sh_sums[i].x);
atomicAdd(&(md->qDens[i].y), sh_sums[i].y);
}
}
// end 'ewald_rec' function
__global__ void ewald_force(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the second part : enegy and forces
{
int i; // for atom loop
int ik; // index of k-vector
float tmp;
// accumulator for force components
float3 force;
// constant factors for energy and force
float eScale = md->ewEscale;
float fScale = md->ewFscale;
int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
int N = min(id0 + atPerThread, md->nAt);
for (i = id0; i < N; i++)
{
force = make_float3(0.0f, 0.0f, 0.0f);
// summ by k-vectors
for (ik = 0; ik < md->nKvec; ik++)
{
tmp = fScale * md->exprk2[ik] * (md->qiexp[i][ik].y * md->qDens[ik].x - md->qiexp[i][ik].x * md->qDens[ik].y);
force.x += tmp * md->rk[ik].x;
force.y += tmp * md->rk[ik].y;
force.z += tmp * md->rk[ik].z;
}
md->frs[i].x += force.x;
md->frs[i].y += force.y;
md->frs[i].z += force.z;
} // end loop by atoms
// one block calculate energy
if (blockIdx.x == 0)
if (threadIdx.x == 0)
{
for (ik = 0; ik < md->nKvec; ik++)
md->engCoul2 += eScale * md->exprk2[ik] * (md->qDens[ik].x * md->qDens[ik].x + md->qDens[ik].y * md->qDens[ik].y);
}
}
// end 'ewald_force' function
Espero que você me perdoe por deixar comentários em inglês, o código é praticamente o mesmo da versão serial. O código ficou ainda mais legível devido ao fato de as matrizes perderem uma dimensão: elc / s [i] [l] , emc / s [i] [m] e enc / s [i] [n] transformadas em unidimensional el , em e br , matrizes LMC / s e CKC / s - para as variáveis lm e ck (dimensão de partículas desapareceu, uma vez que já não há a necessidade de armazenar para cada partícula, o resultado intermédio é acumulado na memória partilhada). Infelizmente, surgiu um problema imediatamente: as matrizes em e enteve que ser definido como estático para não usar a memória global e não alocar memória dinamicamente a cada vez. O número de elementos neles é determinado pela diretiva NKVEC_MX (o número máximo de vetores k em uma dimensão) no estágio de compilação, e apenas os primeiros elementos nky / z são usados em tempo de execução. Além disso, apareceu um índice de ponta a ponta em todos os vetores k e uma diretiva semelhante, limitando o número total desses vetores NTOTKVEC . O problema surgirá se o usuário precisar de mais vetores k do que o especificado pelas diretivas. Para calcular a energia, é fornecido um bloco com índice zero, pois não importa qual bloco executará esse cálculo e em que ordem. Observe que o valor calculado na variável akko código serial depende apenas do tamanho do sistema simulado e pode ser calculado no estágio de inicialização. Na minha implementação, ele é armazenado na matriz md-> exprk2 [] para cada vetor-k. Da mesma forma, os componentes dos vetores k são retirados da matriz md-> rk [] . Aqui, pode ser necessário usar funções FFT prontas, já que o método é baseado nele, mas eu ainda não descobri como fazê-lo.
Bem, agora vamos tentar contar algo, mas o mesmo cloreto de sódio. Vamos pegar 2 mil íons de sódio e a mesma quantidade de cloro. Vamos definir as cobranças como números inteiros e tirar potenciais de pares, por exemplo, deste trabalho. Vamos definir a configuração inicial aleatoriamente e misturá-la levemente, Figura 2a. Escolhemos o volume do sistema para que ele corresponda à densidade do cloreto de sódio à temperatura ambiente (2,165 g / cm 3 ). Vamos começar tudo isso por um curto período de tempo (10.000 etapas de 5 femtossegundos) com consideração ingênua da eletrostática de acordo com a lei de Coulomb e usando o somatório de Ewald. As configurações resultantes são mostradas nas Figuras 2b e 2c, respectivamente. Parece que, no caso de Ewald, o sistema é um pouco mais simplificado do que sem ele. Também é importante que as flutuações totais de energia tenham diminuído significativamente com o uso da soma.

Figura 2. Configuração inicial do sistema NaCl (a) e após 10.000 etapas de integração: método ingênuo (b) e com o esquema de Ewald (c).
Em vez de uma conclusão
Observe que a estrutura obtida na figura não corresponde à estrutura cristalina NaCl, mas sim à estrutura ZnS, mas isso já é uma reclamação sobre potenciais de pares. Levar em consideração a eletrostática é muito importante para a modelagem da dinâmica molecular. Acredita-se que a interação eletrostática seja responsável pela formação das redes cristalinas, uma vez que atua a grandes distâncias. É verdade que desta posição é difícil explicar como substâncias como o argônio se cristalizam durante o resfriamento.
Além do método de Ewald mencionado, também existem outros métodos de contabilização de eletrostática, veja, por exemplo, esta revisão .