
A otimização nos negócios na esmagadora maioria dos casos está associada ao uso do método de programação linear. O método é bastante simples. Além disso, existe um teorema sobre a existência e a exclusividade da solução.
No entanto, na prática, tudo não é totalmente simples.
O primeiro problema é a não linearidade das condições do mundo real. Para que o método de programação linear seja aplicável, eles devem ser linearizados. Existem maneiras de definir de maneira plausível a não linearidade através de equações lineares e desigualdades, introduzindo novas variáveis, definindo coeficientes de peso, etc. Ao resolver problemas de produção, neste caso, é necessário operar com um grande número de variáveis e, consequentemente, equações (desigualdades).
Na teoria da resolução de problemas extremos, existe um teorema sobre a estabilidade de soluções para problemas de programação linear. Segundo ele, a solução é estável apenas se o domínio do problema for convexo. Com um grande número de variáveis e desigualdades, não é possível estabelecer se o domínio do problema é convexo. Além disso, a probabilidade de não-convexidade é alta.
Se o problema não for estável, dependendo do ponto de partida da travessia dos vértices, resultados diferentes serão obtidos.
Segundo problema- restrição da variável de baixo (x> h> 0). Qualquer implementação de um método de programação linear sempre fornecerá um valor x diferente de zero. Se x for exatamente igual a h, isso significa que o valor da variável x deve ser essencialmente zero. Na prática, esses volumes "fictícios" (método de curtose) estão espalhados por variáveis "significativas". A conseqüência dessa prática é a erosão do conceito de solução ideal, o que é especialmente importante se essa solução for uma das muitas na cadeia de decisão.
O terceiro problema é gerencial. O método de programação linear fornece apenas um resultado. E como olhar para os resultados próximos do ideal? Por exemplo, na solução resultante, a classificação do fornecedor é baixa. Como entender se existem soluções próximas, mas para fornecedores confiáveis.
Tarefa de transporte
O exemplo corresponde a um problema de programação linear de transporte.
Existem 5 transportadoras (a tarefa foi definida para o transporte de carvão), que possui dois cálculos tarifários. Os limites das tarifas e as próprias tarifas podem ser alteradas (elas são definidas parametricamente).

O transporte é especificado como ponto a ponto (de acordo com o método aceito para transporte de carvão) e volume.
Visão geral da interface.

Área de atribuição de transporte.
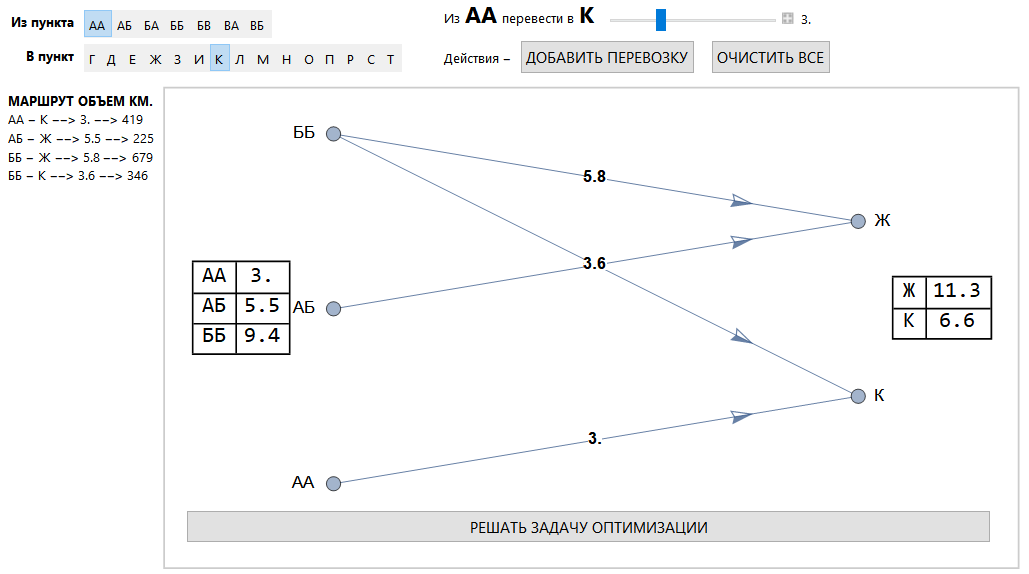
Método de solução de cluster
Em vez de um problema de programação linear, um conjunto de problemas é resolvido, cujo número corresponde a todas as combinações possíveis de tarifas. No envio acima, existem 127 deles (segundo valor no retângulo superior esquerdo).

As soluções ideais são selecionadas do conjunto dos problemas corretos restantes. Cada tarefa fornece uma solução ideal para uma combinação específica de tarifas. As soluções apresentadas acima constituem um certo intervalo de máximos.
Por que o método de cluster é bom:
- existe um entendimento da estabilidade da solução.
- não há volumes “fictícios” para variáveis delimitadas abaixo, pois haverá outra combinação em que essa condição está ausente (uma vez que essa variável está ausente).
- condições subjetivas (classificações, preferências) podem ser introduzidas usando o método de programação linear padrão.
Com um número maior de remessas, temos a seguinte imagem (fragmento).
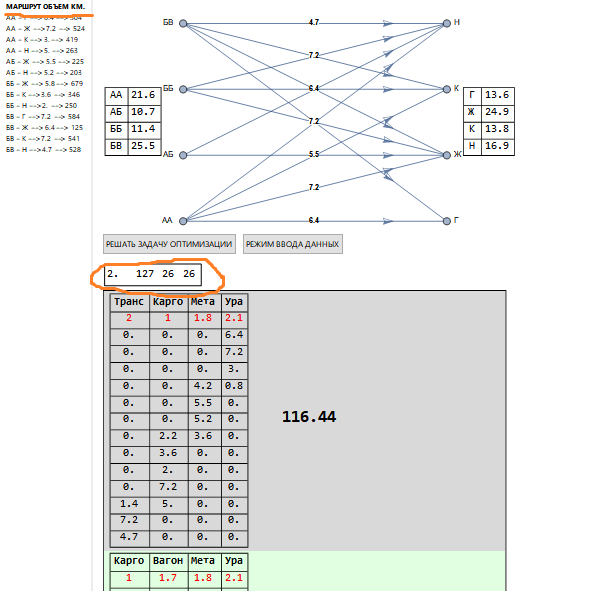
No canto superior esquerdo do retângulo acima das soluções (destacadas em laranja), outros valores são indicados que antes: 127 - combinações (como antes, que está relacionada à estrutura das escalas tarifárias), 26 - corresponde ao número de problemas corretos que estão sendo resolvidos. A tarifa utilizada é indicada em vermelho sob o nome da transportadora e as colunas de transporte correspondem à lista de rotas (sublinhada em laranja).
É importante observar que o método usado permite entender o resultado, avaliar soluções semelhantes e usar sua experiência profissional ao escolher alternativas, levando em consideração os meandros da administração de um negócio específico.