Joshua Green e Andrew Lobb, entediados em quarentena, descobriram como provar uma das variantes do teorema do peg retangular

Todos os tipos de retângulos podem ser encontrados em um circuito fechado?
Em meados de março, os matemáticos Joshua Green e Andrew Lobb se encontraram em uma posição semelhante - trancados em quatro paredes, tentando se adaptar à crescente epidemia de coronavírus. Eles decidiram lidar com isso investigando suas pesquisas.
"Acho que a pandemia foi algum tipo de catalisador para esse processo", disse Greene, professor do Boston College. "Decidimos que seria melhor realizar algum tipo de trabalho conjunto que possa nos apoiar".
Um dos problemas que os dois amigos decidiram enfrentar foi uma variante da questão geométrica que permaneceu sem resposta por mais de cem anos.
"Essa tarefa é extremamente simples de formular e entender, mas é muito difícil de resolver" - disseElizabeth Denn de Washington e Lee University.
Tudo começa com um loop fechado - qualquer caminho curvo que tenha o mesmo começo e fim. A tarefa que Green e Lobb assumiram essencialmente argumenta que, em qualquer caminho desse tipo, existem conjuntos de quatro pontos que compõem os vértices de um retângulo de qualquer proporção.
E, embora esse "problema com pinos retangulares" pareça uma pergunta que qualquer aluno do ensino médio com uma régua e uma bússola pode lidar, ele resistiu às tentativas mais persistentes dos matemáticos por muitas décadas. E quando Green e Lobb assumiram, eles não tinham motivos para esperar mais nada.
Greene disse que, de todos os projetos difíceis em que trabalhou, "este foi o menos promissor na minha opinião".
Mas a pandemia cresceu, e Green e Lobb, que trabalham na Universidade de Durham, na Inglaterra, e no Instituto de Ciência e Tecnologia de Okinawa, respectivamente, tiveram conversas semanais sobre o Zoom e rapidamente geraram várias idéias. E então, em 19 de maio, quando muitas partes do mundo reabriram, eles publicaram sua decisão .
Sua prova final, que mostra que os retângulos podem realmente ser encontrados, leva esse problema a um nível geométrico completamente diferente. E aí esta pergunta teimosa cede com muita facilidade.
"É muito estranho", disse Richard Schwartz, da Brown University. "Essa ideia foi perfeita para esta tarefa."
Repensando retângulos
O problema dos pinos retangulares está intimamente relacionado à questão colocada pelo matemático alemão Otto Töplitz em 1911. Ele previu que em qualquer curva fechada você pode encontrar quatro pontos, conectando os quais você pode obter um quadrado. Essa questão dele sobre "pinos quadrados" permanece em aberto.
"Esta é uma tarefa antiga e frustrante que não pode ser invadida de forma alguma", disse Green.
Para entender a complexidade do problema, é importante conhecer as propriedades das curvas consideradas no problema do peg quadrado - isso também é importante para a prova de Green e Lobb.
Este casal resolveu o problema das curvas fechadas, "contínuas" e "suaves". Continuidade significa sem interrupções. Suavidade significa continuidade e sem cantos. É provável que você desenhe uma curva suave e contínua se sentar à mesa com papel e lápis. Eles são "mais fáceis de trabalhar", disse Green.
As curvas contínuas suaves são diferentes das curvas simplesmente contínuas, mas não suaves, como as envolvidas na conjectura de pinos quadrados de Toeplitz. Essa curva pode ter cantos - pontos nos quais a curva se desvia repentinamente e segue em uma direção diferente. Um exemplo primordial de uma curva com muitos ângulos é a curva de Koch fractal semelhante a um floco de neve ., de fato, consistindo em alguns cantos. O floco de neve de Koch e outras curvas semelhantes não podem ser analisadas usando métodos algébricos, o que os torna especialmente difíceis de estudar.
"Algumas curvas contínuas [não suaves] são nojentas", disse Denn.
Ainda assim, o problema resolvido por Green e Lobb pertence a curvas suaves e, portanto, contínuas. E, em vez de descobrir se há sempre quatro pontos nessas curvas que formam um quadrado - para curvas contínuas suaves, esse problema foi resolvido em 1929 - eles estudaram outra coisa: sempre há quatro pontos nessas curvas que formam um retângulo de qualquer dado proporções, ou seja, com qualquer proporção. Para um quadrado, essa proporção é de 1: 1, para TVs de alta definição - 16: 9.

O primeiro grande avanço no problema do peg retangular veio em evidências encontradas no final da década de 1970 por Herbert Vaughn. Ele ofereceu uma nova maneira de olhar a geometria dos retângulos e forneceu vários métodos que foram posteriormente utilizados por outros matemáticos, incluindo Green e Lobb.
"Todo mundo conhece essa prova", disse Green. "É quase folclórico, você aprende sobre essas coisas discutindo tudo na mesa de jantar".
Em vez de imaginar um retângulo como quatro pontos conectados, Vaughn o imaginou como dois pares de pontos em um relacionamento um com o outro.

Imagine um retângulo com vértices ABCD. Nela, a distância entre os pontos AC (na diagonal) é igual à distância entre os pontos BD (na outra diagonal). Além disso, essas diagonais se cruzam exatamente no meio.
Portanto, ao procurar retângulos em um loop fechado, você pode procurar pares de pontos localizados nas extremidades dos mesmos segmentos de linha que se cruzam no meio. Para encontrá-los, é importante criar uma maneira sistemática de descrevê-los.
Para entender o que isso significa, vamos começar com algo mais simples. Pegue a linha numérica. Vamos escolher dois pontos - digamos os números 7 e 8 - e construí-los como um ponto no plano numérico (7, 8). Também podemos construir pontos que são um par de números idênticos (7, 7). Agora vamos considerar todos os pares possíveis de números que podem ser encontrados na linha numérica (e existem muitos!). Se construirmos todos os pares de tais números, preencheremos todo o plano numérico. Outra maneira de expressar isso é dizer que o plano numérico "parametriza", ou seja, coleta todos os pares de números na linha numérica de maneira ordenada.
Vaughn fez algo semelhante com pares de pontos em uma curva fechada. Como a linha numérica, unidimensional, apenas se fecha sobre si mesma. Ele percebeu que se você pegar pares de pontos com uma curva e construir uma figura a partir deles (e não importa qual é a coordenada x e qual é o y), o avião não funcionará. Em vez disso, você obtém uma figura inesperada - uma tira Mobius , uma superfície bidimensional com apenas um lado.

E, em certo sentido, isso é bastante lógico. Para entender o porquê - selecione um par de pontos na curva e nomeie-os x e y. Agora vá de x para y, movendo-se ao longo de uma parte da curva e simultaneamente - de y para x, movendo-se ao longo do oposto. No processo, você passará por todos os pares de pontos da curva, iniciando e terminando em um par não ordenado (x, y). Mas isso o levará ao começo - apenas a sequência final de pontos será oposta à inicial. Um loop de pontos desordenados que mudam de orientação para o oposto é a essência da faixa de Möbius.
Essa faixa fornece aos matemáticos um novo objeto que pode ser analisado como parte do problema do peg retangular. Vaughn usou esse fato para provar que em qualquer curva há pelo menos um conjunto de quatro pontos que formam um quadrado.
Respostas quadridimensionais
A prova de Green e Lobb é baseada no trabalho de Vaughn. No entanto, também combina várias descobertas adicionais, algumas das quais são relativamente recentes. A prova final é como um instrumento preciso, cujo resultado desejado se baseia em uma combinação de idéias cuidadosamente considerada.
Um dos primeiros ingredientes principais de sua prova veio em novembro de 2019, quando o estudante de doutorado da Universidade de Princeton, Cole Hugelmeyer, publicou o artigodemonstrando uma nova maneira de analisar a faixa de Möbius usada por Vaughn. Ele usou um processo matemático conhecido como aninhamento, que é quando pegamos um objeto e o projetamos no espaço geométrico. Como resultado, Green e Lobb pegaram a técnica de Hugelmeyer e a transferiram para outro espaço geométrico. Mas para entender o que eles fizeram, primeiro você precisa entender o que ele fez.
Aqui está um exemplo simples de aninhamento.
Vamos começar com uma linha unidimensional. Cada ponto de uma linha reta é definido por um único número. Agora vamos incorporar esta linha no espaço bidimensional - isto é, vamos desenhá-la em um plano.
Após incorporar uma linha reta no plano xy, cada ponto já é determinado por dois números - as coordenadas x e y, que descrevem onde exatamente o ponto está no plano. Agora você pode analisar a linha usando técnicas de geometria 2D.
A ideia de Hugelmeier era pegar algo como uma faixa de Möbius, mas incorporá-la em um espaço 4, onde as propriedades da geometria 4-dimensional permitirão que você prove os resultados desejados.
“Basicamente, você tem uma faixa Mobius e precisa atribuir quatro coordenadas a cada ponto. Será algo como o endereço de um ponto no espaço quadridimensional ”, disse Lobb.
Hugelmeyer atribuiu esses endereços de maneira que fosse mais fácil chegar ao objetivo principal, encontrando retângulos em uma curva. Podemos dizer que ele atribuiu a cada ponto da curva algo como um endereço postal - estado, cidade, nome da rua e número da casa.
Para fazer isso, ele partiu de um ponto específico na faixa Mobius e anotou os dois pontos na curva fechada original que ela denotava. Então, ele encontrou o ponto médio do segmento de linha conectando esses pontos e determinou suas coordenadas x e y. Obtivemos os dois primeiros valores do endereço quadridimensional (estado e cidade).
Ele então mediu a distância entre os dois pontos originais na curva. Esse comprimento se tornou o terceiro valor do endereço quadridimensional (nome da rua). Finalmente, ele calculou o ângulo entre o segmento de linha que liga os dois pontos originais e o eixo x. Esse ângulo tornou-se o quarto valor do endereço quadridimensional (número da casa). Esses quatro valores informam tudo sobre um par de pontos na curva.

Este exercício parece bastante desafiador, mas valeu a pena rapidamente. Hugelmeyer pegou a tira Mobius anexada e a virou. A faixa do Mobius girada se moveu em relação à sua posição original e as duas cópias da faixa se cruzam. Desde que a curva ocorreu no espaço quadridimensional, é difícil imaginar a forma de auto-interseção da faixa de Möbius - mas é fácil descrevê-la matematicamente.
Esse cruzamento foi de grande importância. Quando duas cópias da faixa Mobius são sobrepostas, dois pares de pontos podem ser encontrados na curva fechada original, formando os quatro vértices do retângulo.
Por quê?
Primeiro, lembre-se de que um retângulo pode ser representado como dois pares de pontos com um centro comum de interseção de segmentos do mesmo comprimento que os conectam. São essas informações que são codificadas nos três primeiros valores do endereço quadridimensional atribuído a cada ponto da faixa de Möbius aninhada.
Em segundo lugar, no espaço quadridimensional, é possível desdobrar a faixa de Möbius de forma a alterar apenas uma das coordenadas de cada ponto em seu endereço quadridimensional - o número da casa muda, mas a rua, cidade e estado permanecem. Como exemplo, lembre-se de que, se você pegar um tijolo, posicione-o à sua frente e mova-o para a direita; somente sua coordenada x será alterada, mas não y ou z.
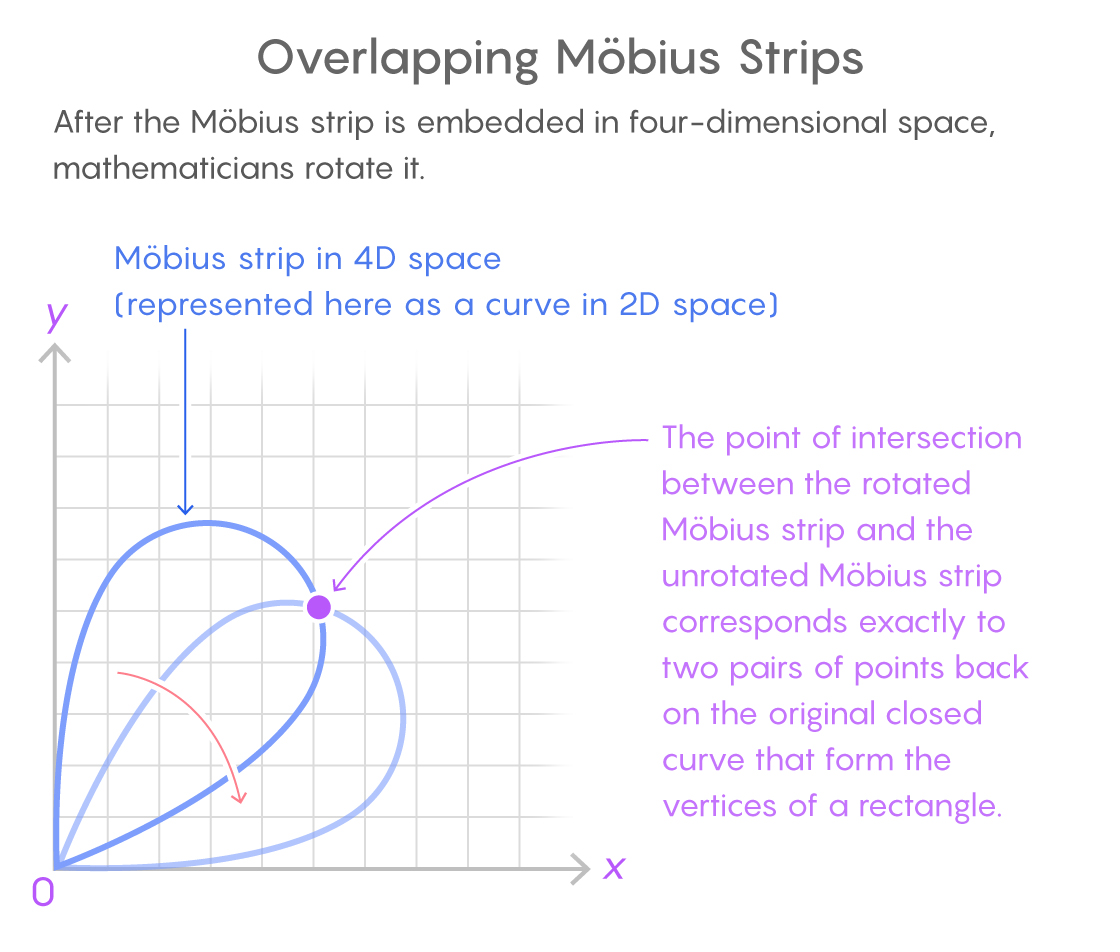
A faixa de Möbius no espaço quadridimensional é aqui indicada por uma curva bidimensional. O ponto de interseção das duas cópias corresponde a dois pares de pontos na curva fechada original que formam um retângulo.
Hugelmeyer explicou como girar a faixa Mobius no espaço quadridimensional, para que as duas coordenadas que indicam o ponto médio das linhas que conectam os pares não mudem - assim como as coordenadas que indicam a distância entre pares de pontos. Sua rotação mudou apenas a última coordenada - contendo informações sobre o ângulo em que o segmento que liga os pontos está localizado.
Como resultado, a interseção da cópia girada da faixa de Möbius e seu original correspondia exatamente a dois pares de pontos localizados em uma curva fechada, tendo um centro comum (interseções dos segmentos que os conectam) e localizados à mesma distância um do outro. Ou seja, essa interseção correspondia aos quatro vértices do retângulo na curva.
A estratégia de usar a interseção de dois espaços para encontrar os pontos certos há muito tempo é usada no trabalho sobre os problemas de estacas quadradas e retangulares.
"No cruzamento desses espaços está o desejado", disse Denn. "Muitas das evidências da história dos pinos quadrados têm essa ideia".
Hugelmeyer usou uma estratégia de interseção em um ambiente quadridimensional e conseguiu mais do que qualquer um antes dele. A tira Mobius pode ser girada em qualquer ângulo de 0 ° a 360 °, e ele provou que um terço de todas essas rotações resulta na interseção do original e da cópia girada. Isso equivale a dizer que você pode encontrar retângulos em uma curva fechada com um terço de todas as proporções possíveis.
"Damos crédito a Cole por pensar em colocar uma faixa Mobius no espaço 4D e usar técnicas 4D", disse Green.
Ao mesmo tempo, o resultado de Hugelmeier acabou sendo provocativo: se o espaço quadridimensional é tão útil para lidar com esse problema, por que ele foi útil para apenas um terço de todos os retângulos?
"Afinal, tem que haver uma maneira de obter os dois terços restantes", disse Green. - Mas como?"
Abordagem simplética
Green e Lobb estavam interessados no problema de estacas retangulares antes mesmo que a pandemia os mandasse para casa. Em fevereiro, Lobb organizou uma conferência no Instituto de Ciência e Tecnologia de Okinawa , da qual Green também participou. O casal passou alguns dias conversando sobre essa tarefa. Depois disso, eles discutiram por mais uma semana, ao longo do caminho vendo as vistas de Tóquio.
"Não paramos de discutir esse assunto", disse Lobb. "Fomos a restaurantes, cafés, museus e, de tempos em tempos, tínhamos pensamentos sobre isso".
Eles continuaram suas discussões mesmo depois de terem sido trancados em suas casas. Eles esperavam provar que qualquer rotação da faixa Mobius daria um ponto de interseção - o que equivale a encontrar retângulos de qualquer proporção.
Em meados de abril, eles formaram uma estratégia. Isso significava incorporar a fita em um tipo especial de espaço quadridimensional. O aninhamento regular implica que você coloque o objeto desejado de qualquer maneira. Imagine quantas maneiras você pode incorporar uma curva fechada unidimensional em um plano bidimensional - o número deles é infinito, pois existem infinitas maneiras pelas quais você pode colocar um fio amarrado em um loop em uma tabela.
Mas digamos que a superfície bidimensional na qual você aninha o loop tenha sua própria estrutura. Imagine, por exemplo, um mapa com setas (ou vetores) indicando em que direção e a que velocidade o vento sopra na superfície da Terra. Agora você tem uma superfície 2D com informações ou estrutura adicionais em cada ponto.
Em seguida, você pode introduzir restrições - uma RFP unidimensional deve ser colocada no mapa para sempre seguir as instruções das setas no mapa.
"Você está limitando as coisas para que a curva siga esses vetores", disse Schwartz. E agora você tem menos maneiras de colocar a curva.

Outros espaços geométricos podem impor restrições diferentes. Importante para o trabalho de Green e Lobb foi o chamado. espaço simplético .
Este conceito geométrico apareceu pela primeira vez no século 19 ao estudar sistemas físicos como planetas em órbita. A posição de um planeta em movimento no espaço tridimensional é determinada por três coordenadas. Mas, como observou o matemático irlandês William Rowan Hamilton, em cada ponto do caminho de movimento do planeta, você também pode colocar um vetor que denota seu momento.
Nos anos 80, o matemático soviético e russo Vladimir Igorevich Arnold desenvolveu o estudo da geometria simplética . Ele percebeu que os espaços geométricos de uma estrutura simplética, quando girados, se cruzam com mais frequência do que os espaços que não possuem essa estrutura.
Isso foi perfeito para Green e Lobb, pois eles queriam resolver o problema do peg retangular para todas as proporções, provando que uma cópia girada de uma faixa Mobius parametrizadora também se cruza com frequência. Então eles começaram a tentar incorporar uma faixa bidimensional de Möbius em um espaço simplético quadridimensional. "Uma idéia radicalmente nova era abordar esse problema do ponto de vista da geometria simplética", disse Green. "E isso mudou tudo."
No final de abril, Green e Lobb determinaram que era possível incorporar uma tira Mobius em um espaço simplético quadridimensional para que ela ficasse alinhada com sua estrutura. Depois disso, eles poderiam começar a usar ferramentas de geometria simplética, muitas das quais estão diretamente relacionadas à questão das auto-interseções.
"Se a faixa de Möbius puder ser feita seguindo regras simpléticas, alguns dos teoremas simpléticos poderão ser usados", disse Lobb.
Green e Lobb estavam confiantes de que poderiam melhorar o resultado de Hugelmeyer - isto é, provar que o cruzamento não ocorre apenas em um terço de todos os cantos. Isso significa que, a partir dos pontos da curva, será possível fazer retângulos com mais de um terço de todas as proporções possíveis.
"Quando tivemos essa ideia, ficou claro que algo iria acontecer", disse Lobb.
No entanto, seus resultados foram mais gerais e pareciam muito mais rápidos do que esperavam. Tudo graças a um objeto matemático estranho - a garrafa de Klein , que no contexto da geometria simplética tem uma propriedade importante.
Conexão de garrafa Klein
A garrafa Klein é uma superfície bidimensional que parece um jarro modernista. Como a tira Mobius, possui apenas uma superfície e pode ser feita colando duas tiras Mobius. Qualquer garrafa de Klein que você possa coletar e colocar em sua mesa (como muitos matemáticos fazem) passa por si mesma. É impossível colocar uma garrafa de Klein no espaço tridimensional para que não se cruze.
"A garrafa Klein precisa ser uma superfície, mas sua alça precisa romper a garrafa para ir de fora para dentro", disse Schwartz.
De qualquer forma, este não é necessariamente o caso. A garrafa Klein pode ser aninhada no espaço 4D para que não se cruze. A quarta dimensão oferece espaço para manobras, e a garrafa Klein pode se desviar. Isso pode ser comparado ao modo como, se duas pessoas caminham uma em direção à outra em uma linha unidimensional, elas não podem evitar uma colisão, mas se andar em um piso bidimensional, elas podem se virar facilmente.

Em maio, Green e Lobb lembraram um fato sobre a garrafa de Klein - ela não pode ser incorporada em um espaço simplético quadridimensional para que não se cruze [a partir do trabalho de outro matemático russo, Vsevolod Viktorovich Shevchishinrelativo à incorporação lagrangiana da garrafa de Klein no espaço quadridimensional / aprox. transl.]. Em outras palavras, não existe uma garrafa de Klein sem auto-interseção que satisfaça todos os requisitos de um espaço simplético. Este fato se tornou a chave da prova. "Era uma varinha mágica", disse Green.
E é por isso. Green e Lobb já demonstraram que é possível incorporar uma tira Mobius em um espaço simplético quadridimensional, para que ele satisfaça seus requisitos. Eles só precisavam descobrir se cada volta da faixa Mobius cruza a cópia original.
No entanto, duas tiras Mobius que se cruzam são equivalentes a uma garrafa de Klein, que se cruza nesse espaço. E se você girar a faixa do Mobius para que a cópia girada não cruze com o original, você obterá uma garrafa de Klein que não se cruza. Mas tal garrafa de Klein não pode existir no espaço simplético quadridimensional. Portanto, qualquer rotação possível da faixa de Möbius aninhada também deve se cruzar - ou seja, em cada curva suave fechada, quatro pontos podem ser encontrados que formam um retângulo de qualquer proporção.
O fim da prova atinge o leitor como uma avalanche.
"É a primeira instalação, instalação e, depois, o grunhido, e a prova está pronta", disse Denn.
A prova de Green e Lobb é um bom exemplo de como resolver um problema geralmente depende de encontrar o ponto de vista correto. Gerações de matemáticos não conseguiram lidar com esta versão do problema do pino retangular, porque tentaram resolvê-lo em condições geométricas mais tradicionais. Quando Green e Lobb trouxeram o problema para o mundo simplético, ele foi facilmente resolvido.
"Esses problemas, que surgiram nas décadas de 1910 e 1920, não tinham uma plataforma adequada para pensar sobre eles", disse Green. "E agora estamos começando a entender que elas são, de fato, encarnações ocultas do fenômeno da simplicidade".