Detecção de colisão e teorema do eixo divisor

Atualmente, os computadores são computadores poderosos

capazes de executar milhões de operações por segundo. E, naturalmente, você não pode prescindir da simulação do mundo real ou do jogo. Um dos problemas da modelagem e simulação por computador é determinar a colisão de dois objetos, uma das soluções realizada pelo teorema no eixo de separação.







Nota. O artigo dará um exemplo com 2 paralelepípedos (a seguir - cubos), mas a idéia para outros objetos convexos será preservada.

Nota. Toda a implementação será feita no Unity.

Ato 0. Teoria geral

Primeiro, você precisa se familiarizar com o " teorema do hiperplano de separação ", que será a base do algoritmo.



Teorema. Duas geometrias convexas não se cruzam se e somente se houver um hiperplano entre elas que as separa. O eixo ortogonal ao

hiperplano divisor é chamado de eixo divisor e as projeções das figuras nele não se cruzam.





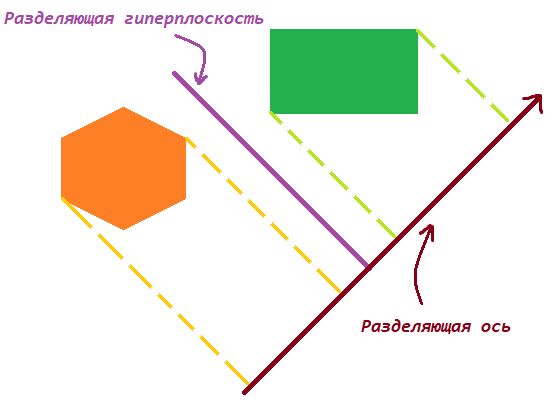
Eixo divisor (caso 2D)





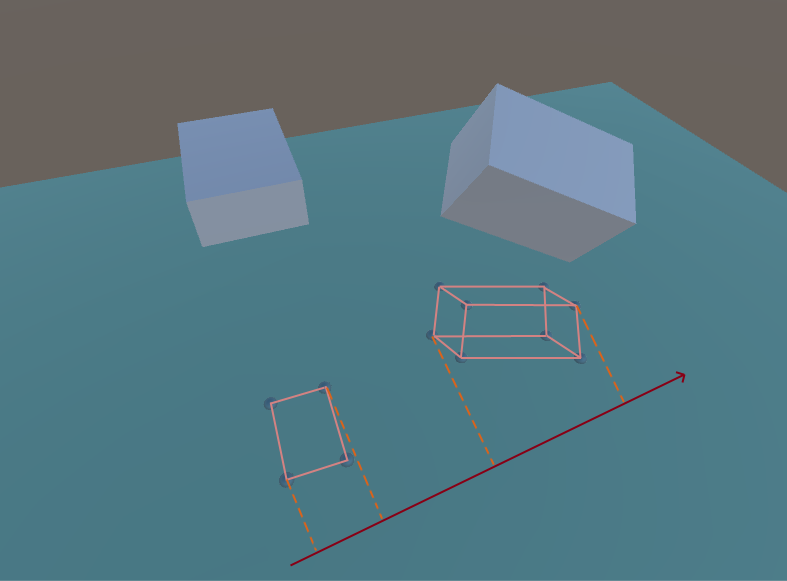
Eixo

divisor (caso 3D) Você pode notar que as projeções no eixo divisor não se cruzam.



Propriedade. O eixo de divisão em potencial estará nos seguintes conjuntos:

• Normas de plano de cada cubo (vermelho)
• Produto vetorial das bordas dos cubos $$$\{[\vec{x},\vec{y}] : x∈X, y∈Y\}$ ,

   onde X é as arestas do primeiro cubo (verde) e Y é o segundo (azul).







Podemos descrever cada cubo com os seguintes dados de entrada:

• Coordenadas do centro do cubo
• Dimensões do cubo (altura, largura, profundidade)
• Quaternion do cubo

Vamos criar uma classe adicional para isso, cujas instâncias fornecerão informações sobre o cubo.

public class Box
{
    public Vector3 Center;
    public Vector3 Size;
    public Quaternion Quaternion;

    public Box(Vector3 center, Vector3 size, Quaternion quaternion)
    {
       this.Center = center;
       this.Size = size;
       this.Quaternion = quaternion;
    }
    //  , 
    //      GameObject
    public Box(GameObject obj)
    {
        Center = obj.transform.position;
        Size = obj.transform.lossyScale;
        Quaternion = obj.transform.rotation;
    }

}

Ato 1. Quaternions

Como costuma ser o caso, um objeto pode girar no espaço. Para encontrar as coordenadas dos vértices, levando em consideração a rotação do cubo, você precisa entender o que é um quaternion.



Quaternion é um número hipercomplexo que determina a rotação de um objeto no espaço.

$$

$$w+xi+yj+zk$$

A parte imaginária (x, y, z) representa um vetor que define a direção da rotação.A

parte real (w) define o ângulo em que a rotação será realizada.



Sua principal diferença em relação a todos os ângulos de Euler usuais é que basta ter um vetor, que determinará a direção da rotação, do que três vetores linearmente independentes que rotacionam o objeto em três subespaços.



Eu recomendo dois artigos que detalham mais os quaterniões:



Um

Dois



Agora que temos um entendimento mínimo sobre quaterniões, vamos entender como girar um vetor e descrever a função de girar um vetor com um quaternion.



Fórmula de rotação vetorial

$$

$$\vec{v}' = q * \vec{v} * \overline{q}$$

$$é o vetor requerido$\vec{v}'$

$$ é o vetor original$\vec{v}$

$$ - quaternion$q$

$$ - quaternion inversa Para começar, vamos dar o conceito de um quaternion inversa em uma base ortonormal - é um quaternion com o sinal oposto da parte imaginária.$\overline{q}$







$$$q = w+xi+yj+zk$

$$ Calcule$\overline{q} = w-xi-yj-zk$



$$$\vec{v} * \overline{q}$



$$$M = \vec{v}*\overline{q} = (0 + v_xi + v_yj + v_zk)(q_w - q_xi - q_yj - q_zk) =$

$$$=\color{red}{v_xq_wi} + \color{purple}{v_xq_x} - \color{blue}{v_xq_yk} + \color{green}{v_xq_zj} +$

$$$+\color{green}{v_yq_wj} + \color{blue}{v_yq_xk} + \color{purple}{v_yq_y} - \color{red}{v_yq_zi} +$

$$$+\color{blue}{v_zq_wk} - \color{green}{v_zq_xj} + \color{red}{v_zq_yi} + \color{purple}{v_zq_z}$



Agora escreveremos os componentes individuais e, a partir deste produto, coletaremos um novo quaternion

$$$M = u_w+u_xi+u_yj+u_zk$

$$$u_w = \color{purple}{v_xq_x + v_yq_y + v_zq_z}$

$$$u_xi = \color{red}{(v_xq_w - v_yq_z + v_zq_y)i}$

$$$u_yj = \color{green}{(v_xq_z + v_yq_w - v_zq_x)j}$

$$$u_zk = \color{blue}{(-v_xq_y + v_yq_x + v_zq_w)k}$



Vamos contar o resto, ou seja, $$$q*M$e obtenha o vetor desejado.



Nota. Para não sobrecarregar os cálculos, apresentamos apenas a parte imaginária (vetorial) deste produto. Afinal, é ela quem caracteriza o vetor desejado.



$$$\vec{v}' = q*M = (q_w + q_xi + q_yj + q_zk)(u_w + u_xi + u_yj + u_zk) =$

$$$= \color{red}{q_wu_xi} + \color{green}{q_wu_yj} + \color{blue}{q_wu_zk} +$

$$$+\color{red}{q_xu_wi} + \color{blue}{q_xu_yk} - \color{green}{q_xu_zj} +$

$$$+\color{green}{q_yu_wj} - \color{blue}{q_yu_xk} + \color{red}{q_yu_zi} +$

$$$+\color{blue}{q_zu_wk} +\color{green}{q_zu_xj} -\color{red}{q_zu_yi}$



Vamos coletar os componentes do vetor



$$$v_x' = \color{red}{q_wu_x + q_xu_w + q_yu_z - q_zu_y}$

$$$v_y' = \color{green}{q_wu_y - q_xu_z + q_yu_w + q_zu_x}$

$$$v_z' = \color{blue}{q_wu_z + q_xu_y - q_yu_x + q_zu_w}$



$$$v' = (v_x', v_y', v_z')$

Assim, o vetor necessário é obtido.Escreva o



código:

private static Vector3 QuanRotation(Vector3 v,Quaternion q)
{
        float u0 = v.x * q.x + v.y * q.y + v.z * q.z;
        float u1 = v.x * q.w - v.y * q.z + v.z * q.y;
        float u2 = v.x * q.z + v.y * q.w - v.z * q.x;
        float u3 = -v.x * q.y + v.y * q.x + v.z * q.w;
        Quaternion M = new Quaternion(u1,u2,u3,u0);
        
        Vector3 resultVector;
        resultVector.x = q.w * M.x + q.x * M.w + q.y * M.z - q.z * M.y;  
        resultVector.y = q.w * M.y - q.x * M.z + q.y * M.w + q.z * M.x;
        resultVector.z = q.w * M.z + q.x * M.y - q.y * M.x + q.z * M.w;
        
        return resultVector;
}

Ato 2. Encontrando os vértices de um cubo

Sabendo como girar um vetor com um quaternion, não será difícil encontrar todos os vértices do cubo.



Vamos passar à função de encontrar os vértices de um cubo. Vamos definir as variáveis ​​básicas.

private static Vector3[] GetPoint(Box box)
{
        //    
        Vector3[] point = new Vector3[8];

        // 
        //....

        return point;
}

Em seguida, você precisa encontrar um ponto (ponto de ancoragem) a partir do qual será mais fácil encontrar outros vértices.



Subtraia metade da dimensão do cubo do centro em sentido de coordenada e adicione uma dimensão do cubo ao ponto de articulação.

//...
        //  
        point[0] = box.Center - box.Size/2;
        point[1] = point[0] + new Vector3(box.Size.x , 0, 0);
        point[2] = point[0] + new Vector3(0, box.Size.y, 0);
        point[3] = point[0] + new Vector3(0, 0, box.Size.z);
		
	//     
        point[4] = box.Center + box.Size / 2;
        point[5] = point[4] - new Vector3(box.Size.x, 0, 0);
        point[6] = point[4] - new Vector3(0, box.Size.y, 0);
        point[7] = point[4] - new Vector3(0, 0, box.Size.z);
//...

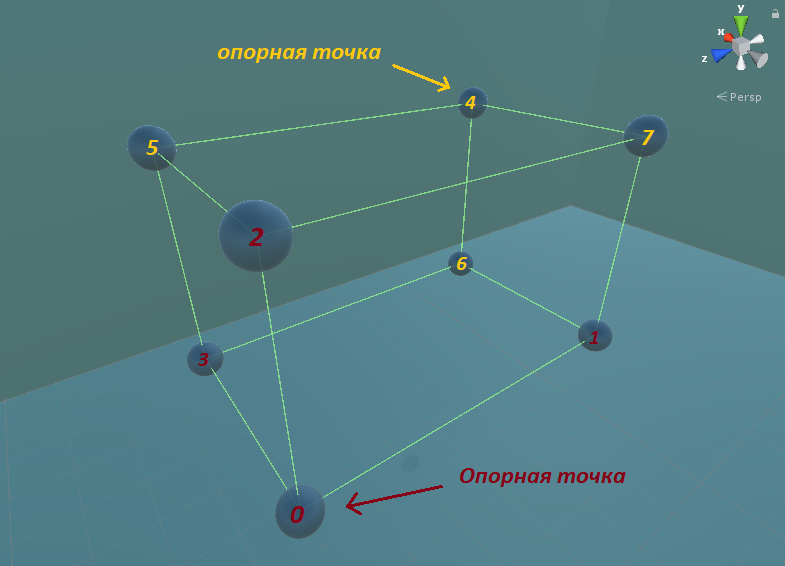
Podemos ver como os pontos são formados.



Após encontrar as coordenadas dos vértices, é necessário rotacionar cada vetor pelo quaternário correspondente.

//...

        for (int i = 0; i < 8; i++)
        {
            point[i] -= box.Center;//    

            point[i] = QuanRotation(point[i], box.Quaternion);//

            point[i] += box.Center;// 
        }

//...

Vamos para as projeções.

Ato 3. Procure eixos divisores

O próximo passo é encontrar o conjunto de eixos que afirmam estar se dividindo.

Lembre-se de que ele pode ser encontrado nos seguintes conjuntos:

• Normais normais de cada cubo (vermelho)
• Produto vetorial das bordas dos cubos $$$\{[\vec{x},\vec{y}[ : x∈X, y∈Y\}$onde X é as arestas do primeiro cubo (verde) e Y é o segundo (azul).

Para obter os eixos necessários, basta ter quatro vértices do cubo, que formam um sistema ortogonal de vetores. Esses vértices estão nas quatro primeiras células da matriz de pontos que formamos no segundo ato.







É necessário encontrar as normais de plano geradas pelos vetores:

• $$$\vec{a}$ e $$$\vec{b}$
• $$$\vec{b}$ e $$$\vec{c}$
• $$$\vec{a}$ e $$$\vec{c}$

Para fazer isso, é necessário percorrer os pares de arestas do cubo para que cada nova amostra forme um plano ortogonal a todos os planos obtidos anteriormente. Foi incrivelmente difícil para mim explicar como funciona, por isso forneci duas versões do código para ajudá-lo a entender.





Mas você pode facilitar:

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //
        Vector3 A;
        Vector3 B;

	//  
        List<Vector3> Axis = new List<Vector3>();

	//   
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            B = a[(i+1)%3+1] - a[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }
	//  
        for (int i = 1; i < 4; i++)
        {
            A = b[i] - b[0];
            B = b[(i+1)%3+1] - b[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }

        //...
}

Também temos que encontrar todos os produtos vetoriais das bordas dos cubos. Isso pode ser organizado por uma pesquisa simples:

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //...
        // 
        //... 

       //    
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            for (int j = 1; j < 4; j++)
            {
                B = b[j] - b[0];
                if (Vector3.Cross(A,B).magnitude != 0)
                {
                    Axis.Add(Vector3.Cross(A,B).normalized);
                }
            }
        }
        return Axis;
}

Ato 4. Projeções no eixo

Chegamos ao ponto mais importante. Aqui temos que encontrar as projeções dos cubos em todos os eixos divisores em potencial. O teorema tem uma consequência importante: se os objetos se cruzam, o eixo no qual a interseção da projeção dos cubos é mínima é a direção (normal) da colisão, e o comprimento do segmento de interseção é a profundidade da penetração.



Mas primeiro, lembre-se da fórmula para a projeção escalar do vetor v no vetor unitário a :

$$

$$proj_\left\langle \vec{a} \right\rangle \vec{v} = \frac{(\vec{v},\vec{a})}{| \vec{a} |}$$

private static float ProjVector3(Vector3 v, Vector3 a)
{
        a = a.normalized;
        return Vector3.Dot(v, a) / a.magnitude;
        
}

Agora descreveremos uma função que determinará a interseção das projeções nos eixos candidatos.



A entrada são os vértices de dois cubos e uma lista de possíveis eixos divisores:

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
           //     
           //         
        }
        //       ,   ,    
        //    .
}

A projeção no eixo é definida por dois pontos que possuem valores máximo e mínimo no próprio eixo:







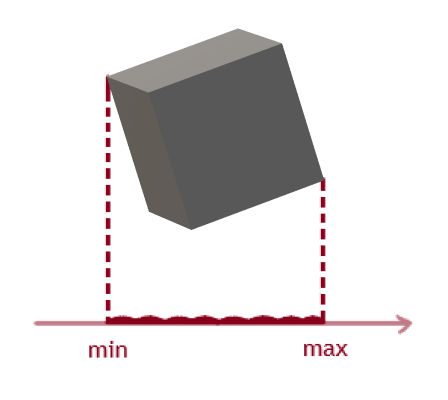
Em seguida, criamos uma função que retorna os pontos de projeção de cada cubo. São necessários dois parâmetros de retorno, uma matriz de vértices e um potencial eixo de divisão.

private static void ProjAxis(out float min, out float max, Vector3[] points, Vector3 Axis)
{
        max = ProjVector3(points[0], Axis);
        min = ProjVector3(points[0], Axis);
        for (int i = 1; i < points.Length; i++)
        {
            float tmp = ProjVector3(points[i], Axis);
            if (tmp > max)
            {
                max = tmp;
            }

            if (tmp < min)
            {
                min= tmp;
            }
        }
}

Então, aplicando esta função ( ProjAxis ), obtemos os pontos de projeção de cada cubo.

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
            //  a
            float max_a;
            float min_a;
            ProjAxis(out min_a,out max_a,a,Axis[j]);

            //  b
            float max_b;
            float min_b;
            ProjAxis(out min_b,out max_b,b,Axis[j]);
            
            //...
        }
        //...
}

Em seguida, com base nos vértices da projeção, determinamos a interseção das projeções:







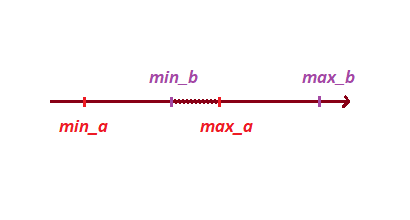
para fazer isso, vamos colocar nossos pontos em uma matriz e classificá-la, esse método nos ajudará a determinar não apenas a interseção, mas também a profundidade da interseção.

            float[] points = {min_a, max_a, min_b, max_b};
            Array.Sort(points);

Observe a seguinte propriedade:



1) Se os segmentos não se cruzarem , a soma dos segmentos será menor que o segmento pelos pontos extremos formados:







2) Se os segmentos se cruzarem , a soma dos segmentos será maior que o segmento pelos pontos extremos formados:







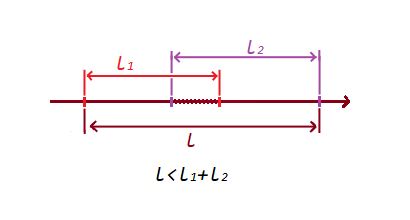
Com uma condição tão simples, verificamos a interseção e a não interseção segmentos.



Se não houver interseção, a profundidade da interseção será zero:

            //...
            // 
            float sum = (max_b - min_b) + (max_a - min_a);
            //  
            float len = Math.Abs(p[3] - p[0]);
            
            if (sum <= len)
            {
                //  
                //  
                return Vector3.zero;
            }
            //,        
            //....

Assim, é suficiente termos pelo menos um vetor no qual as projeções dos cubos não se cruzam, e os próprios cubos não se cruzam. Portanto, quando encontramos o eixo divisor, podemos pular os vetores restantes e finalizar o algoritmo.



No caso de interseção de cubos, tudo é um pouco mais interessante: a projeção dos cubos em todos os vetores se cruzará, e devemos definir o vetor com a interseção mínima.



Vamos criar esse vetor antes do loop e armazenaremos o vetor com o comprimento mínimo. Assim, no final do ciclo, obtemos o vetor desejado.

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        Vector3 norm = new Vector3(10000,10000,10000);
        for (int j = 0; j < Axis.Count; j++)
        {
                //...
        }
        // ,      ,  
        return norm;
{

E toda vez que encontramos o eixo no qual as projeções se cruzam, verificamos se o menor é o comprimento entre todos. multiplicamos esse eixo pelo comprimento da interseção e o resultado será a normal desejada (direção) da interseção dos cubos.



Também adicionei uma definição da orientação do normal em relação ao primeiro cubo.

//...
if (sum <= len)
{
   //  
   //   
   return new Vector3(0,0,0);
}
//,        

//  -    2  1    
//(.       )
float dl = Math.Abs(points[2] - points[1]);
if (dl < norm.magnitude)
{
   norm = Axis[j] * dl;
   // 
   if(points[0] != min_a)
   norm = -norm;
}
//...

Conclusão

O projeto com implementação e exemplo é carregado no GitHub e você pode vê-lo aqui .



Meu objetivo era compartilhar minha experiência na solução de problemas relacionados à determinação das interseções de dois objetos convexos. E também é acessível e compreensível falar sobre esse teorema.