No final do artigo, compartilharemos com você uma lista dos materiais mais interessantes sobre esse tópico.

Nova abordagem
A aprendizagem por reforço multiagente é uma área crescente e rica de pesquisa. No entanto, o uso constante de algoritmos de agente único em contextos multiagentes nos coloca em uma posição difícil. O aprendizado é complicado por vários motivos, principalmente por causa de:
- Não estacionariedade entre agentes independentes;
- Crescimento exponencial de espaços de ações e estados.
Os pesquisadores descobriram muitas maneiras de reduzir o impacto desses fatores. A maioria desses métodos se enquadra no conceito de "planejamento central com execução descentralizada".
Planejamento centralizado
Cada agente tem acesso direto às observações locais. Essas observações podem ser muito diversas: imagens do ambiente, posição em relação a determinados pontos de referência ou até posição em relação a outros agentes. Além disso, durante o treinamento, todos os agentes são controlados por uma unidade ou crítico central.
Embora cada agente possua apenas informações locais e políticas locais para treinamento, existe uma entidade que monitora todo o sistema de agentes e diz a eles como atualizar políticas. Assim, o efeito da não estacionariedade é reduzido. Todos os agentes são treinados usando o módulo com informações globais.
Execução descentralizada
Durante o teste, o módulo central é removido, mas os agentes com suas políticas e dados locais permanecem. Isso reduz os danos causados pelo aumento dos espaços de ações e estados, uma vez que políticas agregadas nunca são estudadas. Em vez disso, esperamos que o módulo central tenha informações suficientes para gerenciar a política de aprendizado local de forma que seja ideal para todo o sistema assim que chegar a hora de realizar os testes.
OpenAI
Pesquisadores da OpenAI, da Universidade da Califórnia em Berkeley e da Universidade McGill, introduziram uma nova abordagem para configurações de vários agentes usando o Gradiente de política determinística profunda de vários agentes . Essa abordagem, inspirada no seu homólogo de agente único, DDPG, usa treinamento de ator para crítico e mostrou resultados muito promissores.
Arquitetura
Este artigo pressupõe que você esteja familiarizado com a versão de agente único do MADDPG: Deep Deterministic Policy Gradients ou DDPG. Para refrescar sua memória, você pode ler o maravilhoso artigo de Chris Yoon .
Cada agente possui um espaço de observação e um espaço de ação contínua. Cada agente também possui três componentes:
- , ;
- ;
- , - Q-.
Enquanto o crítico examina os valores Q conjuntos de uma função ao longo do tempo, ele envia aproximações apropriadas dos valores Q ao ator para ajudar no aprendizado. Na próxima seção, examinaremos essa interação com mais detalhes.
Lembre-se de que o crítico pode ser uma rede compartilhada entre todos os N agentes. Em outras palavras, em vez de treinar N redes que avaliam o mesmo valor, apenas treine uma rede e use-a para ajudar a treinar todos os outros agentes. O mesmo vale para redes de atores se os agentes forem homogêneos.
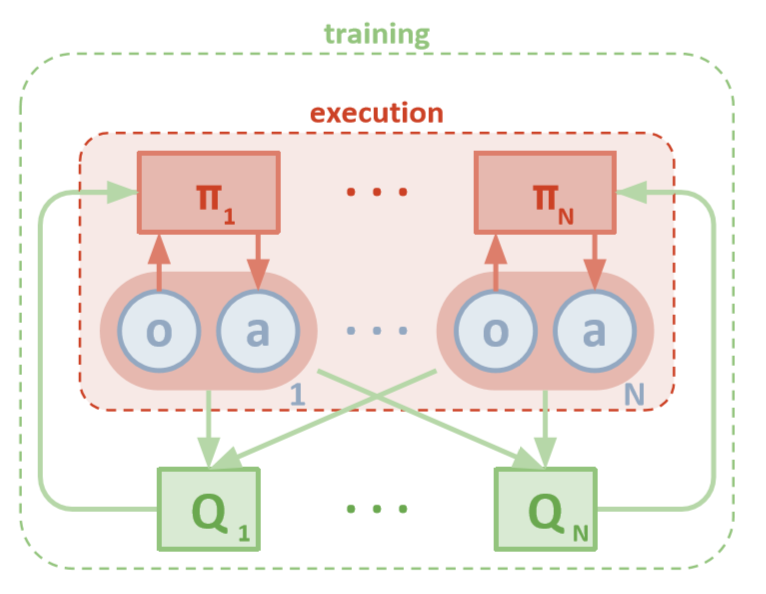
Arquitetura MADDPG (Lowe, 2018)
Treinamento
Primeiro, o MADDPG usa a repetição da experiência para um aprendizado efetivo fora da política . A cada intervalo de tempo, o agente armazena a seguinte transição:
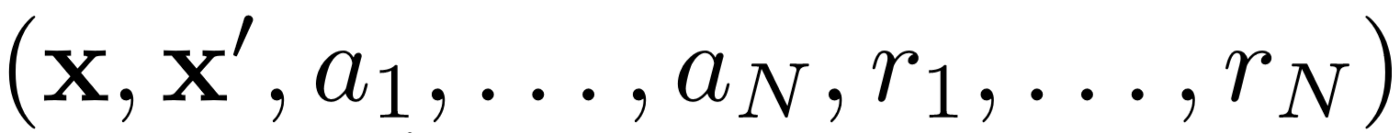
Onde armazenamos o estado conjunto, o próximo estado conjunto, a ação conjunta e cada uma das recompensas recebidas pelo agente. Em seguida, pegamos um conjunto dessas transições a partir da repetição da experiência para treinar nosso agente.
Atualizações críticas
Para atualizar o crítico central do agente, usamos o erro TD lookahead:
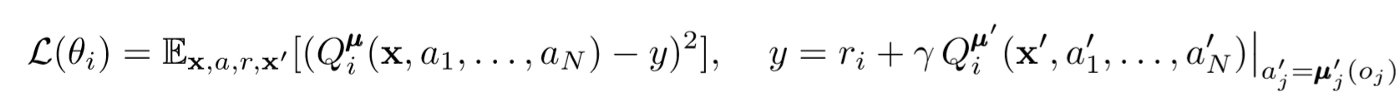
Onde μ é o ator. Lembre-se de que este é um crítico central, ou seja, ele usa informações gerais para atualizar seus parâmetros. A ideia básica é que, se você souber as ações que todos os agentes estão executando, o ambiente ficará parado, mesmo que a política seja alterada.
Preste atenção no lado direito da expressão com o cálculo do valor Q. Embora nunca salvemos nossa próxima sinergia, usamos cada ator-alvo do agente para calcular a próxima ação durante a atualização para tornar o aprendizado mais estável. Os parâmetros do ator de destino são atualizados periodicamente para corresponder aos parâmetros do ator do agente.
Atualizações dos atores
Semelhante ao DDPG de agente único, usamos um gradiente de política determinístico para atualizar cada parâmetro de um ator de agente.
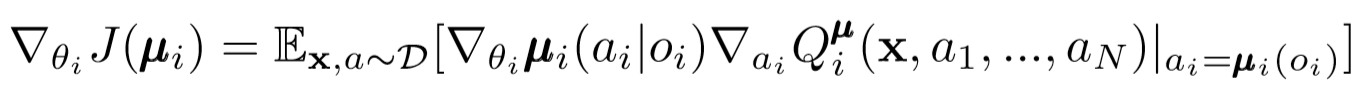
Onde μ é o ator do agente.
Vamos nos aprofundar um pouco mais nessa expressão de renovação. Tomamos o gradiente em relação aos parâmetros do ator usando o crítico central. O mais importante a ser observado é que, mesmo que o ator tenha apenas observações e ações locais, durante o treinamento, usamos um crítico central para obter informações sobre a otimização de suas ações em todo o sistema. Isso reduz o efeito da não estacionariedade, e a política de aprendizado permanece no espaço de estado inferior!
Conclusões de políticos e conjuntos de políticos
Podemos dar outro passo na questão da descentralização. Nas atualizações anteriores, assumimos que cada agente reconheceria automaticamente as ações de outros agentes. No entanto, o MADDPG propõe tirar conclusões das políticas de outros agentes, a fim de tornar o treinamento ainda mais independente. De fato, cada agente adicionará redes N-1 para avaliar a validade da diretiva de todos os outros agentes. Utilizamos uma rede probabilística para maximizar a probabilidade logarítmica de inferir a ação observada de outro agente.
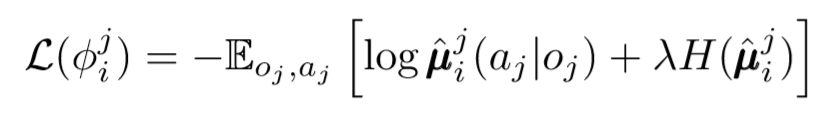
Onde vemos a função de perda para o i-ésimo agente avaliando a política do j-ésimo agente usando o regularizador de entropia. Como resultado, nosso valor Q desejado se torna um pouco diferente quando substituímos as ações do agente por nossas ações previsíveis!
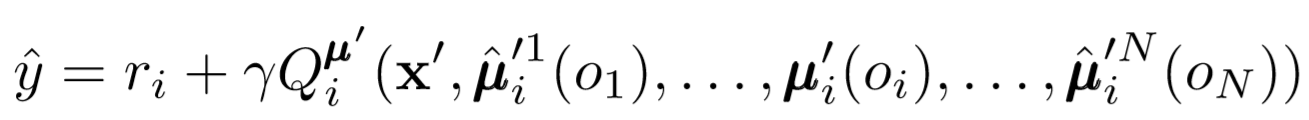
Então, o que aconteceu no final? Removemos a suposição de que os agentes conhecem as políticas um do outro. Em vez disso, tentamos treinar agentes para prever as políticas de outros agentes com base em uma série de observações. De fato, cada agente aprende de forma independente, recuperando informações globais do ambiente, em vez de simplesmente tê-las em mãos por padrão.
Conjuntos de políticos
Há um grande problema com a abordagem acima. Em muitas configurações de vários agentes, especialmente nas competitivas, os agentes podem criar políticas que podem treinar novamente o comportamento de outros agentes. Isso tornará a política frágil, instável e geralmente subótima. Para compensar essa falha, o MADDPG treina uma coleção de K subpolítica para cada agente. A cada etapa, o agente seleciona aleatoriamente uma das subpolíticas para selecionar a ação. E então executa.
O gradiente da política muda um pouco. Pegamos a média acima da subpolítica K, usamos linearidade de espera e propagamos atualizações usando a função de valor Q.
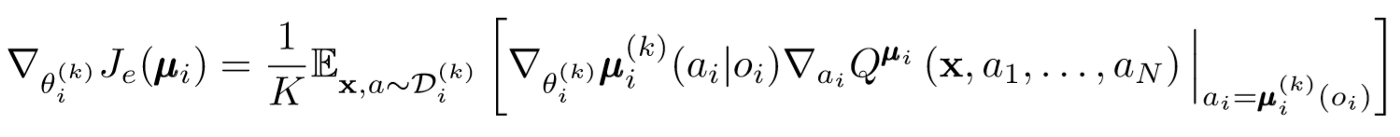
Dê um passo para trás
É assim que o algoritmo inteiro se parece em termos gerais. Agora precisamos voltar e perceber o que exatamente fizemos e entender intuitivamente por que funciona. Basicamente, fizemos o seguinte:
- Atores definidos para agentes que usam apenas observações locais. Dessa maneira, os efeitos negativos do aumento exponencial dos espaços de estado e ação podem ser controlados.
- Uma crítica central foi identificada para cada agente que usa informações compartilhadas. Portanto, fomos capazes de reduzir a influência da não estacionariedade e ajudamos o ator a se tornar ideal para o sistema global.
- Redes identificadas de conclusões das políticas para avaliar as políticas de outros agentes. Dessa maneira, conseguimos limitar a interdependência dos agentes e eliminar a necessidade de os agentes terem informações perfeitas.
- Os conjuntos de políticas foram identificados para reduzir o efeito e a possibilidade de reciclagem nas políticas de outros agentes.
Cada componente do algoritmo serve a um propósito específico e separado. O algoritmo MADDPG é poderoso por causa do seguinte: seus componentes são projetados especificamente para superar os sérios obstáculos que geralmente enfrentam sistemas multiagentes. A seguir, falaremos sobre o desempenho do algoritmo.
resultados
O MADDPG foi testado em muitos ambientes. Uma revisão completa de seu trabalho pode ser encontrada no artigo [1]. Aqui falaremos apenas sobre a tarefa da comunicação cooperativa.
Visão geral do ambiente
Existem dois agentes: o orador e o ouvinte. A cada iteração, o ouvinte recebe um ponto colorido no mapa para mover e recebe uma recompensa proporcional à distância desse ponto. Mas aqui está o problema: o ouvinte sabe apenas sua posição e a cor dos pontos finais. Ele não sabe para qual ponto ele deve ir. No entanto, o alto-falante sabe a cor do ponto desejado para a iteração atual. Como resultado, dois agentes devem interagir para resolver esse problema.
Comparação
Para resolver esse problema, o artigo contrasta o MADDPG e os métodos modernos de agente único. Melhorias significativas são vistas com o uso do MADDPG.
Também foi demonstrado que as conclusões dos políticos, mesmo que os políticos não tenham sido treinados perfeitamente, alcançaram os mesmos sucessos que podem ser alcançados usando observações verdadeiras. Além disso, não houve desaceleração significativa na convergência.
Finalmente, conjuntos de políticas mostraram resultados muito promissores. O artigo [1] explora o impacto de conjuntos em um ambiente competitivo e demonstra melhorias significativas de desempenho em relação a agentes de política única.
Conclusão
Isso é tudo. Aqui, analisamos uma nova abordagem para o aprendizado por reforço de múltiplos agentes. Obviamente, há um número infinito de métodos relacionados ao MARL, mas o MADDPG fornece uma base sólida para métodos que resolvem os problemas mais globais dos sistemas multiagentes.
Fontes
[1] R. Lowe, Y. Wu, A. Tamar, J. Harb, P. Abbeel, I. Mordatch, ator-crítico de múltiplos agentes para ambientes competitivos cooperativos mistos (2018).
Lista de artigos úteis
- 3 armadilhas para aspirantes a cientistas de dados
- Algoritmo AdaBoost
- Como foi o ano de 2019 no campo da matemática e da ciência da computação?
- O aprendizado de máquina enfrentou um problema de matemática não resolvido
- Compreendendo o Teorema de Bayes
- Procure contornos faciais em um milissegundo usando um conjunto de árvores de regressão
, , , . .