🤵🏼 🧐 🍑 Como confrontar matemáticos e especialistas em ML com a ajuda de um hackathon e quem vencerá 👨🏽‍🌾 📵 📩

Introdução

Este artigo é sobre como nós, junto com a subsidiária da Rosneft Samaraneftekhimproekt e a Universidade Federal de Kazan, realizamos o Hackathon de Três Cidades em setembro de 2020, onde convidamos alunos a resolver o problema clássico de correlação sísmica de horizontes refletivos. Esses são os desafios que os profissionais da sísmica em todo o mundo enfrentam diariamente. Para os participantes, eles decidiram apresentar o problema como "o problema de encontrar o caminho ideal" para não assustar os alunos com palavras terríveis. No artigo, falaremos mais sobre o problema e analisaremos as soluções interessantes dos participantes. Será empolgante tanto para modelagem matemática aplicada quanto para aprendizado de máquina e analistas de dados.

Parte organizacional

Descrevemos detalhes interessantes da organização de um hackathon online em três cidades em um artigo no vc.ru - Neftyanka e um hackathon. Uma maratona não significa apenas correr .

Mencionaremos apenas que para o formato online optamos pelo serviço Discord e deixaremos um link para as regras do hackathon (link no site Boosters ).

Formulação do problema

Na exploração sísmica, existe o conceito de “horizonte de reflexão sísmica” - é uma onda refletida, estável na dinâmica e área de propagação, que corresponde a um determinado limite geológico. Processando corretamente os dados sísmicos de campo e reconhecendo (dizem os especialistas em prospecção sísmica - "interpretando") os horizontes sísmicos, é possível determinar a profundidade de sua ocorrência com uma precisão de 5-10 metros. Determinadas as profundidades, então, em conjunto com os geólogos, é possível amarrar esses horizontes à escala geocronológica ( escala geocronológica - Wikipedia ) e reconhecer suas contrapartes menores. E então decida - entre quais horizontes podem estar as armadilhas de petróleo, como é o relevo do modelo estrutural do campo, etc.

imagem

Seções verticais do cubo sísmico e horizontes de reflexão sísmica reconhecidos

Na prática, os horizontes são diferenciados camada por camada nas seções sísmicas do cubo sísmico - ambos manualmente, usando uma matriz (dizem os especialistas sísmicos - "mergulho") de um grande número de pontos de referência e usando procedimentos de pesquisa automatizados e semiautomáticos ... Obviamente, uma solução de alta qualidade para o problema de interpretação de horizontes sísmicos usando software está em grande demanda e pode reduzir significativamente o tempo gasto por especialistas em prospecção sísmica.

Ao mesmo tempo, o estudo de fontes ( horizontes de mínimos quadrados com inclinações locais e correlações de múltiplas grades, Waveform Embedding: escolha automática de horizonte com aprendizado profundo não supervisionado) mostra que os algoritmos e soluções desenvolvidos são baseados em um pequeno número de abordagens matemáticas, então decidimos tentar atrair os alunos com sua consciência ainda não obscurecida pela pesquisa científica e oferecer-lhes este problema na forma de um problema de encontrar o caminho ideal em uma superfície complexa.

Como resultado, o problema foi formulado da seguinte forma: construção de um caminho de movimento em uma superfície complexa, passando por determinados pontos e satisfazendo as condições de um mínimo de algum funcional, dependendo do comprimento do caminho e seus ângulos (gradientes).

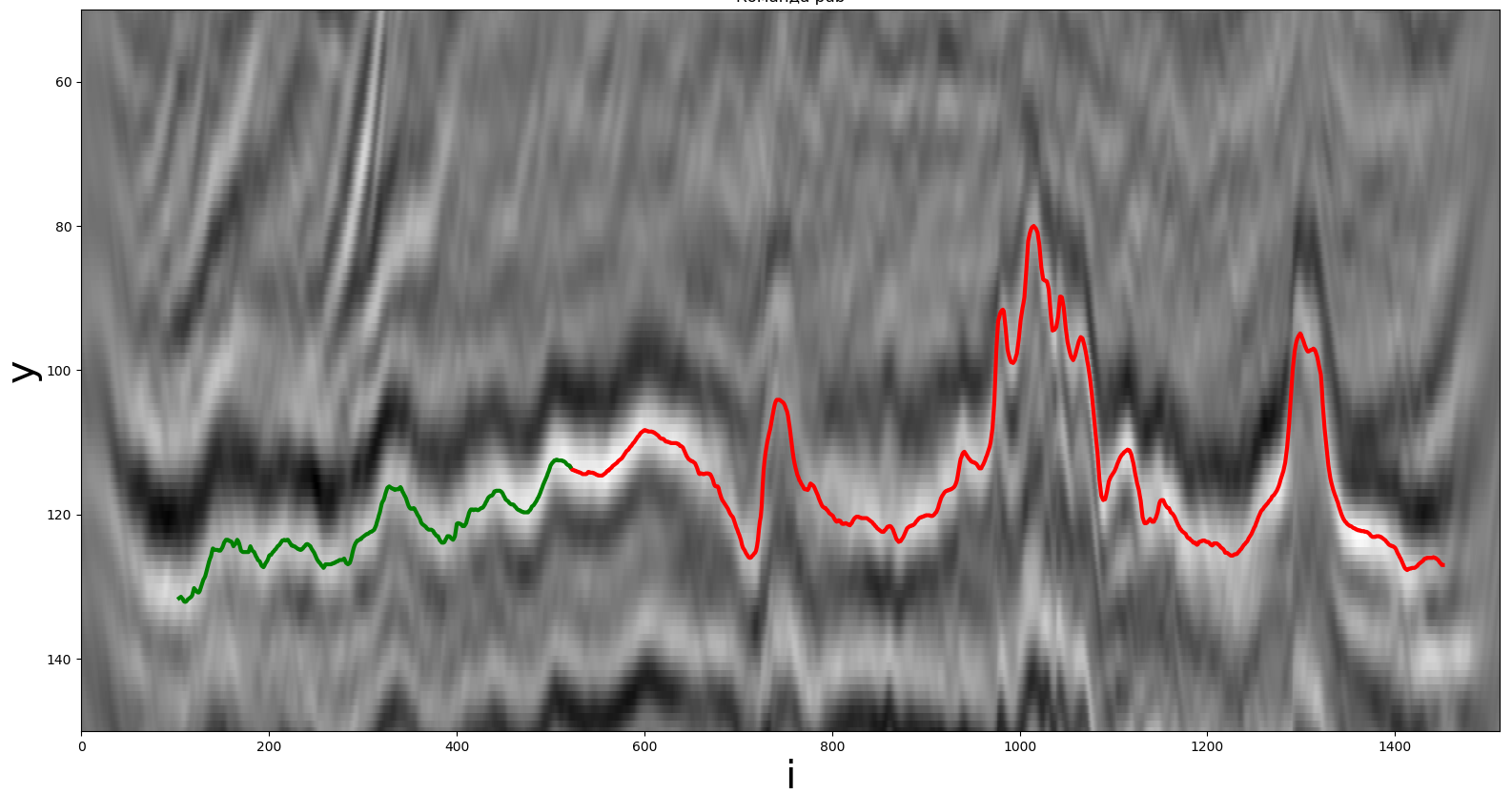
imagem

Um exemplo de uma parte da seção sísmica original para a construção de um horizonte. A linha verde é a parte conhecida de antemão, a linha vermelha é a parte desejada.

Os participantes da competição tinham que encontrar uma solução em 12 horas que lhes permitisse continuar seu caminho ao longo da trajetória ótima na parte oculta do conjunto de dados. Foram realizadas 20 tentativas de validação da solução e venceu o participante com o valor mínimo da métrica.

Descrição detalhada dos dados

, :

. , [x,y] z(x,y) .
(x,y) L1 L2. x, hor_1, …, hor_4.
L2 4 (1, 2, 3, 4), L1 – 3 (1, 3, 4). 2- L1 (40%). 60% .

, – 2 .

-, hor_2 L1. L2 L1. . , , .

Ao longo da competição, a classificação foi construída com base nos valores da métrica na parte pública dos dados de teste. Após o término da competição, o valor da métrica foi recalculado na parte privada, e a classificação foi atualizada. Isso é importante para se obter soluções sustentáveis, ou seja, não só sob medida para dados públicos, mas também capazes de apresentar um resultado comparável em dados privados. Descobriu-se que isso não foi feito em vão e, após a avaliação final de qualidade, a classificação mudou.

Para quantificar os resultados obtidos, foi utilizada a seguinte métrica:

F (\hat{y}, \hat{z}) = \sqrt{\sum_{i = 0}^{N} ({\hat{y}}_{i}^{p r e d} - {\hat{y}}_{i}^{e t a l o n}) + {(\hat{z} (i, y_{i}^{p r e d}) - \hat{z} (i, y_{i}^{e t a l o n}))}^{2}}

$F\left (\widehat{y},\widehat{z} \right ) = \sqrt{\sum_{i=0}^N\left(\widehat{y}_{i}^{pred} -\widehat{y}_{i}^{etalon} \right)+\left(\widehat{z}\left(i,y_i^{pred}\right) - \widehat{z}\left(i,y_i^{etalon} \right) \right)^2}$

onde:

N é a dimensão do horizonte necessário;

y_{i}^{p r e d}

${y}_{i}^{pred}$ - coordenadas do horizonte obtidas usando o algoritmo,

i \in \bar{0, N}

$i\in\overline{0,N}$ ;

y_{i}^{e t a l o n}

${y}_{i}^{etalon}$ - coordenadas do horizonte de referência;

\hat{z} (i, y_{i})

$\widehat{z}\left(i,y_i\right)$ - valores do mapa de superfície no ponto com as coordenadas i, yi;

{\hat{y}}_{i} = \frac{y_{i}}{h e i g h t}

$\widehat{y}_i = \frac{y_i}{{height}}$ , onde a altura é o valor máximo possível da coordenada y do mapa de superfície;

\hat{z} (i, y_{i}) = \frac{z (i, y_{i})}{m a x (z)}

$\widehat{z}\left(i,y_i\right) = \frac{z\left(i,y_i \right)}{{max \left(z \right)}}$ onde max (z) é o maior valor do mapa de superfície.

Implementação de métrica em Python

def score(true, submission, all_data):
   #true – pandas.Dataframe    ;
   #submission - pandas.Dataframe   , 
   #;
   #all_data - numpy.ndarray    
   all_data = all_data.astype('float64')
   #    
   max_z = abs(all_data).max()
   #   
   y_pred = submission.loc[idx.index.values].y.values.astype('int')
   #  
   y_true = true.y.astype(int)
   #     
   z_pred = all_data[true.index.values.astype(int), y_pred.astype(int)]
   #     
   z_true = all_data[true.index.values, y_true]
   #   
   y_err = ((y_pred - y_true)/3000)** 2
   z_err = ((z_pred - z_true)/max_z) ** 2
   #     
   total_err = np.sqrt(np.sum(y_err + z_err))
   return total_err

Quais métodos foram usados pelas equipes

O problema foi inicialmente selecionado de forma que pudesse ser resolvido de várias maneiras: direta e inversa (usando métodos matemáticos clássicos e métodos de aprendizado de máquina, respectivamente).

Do ponto de vista do aprendizado de máquina, o problema pode ser resolvido por dois métodos:

1) Construção da regressão

usando pares de pontos conhecidos (

x_{i}, y_{i}

$x_i,y_i$ ), você pode construir um mapeamento

f : ϕ (x_{i}) \mapsto y_{i}

$f:\phi \left(x_i \right)\mapsto y_i$ minimizando a função de perda L.

ϕ (x_{i})

$\phi \left(x_i \right)$ - descrição indicativa do i-ésimo ponto.

Por exemplo,

ϕ : x_{i} \mapsto x_{i}

$\phi : x_i \mapsto x_i$ ou

ϕ : x_{i} \mapsto (x_{i}, x_{i}^{2}, x_{i} \cdot x)

$\phi : x_i \mapsto \left( x_i,x_i^2,x_i \cdot x \right)$

A função de perda pode ser a função de erro inicial da declaração do problema ou uma função mais simples, por exemplo, o desvio padrão dos caminhos construídos e originais:

\frac{1}{N} \sum_{i = 0}^{N} {(y_{i} - {\hat{y}}_{i})}^{2}

$\frac{1}{N} \sum_{i=0}^N \left( y_i - \widehat{y}_i \right)^2$

Muitos métodos populares de aprendizado de máquina podem ser usados para construir o mapeamento f : começando com regressão polinomial, percorrendo uma floresta aleatória e redes neurais profundas.

Várias equipes adotaram essa abordagem usando como

ϕ

$\phi$ rede neural convolucional ou totalmente conectada e como f - rede neural ou processos gaussianos.

2) Segmentação semântica

imagem

Um exemplo de segmentação semântica

O problema original pode ser resolvido como um problema de visão computacional. Os pontos (x, y) são considerados pixels da imagem, onde a imagem inteira é o conjunto de dados inteiro, e o "brilho" do pixel (x, y) é o valor z (x, y). Para construir um caminho, você precisa atribuir uma das classes a cada pixel - 0 ou 1. A parte da imagem que está abaixo do caminho ou a inclui pertence à classe 0 e o resto - à classe 1. Uma solução doméstica para esse problema é uma rede neural totalmente convolucional U-Net, em uma entrada que recebe um pedaço (patch) da imagem original e produz um array do mesmo tamanho, consistindo de zeros e uns, denotando as classes dos pixels correspondentes.

Além das técnicas de aprendizado profundo, você também pode usar técnicas clássicas de visão computacional e processamento de imagem, como o preenchimento de flood para segmentação de imagem. Isso foi feito por um dos participantes, pré-processando assim a imagem para posterior aplicação de algoritmos para encontrar o caminho mais curto.

Do ponto de vista dos métodos matemáticos clássicos , o problema proposto é um problema de otimização clássico, e observamos tentativas de resolvê-lo pelos seguintes grupos de métodos:

, ;

. y , y, .
, ;

$y_i$ .
, .

, .

Primeiro, vamos analisar as decisões dos participantes.

Métodos de aprendizado de máquina:

uma das soluções foi uma rede neural convolucional autorregressiva que produz um número real - o valor do caminho

{\hat{y}}_{i}

$\widehat{y}_i$ para a i-ésima etapa. Os patches de 32x32 pixels da imagem original foram alimentados para a entrada da rede neural. Como uma função

ϕ

$\phi$ Para extração de recursos, uma rede neural convolucional pré-treinada ResNet34 foi usada. A representação de recursos obtida por essa rede neural foi combinada com os valores desse caminho das 32 etapas anteriores. Para prever mais 32 etapas, as previsões da rede neural anteriores foram usadas como os valores do horizonte anterior. A rede neural foi treinada por uma modificação da descida gradiente estocástica de Adam com uma diminuição exponencial na etapa do otimizador à medida que ela é treinada. Para o treinamento, o desvio absoluto médio foi minimizado (experimentos com o desvio padrão deram piores resultados). Para evitar overfitting, foi utilizado o Dropout, ou seja, zeramento aleatório de uma parte dos neurônios. Demorou cerca de 10 minutos para treinar a rede neural, 20 passagens completas em todo o conjunto de dados e 720 etapas do otimizador.

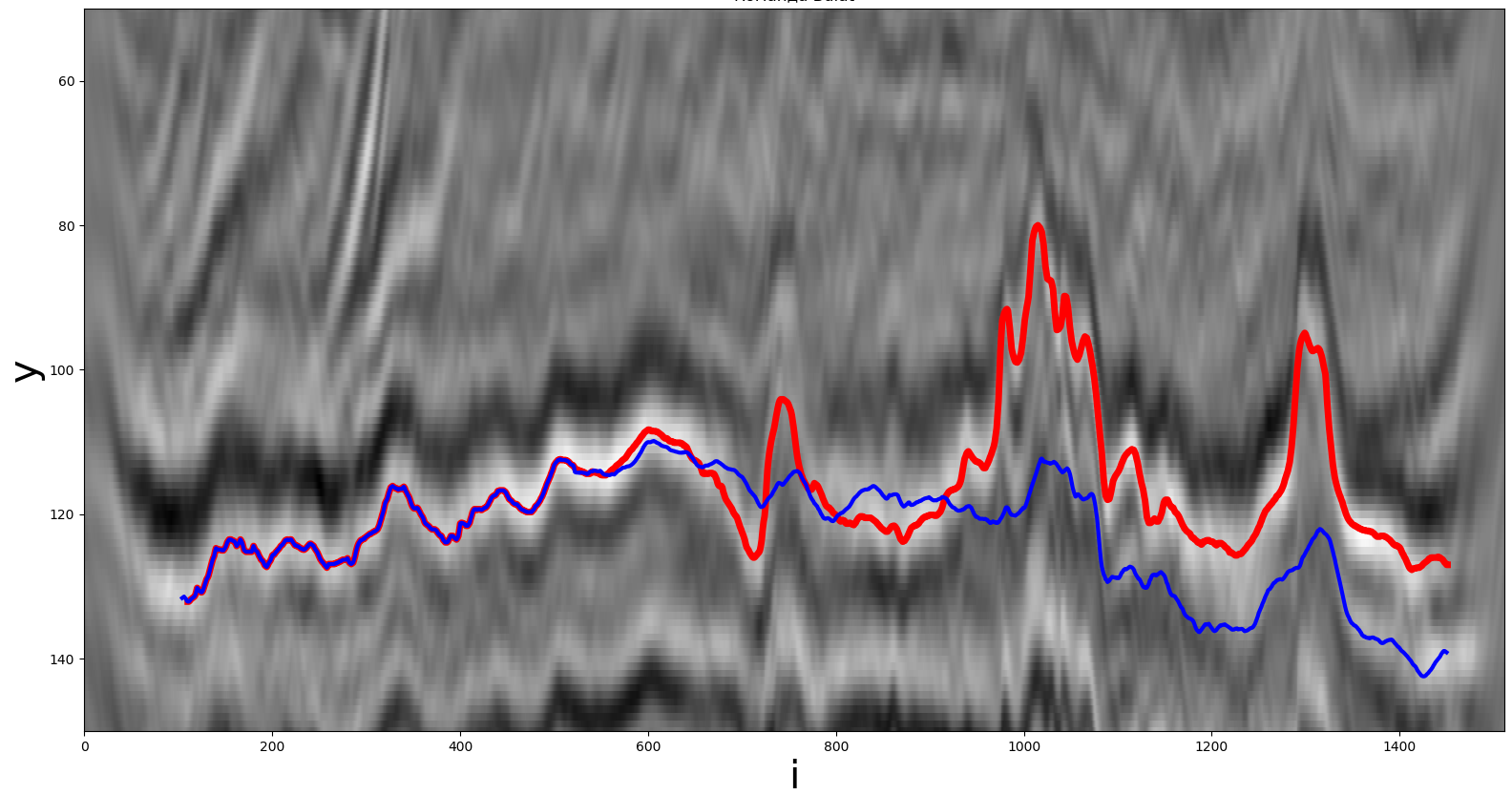
imagem

Uma solução obtida usando uma rede neural convolucional. A linha vermelha é o caminho real, a linha azul é aquela recebida pelo participante.

A previsão da rede neural leva cerca de 1 minuto em uma CPU AMD Threadripper 2950x e GPU Nvidia GTX 1080 Ti.

O resultado da rede neural (métrica) é 5,71 na classificação pública. Também foram feitos experimentos com a substituição da rede neural convolucional por uma recorrente, mas seu resultado foi pior. Como resultado, métodos clássicos de matemática computacional foram usados como a solução final.

Além das soluções acabadas, os participantes também compartilharam suas ideias, que não conseguiram implementar devido ao prazo apertado da competição e à complexidade computacional de suas ideias. Alguns deles tentaram aplicar redes neurais, mas depois de passar a maior parte do tempo, eles passaram para algoritmos mais simples e eficientes ou mesmo para força bruta e regras, que acabaram dando o melhor resultado e gerando prêmios.

Além disso, uma série de soluções interessantes são baseadas no conhecimento de outras disciplinas: por exemplo, visão computacional clássica e processamento de imagens, teoria dos grafos, análise de séries temporais. Uma das equipes até mesmo colocou o problema em termos de aprendizagem por reforço, de que você já deve ter ouvido falar, e veio com uma solução, mas infelizmente não conseguiu implementá-la.

Métodos matemáticos clássicos:

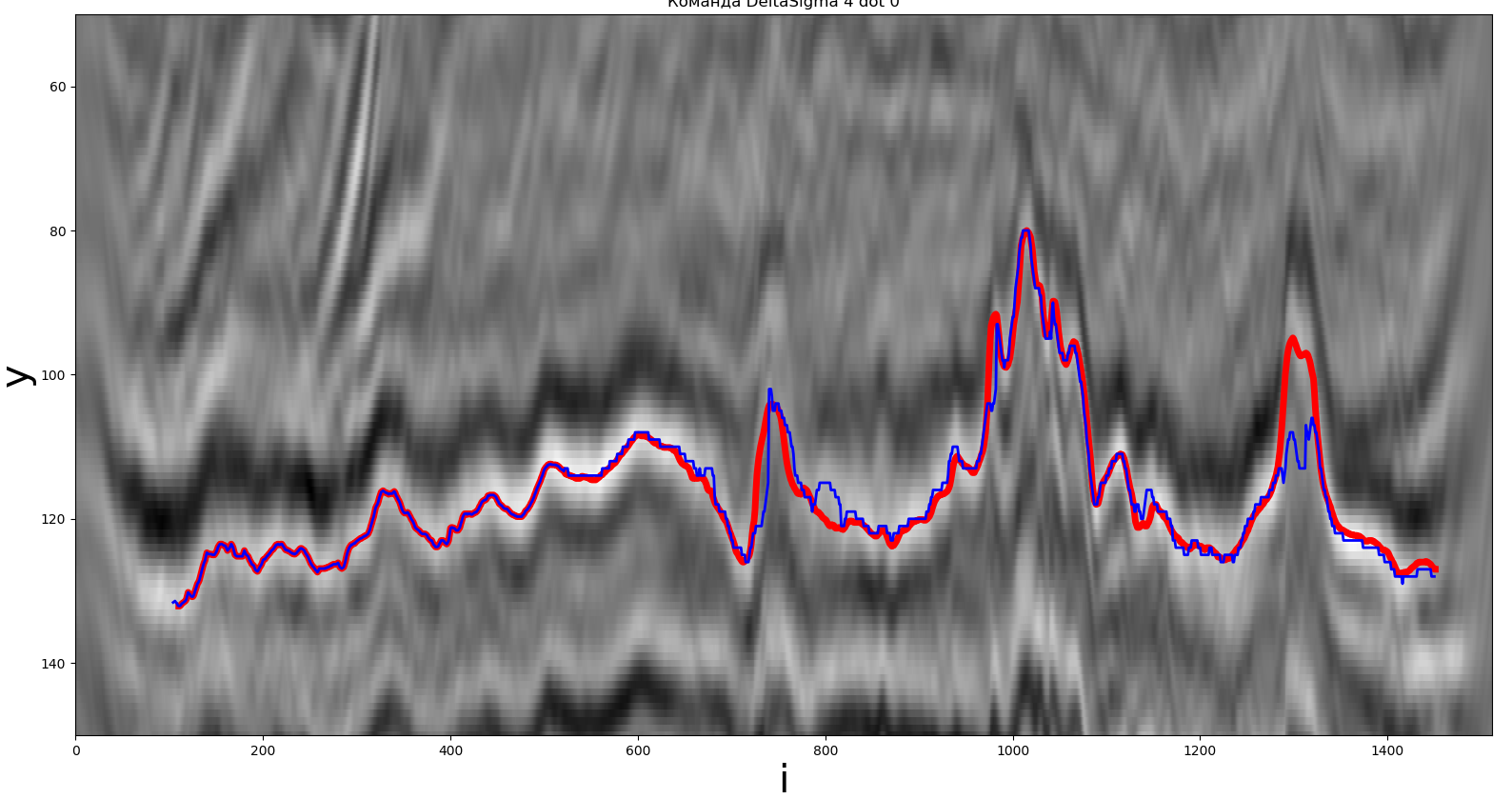
imagem

Uma das soluções obtidas pelo método extremo local. A linha vermelha é o caminho real, a linha azul é aquela recebida pelo participante.

Para este método, um máximo local foi usado como um extremo. O caminho construído pelos participantes está marcado em azul, o horizonte desejado está em vermelho. Uma descrição detalhada é fornecida abaixo.

y_{i + 1} = m i n | j - y_{i} |, \forall i \in \bar{0, N - 1}, j \in Ω,

$y_{i+1} = min \left| j-y_i \right|, \forall i \in \overline{0,N-1}, j \in \Omega,$

Ω = {m | z (i, m) > z (i, m - 1) \cap z (i, m) > z (i, m + 1), \forall m \in \bar{m_{1}, m_{2}}}

$\Omega = \left \{ m|z(i,m)> z(i,m-1) \cap z(i,m) > z(i,m+1), \forall m \in \overline {m_1,m_2} \right \}$ ,

m_{1} = m a x (1, y_{i} - s i z e_{y})

$m_1 = max(1,y_i - size_y)$ ,

m_{2} = m i n (h e i g h t - 1, y_{i} + s i z e_{y}

$m_2=min(height - 1,y_i + size_y$ ,

Onde:

h e i g h t

$height$ - o valor máximo possível da coordenada y do mapa de superfície;

s i z e_{y}

$size_y$ - o tamanho da janela de pesquisa.

O método é implementado em Python. O tempo de operação foi de cerca de 0,103 segundos, F (y, z) = 1,57,

s i z e_{y}

$size_y$ = 100.

Conclusão: o método é bastante simples de implementar, o tempo de execução não ultrapassa 0,1 segundos.

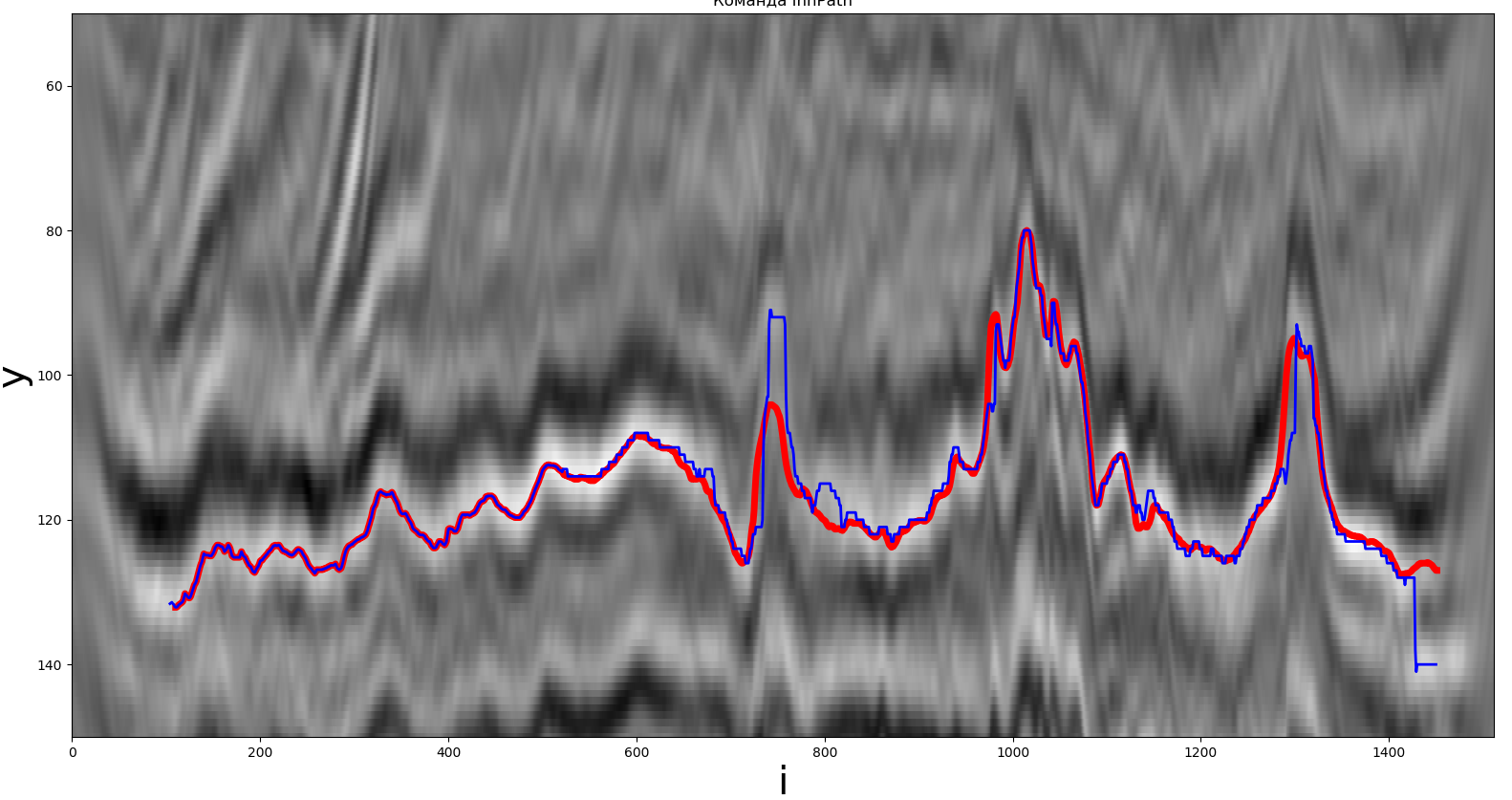
imagem

Uma das soluções obtidas pelo extremo global. A linha vermelha é o caminho real, a linha azul é aquela recebida pelo participante.

Vamos passar para o próximo grupo. Como antes, neste método, o máximo foi usado como um extremo.

y_{i} = a r g m a x (\frac{1}{s i z e_{x}} \sum_{j = 0}^{s i z e_{x} - 1} z (i + j, m))), \forall i \in \bar{0, N}, m \in \bar{m_{1}, m_{2}}

$y_i= {argmax}\left(\frac{1}{size_x} \sum_{{j=0}}^{{size_x-1}}z (i+j,m))\right), \forall i \in \overline {0,N}, m \in \overline{m_1,m_2}$ ,

m_{1} = m a x (1, y_{i} - s i z e_{y})

$m_1 = max(1,y_i - size_y)$ ,

m_{2} = m i n (h e i g h t - 1, y_{i} + s i z e_{y})

$m_2=min(height - 1,y_i + size_y)$ ,

onde:

height é o valor máximo possível da coordenada y do mapa de superfície;

s i z e_{x}, s i z e_{y}

$size_x,size_y$ - o tamanho da janela de pesquisa.

O método é implementado em Python. O tempo de operação foi de cerca de 0,19 segundos, F (y, z) = 1,97,

s i z e_{x}

$size_x$ = 9,

s i z e_{y}

$size_y$ = 21.

Conclusão: o método é bastante simples de implementar, o tempo de execução não ultrapassa 0,2 segundos.

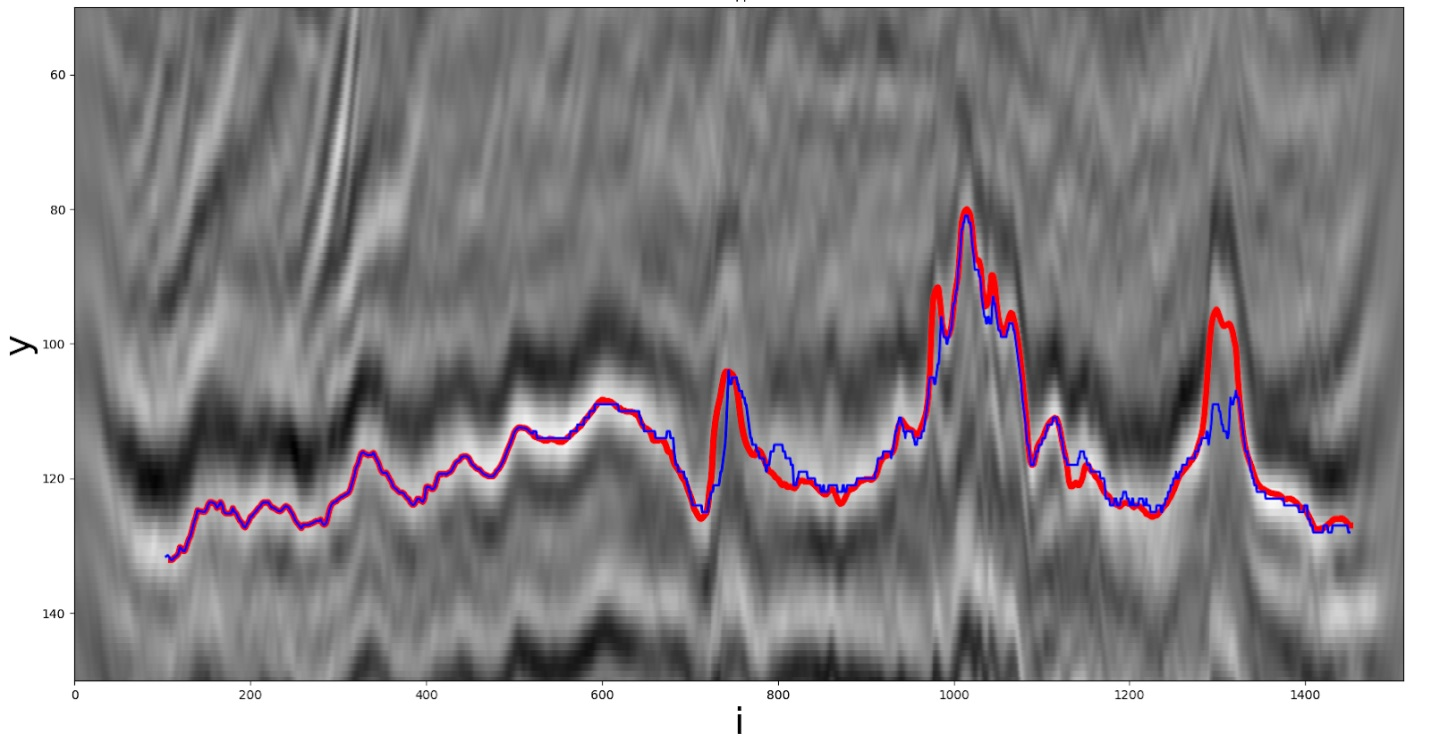
imagem

Uma das soluções heurísticas. A linha vermelha é o caminho real, a linha azul é aquela recebida pelo participante.

Vamos considerar o último grupo de métodos. Como mencionado anteriormente, a próxima coordenada

y_{i} + 1

$y_i+1$ é pesquisado pelo mínimo de funcionalidade na janela de pesquisa especificada.

A seguir, uma das funcionalidades propostas pelas equipes. Do ponto de vista matemático, é assim:

y_{i + 1} = m i n (\frac{(z (i, j) - z (i, y_{i}))^{2}}{m a x^{2} (z)} + α \frac{(j - y_{i})^{2}}{{h e i g h t}^{2}}), \forall i \in \bar{0, N - 1}, j \in Ω,

$y_{i+1}= {min}\left(\frac{(z(i,j)-z(i,y_i))^2}{max^2(z)} + \alpha \frac{(j-y_i)^2}{{height}^2}\right), \forall i \in \overline {0,N-1}, j \in \Omega,$

Ω = {m | z (i, m) > z (i, m - 1) \cap z (i, m) > z (i, m + 1), \forall m \in \bar{m_{1}, m_{2}}}

$\Omega = \left \{ m|z(i,m)>z(i,m-1)\cap z(i,m)>z(i,m+1), \forall m \in \overline {m_1,m_2} \right \}$

m_{1} = m a x (1, y_{i} - s i z e_{y})

$m_1 = max(1,y_i - size_y)$ ,

m_{2} = m i n (h e i g h t - 1, y_{i} + s i z e_{y})

$m_2=min(height - 1,y_i + size_y)$ ,

Onde:

h e i g h t

$height$ - o valor máximo possível da coordenada y do mapa de superfície;

α

$\alpha$ - coeficiente responsável pela influência do erro em y sobre o valor do funcional;

s i z e_{y}

$size_y$ - o tamanho da janela de pesquisa;

m a x (z)

$max(z)$ É o valor mais alto do mapa de superfície.

O método foi implementado em Python. O tempo de operação foi de cerca de 0,12 segundos, F (y, z) = 1,58,

s i z e_{y}

$size_y$ = 50,

α

$\alpha$ = 15000,7.

Conclusão: o tempo de execução do método não ultrapassa 0,15 segundos.

Os métodos de todos os três grupos mostraram resultados bastante semelhantes em um determinado conjunto de dados. O menor valor métrico (1,57) foi alcançado por um método baseado na busca por extremos locais de valores de superfície dentro de uma determinada janela de busca.

Parte final

Infelizmente, ao final do hackathon, quase todos os inovadores ~~passaram para o lado negro, se~~ reciclaram e se tornaram conservadores, ou seja, passaram a enviar soluções usando algoritmos clássicos ... e os conservadores venceram.

Queríamos reunir colaboradores de duas áreas: matemática computacional e aprendizado de máquina. Alguns estão acostumados a trabalhar com dados não estruturados de natureza desconhecida, enquanto outros estão acostumados a estudar processos físicos e construir modelos matemáticos com base nisso. Para aumentar a variedade de ideias e soluções, descrevemos brevemente como os dados foram obtidos. Esta é uma das razões pelas quais a solução baseada em métodos numéricos simples deu os melhores resultados. A segunda razão foi que, para o hackathon dos alunos, preparamos dados não muito "complexos" de um volume pequeno, de modo que os métodos laboriosos de aprendizado de máquina modernos perdem para alternativas mais simples.

Acreditamos que esta é uma excelente aula que ajudará os participantes a definir corretamente os problemas e escolher os melhores métodos para resolvê-los. É importante lembrar que primeiro você deve tentar uma solução simples, a chamada linha de base, talvez ela permita atingir seu objetivo em pouco tempo.

Os participantes do Hackathon propuseram seus próprios algoritmos para encontrar o caminho ideal em um conjunto de big data em relação ao problema de interpretação cinemática sísmica automática, que atualmente está sendo resolvido como parte do desenvolvimento de software corporativo na área de geologia e sísmica. As implementações mais competitivas de algoritmos encontrarão sua aplicação no desenvolvimento e implementação de módulos de software para esses sistemas de software.

Teremos o maior prazer em vê-lo na final da maratona de competição de TI, que será realizada online no dia 28 de novembro. O programa inclui: premiação aos vencedores do concurso, apresentação da primeira versão do aplicativo móvel para avaliação expressa da qualidade do propante. Além disso, no âmbito do evento, serão organizados painéis de discussão sobre os temas "Gestão de dados e projetos de DS" e "Visão computacional". Representantes do Chefe de Ciência de Dados Alfa, CDO Megafon, Huawei, Chefe de CV X5 e outros compartilharão casos interessantes.Não perca toda a diversão ( Competição de TI Maratona 2020 - Rosneft ).

Como confrontar matemáticos e especialistas em ML com a ajuda de um hackathon e quem vencerá

Introdução

Parte organizacional

Formulação do problema

Quais métodos foram usados ​​pelas equipes

Parte final

More articles:

Quais métodos foram usados pelas equipes