Na primeira parte, vimos a álgebra externa e percebemos que vetores normais em 3D podem ser interpretados como bivetores. Para transformar bivetores, no caso geral, é necessária uma matriz diferente daquela que transforma vetores comuns. Usando a base canônica para bivetores, descobrimos que esta é a matriz adjunta , que é proporcional à transposta inversa. Esse raciocínio explica, pelo menos parcialmente, por que as normais são transformadas pela matriz inversa transposta.
Mas algumas questões foram varridas para debaixo do tapete.
Consideramos matrizes adjuntas, mas não mostramos como elas se relacionam com a prova algébrica de que para transformar a equação do planoé necessária uma matriz de transposição inversa. A proporcionalidade entre as matrizes era, em certo sentido, rebuscada.
Além disso, vimos que -vetores de álgebra externa fornecem objetos geométricos vetoriais com uma interpretação natural, na qual eles contêm unidades de comprimento, área e volume, que mudam de acordo com a escala. Mas não encontramos nada parecido com isso para densidades - unidades inversas de comprimento, área e volume.
Neste artigo, veremos outro conceito geométrico que será necessário para completar a pintura. A fusão deste novo conceito com a álgebra externa já estudada irá esclarecer e resolver as questões restantes.
Funciona como vetores
, . , , , .
: , ,
. — , … , ? ?
, . , (). , , : ( ). .
! . , : . , , .
: ( , ) — . . , , "". .
. , .
, .
, , . , .
( : , . !)
(3D) (2D), / , . :
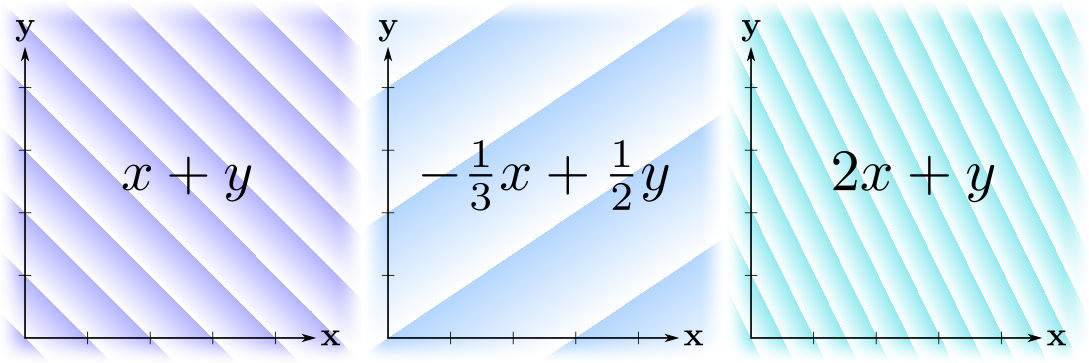
— . . , "́" ( ́ ) , .
, . , .
— — , : ( ) . . ( ) .
, — , , . - , , . , , .
, . . , — — , :
, — !
, : . .
, , , . , , "" . , — , … .
: . — , — . , . , — , .
:
, " " , .
. , , . :
. :
.
, , , . , . , . .
:
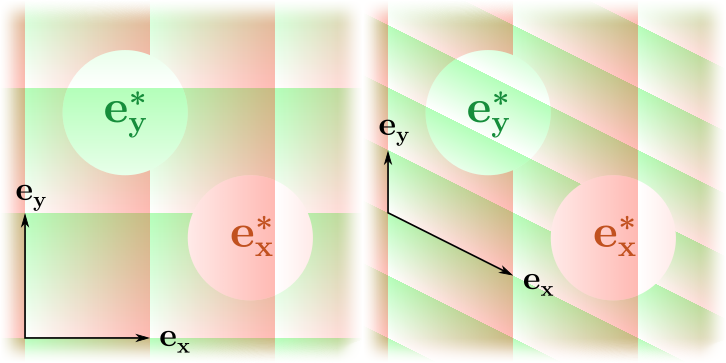
:
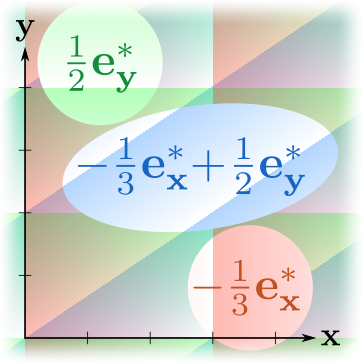
. :
, ( ), , , .
! "" ( ), ( 3D), ( ). !
— , . ?
: . , . : - . ( , ).
: , , . :
, , .
, . " " : .
, , . , . .
, . , ?
, , . , :
! , . "" "" . , , !
, . , (, , , //) - . ( ), " "" ?"
"". , , - , . .
. , , — , . .
. , :
:

? : .
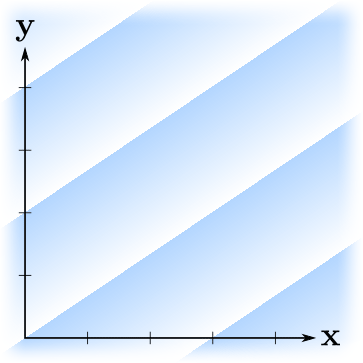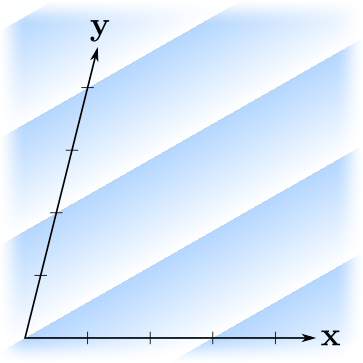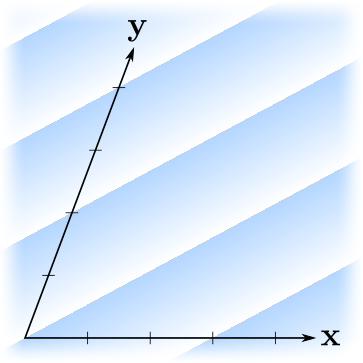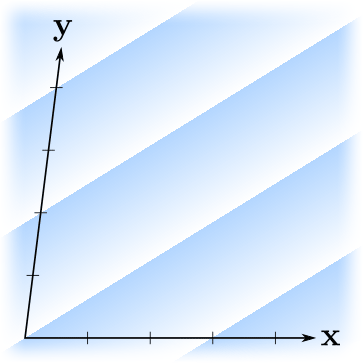
, ? . , — . ?
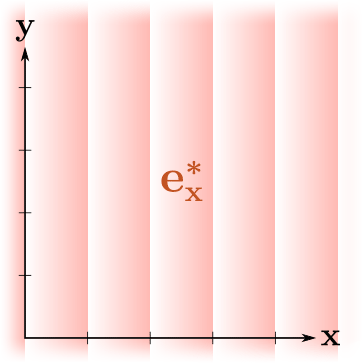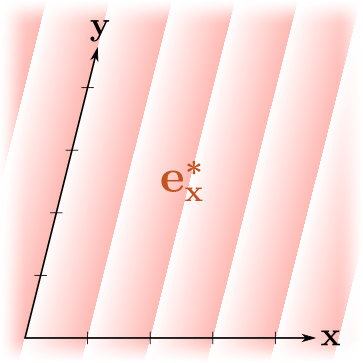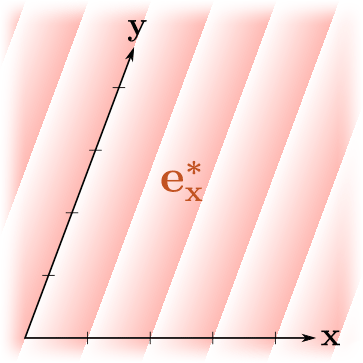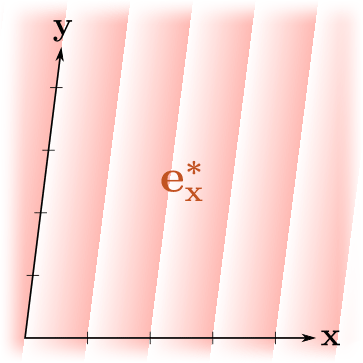
, ! , , , "" , . , .
, . , , , ,
!
, , . , , ( ), . :
.
, , .
?
, — 2D 3D. , , :
.
, , . :
, .
, , .
. , , , ? ?
, . " " , , . , : , . : , — .
Isso é tudo o que eu queria dizer sobre as transformações de vetores normais, mas mais algumas questões permaneceram no limbo. No final da primeira parte, fiz uma pergunta sobre graus negativos de escala. Agora temos menos o primeiro grau, mas e quanto a -2 e -3? Para entender isso, temos que combinar álgebra externa e espaços duais, o que faremos na terceira parte.