Os matemáticos há muito tentam se acostumar com o fato de que alguns problemas, em princípio, não podem ser resolvidos.

Gostamos de dizer que tudo é possível. No livro de Jaster Norton "Cute and the Magic Booth", o rei se recusa a informar Milo que seu objetivo é inatingível, porque "muito se torna possível se você não sabe que é impossível" [ embora essas sejam as palavras de outros personagens do livro / aprox. trad. ] Mas no mundo real, algumas coisas são realmente impossíveis e podemos prová-lo com a matemática.
As pessoas usam o termo "impossível" de muitas maneiras diferentes. Ele pode descrever apenas as coisas improváveis, como encontrar dois baralhos idênticos de cartas embaralhadas. Ele pode descrever tarefas que são quase impossíveis devido à falta de tempo, espaço ou recursos, como reescrever toda a Biblioteca do Congresso manualmente. Dispositivos como máquinas de movimento perpétuo são fisicamente impossíveis, uma vez que sua existência seria contrária ao nosso entendimento da física.
A impossibilidade matemática é diferente. Começamos com suposições inequívocas e, usando raciocínio matemático e lógica, concluímos que alguns resultados são impossíveis. Nenhuma quantidade de sorte, persistência, tempo ou habilidade tornará a tarefa factível. A história da matemática está repleta de provas de impossibilidade. Muitos deles são considerados os resultados mais notáveis da matemática. Mas não foi sempre assim.
A punição, talvez a primeira prova de impossibilidade, foi severa. Os historiadores acreditam que no século 5 aC. Hippasus of Metapont, um seguidor de Pitágoras, descobriu que era impossível encontrar um segmento de linha que pudesse medir tanto o comprimento lateral quanto o comprimento diagonal de um pentágono regular. Hoje dizemos que o comprimento da diagonal de um pentágono regular com comprimento lateral 1 é a proporção áurea, ϕ = 1/2 (1 + √5) - é um número irracional. A descoberta de Hipaso foi um desafio ao credo pitagórico, "tudo é número", portanto, as lendas dizem que Hipaso foi afogado no mar ou simplesmente expulso das fileiras dos pitagóricos.
Mais de um século depois, Euclides elevou a linha e o círculo como curvas fundamentais da geometria. Posteriormente, muitas gerações de geômetras desenharam todos os tipos de coisas - ângulos divisores, perpendiculares e assim por diante - apenas com a ajuda de um compasso e uma régua. No entanto, certas estruturas, que pareciam simples, intrigaram geômetras gregos, adquiriram um status mítico como resultado, e incomodaram os matemáticos por mais de 2.000 anos. Estes são os problemas de dividir um ângulo arbitrário em três partes, construir o lado de um cubo, o volume do qual é duas vezes o volume do dado, construir todos os polígonos regulares e também construir um quadrado com uma área igual à área de um determinado círculo.
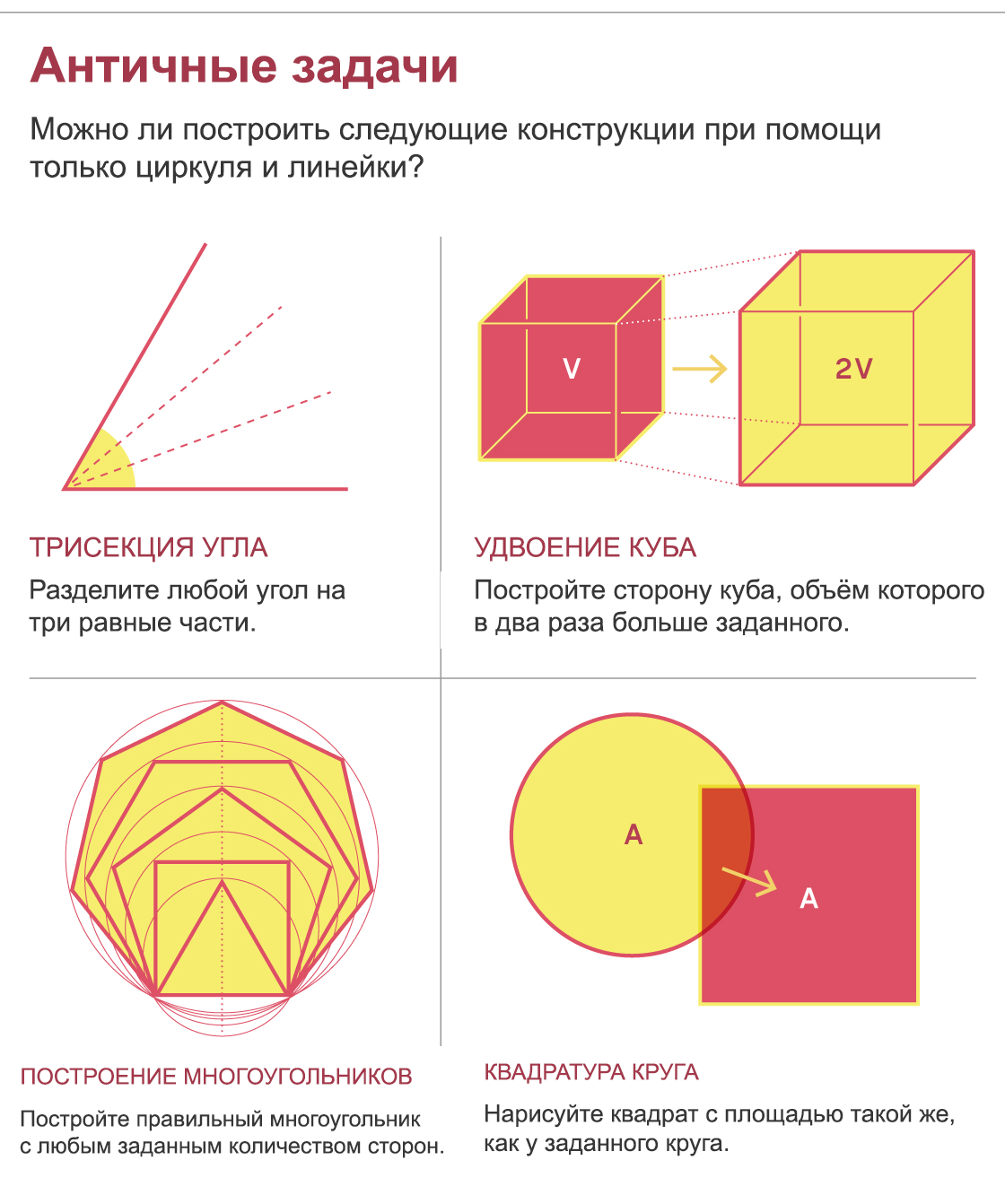
Embora esses problemas sejam de natureza geométrica, a prova de que não podem ser resolvidos não é. Uma nova matemática foi necessária para demonstrar a impossibilidade de resolvê-los.
No século XVII, René Descartes fez uma descoberta fundamental: se nos limitarmos a um compasso e uma régua, não poderemos desenhar segmentos de qualquer comprimento. Se começarmos com uma linha de comprimento 1, só podemos construir linhas cujo comprimento pode ser expresso usando inteiros, adição, subtração, multiplicação, divisão e raiz quadrada (como a proporção áurea).
Portanto, uma das estratégias para encontrar a prova da impossibilidade de resolver um problema geométrico - ou seja, de que determinado objeto não pode ser construído - será mostrar que o comprimento de um determinado segmento da figura final não pode ser expresso dessa forma. Mas, para mostrar isso com rigor, a álgebra então emergente foi necessária.
Dois séculos depois, o compatriota de Descartes, Pierre Laurent Vanzel , usou polinômios (somas de coeficientes e variáveis elevadas a uma potência) e suas raízes (variáveis que tornam o polinômio igual a zero) para atacar esses problemas clássicos. Por exemplo, no problema de dobrar um cubo, o lado de um cubo com um volume duas vezes maior que o de um cubo unitário deve ser igual a... Esta é a raiz do polinômio x 3 -2 porque...
Em 1837, Wanzel provou que para que um segmento seja construído usando um compasso e uma régua, seu comprimento deve ser a raiz de um polinômio que não pode ser fatorado e cuja potência (a maior potência da variável) é uma potência de dois. Por exemplo, a proporção áurea é a raiz do polinômio de segundo grau x 2 - x - 1. Mas x 3 -2 é um polinômio de terceiro grau, entãovocê não pode construir. Assim, Wanzel concluiu que dobrar o cubo era impossível.
De maneira semelhante, ele provou que é impossível usar ferramentas clássicas para trissecionar qualquer ângulo ou construir certos polígonos regulares - por exemplo, um de sete lados. Curiosamente, todas as três provas de impossibilidades foram publicadas na mesma página. Como Isaac Newton e Albert Einstein tiveram seus annus mirabilis (anos de milagres), essa situação pode ser chamada de pagina mirabilis - uma página de milagres.
Provar a impossibilidade do problema remanescente, quadrar o círculo, exigia algo novo. Em 1882 Ferdinand von Lindemannprovou o ponto-chave - que o número π não pode ser construído - provando sua transcendência, isto é, que não é uma raiz de nenhum polinômio.
Esses problemas clássicos podem ser atribuídos a uma má reputação e considerados sirenes que levaram os matemáticos a se espatifar nas rochas afiadas da impossibilidade. Mas eu os considero musas que inspiraram gerações de pensadores criativos.
O mesmo se aplica à tarefa impossível mais recente que surge de um ato tão simples como cruzar uma ponte. Imagine que você more em Pittsburgh, uma “cidade de pontes”, como muitos de meus alunos. Qualquer ciclista aventureiro pode se perguntar se, começando um passeio de casa, pode cruzar cada uma das 22 pontes que cruzam os principais rios de Pittsburgh exatamente uma vez e voltar para casa.
Em 1735, o prefeito prussiano definiu tarefa semelhante para Leonard Euler, apenas para Königsberg (hoje Kaliningrado). Sete pontes desta cidade ligam as três margens do rio e a ilha. A princípio, Euler descartou esse problema como não sendo matemático: "Soluções desse tipo têm pouco a ver com matemática, e não entendo por que você espera que um matemático dê isso a você, e não a outra pessoa."
Porém, logo Euler comprovou a impossibilidade de resolver esse problema e, no processo, criou uma nova área da matemática, que chamou de geometria dos arranjos - o que hoje chamamos de topologia. Ele percebeu que os detalhes específicos - a localização exata das pontes, a forma das parcelas de terreno, etc. - não eram importantes. Apenas suas conexões eram importantes. Mais tarde, os matemáticos refinaram as formulações de Euler usando o que hoje chamamos de gráficos. A ideia de conectividade está no centro do aprendizado sobre mídia social, internet, epidemiologia, lingüística, planejamento de rotas e muito mais.
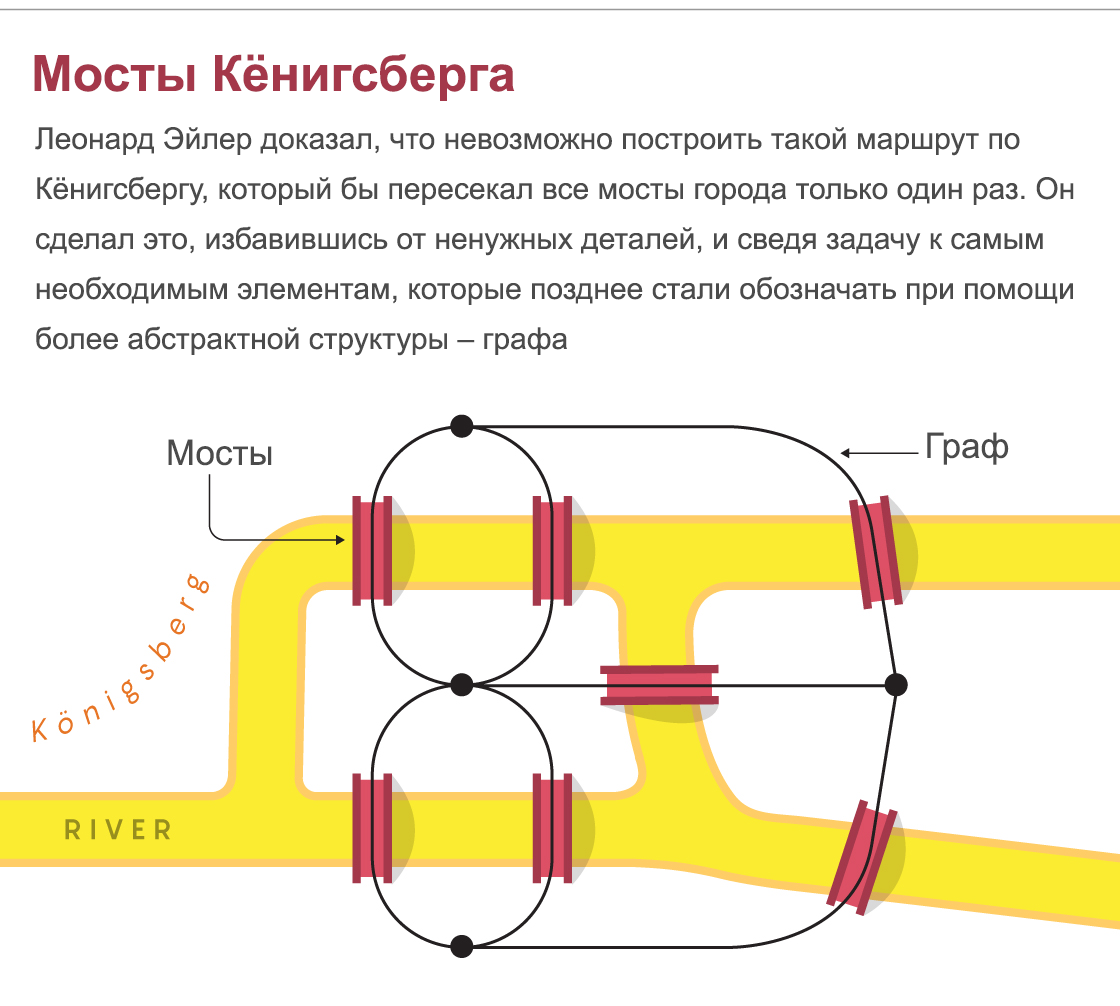
Pontes de Königsberg: Leonard Euler provou que é impossível construir uma rota ao longo de Königsberg que cruze todas as pontes da cidade apenas uma vez. Ele fez isso livrando-se de detalhes desnecessários e reduzindo o problema aos elementos mais necessários, que mais tarde passaram a ser designados com uma estrutura mais abstrata - o gráfico.
A prova de Euler era surpreendentemente simples. Ele raciocinou que toda vez que entramos e saímos de um determinado pedaço de terra, devemos eliminar duas pontes. Portanto, um número par de pontes deve ser conectado a cada pedaço de terreno. Mas, como um número ímpar de pontes conduzia a cada seção de Königsberg, era impossível construir essa rota. Da mesma forma, as três pontes que levam à ilha Gers no rio Allegheny em Pittsburgh tornam impossível construir a rota desejada para bicicletas.
Como mostra esse problema, as impossibilidades não se limitam à matemática abstrata. Eles podem ter consequências no mundo real - às vezes até políticas.
Recentemente, os matemáticos se voltaram para o conceito de gerrymendering . Nos Estados Unidos, após cada censo, os estados devem refazer os constituintes. Mas às vezes o partido governante reescreve suas fronteiras de maneiras ridículas para maximizar seu poder político.
Muitos estados exigem distritos “compactos” que não possuem uma definição matemática estrita. Em 1991, Daniel Paulsby e Robert Popper propuseram 4πA / P 2como forma de medir a compactação da área A e do perímetro P. Estes valores variam de 1 para uma freguesia redonda a quase zero para concelhos deformados com perímetro longo.
Enquanto isso, Nicholas Stephanopoulos e Eric McGee introduziram a “lacuna de desempenho” em 2014 como uma medida da integridade política de um plano de mudança distrital. Duas estratégias diferentes de gerrymandering são para que a oposição tenha menos de 50% dos votos ou cerca de 100%. Cada uma dessas táticas faz com que a oposição perca votos, perdendo os candidatos certos ou desperdiçando votos nos que não o fazem. A lacuna de eficiência descreve o número relativo de votos perdidos.
Ambas as medidas são úteis para reconhecer gerrymandering. Mas em 2018 Boris Alekseev e Dustin Mixonprovou que "às vezes pequenas lacunas de eficiência podem ser alcançadas com condados de formato estranho." Ou seja, é matematicamente impossível sempre desenhar condados para satisfazer os requisitos de Paulsby-Popper e a integridade da lacuna de eficiência.
No entanto, detectar e prevenir técnicas de gerrymandering sub-reptícias é um campo em rápido crescimento que atrai muitos esforços de pesquisa talentosos. Tal como acontece com os problemas da antiguidade ou com o problema das pontes de Königsberg, tenho certeza de que o problema gerrymandering inspirará a criatividade e contribuirá para o desenvolvimento da matemática.