
Auto identificação
Meu nome é Alexander, estou desenvolvendo a direção de análise de dados e tecnologia para fins de auditoria interna do grupo Rosbank. Minha equipe e eu usamos aprendizado de máquina e redes neurais para identificar riscos como parte das auditorias internas. Em nosso arsenal existe um servidor de ~ 300 GB de RAM e 4 processadores com 10 núcleos cada. Para programação ou modelagem algorítmica, usamos Python.
Introdução
Deparamo-nos com a tarefa de analisar fotografias (retratos) de clientes tiradas por bancários durante o registo de um produto bancário. Nosso objetivo é identificar riscos previamente descobertos nessas fotografias. Para identificar o risco, geramos e testamos um conjunto de hipóteses. Neste artigo, descreverei quais hipóteses criamos e como as testamos. Para simplificar a percepção do material, usarei a Mona Lisa - o padrão do gênero retrato.

Verificar soma
No início, adotamos uma abordagem sem aprendizado de máquina e sem visão computacional, apenas comparando as somas de verificação dos arquivos. Para gerá-los, pegamos o algoritmo md5 amplamente usado da biblioteca hashlib.
Implementação Python *:
#
with open(file,'rb') as f:
#
for chunk in iter(lambda: f.read(4096),b''):
#
hash_md5.update(chunk)
Ao formar a soma de verificação, verificamos imediatamente se há duplicatas usando um dicionário.
#
for file in folder_scan(for_scan):
#
ch_sum = checksum(file)
#
if ch_sum in list_of_uniq.keys():
# , , dataframe
df = df.append({'id':list_of_uniq[chs],'same_checksum_with':[file]}, ignore_index = True)
Este algoritmo é incrivelmente simples em termos de carga computacional: em nosso servidor 1000 imagens são processadas em no máximo 3 segundos.
Esse algoritmo nos ajudou a identificar fotos duplicadas entre nossos dados e, com isso, encontrar locais para possíveis melhorias no processo de negócios do banco.
Pontos-chave (visão computacional)
Apesar do resultado positivo do método de checksum, entendemos perfeitamente que se pelo menos um pixel da imagem for alterado, seu checksum será radicalmente diferente. Como um desenvolvimento lógico da primeira hipótese, assumimos que a imagem poderia ser alterada na estrutura de bits: sofrer resave (isto é, recompressão de jpg), redimensionar, cortar ou girar.
Para demonstração, vamos cortar as bordas ao longo do contorno vermelho e girar a Mona Lisa 90 graus para a direita.

Nesse caso, as duplicatas devem ser procuradas pelo conteúdo visual da imagem. Para isso, decidimos usar a biblioteca OpenCV, um método para construir pontos-chave de uma imagem e encontrar a distância entre os pontos-chave. Na prática, os pontos-chave podem ser cantos, gradientes de cor ou saliências de superfície. Para nossos propósitos, um dos métodos mais simples surgiu - Brute-Force Matching. Para medir a distância entre os pontos-chave da imagem, usamos a distância de Hamming. A imagem abaixo mostra o resultado da busca por pontos-chave nas imagens originais e modificadas (os 20 pontos-chave mais próximos das imagens são desenhados).
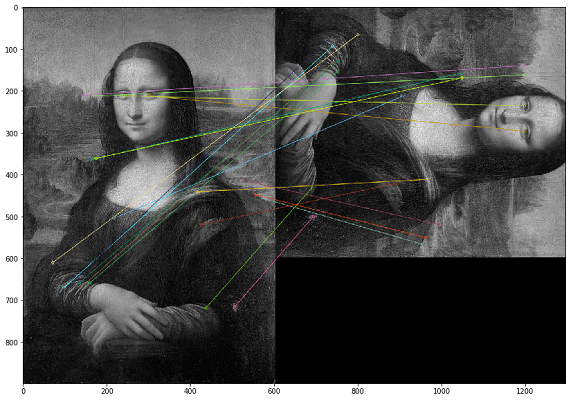
É importante notar que estamos analisando imagens em um filtro preto e branco, pois isso otimiza o tempo de execução do script e dá uma interpretação mais inequívoca dos pontos-chave. Se uma imagem tiver um filtro sépia e a outra um original colorido, quando as convertermos em um filtro preto e branco, os pontos-chave serão identificados independentemente do processamento de cores e dos filtros.
Amostra de código para comparar duas imagens *
img1 = cv.imread('mona.jpg',cv.IMREAD_GRAYSCALE) #
img2 = cv.imread('mona_ch.jpg',cv.IMREAD_GRAYSCALE) #
# ORB
orb = cv.ORB_create()
# ORB
kp1, des1 = orb.detectAndCompute(img1,None)
kp2, des2 = orb.detectAndCompute(img2,None)
# Brute-Force Matching
bf = cv.BFMatcher(cv.NORM_HAMMING, crossCheck=True)
# .
matches = bf.match(des1,des2)
# .
matches = sorted(matches, key = lambda x:x.distance)
# 20
img3 = cv.drawMatches(img1,kp1,img2,kp2,matches[:20],None,flags=cv.DrawMatchesFlags_NOT_DRAW_SINGLE_POINTS)
plt.imshow(img3),plt.show()
Ao testar os resultados, percebemos que, no caso da imagem invertida, a ordem dos pixels dentro do ponto-chave muda e essas imagens não são identificadas como iguais. Como medida compensatória, você mesmo pode espelhar cada imagem e analisar o dobro do volume (ou até o triplo), o que é muito mais caro em termos de capacidade de computação.
Esse algoritmo possui alta complexidade computacional, sendo que a maior carga é gerada pela operação de cálculo da distância entre pontos. Visto que temos que comparar cada imagem com cada uma, então, como você entende, o cálculo de tal conjunto cartesiano requer um grande número de ciclos computacionais. Em uma auditoria, um cálculo semelhante levou mais de um mês.
Outro problema com essa abordagem foi a má interpretabilidade dos resultados dos testes. Obtemos o coeficiente das distâncias entre os pontos-chave das imagens, e surge a pergunta: "Qual limite desse coeficiente deve ser escolhido o suficiente para considerar as imagens duplicadas?"
Usando a visão computacional, fomos capazes de encontrar casos que não foram cobertos pelo primeiro teste de checksum. Na prática, eles acabaram sendo arquivos jpg salvos em excesso. Não identificamos casos mais complexos de alterações de imagem no conjunto de dados analisado.
Pontos-chave de soma de verificação VS
Tendo desenvolvido duas abordagens radicalmente diferentes para localizar duplicatas e reutilizá-las em várias verificações, chegamos à conclusão de que, para nossos dados, a soma de verificação fornece um resultado mais tangível em um tempo mais curto. Portanto, se tivermos tempo suficiente para verificar, faremos uma comparação por pontos-chave.
Procure por imagens anormais
Depois de analisar os resultados do teste para pontos-chave, percebemos que as fotos tiradas por um funcionário têm aproximadamente o mesmo número de pontos-chave próximos. E isso é lógico, porque se ele se comunicar com os clientes em seu local de trabalho e tirar fotos na mesma sala, o fundo de todas as suas fotos será o mesmo. Esta constatação levou-nos a crer que podemos encontrar fotos excepcionais, diferentes das outras fotos deste colaborador, que podem ter sido tiradas fora do escritório.
Voltando ao exemplo com Mona Lisa, verifica-se que outras pessoas aparecerão contra o mesmo fundo. Mas, infelizmente, não encontramos esses exemplos, portanto, nesta seção mostraremos métricas de dados sem exemplos. Para aumentar a velocidade do cálculo no âmbito do teste dessa hipótese, decidimos abandonar os pontos-chave e usar histogramas.
O primeiro passo é traduzir a imagem em um objeto (histograma) que podemos medir para comparar as imagens pela distância entre seus histogramas. Basicamente, um histograma é um gráfico que fornece uma visão geral da imagem. Este é um gráfico com valores de pixel no eixo das abcissas (eixo X) e o número correspondente de pixels na imagem ao longo do eixo das ordenadas (eixo Y). Um histograma é uma maneira fácil de interpretar e analisar uma imagem. Usando o histograma de uma imagem, você pode ter uma ideia intuitiva de contraste, brilho, distribuição de intensidade e assim por diante.
Para cada imagem, criamos um histograma usando a função calcHist do OpenCV.
histo = cv2.calcHist([picture],[0],None,[256],[0,256])
Nos exemplos dados para três imagens, nós os descrevemos usando 256 fatores ao longo do eixo horizontal (todos os tipos de pixels). Mas também podemos reorganizar os pixels. Nossa equipe não fez muitos testes nesta parte, pois o resultado foi muito bom usando 256 fatores. Se necessário, podemos alterar este parâmetro diretamente na função calcHist.
Depois de criar os histogramas para cada imagem, podemos simplesmente treinar o modelo DBSCAN a partir das imagens de cada funcionário que fotografou o cliente. O ponto técnico aqui é selecionar os parâmetros DBSCAN (epsilon e min_samples) para nossa tarefa.
Depois de usar o DBSCAN, podemos fazer o clustering de imagens e, em seguida, aplicar o método PCA para visualizar os clusters resultantes.

Como pode ser visto pela distribuição das imagens analisadas, temos dois agrupamentos azuis pronunciados. Como se viu, em dias diferentes, um funcionário pode trabalhar em escritórios diferentes - as fotos tiradas em um dos escritórios criam um cluster separado.
Já os pontos verdes são fotos de exceção, onde o fundo é diferente desses aglomerados.
Após uma análise detalhada das fotos, encontramos muitas fotos falsamente negativas. Os casos mais comuns são fotografias estouradas ou em que grande parte da área é ocupada pelo rosto do cliente. Acontece que este método de análise requer intervenção humana obrigatória para validar os resultados.
Usando essa abordagem, você pode encontrar anomalias interessantes na foto, mas levará um investimento de tempo para analisar manualmente os resultados. Por esses motivos, raramente executamos esses testes como parte de nossas auditorias.
Existe um rosto na foto? (Detecção de rosto)
Portanto, já testamos nosso conjunto de dados de diferentes lados e, continuando a desenvolver a complexidade dos testes, passamos para a próxima hipótese: há um rosto do cliente em potencial na foto? Nossa tarefa é aprender como identificar rostos em imagens, fornecer funções para inserir uma imagem e obter o número de rostos na saída.
Este tipo de implementação já existe, e decidimos escolher MTCNN (Multitasking Cascade Convolutional Neural Network) para nossa tarefa a partir do módulo FaceNet do Google.
FaceNet é uma arquitetura de aprendizado de máquina profunda que consiste em camadas convolucionais. FaceNet retorna um vetor de 128 dimensões para cada face. Na verdade, FaceNet são várias redes neurais e um conjunto de algoritmos para preparar e processar os resultados intermediários dessas redes. Decidimos descrever a mecânica da busca facial por essa rede neural com mais detalhes, uma vez que não há tantos materiais sobre isso.
Etapa 1: pré-processamento
A primeira coisa que o MTCNN faz é criar vários tamanhos de nossa foto.
O MTCNN tentará reconhecer rostos dentro de um quadrado de tamanho fixo em cada fotografia. Usar esse reconhecimento na mesma foto de tamanhos diferentes aumentará nossas chances de reconhecer corretamente todos os rostos na foto.

Um rosto pode não ser reconhecido em um tamanho de imagem normal, mas pode ser reconhecido em uma imagem de tamanho diferente em um quadrado de tamanho fixo. Esta etapa é realizada algoritmicamente sem uma rede neural.
Etapa 2: P-Net
Depois de criar diferentes cópias de nossa foto, a primeira rede neural, P-Net, entra em ação. Esta rede usa um kernel 12x12 (bloco) que irá escanear todas as fotos (cópias da mesma foto, mas em tamanhos diferentes), começando do canto superior esquerdo, e se mover ao longo da imagem usando um passo de 2 pixels.

Depois de digitalizar todas as fotos de tamanhos diferentes, o MTCNN padroniza novamente cada foto e recalcula as coordenadas do bloco.
O P-Net fornece as coordenadas dos blocos e os níveis de confiança (a precisão dessa face) em relação à face que contém para cada bloco. Você pode deixar blocos com um certo nível de confiança usando o parâmetro de limite.
Ao mesmo tempo, não podemos simplesmente selecionar os blocos com o nível máximo de confiança, pois a imagem pode conter vários rostos.
Se um bloco se sobrepõe a outro e cobre quase a mesma área, esse bloco é removido. Este parâmetro pode ser controlado durante a inicialização da rede.

Neste exemplo, o bloco amarelo será removido. Basicamente, o resultado do P-Net são blocos de baixa precisão. O exemplo abaixo mostra os resultados reais do P-Net:

Etapa 3: R-Net
R-Net realiza uma seleção dos blocos mais adequados formados como resultado do trabalho de P-Net, que no grupo é mais provavelmente uma pessoa. R-Net tem uma arquitetura semelhante ao P-Net. Nesse estágio, camadas totalmente conectadas são formadas. A saída de R-Net também é semelhante à saída de P-Net.

Etapa 4: O-Net
A rede O-Net é a última parte da rede MTCNN. Além das duas últimas redes, forma cinco pontos para cada rosto (olhos, nariz, cantos dos lábios). Se esses pontos caírem completamente no bloco, então será determinado como o que provavelmente contém a pessoa. Os pontos adicionais são marcados em azul:

Como resultado, obtemos um bloco final indicando a precisão do fato de que este é um rosto. Se o rosto não for encontrado, obteremos o número zero de blocos de rosto.
Em média, o processamento de 1000 fotos por essa rede leva 6 minutos em nosso servidor.
Temos usado repetidamente essa rede neural em verificações, e ela nos ajudou a identificar automaticamente anomalias entre as fotos de nossos clientes.
Sobre o uso do FaceNet, gostaria de acrescentar que se, em vez de Mona Lisa, você começar a analisar as telas de Rembrandt, o resultado será algo parecido com a imagem abaixo, e você terá que analisar toda a lista de pessoas identificadas:

Conclusão
Essas hipóteses e abordagens de teste demonstram que, com absolutamente qualquer conjunto de dados, você pode realizar testes interessantes e procurar anomalias. Muitos auditores estão agora tentando desenvolver práticas semelhantes, então eu queria mostrar exemplos práticos do uso de visão computacional e aprendizado de máquina.
Também gostaria de acrescentar que consideramos o reconhecimento facial como a próxima hipótese para teste, mas até agora os dados e as especificações do processo não fornecem uma base razoável para o uso dessa tecnologia em nossos testes.
Em geral, isso é tudo o que eu gostaria de dizer sobre nossa maneira de testar fotos.
Desejo-lhe boas análises e dados rotulados!
* O código de amostra é obtido de fontes abertas.