Nós entendemos e criamos
A boa notícia antes do artigo: altas habilidades matemáticas não são necessárias para ler e (com sorte!) Compreender.
Aviso: A parte do código deste artigo, como o anterior , é uma tradução adaptada, complementada e testada. Agradeço ao autor, pois esta é uma das minhas primeiras experiências no código, depois da qual inundei ainda mais. Espero que minha adaptação funcione da mesma forma para você!
Então vamos!
A estrutura é assim:
- O que é uma cadeia de Markov?
- Um exemplo de como a corrente funciona
- Matriz de transição
- Modelo de cadeia de Markov com Python - geração de texto baseada em dados
O que é uma cadeia de Markov?
A cadeia de Markov é uma ferramenta da teoria dos processos aleatórios, consistindo em uma sequência de n números de estados. Nesse caso, as conexões entre os nós (valores) da cadeia são criadas apenas se os estados estiverem estritamente próximos um do outro.
Tendo em mente apenas a palavra do tipo gordura , vamos deduzir a propriedade da cadeia de Markov: A
probabilidade de um certo novo estado na cadeia depende apenas do estado presente e não leva em consideração matematicamente a experiência de estados anteriores => Uma cadeia de Markov é uma cadeia sem memória.
Em outras palavras, um novo significado sempre dança daquele que o segura diretamente pela alça.
Um exemplo de como a corrente funciona
Como o autor do artigo, do qual a implementação do código foi emprestada, vamos pegar uma sequência aleatória de palavras.
Iniciar - artificial - casaco de pele - artificial - comida - artificial - macarrão - artificial - casaco de pele - artificial - fim
Vamos imaginar que este é realmente um grande verso e nossa tarefa é copiar o estilo do autor. (Mas fazer isso, é claro, é antiético)
Como decidir?
A primeira coisa óbvia que quero fazer é contar a frequência das palavras (se fôssemos fazer isso com um texto ativo, primeiro valeria a pena normalizar - trazer cada palavra para um lema (forma de dicionário)).
Início == 1
Artificial == 5
Casaco de pele == 2
Massa == 1
Comida == 1
Fim == 1
Tendo em mente que temos uma cadeia de Markov, podemos traçar a distribuição de novas palavras em função das anteriores graficamente: Em palavras

:
- o estado do casaco de pele, comida e massa 100% implica o estado de p = 1 artificial
- o estado "artificial" pode levar a 4 condições com igual probabilidade, e a probabilidade de chegar ao estado de um casaco de pele artificial é maior do que as outras três
- estado final não leva a lugar nenhum
- o estado "iniciar" 100% implica o estado "artificial"
Parece legal e lógico, mas a beleza visual não termina aí! Também podemos construir uma matriz de transição e, com base nela, podemos apelar com a seguinte justiça matemática:

O que em russo significa "a soma das séries de probabilidades para algum evento k, dependendo de i == a soma de todos os valores das probabilidades do evento k, dependendo da ocorrência do estado i, onde o evento k == m + 1, e evento i == m (ou seja, o evento k sempre difere em um de i) ”.
Mas primeiro, vamos entender o que é uma matriz.
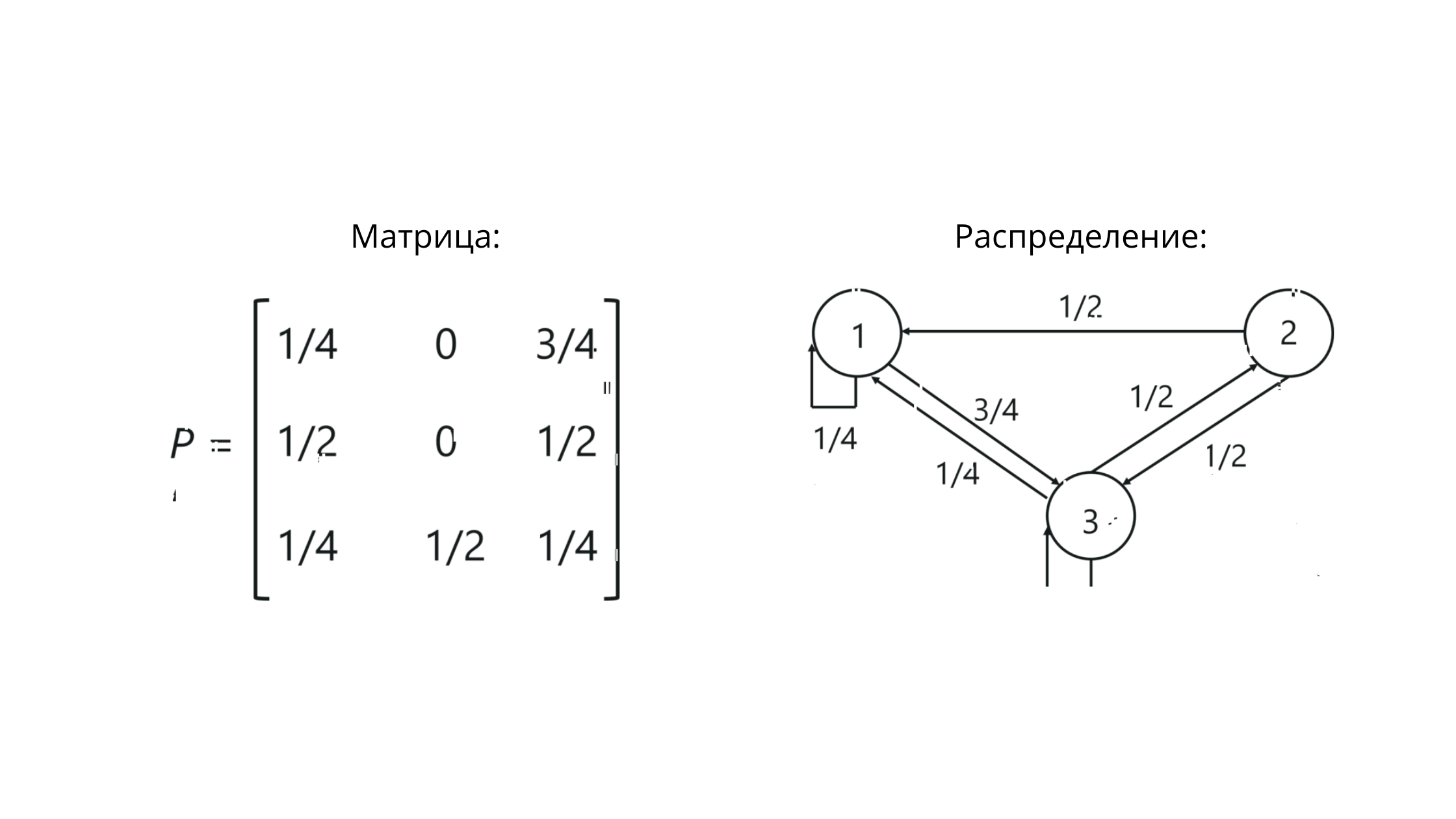
Matriz de transição
Ao trabalhar com cadeias de Markov, estamos lidando com uma matriz de transição estocástica - um conjunto de vetores, dentro dos quais os valores refletem os valores das probabilidades entre gradações.
Sim, sim, parece que sim.
Mas não parece tão assustador:

P é a notação para uma matriz. Os valores na interseção de colunas e linhas aqui refletem as probabilidades de transições entre estados.
Para o nosso exemplo, será mais ou menos assim:

Observe que a soma dos valores na linha == 1. Isso significa que construímos tudo corretamente, porque a soma dos valores na linha da matriz estocástica deve ser igual a um.
Exemplo
simples sem casacos de peles artificiais e pastas: um exemplo nu é a matriz de identidade para:
- o caso em que é impossível voltar de A para B, e de B - de volta para A [1]
- o caso em que a transição de A para B de volta é possível [2]

Respecto. Com a teoria concluída.
Usamos Python.
Um modelo baseado na cadeia de Markov usando Python - gerando texto com base em dados
Etapa 1
Importe o pacote relevante para o trabalho e obtenha os dados.
import numpy as np
data = open('/Users/sad__sabrina/Desktop/1.txt', encoding='utf8').read()
print(data)
, , , , ( « memorylessness »). , , , , , , ; .., , .
Não se concentre na estrutura do texto, mas preste atenção à codificação utf8. Isso é importante para ler os dados.
Etapa 2
Divida os dados em palavras.
ind_words = data.split()
print(ind_words)
['\ufeff', '', '', '', '', ',', '', '', ',', '', '', '', '', '', '', '', ',', '', '', '', ',', '', '', '', '', '(', '', '', '«', 'memorylessness', '»).', '', ',', '', '', '', '', ',', '', '', '', '', '', '', '', ',', '', '', '', '', '', '', '', '', '', ',', '', '', '', '', '', '', '', ',', '', '', ',', '', '', '', ';', '..,', '', '', '', '', ',', '', '', '', '', '', '', '.']Etapa 3
Vamos criar uma função para ligar pares de palavras.
def make_pairs(ind_words):
for i in range(len(ind_words) - 1):
yield (ind_words[i], ind_words[i + 1])
pair = make_pairs(ind_words)A principal nuance da função no uso do operador yield (). Ajuda-nos a cumprir o critério de encadeamento de Markov - o critério de armazenamento sem memória. Com o rendimento, nossa função criará novos pares conforme itera (repetições), em vez de armazenar tudo.
Um mal-entendido pode surgir aqui, porque uma palavra pode se transformar em outras. Vamos resolver isso criando um dicionário para nossa função.
Passo 4
word_dict = {}
for word_1, word_2 in pair:
if word_1 in word_dict.keys():
word_dict[word_1].append(word_2)
else:
word_dict[word_1] = [word_2]Aqui:
- se já tivermos uma entrada sobre a primeira palavra de um par no dicionário, a função adicionará o próximo valor potencial à lista.
- caso contrário: uma nova entrada é criada.
Etapa 5
Vamos escolher aleatoriamente a primeira palavra e, para tornar a palavra realmente aleatória, definir a condição while usando o método de string islower (), que satisfaz True se a string contiver letras minúsculas, permitindo a presença de números ou símbolos.
Nesse caso, definiremos o número de palavras como 20.
first_word = np.random.choice(ind_words)
while first_word.islower():
chain = [first_word]
n_words = 20
first_word = np.random.choice(ind_words)
for i in range(n_words):
chain.append(np.random.choice(word_dict[chain[-1]]))Etapa 6
Vamos começar nossa coisa aleatória!
print(' '.join(chain))
; .., , , (A função join () é uma função para trabalhar com strings. Entre parênteses, especificamos um separador para os valores na linha (espaço).
E o texto ... bem, parece uma máquina e quase lógico.
PS Como você deve ter notado, as cadeias de Markov são úteis em linguística, mas sua aplicação vai além do processamento de linguagem natural. Aqui e aqui você pode se familiarizar com o uso de correntes em outras tarefas.
PPS Se minha prática de código se tornou incompreensível para você, estou anexando o artigo original . Certifique-se de aplicar o código na prática - a sensação de quando ele "funcionou e gerou" é carregar!
Estou aguardando suas opiniões e terei o prazer de receber comentários construtivos sobre o artigo!