Clever Geek Handbook

O paradoxo do aniversário nos dados VK

Olá!



Decidi verificar o paradoxo do aniversário usando dados disponíveis da VK.



Qual é o paradoxo do aniversário?



Tente responder à pergunta: Quantas pessoas em uma sala são necessárias para que duas pessoas tenham o mesmo aniversário com uma probabilidade de 0,5? (data e mês). O paradoxo do aniversário responde a essa pergunta.



Para resolver o problema, vale ressaltar vários pré-requisitos:



  1. O modelo não terá 29 de fevereiro => 365 dias por ano no modelo
  2. Cada um dos 365 dias é igualmente provável.


É claro que não é totalmente realista que aniversários sejam igualmente prováveis ​​- existem efeitos sazonais que afetam as datas de nascimento dos filhos, acho que você pode adivinhar quais ...



A maioria das pessoas responde intuitivamente à pergunta do problema: 180. Parece lógico, são necessárias 180 pessoas para ter probabilidade de 0,5 aniversários idênticos (365 dias no total). Todo mundo que nunca ouviu falar do paradoxo do aniversário é sobre essa intuição. A resposta correta é realmente muito menor que 180, e até 150, e até 100: 23.



É necessário pelo menos 1 aniversário correspondente - para que eu possa encontrar a probabilidade de que não haja aniversários correspondentes:

P(" ")=365∗364∗363∗...∗(365−k+1)365k=365!365k∗(365−k)!

.

A idéia é a seguinte: pego a primeira pessoa e lembro do aniversário dele, depois a segunda e calculo a probabilidade de que o aniversário dele não coincida com o aniversário da primeira; além do terceiro e calculo a probabilidade de seu aniversário não coincidir com os aniversários do primeiro e do segundo.



Resolvendo a equação, são necessárias 23 pessoas e a probabilidade de aniversários coincidentes será de 0,5073, com 100 pessoas, a probabilidade é de 0,9999.



Vamos ver o paradoxo nos dados VK?



Em teoria, com 23 pessoas, a probabilidade de aniversários coincidentes é de 0,5073, com 50 pessoas, 0,97 e com 100, 0,99. Vamos verificar através da API VK.



1. Eu escolho uma grande comunidade no VK. Decidi usar o grupo MDK no Vkontakte ...



Primeiro, crio um arquivo csv com as colunas necessárias. 



with open('vk_data.csv', 'w') as new_file:
                # csv
                fieldnames = ['id', 'bdate', 'bmonth', 'byear', 'dandm']

                csv_writer = csv.DictWriter(new_file, fieldnames=fieldnames, delimiter=',')

                csv_writer.writeheader()

                newDict = dict()


Faço login no VK por meio da API e defino o público que preciso 

vk_session = vk_api.VkApi('username', 'password')
                vk_session.auth()

                vk = vk_session.get_api()
                
                vk_group = vk.groups.getMembers(group_id = 'mudakoff', fields = 'bdate')


Começamos a analisar o VKontakte, a API deles permite analisar apenas 1000 usuários, por isso crio um loop. 



for i in range(0, 20):
                    vk_group = vk.groups.getMembers(group_id = 'mudakoff', offset = 1000 * i,  fields = 'bdate')
                    for k in range(0, 1000):
                        try:
                            new_file.write(str(vk_group['items'][k]["id"]) + ',' + str(vk_group['items'][k]["bdate"]).replace('.', ','))
                            new_file.write('\n')
                        except:
                            pass


Em teoria, assumimos que aniversários são igualmente prováveis, mas o que acontece na prática? Vou construir um histograma de aniversários.



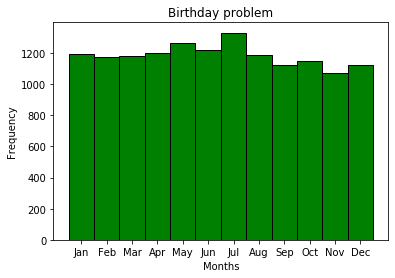
imagem



Aniversários por mês não são eventos equivalentes, o que geralmente é bastante lógico - este é apenas um pré-requisito para resolver o problema do aniversário. Obviamente, haverá diferentes eventos sazonais, para diferentes locais. Por alguma razão, julho é o mês mais popular para o aniversário dos assinantes do MDK.



Estimularemos empiricamente a probabilidade de que em um grupo de 50 pessoas arbitrárias haja pelo menos duas com o mesmo aniversário. Para fazer isso, escrevi um ciclo durante o qual ocorre uma subamostra de 50 linhas da tabela. Para essas 50 linhas dentro da condição, verifiquei a correspondência de aniversários. Se correspondeu, lembrei-o na variável counter, que dividirei posteriormente pela duração do ciclo para obter a probabilidade. 



fifty = df["dandm"].sample(n = 50)
for i in range(0, 1000):
    fifty = df["dandm"].sample(n = 50)
    for j in fifty.duplicated():
        if j == True:
            counter = counter + 1
            break
print(':', counter / 1000)


A probabilidade é obtida na região de 0,97, que coincide com os dados teóricos.



Resultado



Foi interessante ver como a teoria se relaciona com o empirismo e, neste caso, os dados confirmam a teoria. Note-se que o resultado é representativo, pois a amostra é grande o suficiente - 20.000 pessoas.



Recursos



  1. Universidade de Harvard. Problema de aniversário, propriedades da probabilidade | Estatísticas 110. URL: www.youtube.com/watch?v=LZ5Wergp_PA&t=150s . Acesso em: 07/08/2020
  2. Problema de aniversário. URL: en.wikipedia.org/wiki/Birthday_problem . Acesso em: 07/08/2020>


More articles:


All Articles