
Muito Obrigado. Peço desculpas por sentar aqui. Eu sou um homem muito velho.
Meu tópico hoje é, de certo modo, muito especial, porque é muito antigo. Kinks são parte integrante da vida humana, estão sempre lá. Os antigos escreveram sobre isso. Essa coisa está fora de controle. E, em certo sentido, eles parecem ser um grau extremo de complicação - apenas uma bagunça completa.
Existem muitos tipos de desordem. Assim, por pura coincidência, há muitos anos, comecei a lidar com essa forma de complicação e, para minha completa surpresa, encontrei sinais e, devo dizer, sinais muito claros de ordem nas dobras. Hoje, hoje, gostaria de apresentar alguns exemplos do que isso significa. Prefiro a palavra “quebrado” a “desigual” porque, para alguém que estudou latim, como eu na minha juventude distante, a desigualdade é o oposto da igualdade. Mas esse não é o caso.
A igualdade é o oposto da fratura, porque o mundo na maioria das vezes nos parece cheio de fraturas.
Deixe-me mostrar alguns objetos. Alguns deles são criados artificialmente. Outros são muito reais, em certo sentido. Essa é a coisa real.

Isso é couve-flor. Por que estou lhe mostrando couve-flor, uma planta comum e antiga? Porque, apesar de sua rotina e antiguidade, é complexo e simples. é complexo e simples. Por exemplo, não é difícil pesá-lo. O peso importa se vamos comê-lo. Mas suponha que vamos medir sua superfície. Isso está ficando interessante. Depois de cortar uma das flores da couve-flor com uma faca afiada, e olhando de perto, vemos a couve-flor inteira, apenas de tamanho menor. Então você pode cortar novamente e novamente e novamente e novamente e novamente ... E você obtém amostras cada vez menores de couve-flor. A experiência humana mostrou que existem formas com uma propriedade tão interessante que cada parte é semelhante ao todo, mas de tamanho menor. E o que a pessoa aprendeu com esse fato? Muito pouco.
Em conexão com o estudo desse problema, descobri algo completamente surpreendente: a torção pode ser medida por um número, digamos, 2,3 ou 1,2 e, às vezes, muito mais. Um dia, um amigo meu trouxe uma fotografia e, meio de brincadeira, perguntou: "Qual é a dobra dessa curva?" Eu disse: "Pouco menos de um ano e meio". Como se viu, era igual a 1,48. Não demorou muito tempo para eu estudar essas coisas por tanto tempo. Os números em questão indicam o grau de fratura da superfície.

Deixe-me fazer uma reserva imediatamente de que as superfícies são absolutamente artificiais e foram criadas em um computador. O único ponto de partida foi o número. Esse número é torcido. A fratura à esquerda é o resultado da cópia de várias paisagens. À direita - eu me ajeitei mais. Se você olhar de perto, depois de um tempo poderá reconhecer as diferenças nesses dois casos a olho nu.
O homem teve que se acostumar com o conceito de fratura. Isso está muito quebrado, mas isso, pode-se dizer, é suave, mas é completamente suave. Poucas coisas são muito suaves. Vamos agora nos perguntar: qual é a superfície da couve-flor? Pode ser medido e medido e medido ... Quanto mais precisa a medição, maior a superfície e assim por diante, até distâncias muito pequenas. Qual é a extensão da costa desses lagos? Quanto mais precisa for a medida, mais tempo ela ficará. O conceito de comprimento da costa, que parece tão óbvio porque é frequentemente citado, é de fato completamente errado: simplesmente não existe tal coisa. Deve haver uma abordagem diferente.
E qual é a utilidade desse conhecimento? Surpreendentemente, há muitos benefícios. Para começar, as paisagens artificiais que eu, digamos, inventamos, são constantemente usadas na cinematografia. Vemos montanhas ao longe. Pode ser montanhas, mas pode muito bem ser apenas fórmulas fluidas. Isso é muito fácil de conseguir. Costumava demorar muito tempo, mas agora é apenas um pouco. Dê uma olhada aqui. Isso é luz de verdade.
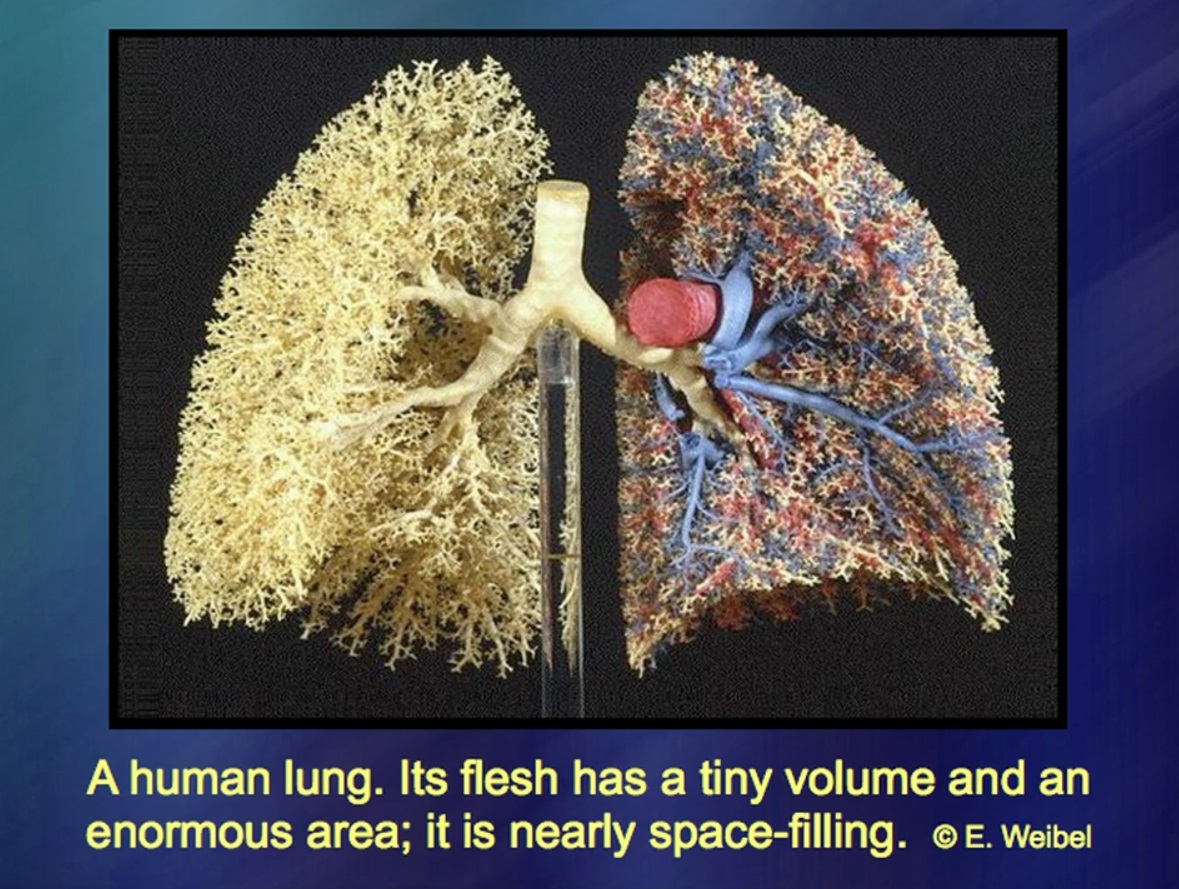
O pulmão é um objeto muito estranho. Todos sabemos muito bem que tem algum peso. Sabe-se também que o volume do pulmão é muito pequeno. E a área do pulmão? Os anatomistas há muito debatem essa questão. Acredita-se que em um homem normal, a área do pulmão é igual à área de uma bola de basquete. Outros argumentam que não existem cinco dessas bolas. As discrepâncias são colossais. Por quê? Porque a área do pulmão é um conceito muito vagamente definido. Os brônquios se ramificam e se ramificam cada vez mais fundo. E eles param de se ramificar não por causa de algum princípio, mas por causa de condições puramente físicas, por causa de muco dentro do pulmão. É assim que um pulmão muito maior é formado: os brônquios se ramificam cada vez mais profundamente, enquanto o espaço entre eles é aproximadamente o mesmo para uma baleia, para uma pessoa e para um pequeno roedor.
Então, qual é a utilidade disso? Surpreendentemente e até surpreendentemente, os anatomistas tinham uma idéia pobre da estrutura do pulmão até recentemente. Acho que minha pesquisa matemática, surpreendentemente, foi de grande ajuda para cirurgiões que estudam doenças pulmonares, bem como doenças hepáticas, onde existem sistemas de filiais com falta de geometria inteligível. Em outras palavras, eu tive que criar geometria para algo que não tem sua própria geometria. Uma qualidade surpreendente foi encontrada: muitas vezes as regras dessa geometria são extremamente concisas. Você começa com fórmulas curtas, aplica-as várias vezes, às vezes repetidamente, repetidamente. A mesma repetição. E, no final, acontece algo assim.
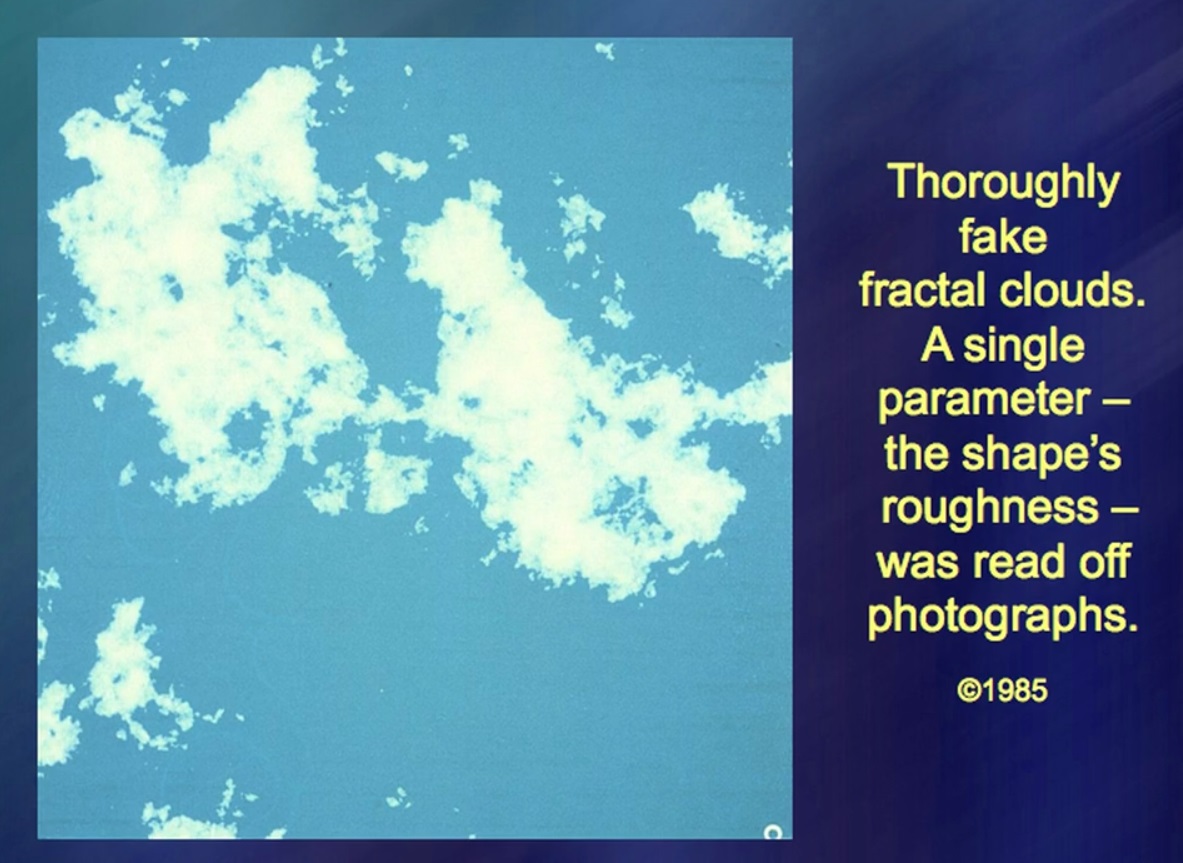
Essa nuvem é completamente artificial, 100%. Ok, 99,9%. O único elemento natural aqui é o número, a fratura da nuvem - esse número é retirado da natureza. Uma coisa tão complexa como uma nuvem, tão instável, mutável, obedece a uma regra simples. Esta regra simples não é uma explicação para a nebulosidade. Mas o mar de nuvens deve levar em consideração essa regra. Não sei o quão perfeitas são essas fotos antigas. Fiz isso intensivamente, mas depois minha atenção foi direcionada para outros fenômenos.
E aqui está mais uma coisa interessante. Um dos eventos revolucionários da história da matemática, insuficientemente apreciado por muitos, ocorreu cerca de 130 anos atrás, 145 anos atrás. Os matemáticos começaram a criar formas inexistentes. Entre os matemáticos, a capacidade de uma pessoa de criar algo que nunca existiu na natureza passou a ser apreciada e em um nível absolutamente inimaginável. Em particular, eles foram capazes de inventar uma curva que preenche todo o plano até o último ponto. Uma curva é uma curva, um plano é um plano e os dois não se encaixam. Acabou que eles se encaixam.
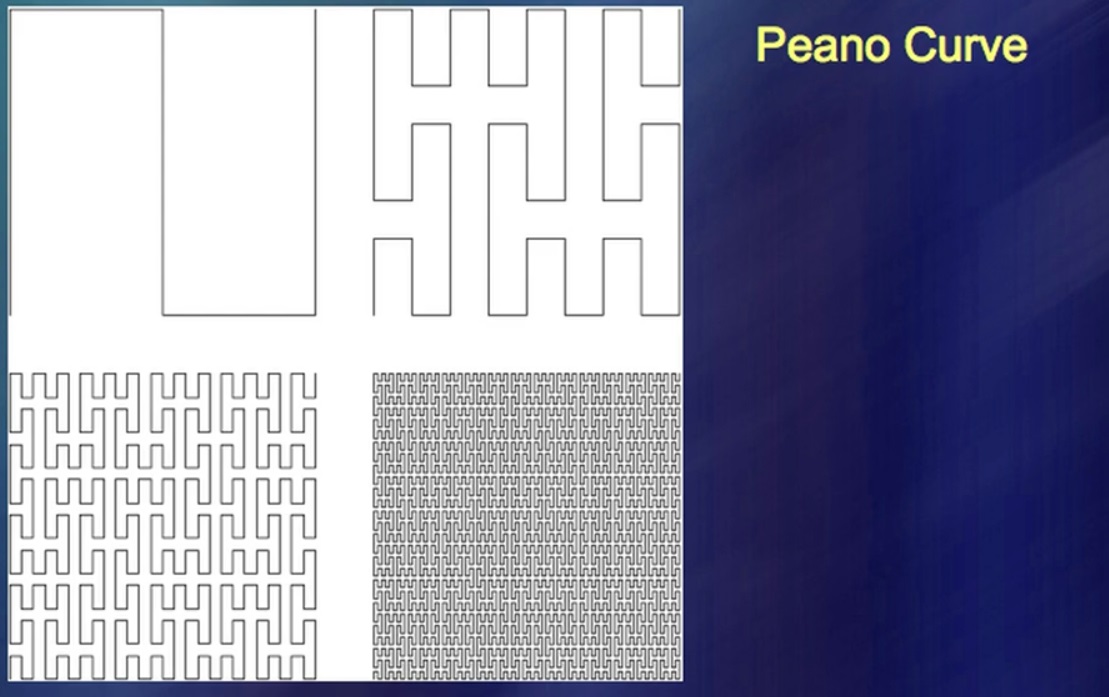
Um homem chamado Peano identificou essas curvas e elas geraram um interesse excepcional. Eles são muito importantes e despertam interesse em grande parte porque houve algum tipo de divisão da matemática em uma baseada na realidade e outra que vem da pura razão. Infelizmente, acabei provando que o que se tornou conhecido pelos esforços da pura razão, de fato, é conhecido há muito tempo de uma forma diferente. Aqui eu tenho um sistema de riachos em forma de curvas preenchendo o avião.

Em si, isso é história. Foi entre 1875 e 1925, um período incrível em que a matemática se preparava para romper com o mundo real. Certos objetos serviram como ilustração da lacuna, desde a minha infância e meus anos de estudante, a lacuna entre a matemática e a realidade visível. No entanto, consegui repensá-los, virar de cabeça para baixo e, com a ajuda deles, descrever alguns aspectos da complexidade da natureza.
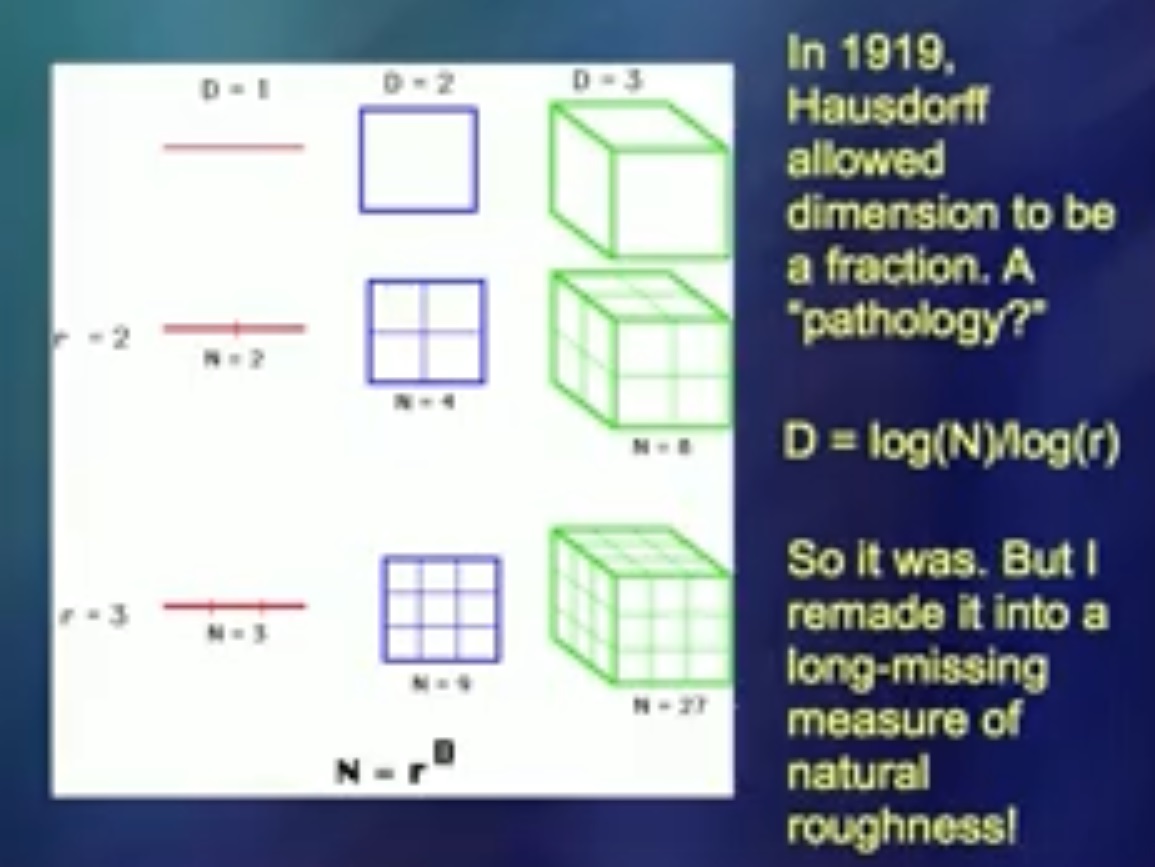
Em 1919, um homem chamado Hausdorff identificou um número que poderia ser considerado uma piada matemática. Mas descobri que esse número é uma boa ferramenta para medir torções. Quando contei a meus colegas sobre isso, eles disseram: “Não seja bobo. Isso é alguma coisa ... ”Na verdade, eu não estava fazendo coisas estúpidas.

O grande artista Hokusai sabia disso muito bem. Na parte inferior da imagem estão as algas. Hokusai não conhecia a matemática necessária: simplesmente não existia na época. Além disso, sendo japonês, ele [na época] não tinha contato com o Ocidente. Mas a arte há muito tempo contém elementos fractais. Eu posso falar sobre isso por um longo tempo.

A Torre Eiffel tem elementos fractal. Eu li o livro de Eiffel sobre sua torre - o alcance de seu entendimento é incrível.
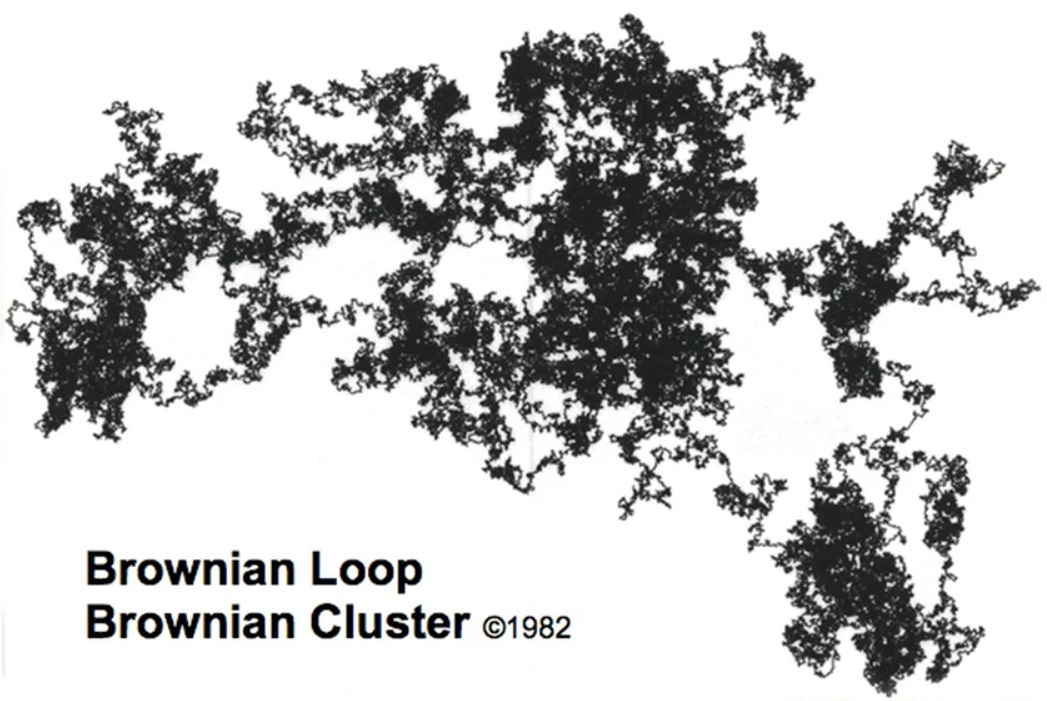
Aqui está uma bagunça dentro de uma bagunça. Laço browniano. Uma vez decidi que havia passado uma parte considerável da minha vida profissional, e tantas coisas diferentes me ocuparam que decidi que era hora de me testar. Posso explorar um objeto que todo mundo está explorando há muito tempo e encontrar algo radicalmente novo nele? Comecei a estudar tudo o que se enquadra na categoria de movimento browniano. Tentei ângulos diferentes, tentei métodos diferentes e voltei para onde comecei. Então sugeri ao meu assistente: “Não vejo nada aqui. Você pode pintar? " Ele fez isso, ou seja, ele preencheu todo o interior. "Eu consegui…"

Mas gritei: “Pare! Pare! Pare! Entendido: esta é uma ilha. " Surpreendente. O movimento browniano tem uma torção igual a dois. Eu medi-lo, verifica-se 1,33. Eu meço de novo e de novo. Medições longas, grandes movimentos brownianos. Novamente: 1,33. Um problema matemático surge imediatamente: como provar isso? Meus amigos levaram 20 anos. Três tinham evidências incompletas. Eles uniram forças e juntos conseguiram obter provas. Como resultado, eles receberam a famosa medalha [Fields] para matemáticos. No geral, os matemáticos receberam três medalhas [Fields] por provar fatos que eu vi, mas não pude provar.
Agora as pessoas me perguntam em todos os lugares: “Como tudo começou? Como seus estudos o levaram a coisas tão incomuns? "
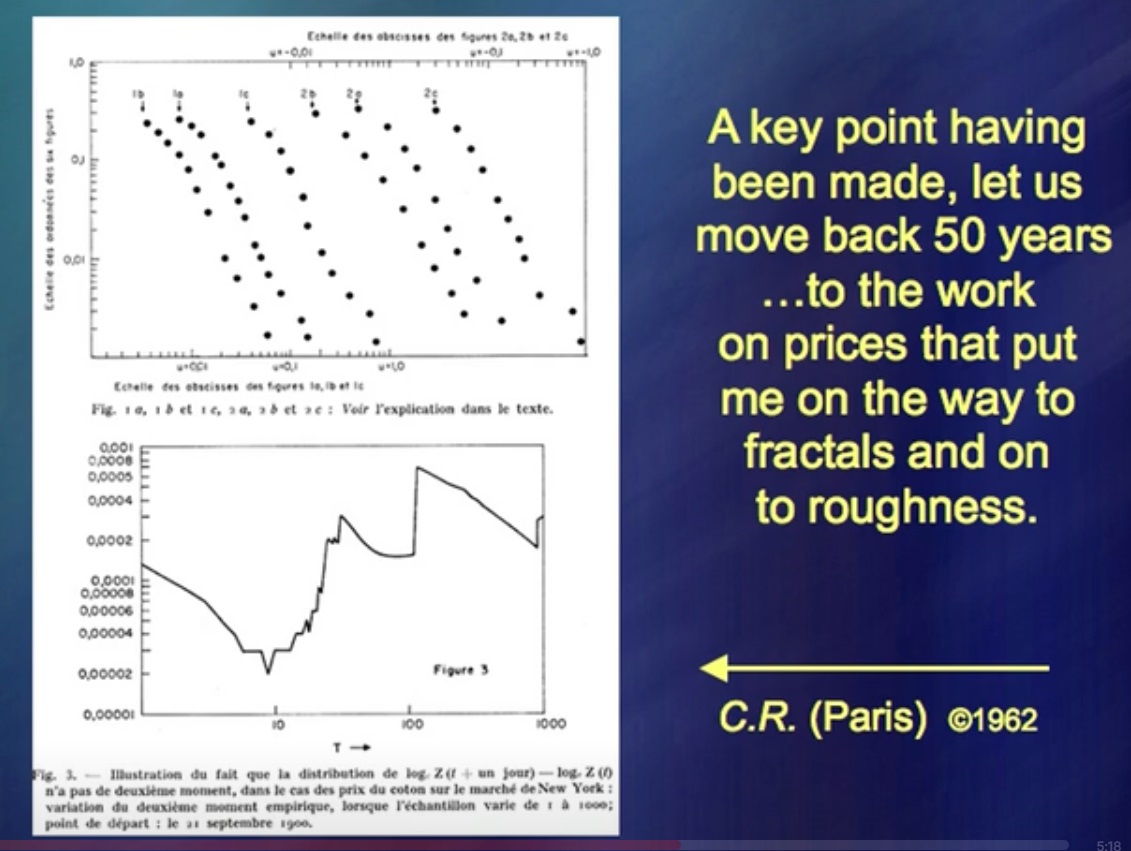
O que me permitiu ser simultaneamente engenheiro mecânico, geógrafo, matemático etc.? Curiosamente, mas comecei estudando os preços na bolsa.

Eu tinha uma teoria e escrevi livros sobre ela.
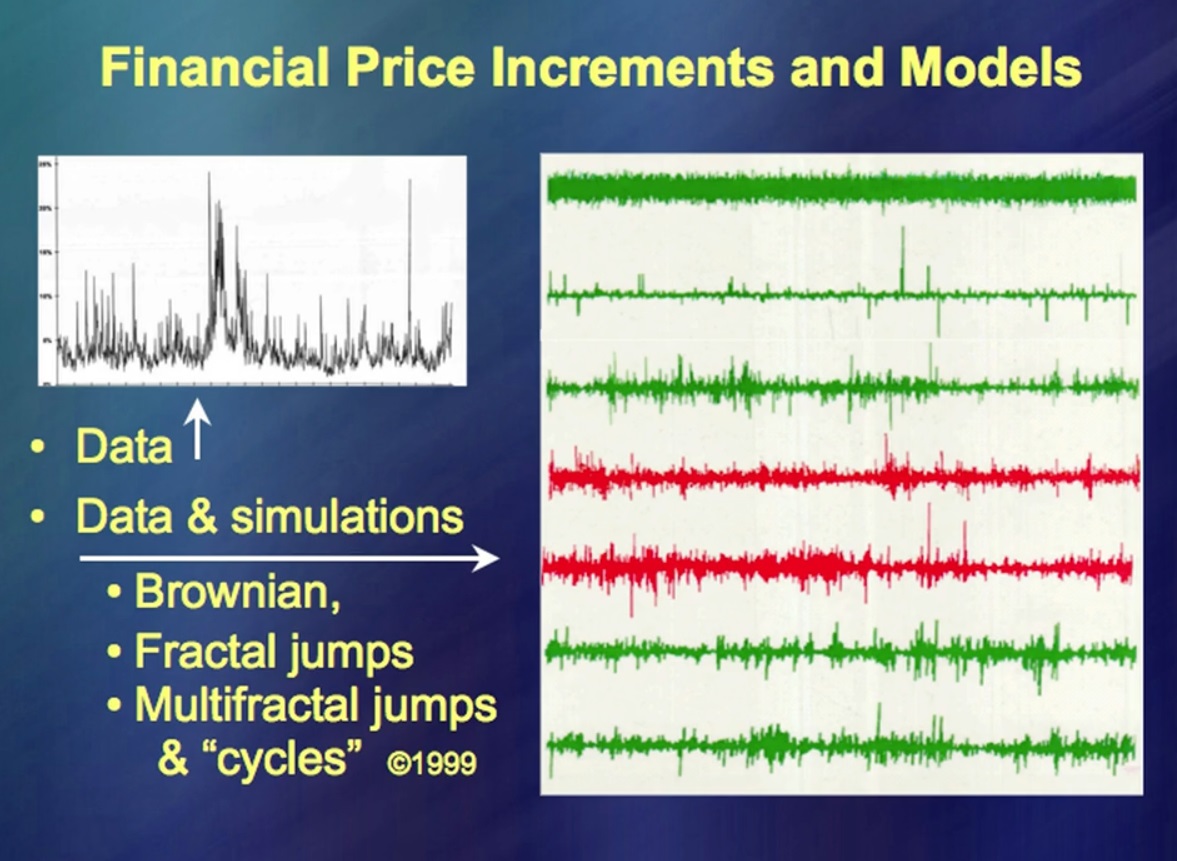
"Movimentos de preços de instrumentos financeiros" À esquerda, você pode ver os dados por um longo período, à direita, no topo - os dados de acordo com uma teoria muito, muito na moda. É extremamente simples e você pode escrever muitos livros sobre isso muito rapidamente. (Risos) Existem milhares de livros sobre esse assunto. Agora compare com movimentos reais de preços. E onde eles estão? Linhas adicionais incluem movimentos reais de preços, bem como uma pequena farsa da minha parte. A idéia principal era que você precisa ser capaz de fazer ... Como é chamado? … Simulação de flutuações de preços. Isso funcionou muito bem há 50 anos.
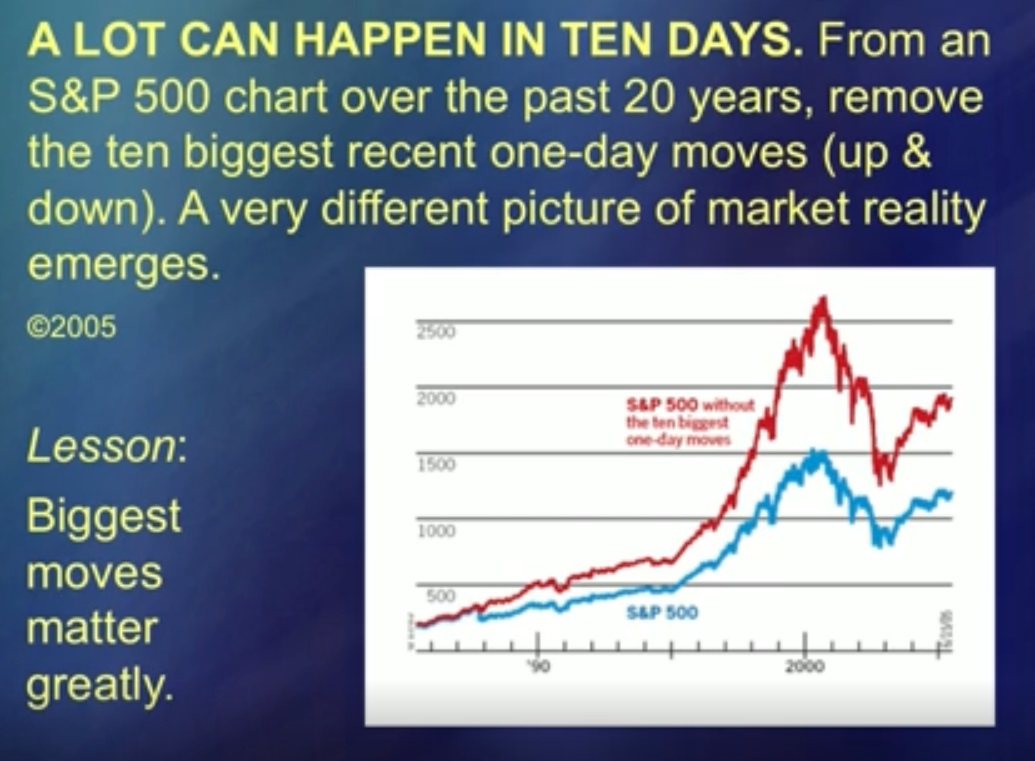
Por 50 anos, minha ideia foi ridicularizada porque poderia ter sido mais fácil. Mas agora, eu lhe digo, eles começaram a me ouvir. (Risos) Essas duas curvas representam médias. Azul é o Standard and Poor's [S&P 500] e vermelho é o Standard and Poor's, do qual os cinco maiores picos de preços foram subtraídos. O salto certamente estraga a análise e, em muitos estudos, é considerado [não analítico] um caso especial. “Incrível coincidência, intervenção do Senhor. Bem, uma coisinha, você pode simplesmente deixar de lado ". As intervenções do Senhor neste gráfico, e há exatamente cinco delas, como se vê, são tão importantes quanto todo o resto. Em outras palavras, as intervenções do Senhor não podem ser deixadas de lado.
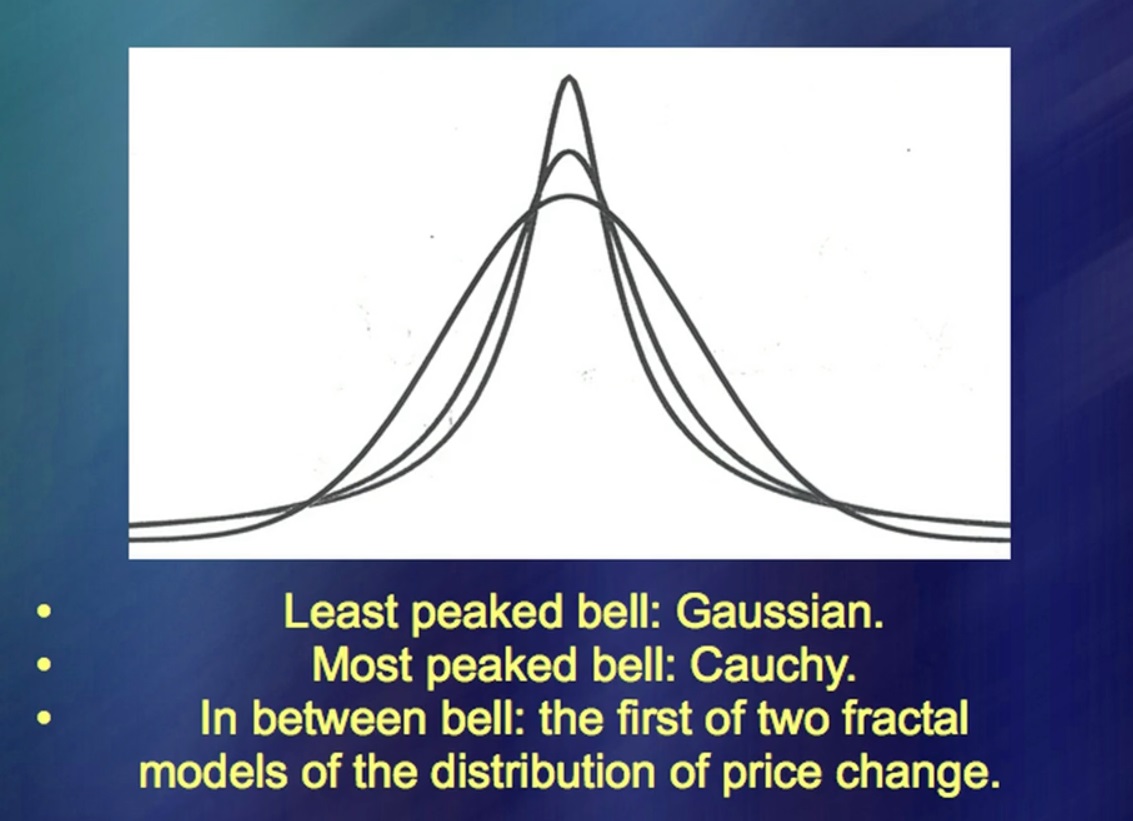
É um ser, é o próprio objeto de análise. Se você lida com eles, também pode lidar com movimentos de preços. Mas eu não descobri os saltos, então você pode analisar o chamado ruído o quanto quiser, mas essa análise não fará sentido. Essas curvas mostram o impacto.

Agora voltarei ao último tópico - o conjunto que recebeu o meu nome. De certa forma, esta é a história da minha vida. Minha adolescência foi na França, que foi ocupada pela Alemanha naqueles anos. Desde que pensei que a qualquer momento não estivesse, tive grandes sonhos. Depois da guerra, encontrei meu tio novamente. Meu tio era um matemático notável e disse: “Aqui está um problema para você. 25 anos atrás, eu não conseguia resolver, e ninguém pode resolver. Esta é a construção de um matemático chamado Gaston Julia e outro chamado Pierre Fatou. Se você puder encontrar algo novo aqui - qualquer coisa - considere que sua carreira está segura. " Muito simples. Comecei a estudar esse problema e, como milhares de pessoas que tentaram fazer isso antes de mim, não conseguiram nada.
Mas então os computadores apareceram. E decidi que precisava aplicar o poder da computação não a novos problemas matemáticos - como, por exemplo, essa coisa curvilínea: esse é um problema novo - mas a problemas antigos. E mudei dos chamados números reais, ou seja, de pontos em uma linha reta a números complexos, e esses são pontos em um plano, ou seja, o que é necessário neste problema. O resultado é esse número.

Este é de complexidade excepcional. A equação está oculta: z se transforma em z ^ 2 + c. Tão simples e chato, tão desinteressante. Agora vamos executá-lo uma vez, duas vezes ... Duas vezes é suficiente. Sobre um milagre! É isso que aparece. Não vou explicar essas coisas aqui, mas acontece que é isso que é isso.


Figuras de tal complexidade, harmonia e beleza são obtidas repetidamente, repetidas vezes. Minha principal descoberta foi que essas ilhas têm a mesma forma, mais ou menos, que toda a figura. O resultado são joias barrocas tão impressionantes.

E toda essa fórmula curta, na qual há tudo - quanto existe? - cinco ícones. E este é o resultado.

A cor foi adicionada por dois motivos. Primeiro, porque os números são tão complexos que é difícil ver o significado dos números. E você precisa escolher algum tipo de sistema para refleti-los no avião. Por isso, tomei como princípio representar sempre as figuras em cores diferentes: uma cor significa uma coisa e outra significa outra, etc. Isso é tão difícil.
Em 1990, eu estava no Reino Unido, em Cambridge, onde recebi um prêmio da universidade. Três dias depois, um piloto, voando sobre o campo, viu isso.

De onde viria tal coisa? Claro - dos alienígenas.
Um dos jornais de Cambridge publicou um artigo sobre essa "descoberta" e, no dia seguinte, recebeu 5.000 cartas, dizendo que este é o conjunto de Mandelbrot, apenas muito grande.

Me deixe terminar. Esta imagem é obtida através da matemática pura. Regras simples podem criar um milagre sem fundo se repetidas sem parar.
Traduzido por Namik Kasumov
Avaliado por Ekaterina Tsvetkova

Descubra os detalhes de como obter uma profissão de alto nível do zero ou subir de nível em habilidades e salário fazendo os cursos on-line pagos do SkillFactory:
- Machine Learning (12 )
- Data Science (12 )
- (9 )
- «Python -» (9 )