Este artigo descreve em palavras simples os criptoalgoritmos que são atualmente padrões de segurança da informação russos relevantes e links selecionados para materiais que, se desejado, ajudarão a entendê-los mais profundamente. E também, ao final do artigo, são dados trabalhos com os resultados da criptanálise de um dos elementos mais importantes desses algoritmos.
De notícias
. , .

2020 « — , », . , . , 2024 , .
, - eSim.
, .
, .
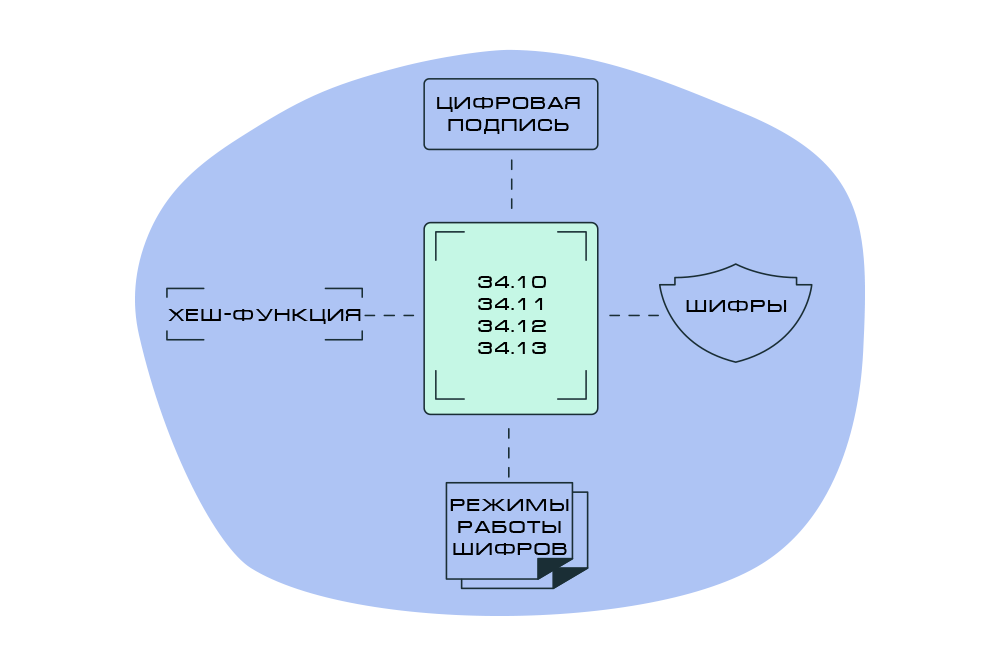
34.10-2018 . 256 512 .
, . , , . , , , .
, , , .
,
,
,
, ( )
,
,
.
, . .
,
, ,
,
,
.
,
.
, , .
.
.

:
.
— -() - , , - — .
— ,
— , -
.
,
1.
— , .
— .
— , .
.
.
— ,
.
,
0, .
: .
.
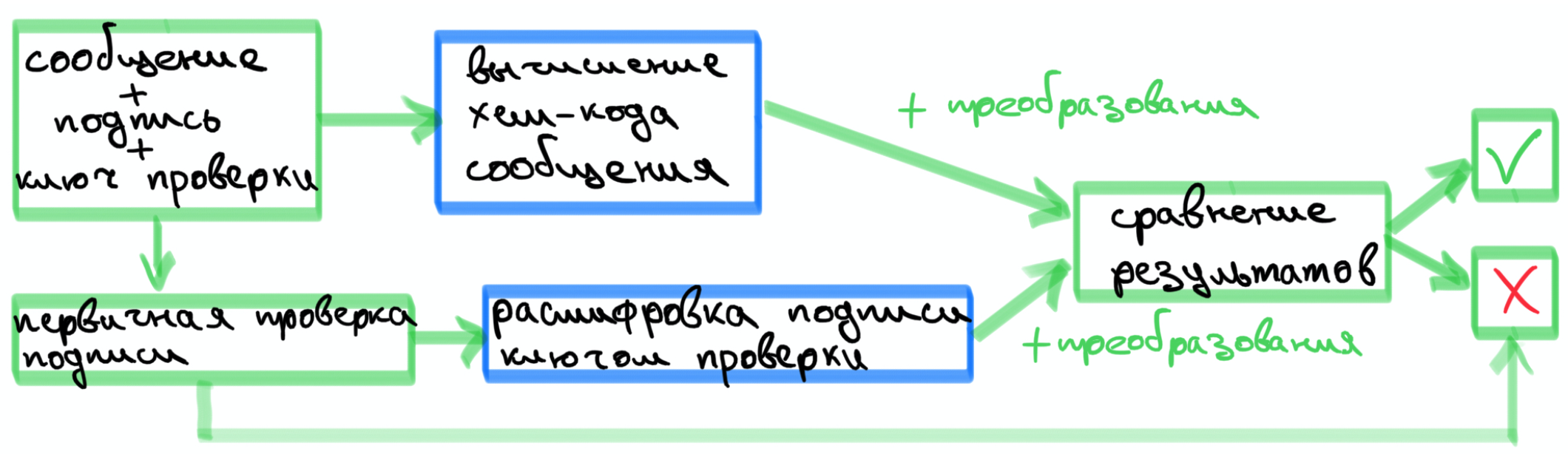
: c
— , , , .
— - , .
— ,
, -
.
,
1.
.
— ,
.
— ,
: /
-
34.11-2018 . -, , .
, 512 ( ). - 256 512 .
@NeverWalkAloner.
34.12-2018 . — 128 64 256 .
10 , , ( ).
.

, , .
@sevastyan01 .
32 , , .
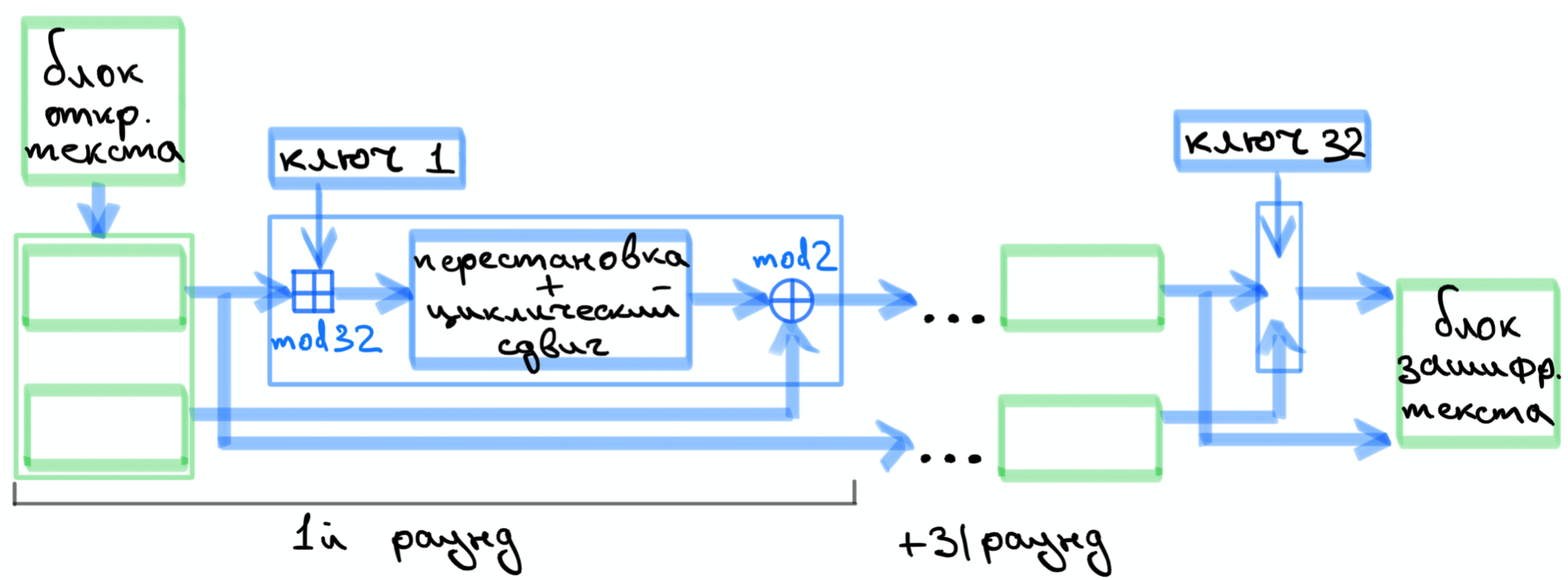
, .
34.13-2018 .
. , , . , .

. , .

2, XOR. , , .
, .
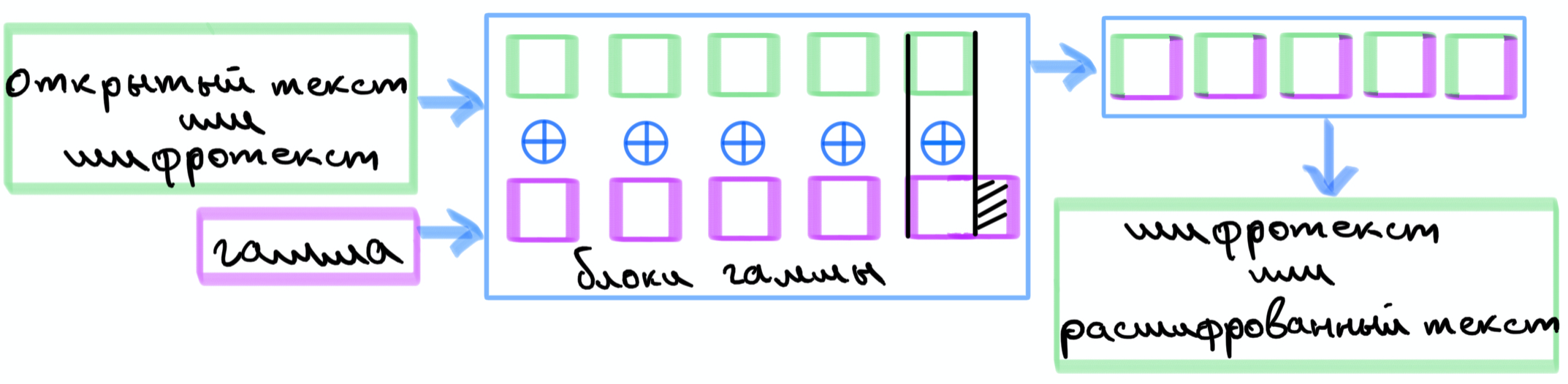
, . .
: ,
, . , , .
.

. , , . .
, , , .
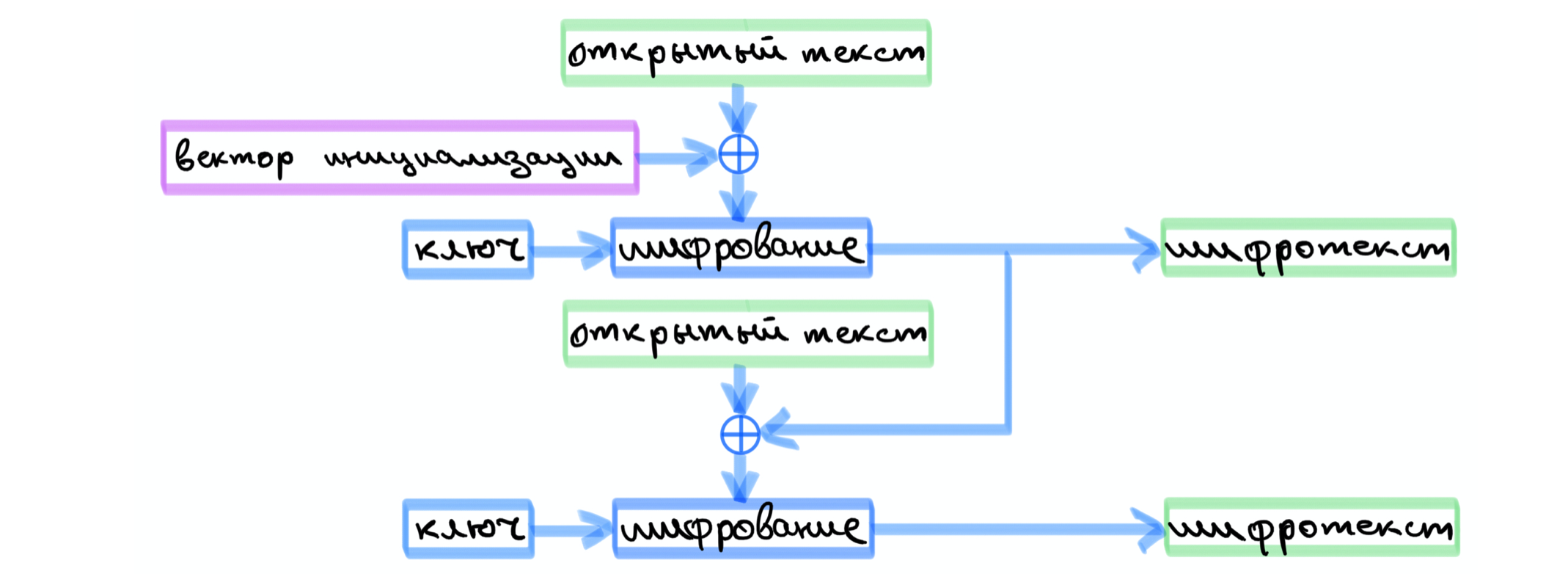
, .
1 2019 . , .
@ru_crypt .
34.10-2018. - , 34.11-2018.
34.12-2018.
. 34.11-2018, .
, . .
, . , .
:
Reverse-Engineering the S-Box of Streebog, Kuznyechik and STRIBOBr1 — Alex Biryukov, L ́eo Perrin, and Aleksei Udovenko
Exponential S-Boxes: a Link Between the S-Boxes of BelT and Kuznyechik/Streebog — Léo Perrin and Aleksei Udovenko
Partitions in the S-Box of Streebog and Kuznyechik — Léo Perrin
, SageMath.
, . , .