Para diluir a furiosa matemática das palestras " Controle em sistemas técnicos " de Oleg Stepanovich Kozlov , publicamos aqui um exemplo de aplicação prática do conhecimento dessas palestras.

Neste artigo, Alexander Shchekaturov, aluno de Oleg Stepanovich, descreve a criação de um modelo de um octocóptero, ao longo do caminho revelando os segredos e demonstrando as técnicas de trabalho em ambiente de modelagem estrutural de sistemas físicos.

Este artigo fornece uma descrição de um logicamente concluído, mas apenas uma parte do trabalho completo de modelagem, mas esta parte é suficiente para uma introdução ao tópico de modelagem dinâmica de um UAV do tipo drone.

, , : , . ( ), , , — , , , / , , .. .., — .

1

: 10…25 , 4, 6 8- (), , , 8, 12 16 T-motors Antigravity 6007 KV320 ( 2 50% ). .

: , , .

2

, - . , — ( , , ). [1] [2].

, ( ), , :

1. ( ) , , – () . , - . ( , 0), :

   $$FM(t)=CT⋅ω2(t),MM(t)=CQ⋅ω2(t),

   
   
   , ( ):
   
   $$CT=2.02268⋅10−4H⋅c2,
   
   $$MM≈0  ⋅⋅2 — ,
   
   $$ω(t) – , /.
2. () , , , . (4 , 4 ) . , - – , . , $$FM(t) [], , , . , , ( ) .
3. : ) , ) , . I B ( inertial – body – ). : $$xI-, $$yI- , $$zI-, $$xB — , $$yB- , $$zB- (. ):
   
   
   
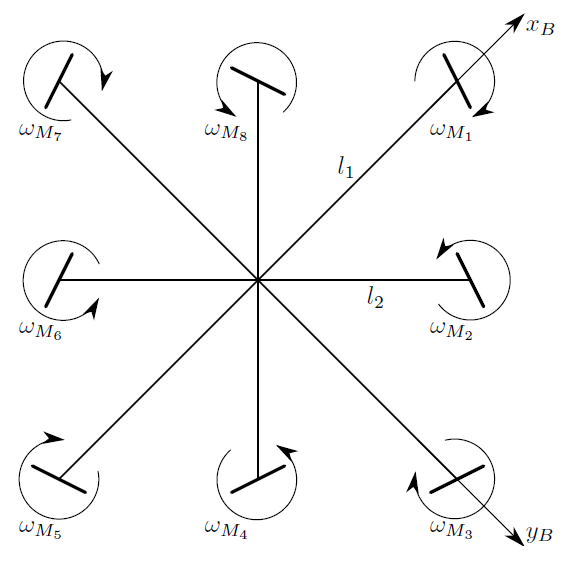
   , B :
   
   

   $$→rM1=(l1,0,0)T,    →rM2=1√2(l2,l2,0)T→rM3=(0,l1,0)T,    →rM4=1√2(−l2,l2,0)T→rM5=(l1,0,0)T,    →rM6=1√2(−l2,−l2,0)T→rM7=(0,−l1,0)T,    →rM8=1√2(l2,−l2,0)T

   
   
   $$l1 – 1, 3, 4 5- , $$l2 – 2, 4, 6 8- .
   
   

   ( ) , , ( 1…5 , – ). $$γ, :
   
   

   $$→eM1=(0,−sin(γ),−cos(γ))T,   →eM2=(−sin(γ)√2,sin(γ)√2,−cos(γ))T,→eM3=(sin(γ),0,−cos(γ))T,   →eM4=(−sin(γ)√2,−sin(γ)√2,−cos(γ))T,→eM5=(0,sin(γ),−cos(γ))T,   →eM6=(sin(γ)√2,−sin(γ)√2,−cos(γ))T,→eM7=(−sin(γ),0,−cos(γ))T,   →eM8=(sin(γ)√2,sin(γ)√2,−cos(γ))T.

   
   
   (, B, ) , . , , .
   
   [1].
4. , . :
   
   
   
   4.1) . $$zI. – , . ( , , ).
   
   
   
   4.2) – 8, , .
   
   
   
   4.3) (/ ) – . , ( ). – , « » ( ).
   
   
   
   4.4) – . .
   
   
5. , :
   
   
   
   5.1) . , - – . .
   
   
   
   5.2) – , .
   
   
   
   5.3) – , , .
   
   
   
   5.4) .
   
   
   
   5.5) – .
   
   
   
   5.6) Momentos das forças de empuxo do VMG. Como as hélices não estão localizadas no centro de gravidade do helicóptero, cada hélice gerará seu próprio momento de giro. Este é talvez o principal fator que rege a orientação da aeronave no espaço.

3 equações não lineares da dinâmica do octocóptero

Levando em consideração as suposições feitas e o fato de que o helicóptero é modelado como um único corpo rígido, a base do modelo de dinâmica do helicóptero é muito simples - esta é a segunda lei de Newton, que em forma vetorial se parece com isto, existem apenas duas equações simples:

$$d→p(t)dt=→F(t),d→eu(t)dt=→M(t),

Onde $$→p(t))=m⋅→v(t)É o impulso do helicóptero, e $$→eu(t)=Eu(t)⋅→ω(t) - o momento angular do helicóptero, $$m - sua massa, $$Eu(t) - tensor de inércia (operador linear do momento de inércia). $$→F(t) e $$→M(t) a essência da soma de todas as forças e todos os momentos atuando no helicóptero.

, , , ( ). - , - , , , , . – , , B, , ( ) . [1], .

Substituindo os valores para o momento e momento angular do helicóptero nas equações dadas da segunda lei de Newton, para o sistema de coordenadas inercial, obtemos:

$$d→vEu(t)dt=1m→FEu(t),d→ωEu(t)dt=Eu-1(→MEu(t)-dEuEudt⋅→ωEu)...

Nessas equações, os lados direitos são muito matematicamente complexos e as equações de dinâmica no sistema de coordenadas associado B (onde os lados direitos são mais simples) não podem ser obtidas tão facilmente, uma vez que o sistema de coordenadas associado ao helicóptero gira.

– . , – . . : φ (roll), θ (pitch) / ψ (yaw), I B $$RIB $$RBI=RTIB, I, B, , , : $$→FI(t)=RBI→FB(t), $$→FB(t)=RIB→FI(t).

, : I , , B. , , $$→F(t) ( ), . – . – , , . , , . .

- , , , B. , $$→ωB(t) $$→vB(t), ( – ) I , , .

I B, cos() = c() sin() = s():

$$RIB==(c(θ)⋅s(ψ)c(θ)⋅s(ψ)−s(θ)s(φ)⋅s(θ)⋅c(ψ)−c(φ)⋅s(ψ)s(φ)⋅s(θ)⋅s(ψ)+c(φ)⋅C(ψ)s(φ)⋅c(θ)c(φ)⋅s(θ)⋅c(ψ)+s(φ)⋅s(ψ)s(φ)⋅s(θ)⋅s(ψ)−s(φ)⋅c(ψ)c(φ)⋅c(θ))

Observe novamente que a cada momento esta matriz será obviamente diferente, uma vez que os ângulos de orientação da mudança de helicóptero. Mas esses são apenas cálculos algébricos, sem quaisquer equações diferenciais. A própria matriz não é uma constante e tem uma derivada de tempo.

Implementada pelo método de modelagem estrutural, a matriz no ambiente SimInTech é semelhante à mostrada na Figura 1.

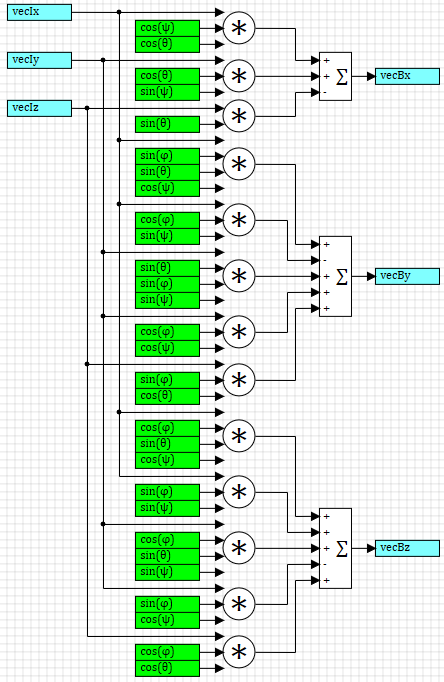
Figura 1. Matriz de rotação do sistema I para o sistema de coordenadas B

Então, para o vetor de velocidade linear, você pode escrever:

$$→vB(t)=REuB⋅→vEu(t),

e para o momento angular

$$→euB(t)=REuB⋅→euEu(t)...

Omitindo os cálculos intermediários (incluindo a derivada da matriz de rotação, que é basicamente igual ao produto vetorial da velocidade angular do objeto pela própria matriz de rotação, tomada com o sinal oposto), para a primeira das equações de dinâmica consideradas, obtemos a seguinte expressão no sistema de coordenadas B relacionado ao helicóptero :

$$d→vBdt=-→ωB(t)×→vB(t)+1m→FB(t),

e para a segunda equação, levando em consideração que $$→euB(t)=EuB⋅→ωB(t),

e uma vez que em um sistema de coordenadas limitadas rotativas, o tensor de inércia é uma constante e sua derivada de tempo é igual a zero, e$$d→euB(t)dt=EuB⋅d→ωB(t)dt Nós temos:

$$d→ωBdt=Eu-1B(→MB(t)-→ωB(t)×(EuB⋅→ωB(t)))...

No total, o registro II da lei de Newton para o referencial rotativo B, em comparação com as equações originais, foi suplementado com dois produtos vetoriais.

( 6 ) – . 6 – . 6 , SimInTech Simulink Scilab .

( B), I, , , , .

A única coisa que ainda não fizemos com as equações é que não escrevemos expressões para as forças e momentos que atuam no helicóptero. Vamos fazê-lo abaixo, na B sistema de coordenadas . De acordo com os pressupostos, levamos em consideração e denotamos por índices: M - o trabalho dos motores, apenas em termos da força de empuxo criada e momentos dela, D - a força da resistência do ar (junto com o vento), O - perturbação externa, geralmente zero, e definida arbitrariamente pelo usuário, a força da gravidade - não cria um momento de rotação de forças:

$$→FB(t)=→FM(t)+→FD(t)+→FO(t)+m⋅g⋅REuB⋅→eEuZ→MB(t)=→MM(t)+→MD(t)+→MO(t)

A gravidade no sistema de coordenadas vinculado "girará" com base na orientação da aeronave.

Vamos escrever com mais detalhes a que os termos são iguais:

$$→FM(t)=CT⋅ω2M1(t)⋅→eM1+CT⋅ω2M2(t)⋅→eM2+CT⋅ω2M3(t)⋅→eM3++CT⋅ω2M4(t)⋅→eM4+CT⋅ω2Mcinco(t)⋅→eMcinco+CT⋅ω2M6(t)⋅→eM6++CT⋅ω2M7(t)⋅→eM7+CT⋅ω2M8(t)⋅→eM8

As velocidades angulares de rotação do VMG, não do helicóptero, já são mencionadas aqui. Lembre-se de que os vetores unitários das forças de tração são escritos para o sistema de coordenadas B e existem constantes - é óbvio que eles podem ser calculados 1 vez, o coeficiente total é retirado do colchete aqui e os cálculos podem ser bastante simplificados. Se tivéssemos que escrever as equações da dinâmica no sistema I , essa expressão aumentaria mais 8 multiplicações pela matriz de rotação de cada ort, e isso teria que ser considerado em cada etapa do cálculo.

Força de resistência do ar (na ausência de vento):

$$→FD=-0,5ρ⋅CD⋅(UMAyz⋅vx⋅|vx|UMAxz⋅vy⋅|vy|UMAxy⋅vz⋅|vz|)

Perturbação externa - zero, a pedido do usuário, ele pode definir este ou aquele valor posteriormente, antes do cálculo, ou durante a simulação.

Escrevemos o momento das forças de empuxo dos motores como:

$$→MM(t)=→rM1×→eM1⋅CT⋅ω2M1(t)+→rM2×→eM2⋅CT⋅ω2M2(t)++→rM3×→eM3⋅CT⋅ω2M3(t)+→rM4×→eM4⋅CT⋅ω2M4(t)++→rMcinco×→eMcinco⋅CT⋅ω2Mcinco(t)+→rM6×→eM6⋅CT⋅ω2M6(t)+→rM7×→eM7⋅CT⋅ω2M7(t)+→rM8×→eM8⋅CT⋅ω2M8(t)

Momento de resistência do ar (para mais detalhes consulte [1]):

$$→MD=-0,5ρ⋅CD⋅(UMAyz⋅vx⋅|vx|⋅euxUMAxz⋅vy⋅|vy|⋅euy8UMAxy⋅vz⋅|vz|⋅euz)

Mais uma vez, notamos que o cálculo dos momentos de precessão e reativos do HMG é omitido neste artigo por brevidade.

Para evitar erros na transição de equações vetoriais para escalares, escritas nos eixos, é mais fácil aproveitar as vantagens do pacote MathCAD ou do tipo Maple, no qual a maioria das conversões pode ser realizada de forma automatizada, de forma simbólica, e obter as 6 equações necessárias da dinâmica registrada pelos eixos do sistema móvel de coordenadas Bed and .

Na forma mais compacta, as equações de dinâmica obtidas e resolvidas têm a seguinte aparência:

$$d→vBdt=1m(→FM(t)+→FD(t)+→FO(t))+gREuB→eEuz-→ωB(t)×→vB(t),d→ωBdt=Eu-1B(→MM(t)+→MD(t)-→ωB(t)×(EuB⋅→ωB(t))...

Ao integrá-los e obter os valores das velocidades no sistema B, pode-se calcular os ângulos de velocidade e orientação no sistema de coordenadas inerciais I:

$$→vEu(t)=RBEu⋅→vB(t),(˙φ˙θ˙ψ)=WBEu⋅→ωB(t)...

Sobre a matriz de transformação da velocidade angular do helicóptero para a taxa de giro pelos ângulos de Euler $$WBEu veja detalhes em [1].

3

– SimInTech. , , – . , , – . , , .

, – B 2 , ( ) 6 , 6 : . 6DOF , .. . , 6 , 6 ( ). . , ( ) – . , 12 . , , 18 . , 12 6 ( ) .

3.1

– , «», , . – 6- , . 2.

2 «» , 6+3+3 «». , ( ) – $$aBx,aBy,aBz,ωBx,ωBy,ωBz, – (, ).

I ( B ) , ,

, «» , ( ) I, B $$WBI. .

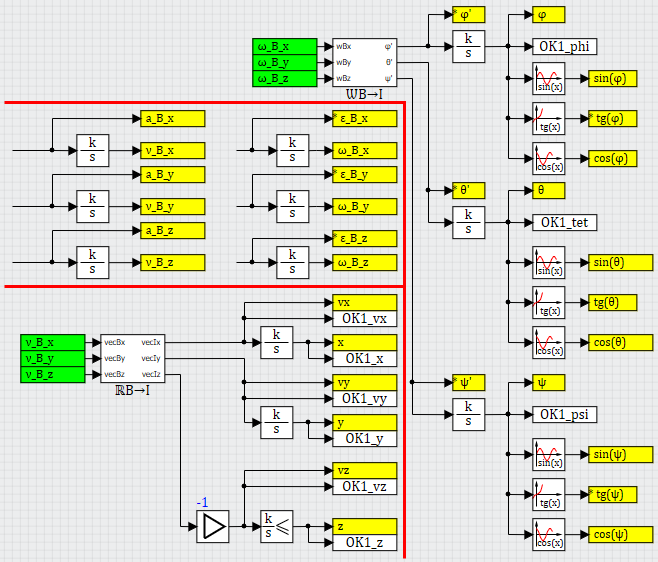
2.

« » « » – , 1 .

– ( a = F/m), x, 3:

3.

, .. - , – . , SimInTech ( , ).

W(B->I) B , . 4 [1] .

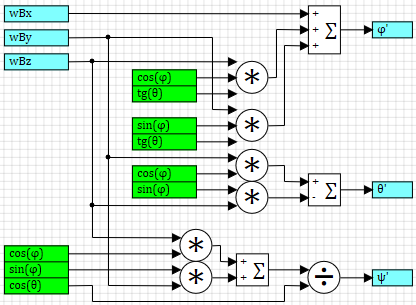
4. $$WBI

3.2

, 2 $$xB,yB,zBe desenhe o resultado no circuito SimInTech. Omitindo os cálculos (o leitor pode realizá-los de forma independente em uma folha de papel ou com a ajuda de algum software de matemática simbólica), apresentamos a forma final das equações. Devido ao inconveniente, citaremos os termos do lado direito.

Força de tração dos grupos de hélice $$→FM(t):

$$FMx(t)=1√2(-FM2(t)-FM4(t)+FM6(t)+FM8(t))⋅sEun(γ)++(FM3(t)-FM7(t))⋅sEun(γ),FMem(t)=1√2(FM2(t)-FM4(t)-FM6(t)+FM8(t))⋅sEun(γ)++(FMcinco(t)-FM1(t))⋅sEun(γ),FMz(t)=(FM1(t)+FM2(t)+FM3(t)+FM4(t)++FMcinco(t)+FM6(t)+FM8(t)+FM8(t))⋅cos(γ),

Onde $$FMEu(t) É a força de impulso do i-ésimo VMG no momento atual.

Força de resistência do ar $$→FD(t) na ausência de vento - as fórmulas são dadas acima, as projeções serão iguais:

$$FDx(t)=0,5⋅ρ⋅CD⋅UMAyz⋅vx⋅|vx|,FDem(t)=0,5⋅ρ⋅CD⋅UMAxz⋅vem⋅|vem|,FDz(t)=0,5⋅ρ⋅CD⋅UMAxy⋅vz⋅|vz|...

A força da gravidade, na projeção no eixo do sistema de coordenadas em movimento, o termo $$g⋅REuB⋅→eEuz será obviamente igual:

$$g⋅REuB⋅→eEuz=(-sEun(θ)sEun(ϕ)⋅cos(θ)cos(ϕ)⋅cos(θ))

E o último termo na equação para a velocidade linear do helicóptero é o produto vetorial das velocidades:

$$-→ωB(t)×→vB(t)=(vBz⋅ωBy-vBy⋅ωBzvBx⋅ωBz-vBz⋅ωBxvBy⋅ωBx-vBx⋅ωBy)...

Se substituirmos cuidadosamente as projeções obtidas na equação pela derivada da velocidade linear do helicóptero e, em seguida, implementarmos tudo isso no SimInTech, ao longo dos eixos, obteremos os seguintes diagramas estruturais apresentados nas Figuras 5, 6 e 7 (apenas as projeções são mostradas no eixo $$xB, nos outros eixos o resultado é semelhante até os termos):

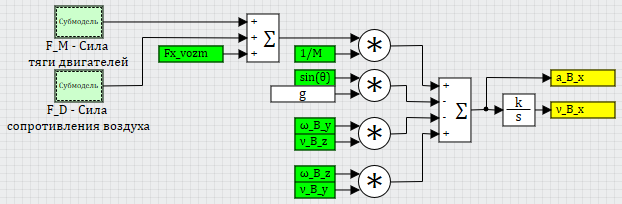
Figura 5. Aceleração linear do helicóptero ao longo do eixo $$xB...

Figura 6. A força de impulso do VMG ao longo do eixo $$xB...

Figura 7. Força de resistência do ar ao longo do eixo $$xB...

Portanto, nesta fase, implementamos totalmente uma das seis equações básicas (de acordo com a Figura 2 - calculamos a entrada para o primeiro integrador). O resto das entradas para as forças cortadas lá são calculadas de forma semelhante. Considere a equação para os momentos e para o cálculo da velocidade angular, ou melhor, seus termos do lado direito:

$$→Mm(t)+→MD(t)-→ωB(t)×(EuB⋅→ωB)

A soma dos momentos das forças de tração de todos os VMGs:

$$MMx(t)=[eu2√2(-FM2(t)-FM4(t)+FM6(t)+FM8(t))++eu1(FM7(t)-FM3(t))]⋅cos(γ),MMem(t)=[eu2√2(FM2(t)-FM4(t)-FM6(t)+FM8(t))++eu1(FM1(t)-FMcinco(t))]⋅cos(γ),MMz(t)=[eu2(FM2(t)+FM4(t)+FM6(t)+FM8(t))+-eu1(FM1(t)+FM3(t)+FMcinco(t)+FM7(t))]⋅sEun(γ)...

Onde $$FMEu(t) - força de tração do i-ésimo VMG no momento atual, $$eu1,eu2 - Forças de ombros (comprimentos das vigas do quadro do helicóptero para VMGs pares e ímpares).

Momento de resistência do ar (na ausência de vento):

$$MDx(t)=-0,5⋅ρ⋅CD⋅UMAyz⋅ωBx⋅|ωBx|⋅eux,MDem(t)=-0,5⋅ρ⋅CD⋅UMAxz⋅ωBy⋅|ωBy|⋅euy,MDz(t)=-0,5⋅ρ⋅CD⋅8⋅UMAxy⋅⋅ωBz⋅|ωBz|⋅euz...

O produto vetorial da velocidade angular e o produto do tensor de inércia e velocidade angular:

$$-→ωB(t)×(EuB⋅→ωB(t))=((Euyy-Euzz)⋅ωBy⋅ωBz(Euzz-Euxx)⋅ωBx⋅ωBz(Euxx-Euyy)⋅ωBx⋅ωBy)...

Assim, após substituir esses termos na equação diferencial para a velocidade angular, e implementar aquele obtido no ambiente SimInTech, obtemos os seguintes diagramas estruturais:

Figura 8. Aceleração angular do helicóptero em torno do eixo $$xB...

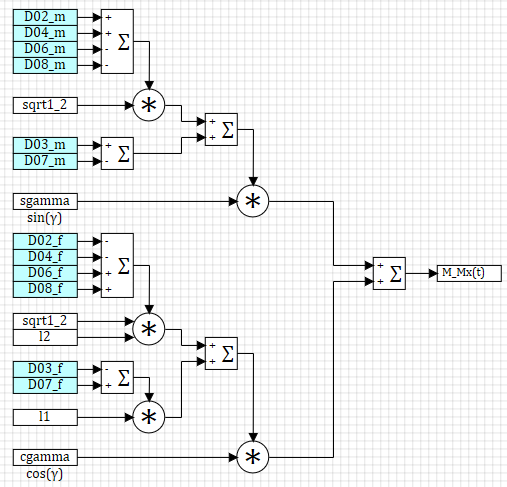
Figura 9. Momento das forças de empuxo de VMG em torno do eixo $$xB...

Figura 10. Força de resistência do ar ao girar $$xB...

3.3 Sistema de equações para a dinâmica do octocóptero na forma estrutural

, , ( 11). , , . (, , ), 6+ , , , . 12.

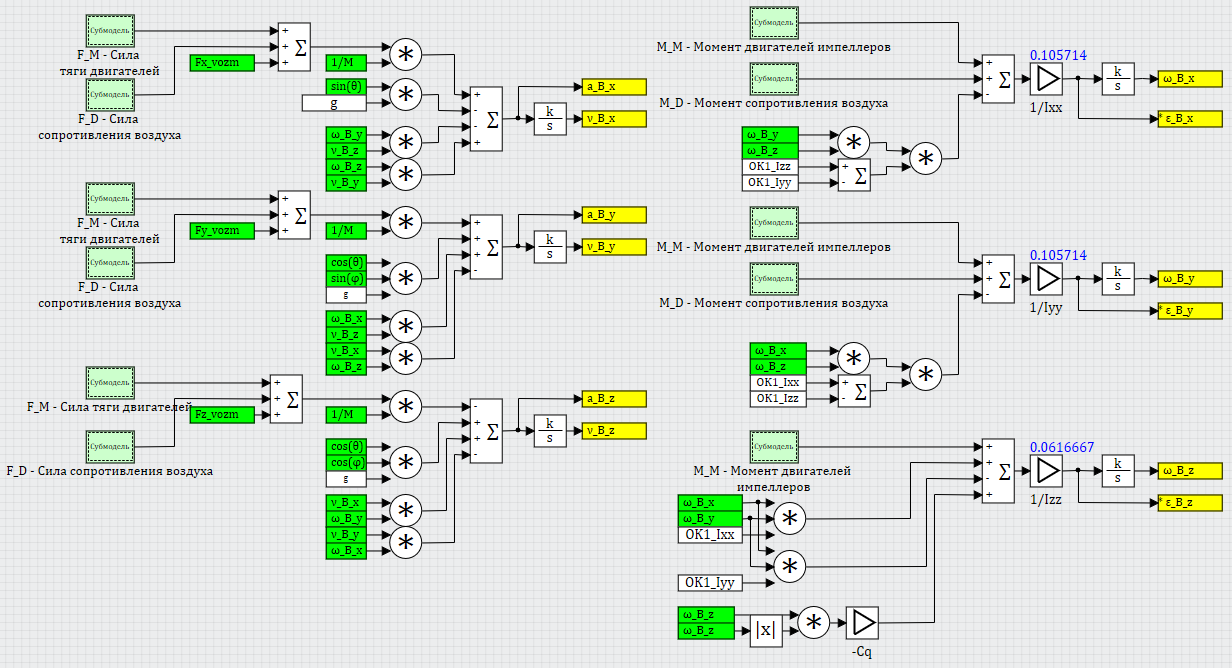
11. .

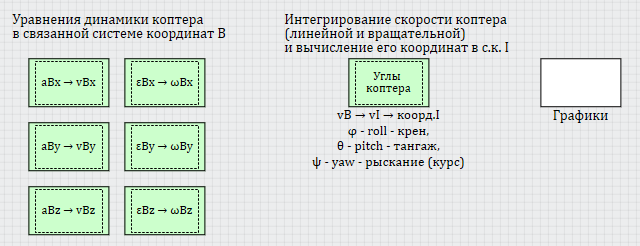
12. , .

, SimInTech, .

( , ), ( ) . , // - — , .

, () – B I, – I ( B .. – ).

, .

, , .

1. Design, Modeling and Control of an Octocopter, Oscar Oscarson, Royal Institute of Technology 2015
2. Development, Modelling and Control of a Multirotor Vehicle, Markus Mikkelsen, Umeå University 2015.