Olá, meu nome é David e aqui estou eu, renderizado por meu próprio desenho pintado à mão:





Infelizmente, não consegui encontrar um modelo gratuito de melhor qualidade , mas ainda assim expresso minha gratidão ao escultor estrangeiro que me capturou em digital! E como você deve ter adivinhado, falaremos sobre como escrever um processador de CPU.

Idéia

Com o desenvolvimento de linguagens de shader e o aumento do poder da GPU, mais e mais pessoas estão interessadas na programação gráfica. Novas direções surgiram, como Ray marchando com um rápido crescimento em sua popularidade.



Antecipando o lançamento de um novo monstro da NVidia, decidi escrever meu próprio artigo (tubo e old-school) sobre os fundamentos da renderização em uma CPU. É um reflexo da minha experiência pessoal de escrever um render e, nele, tentarei transmitir os conceitos e algoritmos que encontrei durante o processo de codificação. Deve ser entendido que o desempenho deste software será muito baixo devido à inadequação do processador para realizar tais tarefas.



A escolha da linguagem inicialmente caiu para c ++ ou ferrugem , mas me decidi por c #devido à facilidade de escrever o código e amplas oportunidades de otimização. O produto final deste artigo será um render capaz de produzir imagens como esta:







Todos os modelos que usei aqui são distribuídos em domínio público, não pirateie e respeite o trabalho dos artistas!

Matemáticas

Nem é preciso dizer onde escrever renderizações sem entender seus fundamentos matemáticos. Nesta seção, abordarei apenas os conceitos que usei no código. Não aconselho aqueles que não têm certeza de seus conhecimentos a pularem esta seção, sem entender esses fundamentos será difícil entender a próxima apresentação. Também espero que quem decidiu estudar geometria computacional tenha conhecimentos básicos em álgebra linear, geometria, bem como trigonometria (ângulos, vetores, matrizes, produto escalar). Para quem deseja compreender a geometria computacional mais profundamente, posso recomendar o livro de E. Nikulin "Computer Geometry and Computer Graphics Algorithms" .

Vector gira. Matriz de rotação

A rotação é uma das transformações lineares básicas do espaço vetorial. É também uma transformação ortogonal, pois preserva os comprimentos dos vetores transformados. Existem dois tipos de rotações no espaço 2D:

• Rotação em relação à origem
• Rotação sobre algum ponto

Aqui vou considerar apenas o primeiro tipo, uma vez que a segunda é uma derivada da primeira e difere apenas na mudança do sistema de coordenadas de rotação (analisaremos o sistema de coordenadas mais adiante).



Vamos derivar fórmulas para girar um vetor no espaço bidimensional. Vamos denotar as coordenadas do vetor original - {x, y} . As coordenadas do novo vetor, girado pelo ângulo f , serão denotadas como {x 'y'} .





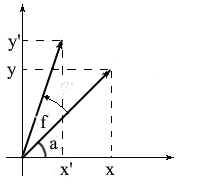
Sabemos que o comprimento desses vetores é comum e, portanto, podemos usar os conceitos de cosseno e seno para expressar esses vetores em termos de comprimento e ângulo em torno do eixo OX :





Observe que podemos usar as fórmulas de soma e cosseno para expandir os valores x ' e y' . Para aqueles que se esqueceram, vou lembrar estas fórmulas:





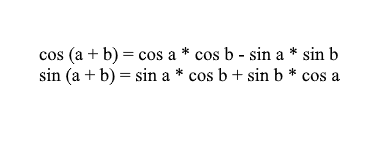
Expandindo as coordenadas do vetor girado através deles, obtemos:





É fácil ver aqui que os fatores l * cos a e l * sin a são as coordenadas do vetor original: x = l * cos a, y = l * sin a . Vamos substituí-los por x e y :





Assim, expressamos o vetor girado em termos das coordenadas do vetor original e do ângulo de sua rotação. Como uma matriz, esta expressão terá a seguinte aparência:





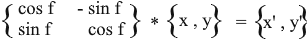
Multiplique e verifique se o resultado é equivalente ao que deduzimos.

Gire no espaço 3D

Consideramos a rotação no espaço bidimensional e também derivamos uma matriz para ela. Agora surge a pergunta: como obter essas transformações para três dimensões? No caso bidimensional, giramos vetores em um plano, mas aqui há um número infinito de planos em relação aos quais podemos fazer isso. No entanto, existem três tipos básicos de rotação com os quais você pode expressar qualquer rotação de um vetor no espaço tridimensional - rotações XY , XZ e YZ . Rotação



XY .



Com esta rotação, giramos o vetor em torno do eixo OZ do sistema de coordenadas. Imagine que os vetores são as hélices do helicóptero e o eixo OZ é o mastro em que se seguram. Com XYa rotação do vetor girará em torno do eixo OZ , como as pás de um helicóptero em relação ao mastro.





Note-se que com esta rotação, os z coordenadas dos vetores não mudam, mas o x e x coordenadas mudança - é por isso que este é chamado o XY rotação.





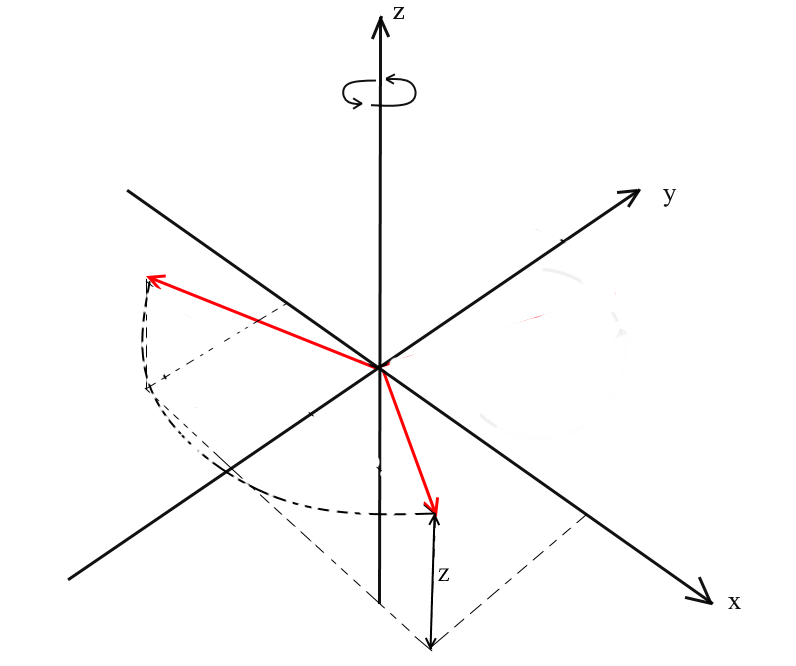
Não é difícil para as fórmulas da deriva para tal uma rotação: z - as coordenadas permanece o mesmo, e x e y mudança de acordo com os mesmos princípios que na rotação 2D.





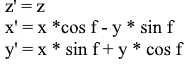
O mesmo na forma de uma matriz:





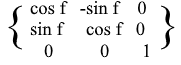
Para as rotações XZ e YZ , tudo é o mesmo:

Projeção

O conceito de projeção pode variar dependendo do contexto em que é usado. Muitos provavelmente já ouviram falar de conceitos como projeção em um plano ou projeção em um eixo de coordenadas.



No entendimento que usamos aqui, a projeção em um vetor também é um vetor. Suas coordenadas são o ponto de intersecção da perpendicular que caiu do vetor a para b com o vetor b .





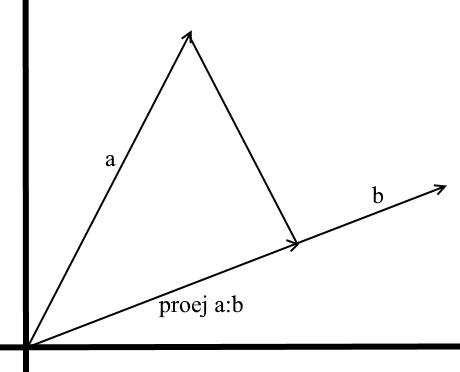
Para definir esse vetor, precisamos saber seu comprimento e direção . Como sabemos, a perna adjacente e a hipotenusa em um triângulo retângulo estão relacionadas pela razão de cosseno, então a usamos para expressar o comprimento do vetor de projeção:





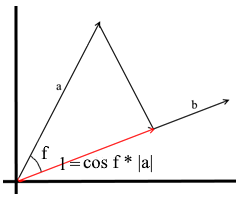
A direção do vetor de projeção por definição coincide com o vetor b , o que significa que a projeção é determinada pela fórmula:





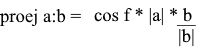
Aqui, obtemos a direção da projeção como um vetor unitário e a multiplicamos pelo comprimento da projeção. Não é difícil entender que o resultado será exatamente o que procuramos.



Agora vamos representar tudo em termos de produto escalar :





Obtemos uma fórmula conveniente para encontrar a projeção:

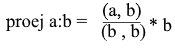
Sistemas coordenados. Bases

Muitos estão acostumados a trabalhar no sistema de coordenadas XYZ padrão , em que quaisquer 2 eixos serão perpendiculares entre si, e os eixos de coordenadas podem ser representados como vetores unitários:





Na verdade, existem infinitos sistemas de coordenadas, cada um deles é uma base . A base do espaço n- dimensional é um conjunto de vetores {v1, v2 …… vn} através dos quais todos os vetores deste espaço são representados. Nesse caso, nenhum vetor da base pode ser representado por seus outros vetores. Na verdade, cada base é um sistema de coordenadas separado, no qual os vetores terão suas próprias coordenadas exclusivas.



Vamos dar uma olhada no que é uma base para o espaço bidimensional. Tome, por exemplo, o conhecido sistema de coordenadas cartesianas de vetores X {1, 0} , Y {0, 1} , que é uma das bases para um espaço bidimensional:







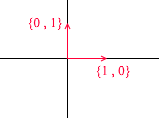
Qualquer vetor em um plano pode ser representado como uma soma de vetores dessa base com certos coeficientes ou como uma combinação linear . Lembre-se do que você faz quando escreve as coordenadas de um vetor - você escreve x - a coordenada e então - y . É assim que você realmente determina os coeficientes de expansão em termos dos vetores de base.







Agora vamos dar outra base:







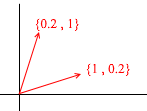
Qualquer vetor 2D também pode ser representado por meio de seus vetores:







Mas esse conjunto de vetores não é a base de um espaço bidimensional:







Nele, dois vetores {1,1} e {2,2} estão em uma linha reta. Quaisquer que sejam as combinações que você tomar, você receberá apenas vetores situados na linha reta comum y = x . Para nossos propósitos, esses defeituosos não serão úteis, no entanto, acho que vale a pena entender a diferença. Por definição, todas as bases são unidas por uma propriedade - nenhum dos vetores de base pode ser representado como uma soma de outros vetores de base com coeficientes, ou nenhum dos vetores de base é uma combinação linear de outros. Aqui está um exemplo de um conjunto de 3 vetores que também não é uma base :







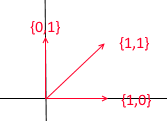
Qualquer vetor de um plano bidimensional pode ser expresso através dele , mas o vetor {1, 1} nele é supérfluo, pois ele mesmo pode ser expresso através dos vetores {1, 0} e {0,1} como {1,0} + {0,1 } .



Em geral, qualquer base de um espaço n- dimensional conterá exatamente n vetores, para 2e esse n é correspondentemente igual a 2.



Voltemos para 3d. A base tridimensional conterá 3 vetores:







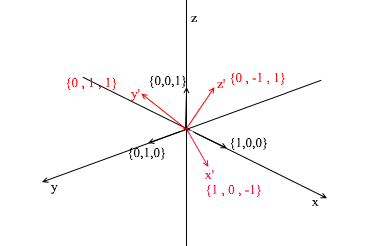
Se para uma base bidimensional bastasse dois vetores não estarem em uma linha reta, então em um espaço tridimensional um conjunto de vetores será uma base se:

• 1) 2 vetores não se encontram em uma linha reta
• 2) o terceiro não se situa no plano formado pelos outros dois.

A partir de agora, as bases com as quais trabalhamos serão ortogonais (qualquer um de seus vetores é perpendicular) e normalizadas (o comprimento de qualquer vetor de base é 1). Simplesmente não precisaremos de outros. Por exemplo, a base padrão







atende a esses critérios.

Transição para outra base

Até agora, escrevemos a decomposição de um vetor como uma soma de vetores de base com coeficientes:





Considere novamente a base padrão - o vetor {1, 3, 6} nele pode ser escrito da seguinte forma:





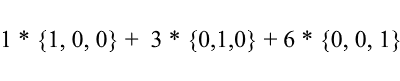
Como você pode ver, os coeficientes de expansão de um vetor na base são suas coordenadas nesta base . Vejamos o seguinte exemplo:







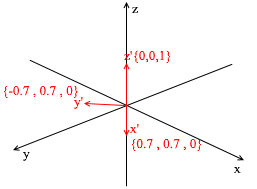
Esta base é derivada do padrão pela aplicação de uma rotação XY de 45 graus a ele . Pegue um vetor a no sistema padrão com coordenadas {0, 1, 1}







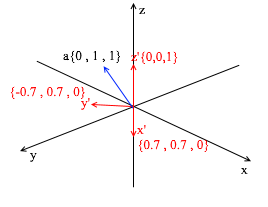
Por meio dos vetores da nova base, ela pode ser ampliada da seguinte forma:







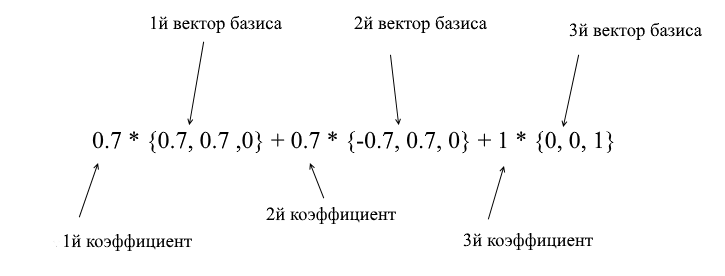
Se você calcular esse valor, obterá {0, 1, 1} - o vetor a na base padrão. Com base nessa expressão na nova base, o vetor a tem coordenadas {0,7, 0,7, 1} - os coeficientes de expansão. Isso ficará mais visível se você olhar de um ângulo diferente:







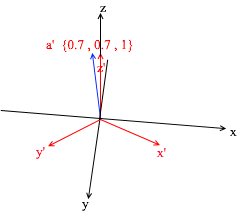
Mas como você encontra esses coeficientes? Em geral, um método universal é a solução de um sistema bastante complexo de equações lineares. No entanto, como eu disse antes, usaremos apenas as bases ortogonais e normalizadas , e para elas existe uma forma muito trapaceira. Consiste em encontrar projeções sobre os vetores de base. Vamos usá-lo para encontrar a decomposição do vetor a na base X {0,7, 0,7, 0} Y {-0,7, 0,7, 0} Z {0, 0, 1}







Primeiro, vamos encontrar o coeficiente para y ' . A primeira etapa é encontrar a projeção do vetor a no vetor y ' (discuti como fazer isso acima):







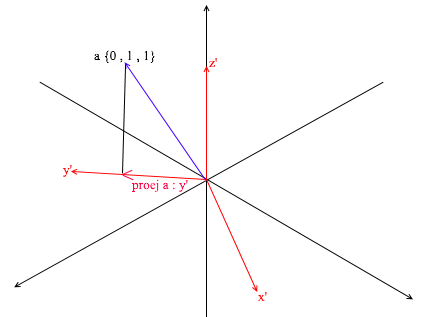
O segundo passo: dividimos o comprimento da projeção encontrada pelo comprimento do vetor y ' , assim, descobrimos “quantos vetores y' cabem no vetor de projeção” - este número será o coeficiente para y ' , e também y - a coordenada do vetor a na nova base! Para x ' e z', repita operações semelhantes:







Agora temos fórmulas para a transição de uma base padrão para uma nova:







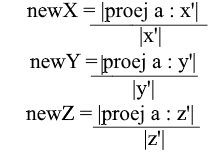
Bem, uma vez que usamos apenas bases normalizadas e os comprimentos de seus vetores são iguais a 1, não há necessidade de dividir pelo comprimento do vetor na fórmula de transição:







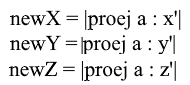
Expanda a coordenada x por meio da fórmula de projeção:







Observe que o denominador (x ', x') e o vetor x ' no caso de uma base normalizada também são iguais a 1 e podem ser descartados. Nós temos:







Vemos que a coordenada x na base é expressa como o produto escalar (a, x ') , a coordenada y, respectivamente, como (a, y') , a coordenada z é (a, z ') . Agora você pode criar uma matriz de transição para novas coordenadas:

Sistemas de coordenadas de deslocamento

Todos os sistemas de coordenadas que consideramos acima tiveram a origem do ponto {0,0,0} . Além disso, também existem sistemas com um ponto de origem deslocado:







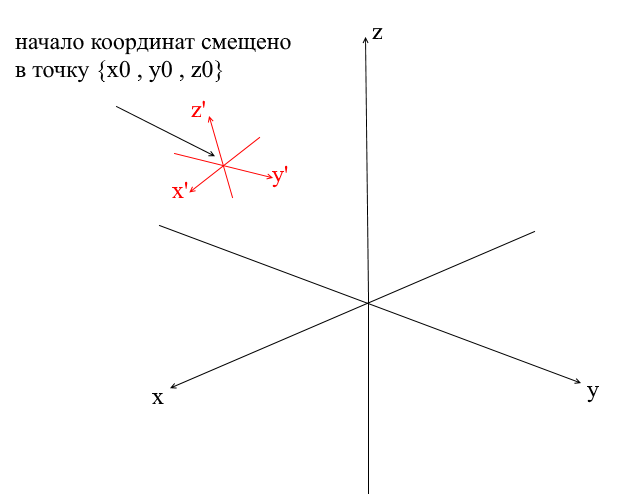
Para traduzir um vetor em tal sistema, você deve primeiro expressá-lo em relação ao novo centro de coordenadas. Para fazer isso é simples - subtraia este centro do vetor. Assim, você meio que "move" o próprio sistema de coordenadas para um novo centro, enquanto o vetor permanece no lugar. A seguir, você pode usar a matriz de transição que já conhecemos.

Escrevendo um mecanismo de geometria. Crie uma renderização de arame.

Bem, eu acho que alguém que passou pela seção com matemática e não fechou o artigo pode sofrer uma lavagem cerebral com coisas mais interessantes! Nesta seção, começaremos a escrever os fundamentos de um mecanismo 3D e renderização. Em geral, a renderização é um procedimento bastante complicado, que inclui muitas operações diferentes: cortar bordas invisíveis, rasterizar, calcular a luz, processar vários efeitos, materiais (às vezes até física). Analisaremos parcialmente tudo isso no futuro, mas agora faremos coisas mais simples - escreveremos uma renderização com fio . Sua essência é que ele desenha um objeto na forma de linhas conectando seus vértices, então o resultado parece uma rede de fios:

Gráficos poligonais

Tradicionalmente, os gráficos de computador usam representações poligonais de dados de objetos 3D. Assim, os dados são apresentados em OBJ, 3DS, FBX e muitos outros. Em um computador, esses dados são armazenados na forma de dois conjuntos: um conjunto de vértices e um conjunto de faces (polígonos). Cada vértice de um objeto é representado por sua posição no espaço - um vetor, e cada face (polígono) é representada por três inteiros que são índices dos vértices desse objeto. Os objetos mais simples (cubos, esferas, etc.) consistem em tais polígonos e são chamados de primitivos.



Em nosso motor, o primitivo será o objeto principal da geometria 3D - todos os outros objetos herdarão dele. Vamos descrever a classe do primitivo:

    abstract class Primitive
    {
        public Vector3[] Vertices { get; protected set; }
        public int[] Indexes { get; protected set; }
    }

Até agora, tudo é simples - existem vértices do primitivo e existem índices para formar polígonos. Agora você pode usar esta classe para criar um cubo:

   public class Cube : Primitive
      {
        public Cube(Vector3 center, float sideLen)
        {
            var d = sideLen / 2;
            Vertices = new Vector3[]
                {
                    new Vector3(center.X - d , center.Y - d, center.Z - d) ,
                    new Vector3(center.X - d , center.Y - d, center.Z) ,
                    new Vector3(center.X - d , center.Y , center.Z - d) ,
                    new Vector3(center.X - d , center.Y , center.Z) ,
                    new Vector3(center.X + d , center.Y - d, center.Z - d) ,
                    new Vector3(center.X + d , center.Y - d, center.Z) ,
                    new Vector3(center.X + d , center.Y + d, center.Z - d) ,
                    new Vector3(center.X + d , center.Y + d, center.Z + d) ,
                };

            Indexes = new int[]
                {
                    1,2,4 ,
                    1,3,4 ,
                    1,2,6 ,
                    1,5,6 ,
                    5,6,8 ,
                    5,7,8 ,
                    8,4,3 ,
                    8,7,3 ,
                    4,2,8 ,
                    2,8,6 ,
                    3,1,7 ,
                    1,7,5
                };
        }
    }

int Main()
{
        var cube = new Cube(new Vector3(0, 0, 0), 2);
}

Implementando sistemas de coordenadas

Não basta definir um objeto com um conjunto de polígonos, para planejar e criar cenas complexas, é preciso colocar os objetos em lugares diferentes, girá-los, reduzi-los ou aumentá-los de tamanho. Para a conveniência dessas operações, os chamados sistemas de coordenadas locais e globais são usados. Cada objeto na cena possui seu próprio sistema de coordenadas - local, bem como seu próprio ponto central.





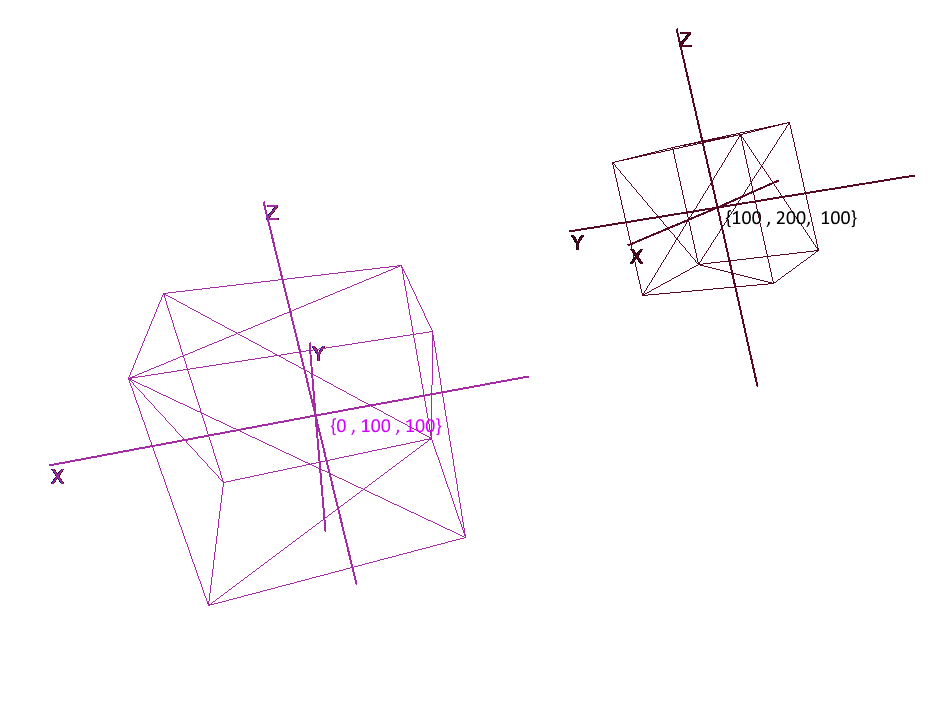
A representação de um objeto em coordenadas locais permite que você execute facilmente qualquer operação com ele. Por exemplo, para mover um objeto pelo vetor a , será suficiente deslocar o centro de seu sistema de coordenadas por este vetor, para girar um objeto - girar suas coordenadas locais.



Ao trabalhar com um objeto, vamos realizar operações com seus vértices no sistema de coordenadas local; durante a renderização, vamos primeiro traduzir todos os objetos na cena em um único sistema de coordenadas - o global. Vamos adicionar sistemas de coordenadas ao código. Para fazer isso, crie um objeto da classe Pivot (pivô, ponto pivô) que representará a base local do objeto e seu ponto central. A conversão de um ponto em um sistema de coordenadas apresentado pelo Pivot será feita em 2 etapas:

• 1) Representação de um ponto em relação ao centro de novas coordenadas
• 2) Expansão em vetores da nova base

Pelo contrário, para representar o vértice local de um objeto em coordenadas globais, você deve executar estas ações na ordem inversa:

• 1) Expansão em vetores de base global
• 2) Representação em relação ao centro global

Vamos escrever uma classe para representar sistemas de coordenadas:

    public class Pivot
    {
        // 
        public Vector3 Center { get; private set; }
        //   -   
        public Vector3 XAxis { get; private set; }
        public Vector3 YAxis { get; private set; }
        public Vector3 ZAxis { get; private set; }

        //    
        public Matrix3x3 LocalCoordsMatrix => new Matrix3x3
            (
                XAxis.X, YAxis.X, ZAxis.X,
                XAxis.Y, YAxis.Y, ZAxis.Y,
                XAxis.Z, YAxis.Z, ZAxis.Z
            );

        //    
        public Matrix3x3 GlobalCoordsMatrix => new Matrix3x3
            (
                XAxis.X , XAxis.Y , XAxis.Z,
                YAxis.X , YAxis.Y , YAxis.Z,
                ZAxis.X , ZAxis.Y , ZAxis.Z
            );

        public Vector3 ToLocalCoords(Vector3 global)
        {
            //          
            return LocalCoordsMatrix * (global - Center);
        }
        public Vector3 ToGlobalCoords(Vector3 local)
        {
            //    -            
            return (GlobalCoordsMatrix * local)  + Center;
        }

        public void Move(Vector3 v)
        {
            Center += v;
        }

        public void Rotate(float angle, Axis axis)
        {
            XAxis = XAxis.Rotate(angle, axis);
            YAxis = YAxis.Rotate(angle, axis);
            ZAxis = ZAxis.Rotate(angle, axis);
        }
    }

Agora, usando esta classe, adicione as funções de rotação, movimento e aumento às primitivas:

    public abstract class Primitive
    {
        //  
        public Pivot Pivot { get; protected set; }
        // 
        public Vector3[] LocalVertices { get; protected set; }
        // 
        public Vector3[] GlobalVertices { get; protected set; }
        // 
        public int[] Indexes { get; protected set; }

        public void Move(Vector3 v)
        {
            Pivot.Move(v);

            for (int i = 0; i < LocalVertices.Length; i++)
                GlobalVertices[i] += v;
        }

        public void Rotate(float angle, Axis axis)
        {
            Pivot.Rotate(angle , axis);

            for (int i = 0; i < LocalVertices.Length; i++)
                GlobalVertices[i] = Pivot.ToGlobalCoords(LocalVertices[i]);
        }

        public void Scale(float k)
        {
            for (int i = 0; i < LocalVertices.Length; i++)
                LocalVertices[i] *= k;

            for (int i = 0; i < LocalVertices.Length; i++)
                GlobalVertices[i] = Pivot.ToGlobalCoords(LocalVertices[i]);
        }
    }

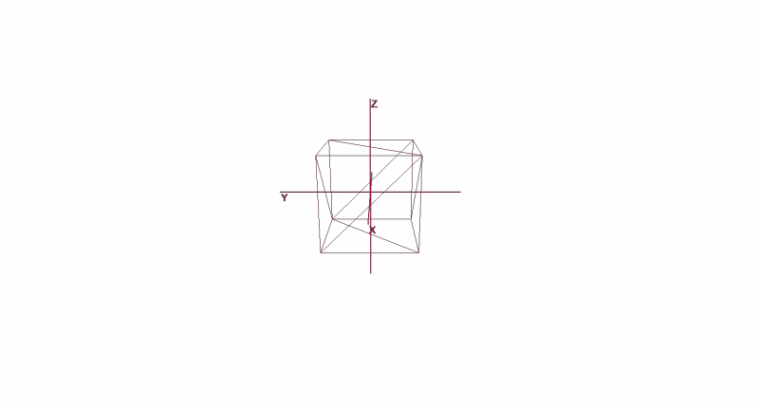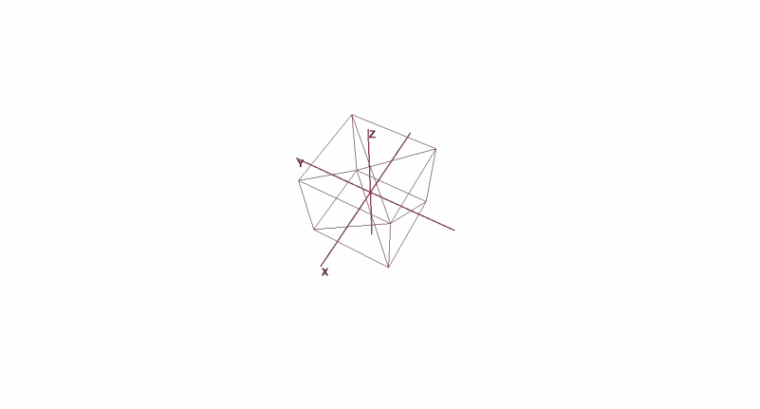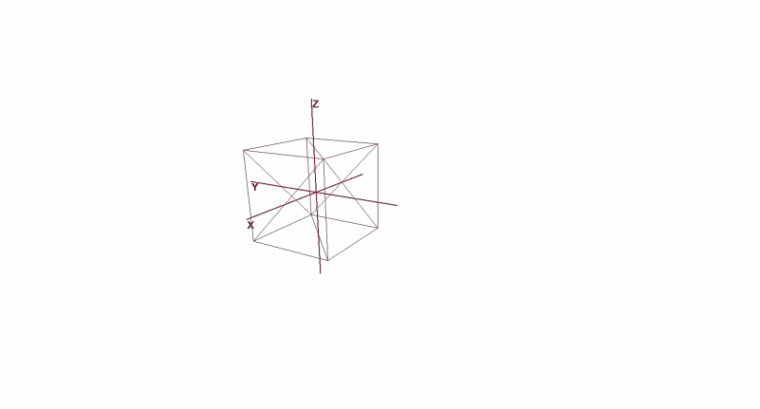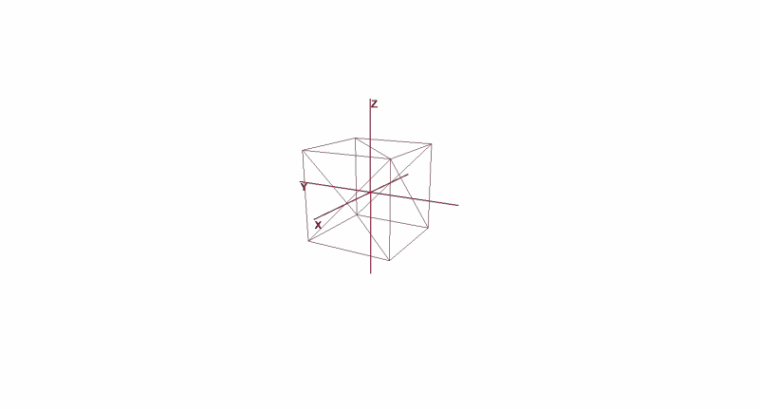
Girando e movendo um objeto usando coordenadas locais

Desenhando polígonos. Câmera

O objeto principal da cena será a câmera - com a ajuda dela, objetos serão desenhados na tela. A câmera, como todos os objetos na cena, terá coordenadas locais na forma de um objeto da classe Pivot - através dela moveremos e giraremos a câmera:





Para exibir o objeto na tela, usaremos um método simples de projeção em perspectiva . O princípio no qual este método se baseia é que quanto mais longe de nós o objeto está, menor ele parecerá. Provavelmente muitas pessoas já resolveram o problema na escola sobre medir a altura de uma árvore localizada a uma certa distância do observador:





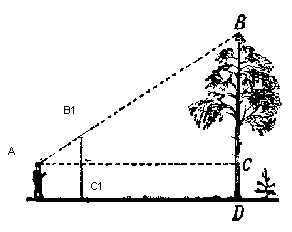
Imagine que um raio do ponto superior de uma árvore cai em um certo plano de projeção localizado a uma distância C1 do observador e desenha um ponto nele. O observador vê este ponto e deseja determinar a altura da árvore a partir dele. Como você pode ver, a altura da árvore e a altura de um ponto no plano de projeção estão relacionadas pela proporção de triângulos semelhantes. Então o observador pode determinar a altura do ponto usando esta proporção:







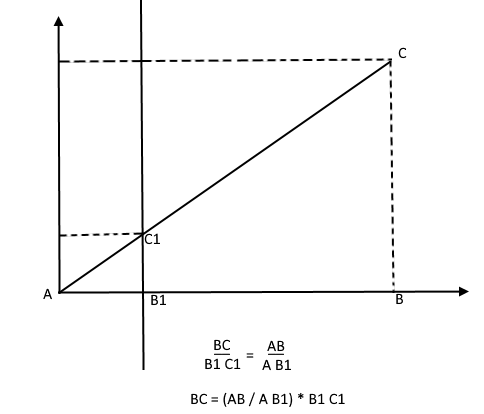
Ao contrário, sabendo a altura da árvore, ele pode encontrar a altura de um ponto no plano de projeção:







Agora vamos voltar para nossa câmera. Imagine que um plano de projeção está ligado ao eixo z das coordenadas da câmera a uma distância z ' da origem. A fórmula para tal plano é z = z ' , ela pode ser dada por um número - z' . Os raios dos vértices de vários objetos caem neste plano. Quando o raio atinge o plano, ele deixa um ponto nele. Ao conectar esses pontos, você pode desenhar um objeto.







Este plano representará a tela. Encontraremos a coordenada da projeção do vértice do objeto na tela em 2 etapas:

• 1) Nós traduzimos o vértice nas coordenadas locais da câmera
• 2) Encontre a projeção de um ponto através da proporção de triângulos semelhantes

A projeção será um vetor bidimensional, suas coordenadas x 'ey' definirão a posição do ponto na tela do computador.





Este código contém vários erros, que falaremos sobre consertar mais tarde.

Corte polígonos invisíveis

Tendo projetado três pontos do polígono na tela desta forma, obtemos as coordenadas do triângulo que correspondem à exibição do polígono na tela. Mas desta forma a câmera irá processar quaisquer vértices, incluindo aqueles cujas projeções vão além da área da tela, se você tentar desenhar tal vértice, há uma grande probabilidade de detectar erros. A câmera também processará os polígonos que estão atrás dela (as coordenadas z de seus pontos na linha de base da câmera local são menores que z ' ) - também não precisamos dessa visão "occipital".







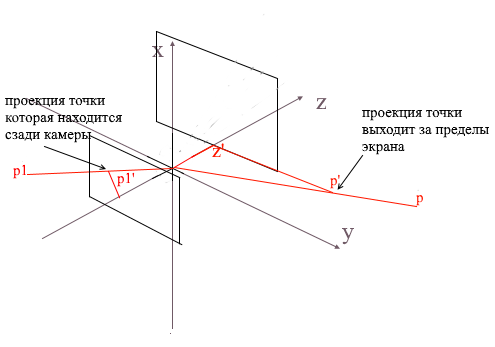
Para recortar vértices invisíveis em gl aberto, o método da pirâmide de truncamento é usado. Consiste em definir dois planos - próximo (plano próximo) e distante (plano distante). Tudo o que se encontra entre esses dois planos estará sujeito a processamento posterior. Eu uso uma versão simplificada com um plano de recorte - z ' . Todos os vértices atrás dele ficarão invisíveis.



Vamos adicionar dois novos campos à câmera - largura e altura da tela.

Agora vamos verificar cada ponto projetado para atingir a área da tela. Também vamos cortar os pontos atrás da câmera. Se o ponto estiver atrás ou sua projeção não cair na tela, o método retornará o ponto {float.NaN, float.NaN} .

Traduzir para as coordenadas da tela

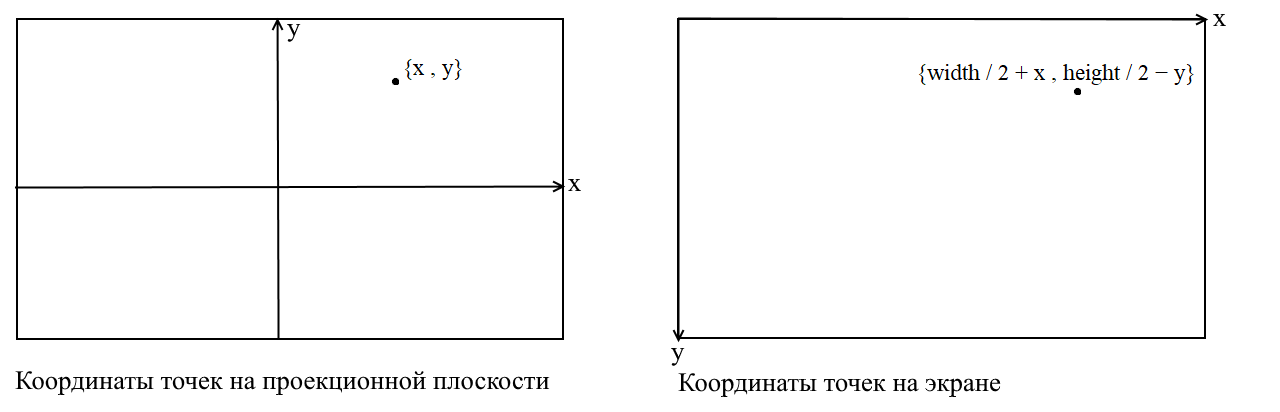
Aqui vou esclarecer um ponto. Está relacionado ao fato de que em muitas bibliotecas gráficas o desenho ocorre no sistema de coordenadas da tela, em tais coordenadas a origem é o ponto superior esquerdo da tela, x aumenta quando se move para a direita ey quando se move para baixo. Em nosso plano de projeção, os pontos são representados em coordenadas cartesianas comuns e, antes de desenhar, essas coordenadas devem ser convertidas em coordenadas de tela. Isso é fácil de fazer, você só precisa deslocar a origem para o canto superior esquerdo e inverter y :

Ajustando o tamanho da imagem projetada

Se você usar o código anterior para desenhar um objeto, obterá algo assim:







Por alguma razão, todos os objetos são desenhados muito pequenos. A fim de compreender a razão, lembrar como nós calculada a projecção - multiplicou-se o x e y coordenadas pelo delta do Z '/ z proporção . Isso significa que o tamanho do objeto na tela depende da distância ao plano de projeção z ' . Mas podemos definir z ' tão pequeno quanto quisermos. Isso significa que precisamos ajustar o tamanho da projeção dependendo do valor z ' atual . Para fazer isso, vamos adicionar outro campo à câmera - seu ângulo de visão .







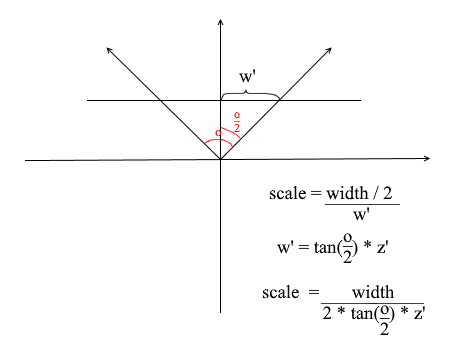
Precisamos que ele corresponda ao tamanho angular da tela com sua largura. O ângulo será combinado com a largura da tela desta forma: o ângulo máximo dentro do qual a câmera está olhando é a borda esquerda ou direita da tela. Então, o ângulo máximo do eixo z da câmera é o / 2 . A projeção que atinge a borda direita da tela deve ter a coordenada x = largura / 2 , e a esquerda: x = -largura / 2 . Sabendo disso, derivamos a fórmula para encontrar o coeficiente de alongamento da projeção:









Aqui está um código de renderização simples que usei para o teste:





Vamos verificar a renderização na cena e nos cubos:







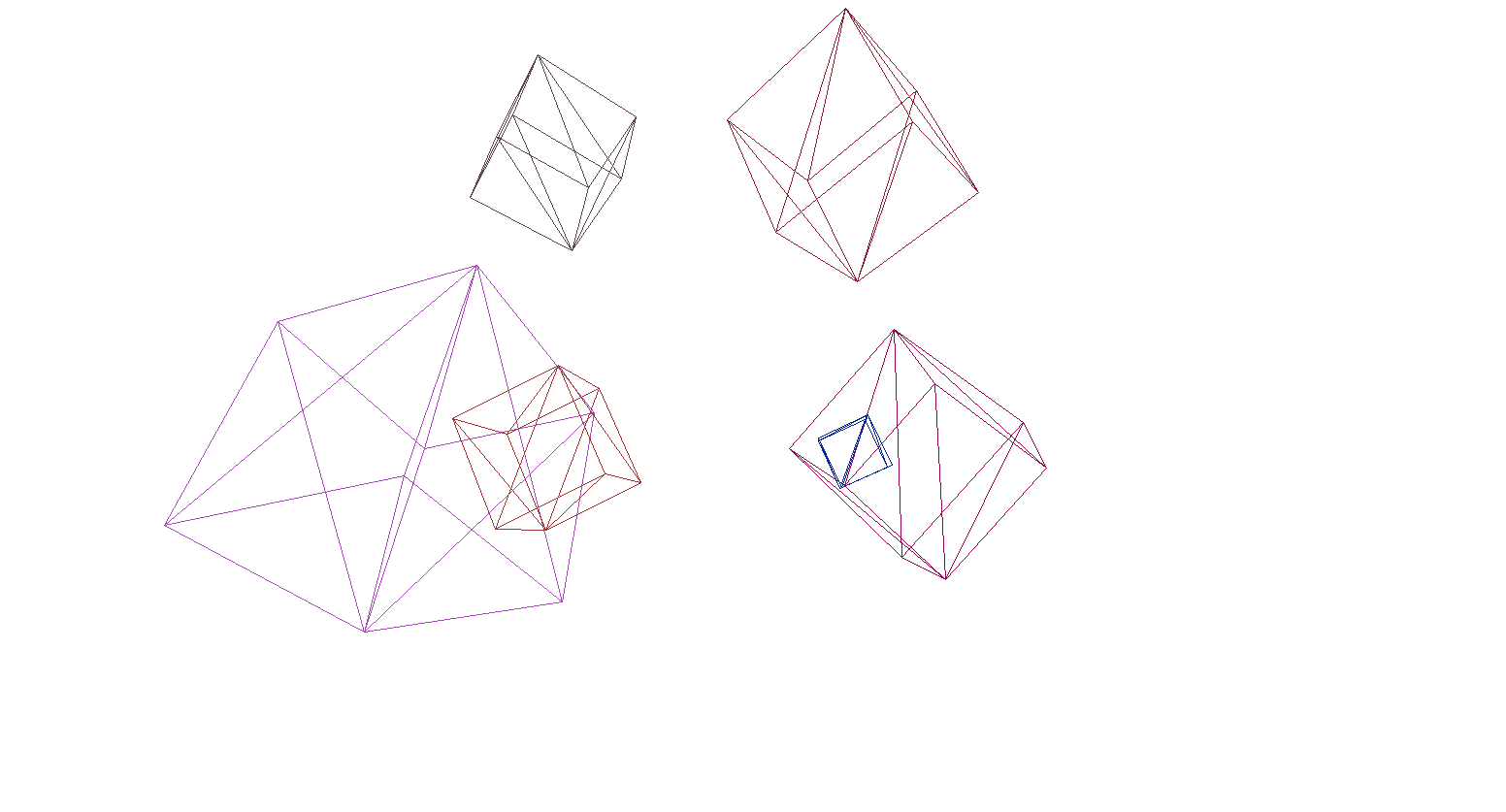
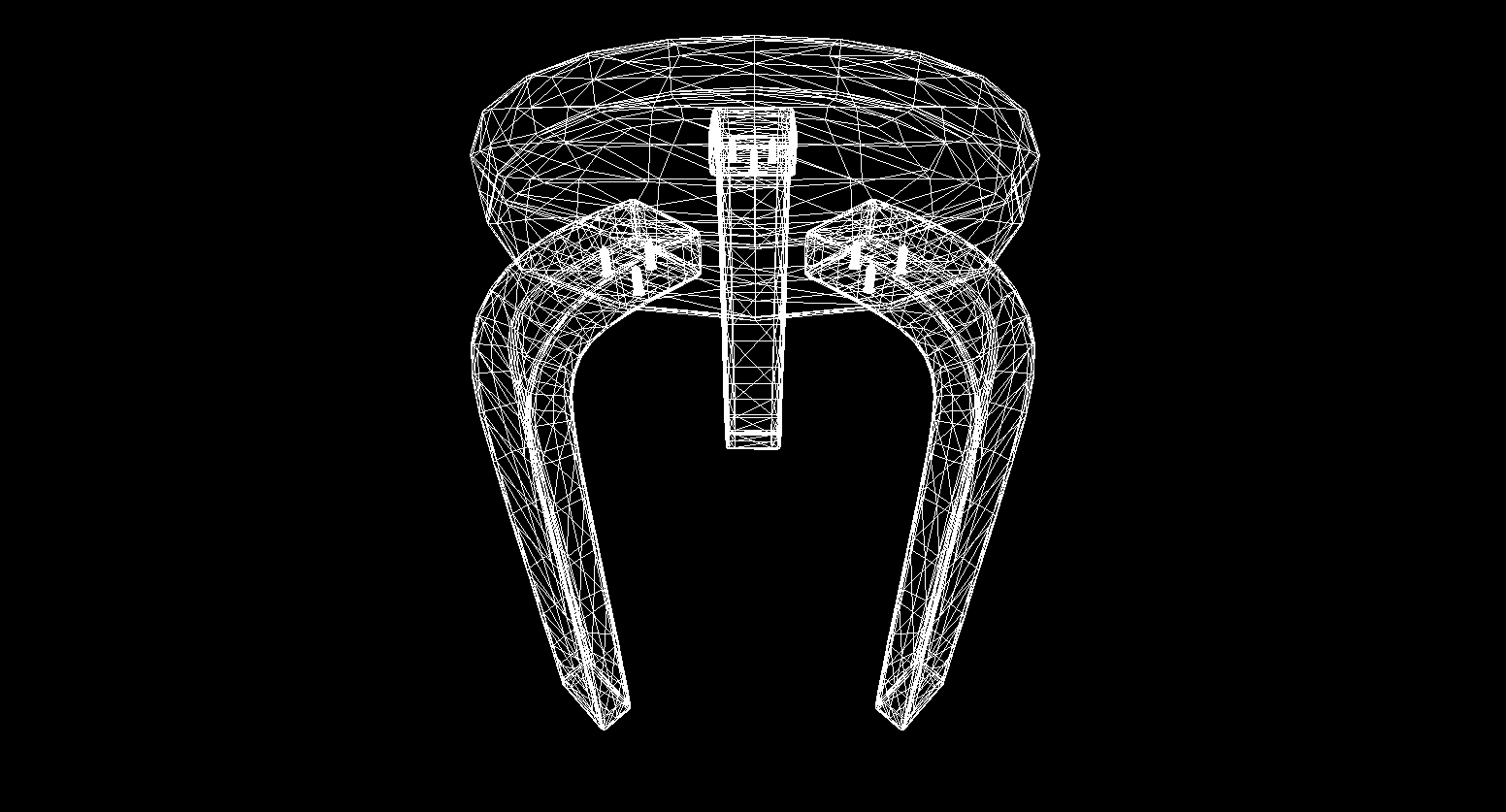
E sim, tudo funciona muito bem. Para quem não acha os cubos coloridos pretensiosos, escrevi uma função para analisar modelos de formato OBJ em objetos primitivos, preenchi o fundo com preto e renderizei vários modelos:

Rasterização de polígonos. Trazemos beleza.

Na última seção, escrevemos uma renderização de wireframe. Agora trataremos de sua modernização - implementaremos a rasterização de polígonos.



Simplesmente rasterizar um polígono significa pintar sobre ele. Pareceria por que escrever uma bicicleta quando já existem funções de rasterização de triângulos prontas. Veja o que acontece se você desenhar tudo com as ferramentas padrão:







Arte contemporânea, polígonos atrás dos frontais foram desenhados, em uma palavra - mingau. Além disso, como você texturiza objetos dessa maneira? Sim, de jeito nenhum. Portanto, precisamos escrever nosso próprio imba-rasterizador, que será capaz de cortar pontos invisíveis , texturas e até mesmo shaders! Mas, para fazer isso, vale a pena entender como pintar triângulos em geral.

Algoritmo de Bresenham para Desenho de Linha.

Vamos começar com as falas. Se alguém não conhecesse o algoritmo de Bresenham, este é o principal algoritmo para desenhar linhas retas em computação gráfica. Ele ou suas modificações são usadas literalmente em todos os lugares: desenhar linhas, segmentos, círculos, etc. Quem estiver interessado em uma descrição mais detalhada - leia o wiki. Algoritmo de Bresenham



Há um segmento de linha conectando os pontos {x1, y1} e {x2, y2} . Para desenhar um segmento entre eles, você precisa pintar sobre todos os pixels que caem sobre ele. Para dois pontos do segmento, você pode encontrar as coordenadas x dos pixels nos quais eles se encontram: você só precisa pegar partes inteiras das coordenadas x1 e x2 . Para pintar os pixels no segmento, iniciamos o ciclo de x1 a x2 e a cada iteração calculamosy - coordenada do pixel que cai na linha. Aqui está o código:

void Brezenkhem(Vector2 p1 , Vector2 p2)
{
    int x1 = Floor(p1.X);
    int x2 = Floor(p2.X);
    if (x1 > x2) {Swap(x1, x2); Swap(p1 , p2);}
    float d = (p2.Y - p1.Y) / (x2 - x1);
    float y = p1.Y;
    for (int i = x1; i <= x2; i++)
    {
        int pixelY = Floor(y);
        FillPixel(i , pixelY);
        y += d;
    }
}

Imagem da wiki

Rasterize um triângulo. Algoritmo de Preenchimento

Sabemos desenhar linhas, mas com triângulos vai ser um pouco mais difícil (não muito)! A tarefa de desenhar um triângulo é reduzida a várias tarefas de desenhar linhas. Primeiro, vamos dividir o triângulo em duas partes, tendo previamente classificado os pontos em ordem crescente x :







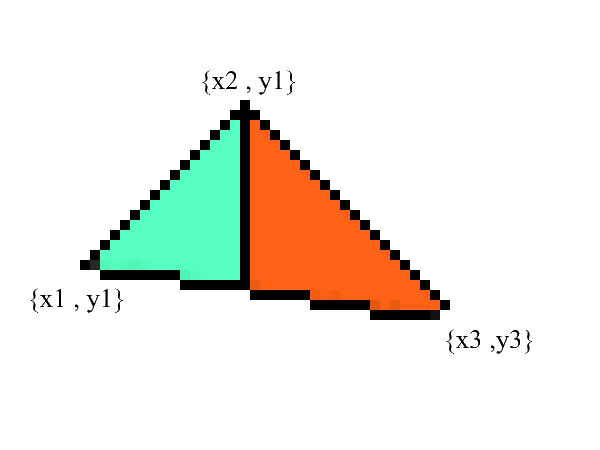
Observe - agora temos duas partes nas quais as bordas inferior e superior estão claramente expressas . tudo o que resta é preencher todos os pixels intermediários! Isso pode ser feito em 2 ciclos: de x1 a x2 e de x3 a x2 .

void Triangle(Vector2 v1 , Vector2 v2 , Vector2 v3)
{
    // BubbleSort    x
    if (v1.X > v2.X) { Swap(v1, v2); }
    if (v2.X > v3.X) { Swap(v2, v3); }
    if (v1.X > v2.X) { Swap(v1, v2); }

    //    y    x
    //   0:  x1 == x2     - 
    var steps12 = max(v2.X - v1.X , 1);
    var steps13 = max(v3.X - v1.X , 1);
    var upDelta = (v2.Y - v1.Y) / steps12;
    var downDelta = (v3.Y - v1.Y) / steps13;

    //     
    if (upDelta < downDelta) Swap(upDelta , downDelta);

    //     y1
    var up = v1.Y;
    var down = v1.Y;

    for (int i = (int)v1.X; i <= (int)v2.X; i++)
    {
        for (int g = (int)down; g <= (int)up; g++)
        {
            FillPixel(i , g);
        }
        up += upDelta;
        down += downDelta;
    }

    //       
    var steps32 = max(v2.X - v3.X , 1);
    var steps31 = max(v1.X - v3.X , 1);
    upDelta = (v2.Y - v3.Y) / steps32;
    downDelta = (v1.Y - v3.Y) / steps31;

    if (upDelta < downDelta) Swap(upDelta, downDelta);

    up = v3.Y;
    down = v3.Y;

    for (int i = (int)v3.X; i >=(int)v2.X; i--)
    {
        for (int g = (int)down; g <= (int)up; g++)
        {
            FillPixel(i, g);
        }
        up += upDelta;
        down += downDelta;
    }
}

Sem dúvida, esse código pode ser refatorado e não para duplicar o loop:

void Triangle(Vector2 v1 , Vector2 v2 , Vector2 v3)
{
    if (v1.X > v2.X) { Swap(v1, v2); }
    if (v2.X > v3.X) { Swap(v2, v3); }
    if (v1.X > v2.X) { Swap(v1, v2); }

    var steps12 = max(v2.X - v1.X , 1);
    var steps13 = max(v3.X - v1.X , 1);
    var steps32 = max(v2.X - v3.X , 1);
    var steps31 = max(v1.X - v3.X , 1);

    var upDelta = (v2.Y - v1.Y) / steps12;
    var downDelta = (v3.Y - v1.Y) / steps13;
    if (upDelta < downDelta) Swap(upDelta , downDelta);

    TrianglePart(v1.X , v2.X , v1.Y , upDelta , downDelta);

    upDelta = (v2.Y - v3.Y) / steps32;
    downDelta = (v1.Y - v3.Y) / steps31;
    if (upDelta < downDelta) Swap(upDelta, downDelta);

    TrianglePart(v3.X, v2.X, v3.Y, upDelta, downDelta);
}

void TrianglePart(float x1 , float x2 , float y1  , float upDelta , float downDelta)
{
    float up = y1, down = y1;
    for (int i = (int)x1; i <= (int)x2; i++)
    {
        for (int g = (int)down; g <= (int)up; g++)
        {
            FillPixel(i , g);
        }
        up += upDelta; down += downDelta;
    }
}

Recortando pontos invisíveis.

Primeiro, pense em como você vê. Agora, há uma tela à sua frente e o que está atrás dela está oculto aos seus olhos. Na renderização, um mecanismo semelhante funciona - se um polígono se sobrepõe a outro, a renderização o desenha sobre o sobreposto. Pelo contrário, não desenhará a parte fechada do polígono:







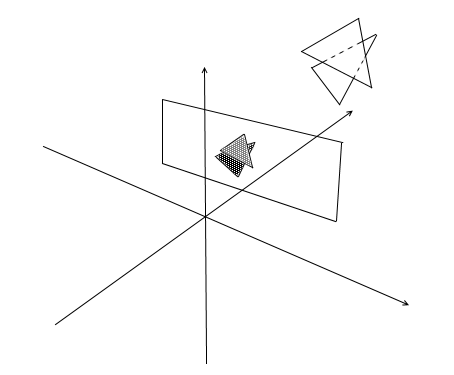
Para entender se os pontos são visíveis ou não, o mecanismo zbuffer (buffer de profundidade) é usado na renderização . zbuffer pode ser pensado como um array bidimensional (pode ser compactado em unidimensional) com largura * altura . Para cada pixel na tela, ele armazena um valor z - as coordenadas no polígono original de onde esse ponto foi projetado. Conseqüentemente, quanto mais próximo o ponto estiver do observador, menor será sua coordenada z . Em última análise, se as projeções de vários pontos coincidem, você precisa rasterizar o ponto com a coordenada z mínima :







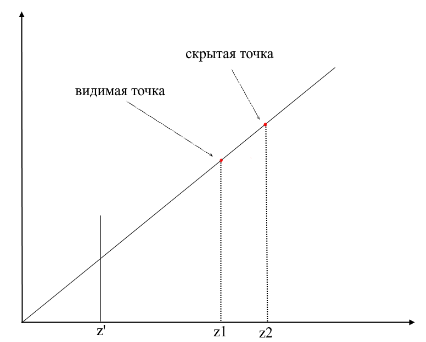
Agora surge a pergunta - como encontrar as coordenadas z dos pontos no polígono original? Isto pode ser feito de várias maneiras. Por exemplo, você pode atirar em um raio da origem da câmera, passando por um ponto no plano de projeção {x, y, z '} e encontrar sua intersecção com o polígono. Mas procurar cruzamentos é uma operação extremamente cara, portanto, usaremos um método diferente. Para desenhar um triângulo, interpolamos as coordenadas de suas projeções , agora, além disso, iremos interpolar também as coordenadas do polígono original . Para cortar pontos invisíveis, usaremos o estado zbuffer para o quadro atual no método de rasterização .



Meu zbuffer se parecerá comVector3 [] - ele conterá não apenas coordenadas z , mas também valores interpolados de pontos poligonais (fragmentos) para cada pixel da tela. Isso é feito para economizar memória, pois no futuro ainda precisaremos desses valores para escrever shaders ! Nesse ínterim, temos o seguinte código para determinar os vértices (fragmentos) visíveis :







Animação das etapas do rasterizador (ao reescrever a profundidade no zbuffer, o pixel é destacado em vermelho):



Por conveniência, movi todo o código para um módulo Rasterizador separado:





Agora vamos verificar o trabalho de renderização. Para isso utilizo o modelo de Sylvanas do famoso RPG "WOW":







Não é muito claro, certo? Isso ocorre porque não há texturas ou iluminação aqui. Mas vamos consertar isso em breve.

Texturas! Normal! Iluminação! Motor!

Por que eu combinei tudo em uma seção? E porque, em essência, a texturização e o cálculo de normais são absolutamente idênticos e você logo entenderá isso.



Primeiro, vamos examinar o problema de texturização de um polígono. Agora, além das coordenadas usuais dos vértices do polígono, também armazenaremos suas coordenadas de textura . A coordenada de textura do vértice é representada como um vetor 2D e aponta para um pixel na imagem de textura. Encontrei uma boa foto na internet para mostrar isso:





Observe que o início da textura ( pixel inferior esquerdo ) nas coordenadas de textura é {0, 0} e o final ( pixel superior direito ) é {1, 1} . Leve em consideração o sistema de coordenadas da textura e a possibilidade de ir além das bordas da imagem quando a coordenada da textura for 1.



Vamos criar uma classe para representar os dados do vértice imediatamente:

  public class Vertex
    {
        public Vector3 Position { get; set; }
        public Color Color { get; set; }
        public Vector2 TextureCoord { get; set; }
        public Vector3 Normal { get; set; }

        public Vertex(Vector3 pos , Color color , Vector2 texCoord , Vector3 normal)
        {
            Position = pos;
            Color = color;
            TextureCoord = texCoord;
            Normal = normal;
        }
    }

Explicarei porque os normais são necessários mais tarde, por enquanto saberemos apenas que os vértices podem tê-los. Agora, para texturizar o polígono, precisamos mapear de alguma forma o valor da cor da textura para um pixel específico. Lembra como interpolamos os vértices? Faça o mesmo aqui! Não vou reescrever o código de rasterização novamente, mas sugiro que você mesmo implemente a texturização em sua renderização. O resultado deve ser a exibição correta das texturas no modelo. Aqui está o que eu tenho:







Todas as informações sobre as coordenadas de textura do modelo estão no arquivo OBJ. Para usar isso, aprenda o formato: formato OBJ.

Iluminação

Com as texturas, tudo ficou muito mais divertido, mas vai ser muito divertido quando implementarmos a iluminação da cena. Para simular uma iluminação "barata", usarei o modelo Phong .

Modelo Phong

Em geral, este método simula a presença de 3 componentes de iluminação: o fundo (ambiente), espalhado (difuso) e espelho (refletir). A soma desses três componentes acabará por simular o comportamento físico da luz.





Modelo Phong



Para calcular a iluminação Phong, precisamosdas normais de superfície, para isso eu as adicionei na classe Vertex. Onde podemos obter os valores desses normais? Não, não precisamos calcular nada. O fato é que editores 3D generosos frequentemente os consideram eles próprios e fornecem modelos junto com os dados no contexto do formato OBJ. Tendo analisado o arquivo de modelo, obtemos o valor normal para 3 vértices de cada polígono.





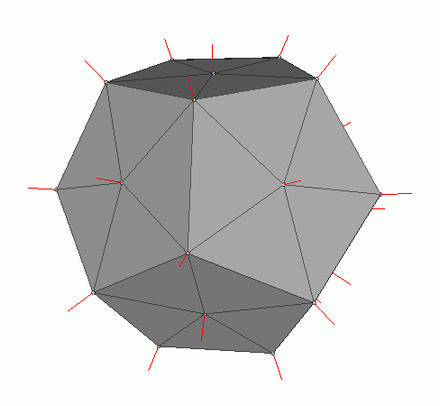
Imagem da wiki



Para calcular a normal em cada ponto do polígono, você precisa interpolar esses valores, já sabemos como fazer isso. Agora vamos dar uma olhada em todos os componentes para calcular a iluminação Phong.

Luz de fundo (ambiente)

Inicialmente, definimos a iluminação de fundo constante , para objetos não texturizados, você pode escolher qualquer cor para objetos com texturas Eu divido cada um dos componentes RGB em uma proporção de sombreamento básico (baseShading).

Luz difusa

Quando a luz atinge a superfície do polígono, ela é uniformemente espalhada. Para calcular o valor difuso em um pixel específico, o ângulo em que a luz atinge a superfície é levado em consideração . Para calcular este ângulo, você pode aplicar o produto escalar do raio incidente e o normal (é claro, os vetores devem ser normalizados antes disso). Este ângulo será multiplicado por um fator de intensidade de luz. Se o produto escalar for negativo, significa que o ângulo entre os vetores é maior que 90 graus. Nesse caso, começaremos a calcular não o clareamento, mas, ao contrário, o sombreamento. Vale a pena evitar este ponto, você pode fazer isso usando a função max .





Vamos aplicar luz difusa e dissipar a escuridão:

Luz do espelho (refletir)

Para calcular o componente espelho, você precisa levar em consideração o ponto de onde olhamos para o objeto . Agora vamos pegar o produto escalar do raio do observador e o raio refletido da superfície multiplicado pelo fator de intensidade da luz.





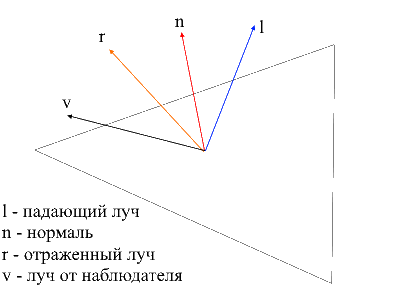
É fácil encontrar o raio do observador à superfície - será apenas a posição do vértice processado em coordenadas locais . Para encontrar o raio refletido, usei o seguinte método. O raio incidente pode ser decomposto em 2 vetores: sua projeção no normal e o segundo vetor, que pode ser encontrado subtraindo esta projeção do raio incidente. Para encontrar o raio refletido, você precisa subtrair o valor do segundo vetor da projeção para o normal.





Agora a imagem fica assim:

Sombras

O ponto final da minha apresentação será a implementação de sombras para renderização. A primeira ideia de beco sem saída que se originou em meu crânio é verificar para cada ponto se existe algum polígono entre ele e a luz . Se for, você não precisa iluminar o pixel. O modelo de Sylvanas contém mais de 220k polígonos. Se sim, para cada ponto para verificar a interseção com todos esses polígonos, você precisa fazer no máximo 220000 * 1920 * 1080 * 219999 chamadas para o método de interseção! Em 10 minutos meu computador foi capaz de dominar a décima parte de todos os cálculos (2600 polígonos de 220.000), após o que tive um turno e fui em busca de um novo método.



Na Internet, encontrei uma forma muito simples e bonita que realiza os mesmos cálculosmilhares de vezes mais rápido . É chamado de mapeamento de sombra (construção de um mapa de sombra). Lembre-se de como determinamos os pontos visíveis para o observador - usamos zbuffer . O mapeamento de sombra faz o mesmo! Na primeira passagem, nossa câmera estará na posição leve e olhando para o objeto. Isso irá gerar um mapa de profundidade para a fonte de luz. O mapa de profundidade é o conhecido zbuffer. Na segunda passagem, usamos este mapa para determinar quais vértices devem ser iluminados. Agora vou quebrar as regras de um bom código e seguir o caminho do cheat - acabo de passar um novo objeto rasterizador para o shader e usá-lo para criar um mapa de profundidade para nós.





Para uma cena estática, bastará chamar a construção do mapa de profundidade uma vez e, em seguida, utilizá-lo em todos os frames. Como teste, estou usando um modelo menos poligonal da arma. Esta é a imagem de saída:







Muitos de vocês provavelmente notaram os artefatos desse sombreador (pontos pretos não processados ​​pela luz). Novamente, voltando-me para a rede onisciente, encontrei uma descrição desse efeito com o nome desagradável de "acne sombra" (perdoem-me as pessoas com uma aparência complexa). A essência dessas "lacunas" é que usamos a resolução limitada do mapa de profundidade para definir a sombra. Isso significa que vários vértices ao renderizar recebem um valor do mapa de profundidade. Os mais suscetíveis a esse artefato são as superfícies nas quais a luz incide em um ângulo suave . O efeito pode ser corrigido aumentando a resolução de renderização das luzes, mas há uma maneira mais elegante . Consiste em adicionarum deslocamento específico para a profundidade dependendo do ângulo entre o feixe de luz e a superfície . Isso pode ser feito usando o produto escalar.

Conclusão

Eu me considero um iniciante em gráficos 3D, não excluo os erros que cometi no decorrer da apresentação. A única coisa em que conto é o resultado prático obtido no processo de criação. Você pode deixar todas as correções e otimizações (se houver) nos comentários, ficarei feliz em lê-los. Link para o repositório do projeto .