1.1 O que é árvore de decisão?
1.1.1 Exemplo de árvore de decisão
Por exemplo, temos o seguinte conjunto de dados (conjunto de datas): clima, temperatura, umidade, vento, golfe. Dependendo do tempo e de tudo mais, íamos (〇) ou não (×) jogávamos golfe. Vamos supor que temos 14 opções pré-concebidas.
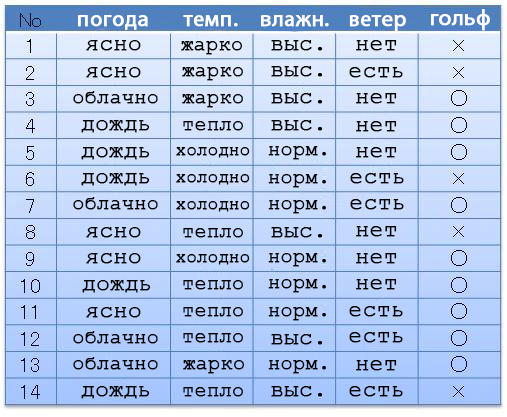
A partir desses dados, podemos compor uma estrutura de dados mostrando em quais casos fomos jogar golfe. Essa estrutura é chamada de Árvore de Decisão devido à sua forma ramificada.
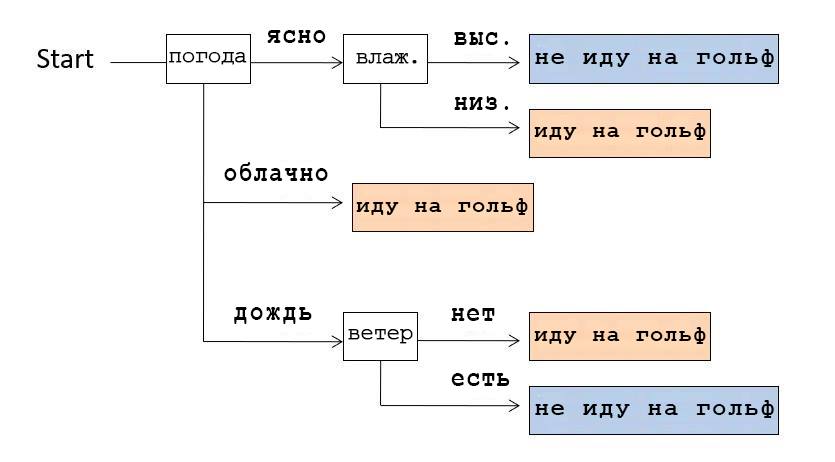
Por exemplo, se olharmos para a Árvore de Decisão mostrada na imagem acima, percebemos que verificamos o tempo primeiro. Se estava claro, verificamos a umidade: se estiver alta, então não vamos jogar golfe, se estiver baixa, vamos. E se o tempo estivesse nublado, iam jogar golfe, independentemente das outras condições.
1.1.2 Sobre este artigo
Existem algoritmos que criam tais Árvores de Decisão automaticamente com base nos dados disponíveis. Neste artigo, usaremos o algoritmo ID3 em Python.
Este artigo é o primeiro de uma série. Os seguintes artigos:
(Nota do tradutor: “se você está interessado na sequência, por favor nos avise nos comentários.”)
- Fundamentos da programação Python
- Noções básicas de biblioteca essenciais para análise de dados do Pandas
- Noções básicas de estrutura de dados (no caso da árvore de decisão)
- Noções básicas de entropia de informação
- Aprender um algoritmo para gerar uma árvore de decisão
1.1.3 Um pouco sobre a Árvore de Decisão
A geração da árvore de decisão está relacionada ao aprendizado de máquina supervisionado e à classificação. A classificação no aprendizado de máquina é uma forma de criar um modelo que leve à resposta correta com base no treinamento na data definida com as respostas corretas e os dados que levam a elas. O Deep Learning, que tem se tornado muito popular nos últimos anos, principalmente na área de reconhecimento de imagem, também faz parte do aprendizado de máquina baseado no método de classificação. A diferença entre Deep Learning e Decision Tree é se o resultado final é reduzido a uma forma na qual uma pessoa entende os princípios de geração da estrutura de dados final. A peculiaridade do Deep Learning é que obtemos o resultado final, mas não entendemos o princípio de sua geração. Ao contrário do Deep Learning, a árvore de decisão é fácil de entender por humanos, o que também é um recurso importante.
Esse recurso da árvore de decisão é bom não apenas para aprendizado de máquina, mas também para mineração de dados, onde a compreensão dos dados pelo usuário também é importante.
1.2 Sobre o algoritmo ID3
ID3 é um algoritmo de geração de árvore de decisão desenvolvido em 1986 por Ross Quinlan. Possui dois recursos importantes:
- Dados categóricos. Esses dados são semelhantes ao nosso exemplo acima (vá jogar golfe ou não), dados com um rótulo categórico específico. ID3 não pode usar dados numéricos.
- A entropia da informação é um indicador que indica uma sequência de dados com a menor variância das propriedades de uma classe de valores.
1.2.1 Sobre o uso de dados numéricos
O algoritmo C4.5, que é uma versão mais avançada do ID3, pode usar dados numéricos, mas como a ideia básica é a mesma nesta série, usaremos o ID3 primeiro.
1.3 Ambiente de desenvolvimento
O programa que descrevi abaixo, testei e executei nas seguintes condições:
- Notebooks Jupyter (usando Notebooks Azure)
- Python 3.6
- Bibliotecas: matemática, pandas, functools (não usei scikit-learn, tensorflow, etc.)
1.4 Programa de amostra
1.4.1 Na verdade, o programa
Primeiro, vamos copiar o programa para o Jupyter Notebook e executá-lo.
import math
import pandas as pd
from functools import reduce
#
d = {
"":["","","","","","","","","","","","","",""],
"":["","","","","","","","","","","","","",""],
"":["","","","","","","","","","","","","",""],
"":["","","","","","","","","","","","","",""],
# - , ,
# .
"":["×","×","○","○","○","×","○","×","○","○","○","○","○","×"],
}
df0 = pd.DataFrame(d)
# - , - pandas.Series,
# -
# s value_counts() ,
# , , items().
# , sorted,
#
# , , : (k) (v).
cstr = lambda s:[k+":"+str(v) for k,v in sorted(s.value_counts().items())]
# Decision Tree
tree = {
# name: ()
"name":"decision tree "+df0.columns[-1]+" "+str(cstr(df0.iloc[:,-1])),
# df: , ()
"df":df0,
# edges: (), ,
# , .
"edges":[],
}
# , , open
open = [tree]
# - .
# - pandas.Series、 -
entropy = lambda s:-reduce(lambda x,y:x+y,map(lambda x:(x/len(s))*math.log2(x/len(s)),s.value_counts()))
# , open
while(len(open)!=0):
# open ,
# ,
n = open.pop(0)
df_n = n["df"]
# , 0,
#
if 0==entropy(df_n.iloc[:,-1]):
continue
# ,
attrs = {}
# ,
for attr in df_n.columns[:-1]:
# , ,
# , .
attrs[attr] = {"entropy":0,"dfs":[],"values":[]}
# .
# , sorted ,
# , .
for value in sorted(set(df_n[attr])):
#
df_m = df_n.query(attr+"=='"+value+"'")
# ,
attrs[attr]["entropy"] += entropy(df_m.iloc[:,-1])*df_m.shape[0]/df_n.shape[0]
attrs[attr]["dfs"] += [df_m]
attrs[attr]["values"] += [value]
pass
pass
# , ,
# .
if len(attrs)==0:
continue
#
attr = min(attrs,key=lambda x:attrs[x]["entropy"])
#
# , , open.
for d,v in zip(attrs[attr]["dfs"],attrs[attr]["values"]):
m = {"name":attr+"="+v,"edges":[],"df":d.drop(columns=attr)}
n["edges"].append(m)
open.append(m)
pass
#
print(df0,"\n-------------")
# , - tree: ,
# indent: indent,
# - .
# .
def tstr(tree,indent=""):
# .
# ( 0),
# df, , .
s = indent+tree["name"]+str(cstr(tree["df"].iloc[:,-1]) if len(tree["edges"])==0 else "")+"\n"
# .
for e in tree["edges"]:
# .
# indent .
s += tstr(e,indent+" ")
pass
return s
# .
print(tstr(tree))1.4.2 Resultado
Se você executar o programa acima, nossa Árvore de Decisão será representada como uma tabela de símbolos conforme mostrado abaixo.
decision tree ['×:5', '○:9']
=
=['○:2']
=['×:3']
=['○:4']
=
=['×:2']
=['○:3']
1.4.3 Alterar os atributos (matrizes de dados) que queremos explorar
O último array no conjunto de datas d é um atributo de classe (o array de dados que queremos classificar).
d = {
"":["","","","","","","","","","","","","",""],
"":["","","","","","","","","","","","","",""],
"":["","","","","","","","","","","","","",""],
"":["×","×","○","○","○","×","○","×","○","○","○","○","○","×"],}
# - , , .
"":["","","","","","","","","","","","","",""],
}Por exemplo, se você trocar as matrizes "Golf" e "Wind", conforme mostrado no exemplo acima, obterá o seguinte resultado:
decision tree [':6', ':8']
=×
=
=
=[':1', ':1']
=[':1']
=[':2']
=○
=
=[':1']
=[':1']
=
=[':2']
=[':1']
=[':1']
=[':3']Em essência, criamos uma regra na qual dizemos ao programa para se ramificar primeiro pela presença e ausência de vento e se vamos jogar golfe ou não.
Obrigado por ler!
Ficaremos muito felizes se você nos contar se gostou deste artigo, a tradução foi clara, foi útil para você?