
Fonte: Vecteezy
Sim, a regressão linear não é a única. Cite
rapidamente cinco algoritmos de aprendizado de máquina.
É improvável que você nomeie muitos algoritmos de regressão. Afinal, o único algoritmo de regressão amplamente utilizado é a regressão linear, principalmente por causa de sua simplicidade. No entanto, a regressão linear é freqüentemente inaplicável a dados reais devido a opções muito limitadas e liberdade de manobra limitada. Muitas vezes, é usado apenas como um modelo básico para avaliação e comparação com novas abordagens de pesquisa.
Equipe de soluções em nuvem Mail.rutraduziu um artigo, o autor do qual descreve 5 algoritmos de regressão. Vale a pena tê-los em sua caixa de ferramentas, juntamente com algoritmos de classificação populares, como SVM, árvore de decisão e redes neurais.
1. Regressão da rede neural
Teoria
As redes neurais são incrivelmente poderosas, mas são comumente usadas para classificação. Os sinais viajam através de camadas de neurônios e são generalizados em uma das várias classes. No entanto, eles podem ser adaptados rapidamente em modelos de regressão, alterando a última função de ativação.
Cada neurônio transmite valores da conexão anterior por meio de uma função de ativação que serve ao propósito de generalização e não linearidade. Normalmente, a função de ativação é algo como uma função sigmóide ou ReLU (unidade linear retificada).
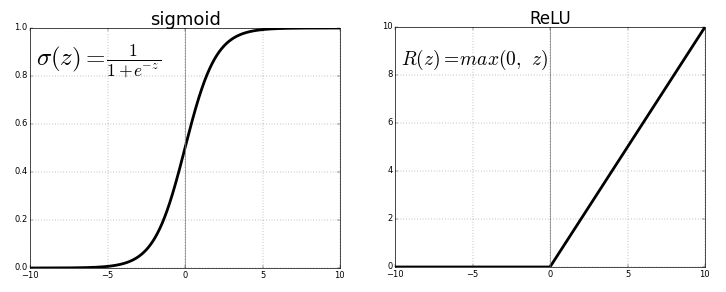
Fonte . Imagem livre
Mas, substituindo a última função de ativação (neurônio de saída) por uma lineara função de ativação, o sinal de saída pode ser mapeado para muitos valores fora das classes fixas. Assim, a saída não será a probabilidade de atribuir o sinal de entrada a qualquer classe, mas um valor contínuo no qual a rede neural fixa suas observações. Nesse sentido, podemos dizer que a rede neural complementa a regressão linear.
A regressão da rede neural tem a vantagem da não linearidade (além da complexidade) que pode ser introduzida com sigmóide e outras funções de ativação não linear anteriormente na rede neural. No entanto, o uso excessivo de ReLU como uma função de ativação pode significar que o modelo tende a evitar a saída de valores negativos, uma vez que ReLU ignora as diferenças relativas entre os valores negativos.
Isso pode ser resolvido limitando o uso de ReLU e adicionando mais valores negativos das funções de ativação correspondentes ou normalizando os dados para uma faixa estritamente positiva antes do treinamento.
Implementação
Usando Keras, vamos construir uma estrutura de rede neural artificial, embora o mesmo possa ser feito com uma rede neural convolucional ou outra rede se a última camada for uma camada densa com ativação linear ou apenas uma camada com ativação linear. ( Observe que as importações de Keras não são listadas para economizar espaço ).
model = Sequential()
model.add(Dense(100, input_dim=3, activation='sigmoid'))
model.add(ReLU(alpha=1.0))
model.add(Dense(50, activation='sigmoid'))
model.add(ReLU(alpha=1.0))
model.add(Dense(25, activation='softmax'))
#IMPORTANT PART
model.add(Dense(1, activation='linear'))
O problema com as redes neurais sempre foi sua alta variância e tendência ao ajuste excessivo. Existem muitas fontes de não linearidade no exemplo de código acima, como SoftMax ou sigmóide.
Se sua rede neural faz um bom trabalho com dados de treinamento com uma estrutura puramente linear, pode ser melhor usar a regressão de árvore de decisão truncada, que emula uma rede neural linear e altamente dispersa, mas permite que o cientista de dados tenha melhor controle sobre profundidade, largura e outros atributos para controlar o sobreajuste.
2. Regressão da árvore de decisão
Teoria
As árvores de decisão na classificação e na regressão são muito semelhantes, pois trabalham construindo árvores com nós sim / não. No entanto, enquanto os nós folha de classificação resultam em um único valor de classe (por exemplo, 1 ou 0 para um problema de classificação binária), as árvores de regressão acabam com um valor no modo contínuo (por exemplo, 4593,49 ou 10,98).
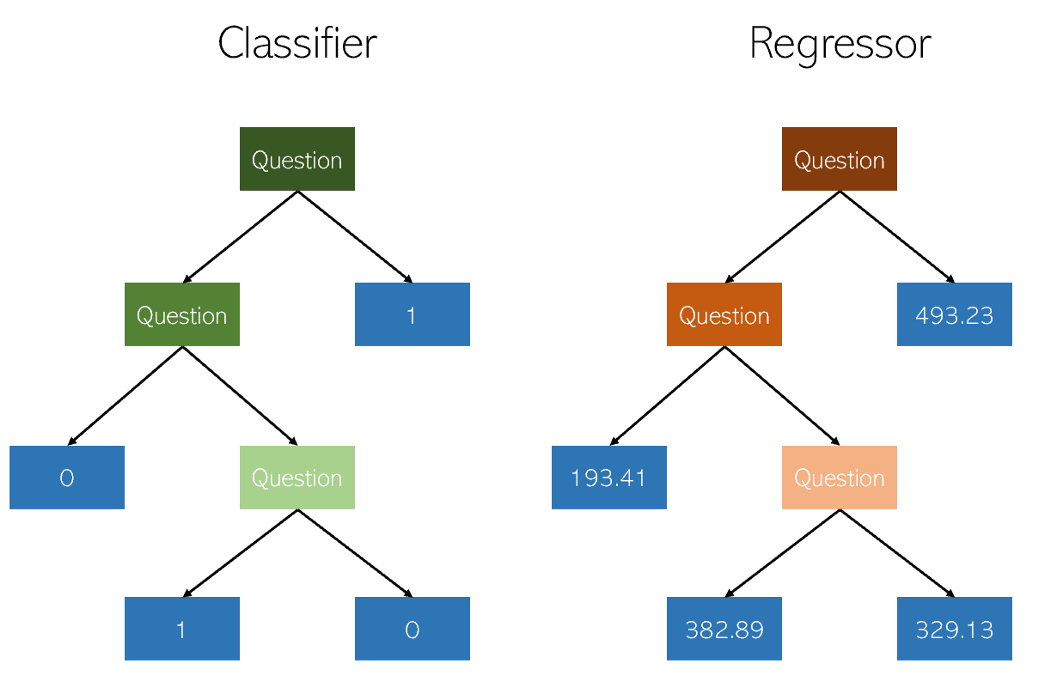
Ilustração do autor
Devido à natureza específica e altamente dispersa da regressão como um problema simples de aprendizado de máquina, os regressores de árvore de decisão devem ser cuidadosamente podados. No entanto, a abordagem de regressão é irregular - em vez de calcular o valor em uma escala contínua, ela chega a determinados nós finais. Se o regressor for cortado demais, ele terá poucos nós de folha para cumprir seu propósito adequadamente.
Consequentemente, a árvore de decisão deve ser podada para que tenha mais liberdade (os valores de saída possíveis da regressão são o número de nós folha), mas não o suficiente para ser muito profunda. Se você não o cortar, o algoritmo já altamente disperso se tornará excessivamente complexo devido à natureza da regressão.
Implementação
A regressão da árvore de decisão pode ser facilmente criada em
sklearn:
from sklearn.tree import DecisionTreeRegressor
model = DecisionTreeRegressor()
model.fit(X_train, y_train)
Uma vez que os parâmetros do regressor da árvore de decisão são muito importantes, é recomendável usar uma ferramenta de otimização de mecanismo de pesquisa de parâmetros
GridCVde sklearn, para encontrar a recomendação certa para este modelo.
Ao avaliar formalmente o desempenho, use o teste em
K-foldvez do teste padrão train-test-splitpara evitar a aleatoriedade do último, que pode violar os resultados sensíveis do modelo de alta variação.
Bônus: Um parente próximo da árvore de decisão, o algoritmo de floresta aleatório, também pode ser implementado como um regressor. Um regressor de floresta aleatório pode ou não ter um desempenho melhor do que uma árvore de decisão na regressão (embora geralmente tenha um desempenho melhor na classificação) devido ao delicado equilíbrio entre redundância e inadequação nos algoritmos de construção de árvore.
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor()
model.fit(X_train, y_train)
3. Regressão LASSO
O método de regressão lasso (LASSO, Least Absolute Shrinkage and Selection Operator) é uma variação da regressão linear especialmente adaptada para dados que exibem forte multicolinearidade (isto é, forte correlação de recursos entre si).
Ele automatiza partes da seleção de modelo, como seleção de variável ou exclusão de parâmetro. O LASSO usa encolhimento, que é um processo no qual os valores dos dados se aproximam de um ponto central (como uma média).

Ilustração do autor. Visualização simplificada do
processo de compressão O processo de compressão adiciona várias vantagens aos modelos de regressão:
- Estimativas mais precisas e estáveis de parâmetros verdadeiros.
- Reduzindo erros de amostragem e fora de amostragem.
- Suavização de flutuações espaciais.
Em vez de ajustar a complexidade do modelo para compensar a complexidade dos dados, como rede neural de alta variância e métodos de regressão de árvore de decisão, o laço tenta reduzir a complexidade dos dados para que possam ser tratados por métodos de regressão simples curvando o espaço em que se encontram. Nesse processo, o laço ajuda automaticamente a eliminar ou distorcer recursos altamente correlacionados e redundantes em um método de baixa variação.
A regressão Lasso usa regularização L1, ou seja, pondera os erros por seu valor absoluto. Em vez de, por exemplo, a regularização L2, que pondera os erros pelo quadrado, para punir os erros mais significativos com mais força.
Essa regularização geralmente leva a modelos mais esparsos com menos coeficientes, pois alguns coeficientes podem se tornar zero e, portanto, ser excluídos do modelo. Isso permite que seja interpretado.
Implementação
O
sklearnlaço de regressão vem com um modelo de validação cruzada que seleciona o mais eficaz dos muitos modelos treinados com diferentes parâmetros fundamentais e caminhos de aprendizagem que automatizam uma tarefa que, de outra forma, teria que ser executada manualmente.
from sklearn.linear_model import LassoCV
model = LassoCV()
model.fit(X_train, y_train)
4. Regressão de cume (regressão de cume)
Teoria
A regressão de cume ou regressão de cume é muito semelhante à regressão de LASSO no sentido de que aplica compressão. Ambos os algoritmos são adequados para conjuntos de dados com um grande número de recursos que não são independentes um do outro (colinearidade).
Porém, a maior diferença entre eles é que a regressão crista usa a regularização L2, ou seja, nenhum dos coeficientes não se torna zero, como a regressão LASSO. Em vez disso, os coeficientes estão cada vez mais próximos de zero, mas têm pouco incentivo para alcançá-lo devido à natureza da regularização de L2.
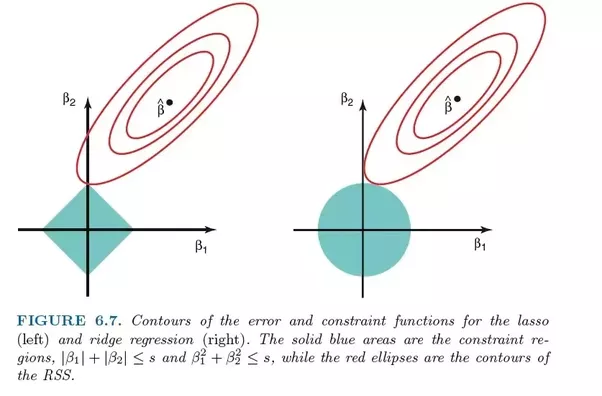
Comparação de erros na regressão laço (esquerda) e regressão crista (direita). Como o Ridge Regression usa a regularização L2, sua área se assemelha a um círculo, enquanto a regularização do laço L1 desenha linhas retas. Imagem grátis. Fonte
No laço, a melhoria do erro 5 para o erro 4 é ponderada da mesma forma que a melhoria de 4 para 3, e também de 3 para 2, de 2 para 1 e de 1 para 0. Portanto, mais coeficientes chegam a zero e mais recursos são eliminados.
No entanto, na regressão de crista, a melhora do erro 5 para o erro 4 é calculada como 5² - 4² = 9, enquanto a melhora de 4 para 3 é ponderada apenas como 7. Gradualmente, a recompensa pela melhora diminui; portanto, menos recursos são eliminados.
A regressão Ridge é mais adequada para situações em que desejamos priorizar um grande número de variáveis, cada uma com um pequeno efeito. Se o seu modelo precisar levar em consideração várias variáveis, cada uma delas com um efeito médio a grande, o laço é a melhor escolha.
Implementação
A regressão Ridge
sklearnpode ser implementada da seguinte forma (veja abaixo). Tal como acontece com a regressão laço, sklearnhá uma implementação para validar cruzadamente a seleção do melhor de muitos modelos treinados.
from sklearn.linear_model import RidgeCV
model = Ridge()
model.fit(X_train, y_train)
5. Regressão ElasticNet
Teoria
ElasticNet tem como objetivo combinar o melhor de Ridge Regression e Lasso Regression combinando a regularização L1 e L2.
Lasso e Ridge Regression são dois métodos de regularização diferentes. Em ambos os casos, λ é o fator-chave que controla o tamanho da multa:
- λ = 0, , .
- λ = ∞, - . , , .
- 0 < λ < ∞, λ , .
Ao parâmetro λ, a regressão ElasticNet adiciona um parâmetro adicional α , que mede o quão "misturadas" as regularizações L1 e L2 deveriam ser. Quando α é 0, o modelo é pura regressão de crista, e quando α é 1, é pura regressão laço.
A “razão de mistura” α simplesmente determina o quanto de regularização L1 e L2 deve ser considerada na função de perda. Todos os três modelos de regressão populares - Ridge, Lasso e ElasticNet - visam reduzir o tamanho de seus coeficientes, mas cada um age de maneira diferente.
Implementação
ElasticNet pode ser implementado usando o modelo de validação cruzada do sklearn:
from sklearn.linear_model import ElasticNetCV
model = ElasticNetCV()
model.fit(X_train, y_train)
O que mais ler sobre o assunto:
- Analisando Big Data na nuvem: como uma empresa pode se tornar orientada a dados.
- Formatos de arquivo em big data.
- - .