📣 👋🏻 👓 TensorFlow.js: parte 1: usando a API de baixo nível para aproximar funções lineares ⚠️ 🅾️ 🎢

Python atualmente detém a posição dominante em aprendizado de máquina. No entanto, se você é um desenvolvedor JS e está interessado em mergulhar neste mundo, não é necessário incluir uma nova linguagem de programação em seu arsenal, devido ao advento do TensorFlow.js .

Benefícios de usar TensorFlow.js em um navegador

interatividade - o navegador possui diversas ferramentas de visualização dos processos em andamento (gráficos, animação, etc.);
sensores - o navegador tem acesso direto aos sensores do dispositivo (câmera, GPS, acelerômetro, etc.);
segurança dos dados do usuário - não há necessidade de enviar os dados processados para o servidor;
compatibilidade com modelos criados em Python .

atuação

Um dos principais problemas é o desempenho.

Devido ao fato de que o aprendizado de máquina está, na verdade, realizando vários tipos de operações matemáticas com dados do tipo matriz (tensores), a biblioteca para este tipo de cálculos no navegador usa WebGL. Isso melhora significativamente o desempenho se as mesmas operações forem realizadas em JS puro. Naturalmente, a biblioteca tem um fallback caso o WebGL não seja suportado no navegador por algum motivo (no momento da redação deste artigo, caniuse mostrava que 97,94% dos usuários tinham suporte ao WebGL).

Para melhorar o desempenho, o Node.js usa ligação nativa com TensorFlow. Aqui, CPU, GPU e TPU ( unidade de processamento de tensor ) podem servir como aceleradores

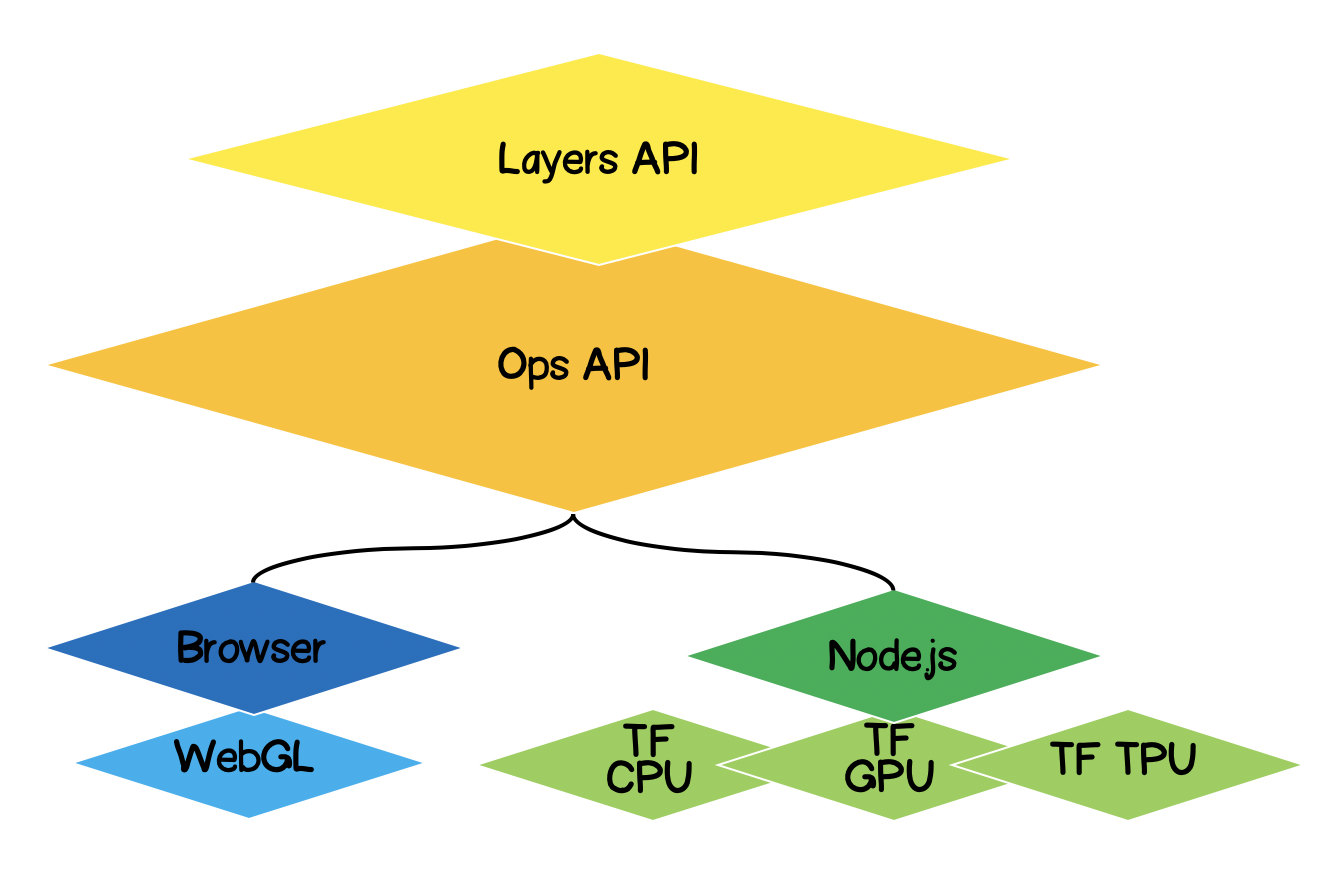
Arquitetura TensorFlow.js

Camada mais baixa - esta camada é responsável pela paralelização dos cálculos ao realizar operações matemáticas em tensores.
A API Ops - fornece uma API para realizar operações matemáticas em tensores.
API de camadas - permite criar modelos complexos de redes neurais usando diferentes tipos de camadas (densas, convolucionais). Essa camada é semelhante à API Keras Python e tem a capacidade de carregar redes baseadas em Keras Python pré-treinadas.

Formulação do problema

É necessário encontrar a equação da função linear de aproximação para um determinado conjunto de pontos experimentais. Em outras palavras, precisamos encontrar uma curva linear que fique mais próxima dos pontos experimentais.

Formalização da solução

O núcleo de qualquer aprendizado de máquina será um modelo, no nosso caso, esta é a equação de uma função linear:

y = k x + b

Com base na condição, também temos um conjunto de pontos experimentais:

(x_{t}^{(0)}, y_{t}^{(0)}), (x_{t}^{(1)}, y_{t}^{(1)}), . . . (x_{t}^{(N)}, y_{t}^{(N)})

Suponha que em

j

etapa de treinamento, os seguintes coeficientes da equação linear foram calculados

k^{(j)}, b^{(j)}

. Agora precisamos expressar matematicamente quão precisos são os coeficientes selecionados. Para fazer isso, precisamos calcular o erro (perda), que pode ser determinado, por exemplo, pelo desvio padrão. Tensorflow.js oferece um conjunto de funções de perda comumente usadas:tf.metrics.meanAbsoluteError,tf.metrics.meanSquaredErrore outras.

L (k^{(j)}, b^{(j)}) = \sum_{i = 1}^{N} (y_{p r e d i c t e d}^{(i)} - y_{t}^{(i)})^{2} = \sum_{i = 1}^{N} ((k^{(j)} \cdot x^{(i)} + b^{(j)}) - y_{t}^{(i)})

O objetivo da aproximação é minimizar a função de erro

L

. Vamos usar o método gradiente descendente para isso. É necessário:

- encontre o vetor gradiente calculando as derivadas parciais em relação aos coeficientes $k^{(j)}, b^{(j)}$ ;
- corrija os coeficientes da equação na direção oposta à direção do vetor gradiente. Assim, iremos minimizar a função de erro:

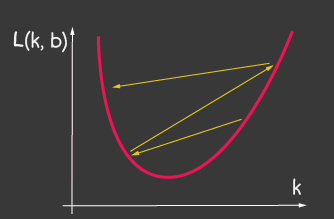
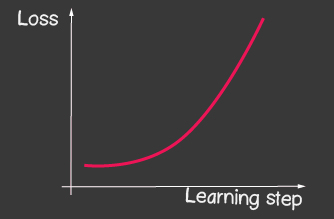
$k^{(j + 1)} = k^{(j)} - μ ▽_{k^{(j)}} L (k^{(j)}, b^{(j)}) = k^{(j)} - μ \frac{\partial L (k^{(j)}, b^{(j)})}{\partial k^{(j)}};$

$b^{(j + 1)} = b^{(j)} - μ ▽_{b^{(j)}} L (k^{(j)}, b^{(j)}) = b^{(j)} - μ \frac{\partial L (k^{(j)}, b^{(j)})}{\partial b^{(j)}};$

$μ$ é a taxa de aprendizado e é um dos parâmetros ajustáveis do modelo. Para descida de gradiente, ele não muda ao longo do processo de aprendizagem. Um pequeno valor da taxa de aprendizado pode levar a uma longa convergência do processo de aprendizado do modelo e um possível acerto no mínimo local (Figura 2), e um valor muito grande pode levar a um aumento infinito no valor do erro em cada etapa do treinamento, Figura 1.


Figura 1: O alto valor da taxa de aprendizagem	Figura 2: pequena taxa de aprendizagem

Como implementá-lo sem Tensorflow.js

Por exemplo, calcular o valor da função de perda (desvio padrão) ficaria assim:

function loss(ysPredicted, ysReal) {
    const squaredSum = ysPredicted.reduce(
        (sum, yPredicted, i) => sum + (yPredicted - ysReal[i]) ** 2,
        0);
    return squaredSum / ysPredicted.length;
}

No entanto, a quantidade de dados de entrada pode ser grande. Ao treinar o modelo, precisamos calcular não apenas o valor da função de perda em cada iteração, mas também realizar operações mais sérias - calcular o gradiente. Portanto, faz sentido usar tensorflow, que otimiza cálculos usando WebGL. Além disso, o código se torna muito mais expressivo, compare:

    function loss(ysPredicted, ysReal) => {
        const ysPredictedTensor = tf.tensor(ysPredicted);
        const ysRealTensor = tf.tensor(ysReal);
        const loss = ysPredictedTensor.sub(ysRealTensor).square().mean();
        return loss.dataSync()[0];
    };

Solução com TensorFlow.js

A boa notícia é que não teremos que escrever otimizadores para uma dada função de erro (perda), não desenvolveremos métodos numéricos para calcular derivadas parciais, já implementamos o algoritmo de retropropogação para nós. Precisamos apenas seguir estas etapas:

definir um modelo (uma função linear, no nosso caso);
descreva a função de erro (no nosso caso, este é o desvio padrão)
escolha um dos otimizadores implementados (é possível estender a biblioteca com sua própria implementação)

O que é tensor

Absolutamente todo mundo já encontrou tensores na matemática - estes são escalares, vetoriais, matriz 2D, matriz 3D. Um tensor é um conceito generalizado de todos os itens acima. Este é um contêiner de dados que contém dados de um tipo homogêneo (tensorflow suporta int32, float32, bool, complex64, string) e tem uma forma específica (o número de eixos (classificação) e o número de elementos em cada um dos eixos). A seguir consideraremos tensores até matrizes 3D, mas como se trata de uma generalização, um tensor pode ter quantos eixos quisermos: 5D, 6D, ... ND.

O TensorFlow tem a seguinte API para geração de tensor:

tf.tensor (values, shape?, dtype?)

onde forma é a forma do tensor e é dada por uma matriz, em que o número de elementos é o número de eixos, e cada valor da matriz determina o número de elementos ao longo de cada um dos eixos. Por exemplo, para definir uma matriz 4x2 (4 linhas, 2 colunas), a forma assumirá a forma [4, 2].

Visualização	Descrição
	Classificação escalar : 0 Forma: [] estrutura JS: `2` API TensorFlow: `tf.scalar(2); tf.tensor(2, []);`
	Classificação do vetor : 1 Forma: [4] Estrutura JS: `[1, 2, 3, 4]` API TensorFlow: `tf.tensor([ 1, 2, 3, 4]); tf.tensor([1, 2, 3, 4], [4]); tf.tensor1d([1, 2, 3, 4]);`
	Classificação da matriz : 2 Forma: [4,2] Estrutura JS: `[ [1, 2], [3, 4], [5, 6], [7, 8] ]` API TensorFlow: `tf.tensor([[1, 2],[3, 4],[5,6],[7,8]]); tf.tensor([1, 2, 3, ... 7, 8], [4,2]); tf.tensor2d([[1, 2],[3, 4]...[7,8]]); tf.tensor2d([1, 2, 3, ... 7, 8], [4,2]);`
	Classificação da matriz : 3 Forma: [4,2,3] Estrutura JS: `[ [ [ 1, 2], [ 3, 4], [ 5, 6] ], [ [ 7, 8], [ 9, 10], [11, 12] ], [ [13, 14], [15, 16], [17, 18] ], [ [19, 20], [21, 22], [23, 24] ] ]` API TensorFlow: `tf.tensor([ [ [ 1, 2], [ 3, 4], [ 5, 6] ], .... [ [19, 20], [21, 22], [23, 24] ] ]); tf.tensor([1, 2, 3, .... 24], [4, 2 ,3])`

Aproximação linear com TensorFlow.js

Inicialmente, falaremos sobre como tornar o código extensível. Podemos transformar a aproximação linear em uma aproximação dos pontos experimentais por uma função de qualquer tipo. A hierarquia de classes ficará assim:

Vamos começar a implementar os métodos da classe abstrata, com exceção dos métodos abstratos que serão definidos nas classes filhas, e aqui só deixaremos stubs com erros se por algum motivo o método não for definido na classe filha.

import * as tf from '@tensorflow/tfjs';

export default class AbstractRegressionModel {
    constructor(
        width,
        height,
        optimizerFunction = tf.train.sgd,
        maxEpochPerTrainSession = 100,
        learningRate = 0.1,
        expectedLoss = 0.001
    ) {
        this.width = width;
        this.height = height;
        this.optimizerFunction = optimizerFunction;
        this.expectedLoss = expectedLoss;
        this.learningRate = learningRate;
        this.maxEpochPerTrainSession = maxEpochPerTrainSession;

        this.initModelVariables();

        this.trainSession = 0;
        this.epochNumber = 0;
        this.history = [];
    }
}

Assim, no construtor do modelo definimos largura e altura - estas são a largura e altura reais do plano em que colocaremos os pontos experimentais. Isso é necessário para normalizar os dados de entrada. Essa. se tiver-mos

x \in [0, w i d t h], y \in [0, h e i g h t]

, então após a normalização teremos:

x_{n o r m} \in [0, 1], y_{n o r m} \in [0, 1]

optimizerFunction - vamos tornar a tarefa do otimizador flexível, para poder experimentar outros otimizadores disponíveis na biblioteca, por padrão definimos o método Stochastic Gradient Descent tf.train.sgd . Eu também recomendaria jogar com outros otimizadores disponíveis que podem ajustar o learningRate durante o treinamento e o processo de aprendizado é muito melhorado, por exemplo, tente os seguintes otimizadores: tf.train.momentum , tf.train.adam .

Para que o processo de aprendizagem não indefinidamente, definimos dois parâmetros maxEpochPerTrainSesion e expectedLoss- desta forma, pararemos o processo de treinamento ou quando o número máximo de iterações de treinamento for atingido, ou quando o valor da função de erro for inferior ao erro esperado (levaremos tudo em consideração no método de treinamento abaixo).

No construtor, chamamos o método initModelVariables - mas, conforme combinado, fazemos o stub e o definimos na classe filha posteriormente.

initModelVariables() {
    throw Error('Model variables should be defined')
}

Agora vamos implementar o método principal do modelo de trem:

/**
     * Train model until explicitly stop process via invocation of stop method
     * or loss achieve necessary accuracy, or train achieve max epoch value
     *
     * @param x - array of x coordinates
     * @param y - array of y coordinates
     * @param callback - optional, invoked after each training step
     */
    async train(x, y, callback) {
        const currentTrainSession = ++this.trainSession;
        this.lossVal = Number.POSITIVE_INFINITY;
        this.epochNumber = 0;
        this.history = [];

        // convert array into tensors
        const input = tf.tensor1d(this.xNormalization(x));
        const output = tf.tensor1d(this.yNormalization(y));

        while (
            currentTrainSession === this.trainSession
            && this.lossVal > this.expectedLoss
            && this.epochNumber <= this.maxEpochPerTrainSession
            ) {
            const optimizer = this.optimizerFunction(this.learningRate);
            optimizer.minimize(() => this.loss(this.f(input), output));
            this.history = [...this.history, {
                epoch: this.epochNumber,
                loss: this.lossVal
            }];
            callback && callback();
            this.epochNumber++;
            await tf.nextFrame();
        }
    }

trainSession é essencialmente um identificador único para a sessão de treinamento no caso de a API externa chamar o método train, enquanto a sessão de treinamento anterior ainda não terminou.

Pelo código, você pode ver que criamos tensor1d a partir de matrizes unidimensionais, enquanto os dados devem ser normalizados de antemão, as funções de normalização estão aqui:

xNormalization = xs => xs.map(x => x / this.width);
yNormalization = ys => ys.map(y => y / this.height);
yDenormalization = ys => ys.map(y => y * this.height);

Em um loop, para cada etapa de treinamento, chamamos o otimizador de modelo, para o qual precisamos passar a função de perda. Conforme combinado, a função de perda será definida pelo desvio padrão. Então, usando a API tensorflow.js, temos:

    /**
     * Calculate loss function as mean-square deviation
     *
     * @param predictedValue - tensor1d - predicted values of calculated model
     * @param realValue - tensor1d - real value of experimental points
     */
    loss = (predictedValue, realValue) => {
        // L = sum ((x_pred_i - x_real_i)^2) / N
        const loss = predictedValue.sub(realValue).square().mean();
        this.lossVal = loss.dataSync()[0];
        return loss;
    };

O processo de aprendizagem continua enquanto

o limite do número de iterações não será alcançado
a precisão de erro desejada não será alcançada
um novo processo de treinamento não foi iniciado

Observe também como a função de perda é chamada. Para obter predictedValue - chamamos a função f - que, de fato, vai definir a forma segundo a qual a regressão será realizada, e na classe abstrata, conforme combinado, colocamos um stub:

  f(x) {
        throw Error('Model should be defined')
  }

A cada etapa do treinamento, na propriedade do objeto do modelo histórico, salvamos a dinâmica da mudança do erro a cada época de treinamento.

Após o processo de treinamento do modelo, precisamos ter um método que aceite entradas e produza as saídas calculadas usando o modelo treinado. Para fazer isso, na API, definimos o método de previsão e se parece com isto:

/**
     * Predict value basing on trained model
     *  @param x - array of x coordinates
     *  @return Array({x: integer, y: integer}) - predicted values associated with input
     *
     * */
    predict(x) {
        const input = tf.tensor1d(this.xNormalization(x));
        const output = this.yDenormalization(this.f(input).arraySync());
        return output.map((y, i) => ({ x: x[i], y }));
    }

Preste atenção ao arraySync , por analogia com node.js, se houver um método arraySync , então definitivamente há um método de array assíncrono que retorna uma promessa. A promessa é necessária aqui, porque como dissemos anteriormente, os tensores são todos migrados para WebGL para acelerar os cálculos e o processo se torna assíncrono, porque leva tempo para mover os dados do WebGL para uma variável JS.

Terminamos com uma classe abstrata, você pode ver a versão completa do código aqui:

AbstractRegressionModel.js

import * as tf from '@tensorflow/tfjs';

export default class AbstractRegressionModel {
    
    constructor(
        width,
        height,
        optimizerFunction = tf.train.sgd,
        maxEpochPerTrainSession = 100,
        learningRate = 0.1,
        expectedLoss = 0.001
    ) {
        this.width = width;
        this.height = height;
        this.optimizerFunction = optimizerFunction;
        this.expectedLoss = expectedLoss;
        this.learningRate = learningRate;
        this.maxEpochPerTrainSession = maxEpochPerTrainSession;

        this.initModelVariables();

        this.trainSession = 0;
        this.epochNumber = 0;
        this.history = [];
    }

    initModelVariables() {
        throw Error('Model variables should be defined')
    }

    f() {
        throw Error('Model should be defined')
    }

    xNormalization = xs => xs.map(x => x / this.width);
    yNormalization = ys => ys.map(y => y / this.height);
    yDenormalization = ys => ys.map(y => y * this.height);

    /**
     * Calculate loss function as mean-squared deviation
     *
     * @param predictedValue - tensor1d - predicted values of calculated model
     * @param realValue - tensor1d - real value of experimental points
     */
    loss = (predictedValue, realValue) => {
        const loss = predictedValue.sub(realValue).square().mean();
        this.lossVal = loss.dataSync()[0];
        return loss;
    };

    /**
     * Train model until explicitly stop process via invocation of stop method
     * or loss achieve necessary accuracy, or train achieve max epoch value
     *
     * @param x - array of x coordinates
     * @param y - array of y coordinates
     * @param callback - optional, invoked after each training step
     */
    async train(x, y, callback) {
        const currentTrainSession = ++this.trainSession;
        this.lossVal = Number.POSITIVE_INFINITY;
        this.epochNumber = 0;
        this.history = [];

        // convert data into tensors
        const input = tf.tensor1d(this.xNormalization(x));
        const output = tf.tensor1d(this.yNormalization(y));

        while (
            currentTrainSession === this.trainSession
            && this.lossVal > this.expectedLoss
            && this.epochNumber <= this.maxEpochPerTrainSession
            ) {
            const optimizer = this.optimizerFunction(this.learningRate);
            optimizer.minimize(() => this.loss(this.f(input), output));
            this.history = [...this.history, {
                epoch: this.epochNumber,
                loss: this.lossVal
            }];
            callback && callback();
            this.epochNumber++;
            await tf.nextFrame();
        }
    }

    stop() {
        this.trainSession++;
    }

    /**
     * Predict value basing on trained model
     *  @param x - array of x coordinates
     *  @return Array({x: integer, y: integer}) - predicted values associated with input
     *
     * */
    predict(x) {
        const input = tf.tensor1d(this.xNormalization(x));
        const output = this.yDenormalization(this.f(input).arraySync());
        return output.map((y, i) => ({ x: x[i], y }));
    }
}

Para regressão linear, definimos uma nova classe que herdará da classe abstrata, onde precisamos apenas definir dois métodos initModelVariables e f .

Como estamos trabalhando em uma aproximação linear, devemos especificar duas variáveis k, b - e elas serão tensores escalares. Para o otimizador, devemos indicar que eles são personalizáveis (variáveis) e atribuir números arbitrários como valores iniciais.

initModelVariables() {
   this.k = tf.scalar(Math.random()).variable();
   this.b = tf.scalar(Math.random()).variable();
}

Considere a API para variável aqui :

tf.variable (initialValue, trainable?, name?, dtype?)

Preste atenção ao segundo argumento para treinável - uma variável booleana e por padrão é verdadeira . É utilizado por otimizadores, que informa se é necessário configurar esta variável ao minimizar a função de perda. Isso pode ser útil quando estamos construindo um novo modelo baseado em um modelo pré-treinado baixado de Keras Python, e estamos confiantes de que não há necessidade de retreinar algumas camadas neste modelo.

Em seguida, precisamos definir a equação da função de aproximação usando a API tensorflow, dê uma olhada no código e você entenderá intuitivamente como usá-lo:

f(x) {
   // y = kx + b
   return  x.mul(this.k).add(this.b);
}

Por exemplo, desta forma, você pode especificar uma aproximação quadrática:

initModelVariables() {
   this.a = tf.scalar(Math.random()).variable();
   this.b = tf.scalar(Math.random()).variable();
   this.c = tf.scalar(Math.random()).variable();
}

f(x) {
    // y = ax^2 + bx + c
    return this.a.mul(x.square()).add(this.b.mul(x)).add(this.c);
}

Aqui você pode verificar os modelos de regressão linear e quadrática:

LinearRegressionModel.js

import * as tf from '@tensorflow/tfjs';
import AbstractRegressionModel from "./AbstractRegressionModel";

export default class LinearRegressionModel extends AbstractRegressionModel {
    initModelVariables() {
        this.k = tf.scalar(Math.random()).variable();
        this.b = tf.scalar(Math.random()).variable();
    }

    f = x => x.mul(this.k).add(this.b);
}

QuadraticRegressionModel.js

import * as tf from '@tensorflow/tfjs';
import AbstractRegressionModel from "./AbstractRegressionModel";

export default class QuadraticRegressionModel extends AbstractRegressionModel {
    initModelVariables() {
        this.a = tf.scalar(Math.random()).variable();
        this.b = tf.scalar(Math.random()).variable();
        this.c = tf.scalar(Math.random()).variable();
    }

    f = x => this.a.mul(x.square()).add(this.b.mul(x)).add(this.c);
}

Abaixo está algum código escrito em React que usa o modelo de regressão linear escrito e cria a UX para o usuário:

Regression.js

import React, { useState, useEffect } from 'react';

import Canvas from './components/Canvas';
import LossPlot from './components/LossPlot_v3';
import LinearRegressionModel from './model/LinearRegressionModel';

import './RegressionModel.scss';

const WIDTH = 400;
const HEIGHT = 400;
const LINE_POINT_STEP = 5;

const predictedInput = Array.from({ length: WIDTH / LINE_POINT_STEP + 1 })
    .map((v, i) => i * LINE_POINT_STEP);

const model = new LinearRegressionModel(WIDTH, HEIGHT);

export default () => {
    const [points, changePoints] = useState([]);
    const [curvePoints, changeCurvePoints] = useState([]);
    const [lossHistory, changeLossHistory] = useState([]);

    useEffect(() => {
        if (points.length > 0) {
            const input = points.map(({ x }) => x);
            const output = points.map(({ y }) => y);

            model.train(input, output, () => {
                changeCurvePoints(() => model.predict(predictedInput));
                changeLossHistory(() => model.history);
            });
        }
    }, [points]);

    return (
        <div className="regression-low-level">
            <div className="regression-low-level__top">
                <div className="regression-low-level__workarea">
                    <div className="regression-low-level__canvas">
                        <Canvas
                            width={WIDTH}
                            height={HEIGHT}
                            points={points}
                            curvePoints={curvePoints}
                            changePoints={changePoints}
                        />
                    </div>
                    <div className="regression-low-level__toolbar">
                        <button
                            className="btn btn-red"
                            onClick={() => model.stop()}>Stop
                        </button>
                        <button
                            className="btn btn-yellow"
                            onClick={() => {
                                model.stop();
                                changePoints(() => []);
                                changeCurvePoints(() => []);
                            }}>Clear
                        </button>
                    </div>
                </div>
                <div className="regression-low-level__loss">
                    <LossPlot
                              loss={lossHistory}/>
                </div>

            </div>
        </div>
    )
}

Resultado:

Eu recomendo fazer as seguintes tarefas:

para implementar a aproximação da função pela função logarítmica
para o otimizador tf.train.sgd, tente brincar com learningRate e observe como o processo de aprendizagem muda. Tente definir o learningRate muito alto para obter a imagem mostrada na Figura 2.
defina o otimizador para tf.train.adam. O processo de aprendizagem melhorou? Se o processo de aprendizado depende da alteração do valor de learningRate no construtor do modelo.

TensorFlow.js: parte 1: usando a API de baixo nível para aproximar funções lineares