
No processo de desenvolvimento de um jogo em categorias de gênero completamente diferentes, pode ser necessário "lançar" qualquer objeto do jogo ao longo de uma curva suave a uma velocidade constante ou controlada, seja um caminhão movendo-se da cidade A para a cidade B, um míssil disparado ao longo de uma trajetória astuta ou um avião inimigo executar uma manobra deitada.
Provavelmente, todo mundo relacionado ao tópico conhece ou pelo menos ouviu falar sobre curvas de Bézier, B-splines, Hermite splines e outras interpolações e splines de suavização e sugeririam absolutamente corretamente o uso de uma delas na situação descrita, mas nem tudo é tão simples como gostaríamos.
No nosso caso, uma spline é uma função que exibe um conjunto de parâmetros de entrada (pontos de controle) e o valor de um argumento (geralmente assumindo valores de 0 a 1) para um ponto em um plano ou no espaço. A curva resultante é o conjunto de valores da função spline para...
Como exemplo, considere a curva de Bézier cúbica , que é dada pela seguinte equação:


Curva Cúbica de Bézier
A figura mostra duas curvas cúbicas de Bézier, definidas por quatro pontos (a curva passa por dois deles, os dois restantes definem a curvatura).
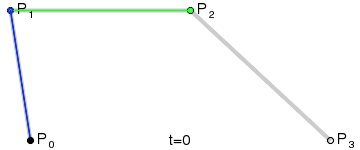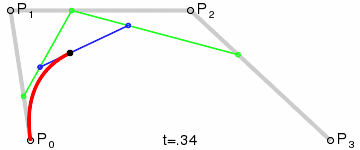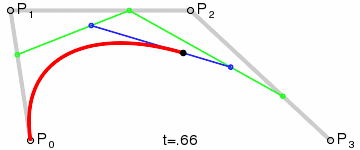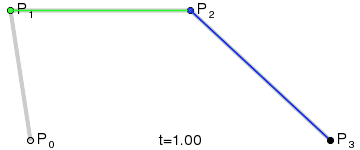
Animação de exibição do parâmetro t para um ponto de curva
A fim de construir uma rota mais complexa e variável a partir das seções da curva, elas podem ser conectadas em uma cadeia, deixando um elo de ponto comum:
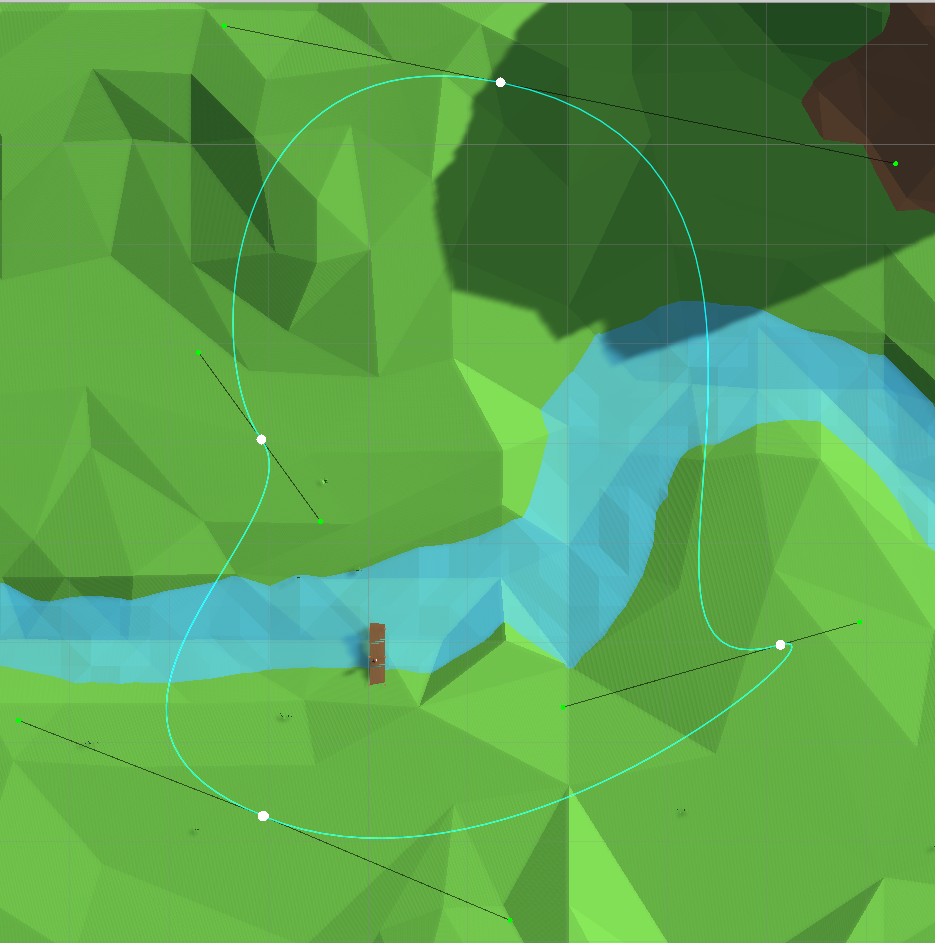
Spline por partes Nós
descobrimos a tarefa e parametrização da rota, agora voltamos à questão principal. Para que nosso plano condicional se mova ao longo da rota a uma velocidade constante, precisamos a qualquer momento ser capazes de calcular um ponto na curva, dependendo da distância percorrida ao longo dessa curva., embora tenha apenas a capacidade de calcular a posição de um ponto na curva a partir do valor do parâmetro (função ) É nesta fase que começam as dificuldades.
Meu primeiro pensamento foi fazer um mapeamento linear e calcular do valor resultante - fácil, computacionalmente barato, em geral, o que você precisa.

O problema com este método é imediatamente óbvio - na verdade, a distância percorrida depende de não linearmente, e para estarmos convencidos disso, basta organizar ao longo da rota uniformemente distribuída por valor pontos: pontos

"uniformemente" distribuídos ao longo do trajeto
A aeronave irá desacelerar em alguns trechos e acelerar em outros, o que torna este método de parametrização da curva completamente inaplicável para a solução do problema descrito (o avião foi escolhido exclusivamente como exemplo ilustrativo e o objetivo de descrever seu movimento de forma fisicamente correta não foi perseguido ):

Visualização da parametrização incorreta da curva
Após consultar o mecanismo de busca, no stackoverflow e no youtube , encontrei uma segunda forma de calcular, a saber, a representação da curva na forma de uma função linear por partes (calculando um conjunto de pontos equidistantes uns dos outros ao longo da curva):
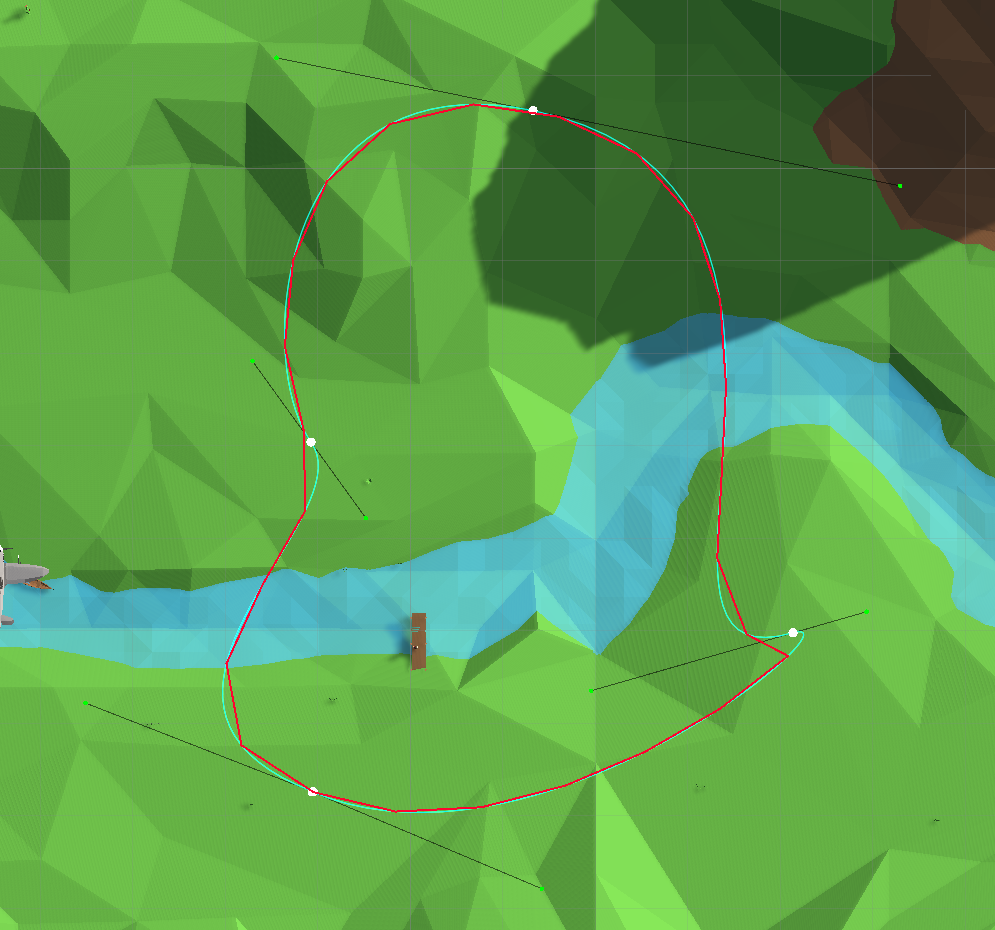
Representação da curva como uma spline linear por partes
Este procedimento é iterativo: um pequeno passo é dado, nós nos movemos ao longo de uma curva com ele, somando a distância percorrida como o comprimento de uma spline linear por partes até que uma determinada distância seja coberta, após o que o ponto é lembrado e o processo é retomado.
Código de amostra
Uma fonte
public Vector2[] CalculateEvenlySpacedPoints(float spacing, float resolution = 1)
{
List<Vector2> evenlySpacedPoints = new List<Vector2>();
evenlySpacedPoints.Add(points[0]);
Vector2 previousPoint = points[0];
float dstSinceLastEvenPoint = 0;
for (int segmentIndex = 0; segmentIndex < NumSegments; segmentIndex++)
{
Vector2[] p = GetPointsInSegment(segmentIndex);
float controlNetLength = Vector2.Distance(p[0], p[1]) + Vector2.Distance(p[1], p[2]) + Vector2.Distance(p[2], p[3]);
float estimatedCurveLength = Vector2.Distance(p[0], p[3]) + controlNetLength / 2f;
int divisions = Mathf.CeilToInt(estimatedCurveLength * resolution * 10);
float t = 0;
while (t <= 1)
{
t += 1f/divisions;
Vector2 pointOnCurve = Bezier.EvaluateCubic(p[0], p[1], p[2], p[3], t);
dstSinceLastEvenPoint += Vector2.Distance(previousPoint, pointOnCurve);
while (dstSinceLastEvenPoint >= spacing)
{
float overshootDst = dstSinceLastEvenPoint - spacing;
Vector2 newEvenlySpacedPoint = pointOnCurve + (previousPoint - pointOnCurve).normalized * overshootDst;
evenlySpacedPoints.Add(newEvenlySpacedPoint);
dstSinceLastEvenPoint = overshootDst;
previousPoint = newEvenlySpacedPoint;
}
previousPoint = pointOnCurve;
}
}
return evenlySpacedPoints.ToArray();
}E, ao que parece, o problema está resolvido, porque você pode dividir a rota em vários segmentos e desfrutar de como o objeto se move de maneira suave e constante, já que calcular um ponto em uma função linear por partes é uma questão simples e rápida. Mas essa abordagem também tem desvantagens bastante óbvias que me assombravam - um procedimento bastante caro para alterar a etapa de partição ou geometria da curva e a necessidade de encontrar um equilíbrio entre precisão (mais consumo de memória) e economia de memória (a rota "interrompida" se torna mais perceptível).
Como resultado, continuei procurando e encontrei um excelente artigo "Movendo-se ao longo de uma curva com velocidade especificada" , com base no qual se baseiam mais raciocínios.
O valor da velocidade pode ser calculado comoOnde - função spline. Para resolver o problema, você precisa encontrar a funçãoOnde - o comprimento do arco do ponto inicial ao desejado, e esta expressão estabelece a relação entre e ...
Usando a substituição de variável de diferenciação, podemos escrever
Levando em consideração que a velocidade é uma quantidade não negativa, obtemos
Porque pela condição de que o módulo do vetor de velocidade permanece inalterado (em geral, não é igual a um, mas a uma constante, mas para simplificar os cálculos, tomaremos essa constante igual a um).
Agora temos a proporção entre e explicitamente:
de onde o comprimento total da curva é obviamente calculado como ... Usando a fórmula resultante, é possível, tendo o valor do argumento, calcule o comprimento do arco até o ponto em que este valor é é exibido.
Estamos interessados na operação reversa, ou seja, calcular o valor do argumento ao longo de um determinado comprimento de arco :
Uma vez que não existe uma maneira analítica geral de encontrar a função inversa, você terá que procurar uma solução numérica. Nós denotamos Para um dado , é necessário encontrar esse valor em qual ... Assim, a tarefa se tornou a tarefa de encontrar a raiz da equação, com a qual o método de Newton pode lidar perfeitamente.
O método forma uma sequência de aproximações do formulário
Onde
Calcular precisa calcular , cujo cálculo, por sua vez, requer integração numérica.
Escolhacomo uma aproximação inicial agora parece razoável (lembre-se da primeira abordagem para resolver o problema).
Em seguida, iteramos usando o método de Newton até que o erro da solução se torne aceitável ou o número de iterações feitas seja proibitivamente grande.
Existe um problema potencial com o uso do método padrão de Newton. Função - não decrescente, pois sua derivada não é negativo. Se a segunda derivada, então a função é chamada de convexa e o método de Newton nela convergirá para a raiz. No entanto, em nosso caso, pode acabar sendo negativo, devido ao qual o método de Newton pode convergir fora do intervalo de definição ... O autor do artigo propõe o uso de uma modificação do método de Newton, que, se o resultado da próxima iteração pelo método de Newton não cair no intervalo atual que delimita a raiz, selecione o meio do intervalo ( método da dicotomia ). Independentemente do resultado do cálculo na iteração atual, o intervalo é reduzido, o que significa que o método converge para a raiz.
Resta escolher o método de integração numérica - usei as quadraturas do método de Gauss , pois ele fornece um resultado bastante preciso a baixo custo.
Código de função para calcular t (s)
public float ArcLength(float t) => Integrate(x => TangentMagnitude(x), 0, t);
private float Parameter(float length)
{
float t = 0 + length / ArcLength(1);
float lowerBound = 0f;
float upperBound = 1f;
for (int i = 0; i < 100; ++i)
{
float f = ArcLength(t) - length;
if (Mathf.Abs(f) < 0.01f)
break;
float derivative = TangentMagnitude(t);
float candidateT = t - f / derivative;
if (f > 0)
{
upperBound = t;
if (candidateT <= 0)
t = (upperBound + lowerBound) / 2;
else
t = candidateT;
}
else
{
lowerBound = t;
if (candidateT >= 1)
t = (upperBound + lowerBound) / 2;
else
t = candidateT;
}
}
return t;
}
Código de função de integração numérica
private static readonly (float, float)[] CubicQuadrature =
{(-0.7745966F, 0.5555556F), (0, 0.8888889F), (0.7745966F, 0.5555556F)};
public static float Integrate(Func<float, float> f, in float lowerBound, in float uppedBound)
{
var sum = 0f;
foreach (var (arg, weight) in CubicQuadrature)
{
var t = Mathf.Lerp(lowerBound, uppedBound, Mathf.InverseLerp(-1, 1, arg));
sum += weight * f(t);
}
return sum * (upperBound - lowerBound) / 2;
}A seguir, você pode ajustar o erro do método de Newton, escolher um método mais preciso de integração numérica, mas o problema, de fato, está resolvido - um algoritmo para calcular o argumento foi construído spline para um determinado comprimento de arco. Para combinar várias seções de curvas em uma e escrever um procedimento de cálculo generalizadovocê pode armazenar os comprimentos de todos os segmentos e pré-calcular o índice do segmento onde deseja realizar um procedimento iterativo usando o método de Newton modificado.
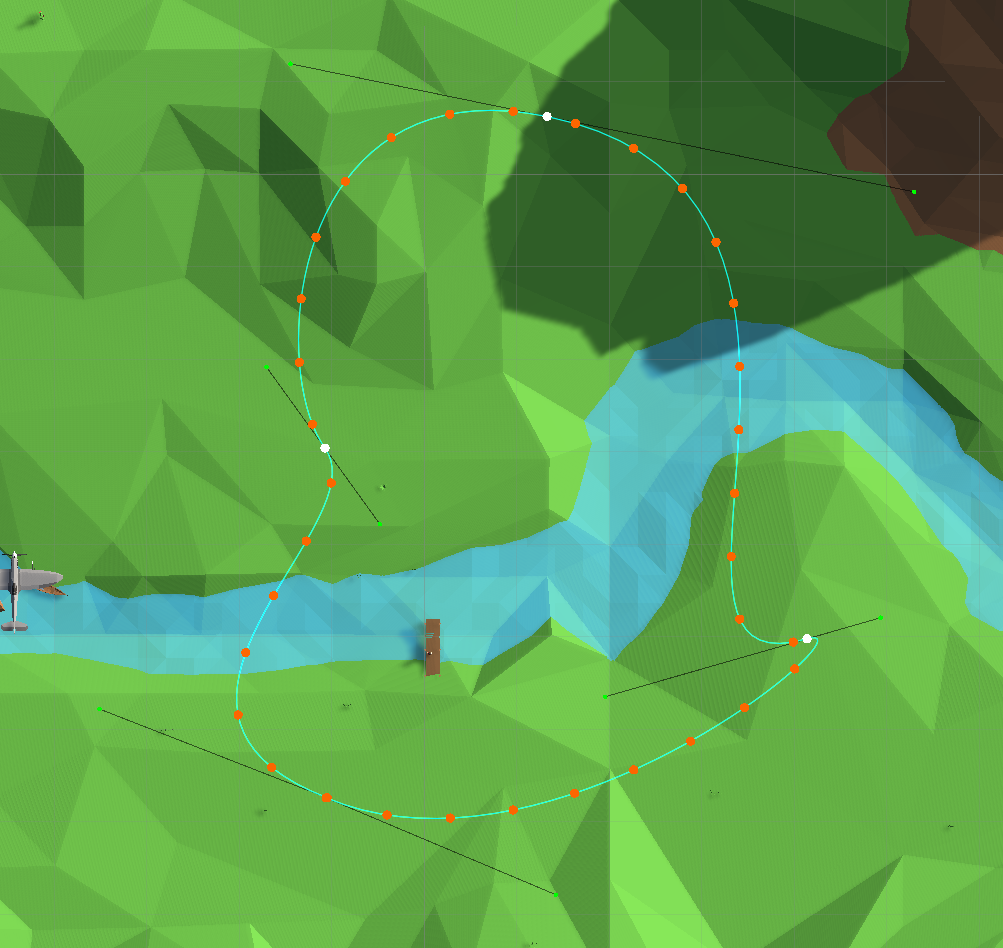
Pontos uniformemente distribuídos ao longo do caminho

Agora o plano se move uniformemente.
Assim, consideramos várias maneiras de parametrizar o spline em relação à distância percorrida, no artigo que usei como fonte, como opção, o autor sugere resolver numericamente a equação diferencial, mas, segundo sua própria observação, prefere o método modificado Newton:
Eu prefiro a abordagem do método de Newton porque geralmente t pode ser calculado mais rápido do que com solucionadores de equações diferenciais.
Como conclusão, darei uma tabela de tempo para calcular a posição de um ponto na curva mostrada nas capturas de tela em um thread em um processador i5-9600K:
| Número de cálculos | Tempo médio, ms |
|---|---|
| 100 | 0,62 |
| 1000 | 6,24 |
| 10.000 | 69,01 |
| 100.000 | 672,81 |