Olá, Habitantes! Um colosso com pés de barro é o que se pode chamar de um programador sem formação em Ciência da Computação. O domínio confiante do básico permite que você não “reinvente a roda” e crie soluções eficazes na arquitetura de software. Tudo isso elimina erros e custos excessivos de teste e refatoração.
Não importa se você se sente deslocado quando outros programadores estão discutindo o limite aproximado. Até mesmo especialistas experientes cometem erros porque se esqueceram da Ciência da Computação.
Por que este livro é necessário
Muitos dos meus colegas desenvolvedores (do autor) vieram para a profissão de uma ampla variedade de campos. Alguns têm educação superior em Ciência da Computação; outros estudaram fotografia, matemática ou nunca se formaram na universidade.
Nos últimos anos, percebi que os programadores estão cada vez mais ansiosos para aprender ciência da computação por uma série de razões:
- para se tornarem bons programadores;
- para responder a perguntas sobre algoritmos durante as entrevistas;
- para satisfazer sua curiosidade sobre a Ciência da Computação, ou finalmente para parar de lamentar que em algum momento não tiveram a oportunidade de dominar o assunto.
Este livro é para todos vocês.
Muitos encontrarão aqui tópicos que são interessantes por si próprios. Tentei mostrar em que situações reais (não acadêmicas) esse conhecimento será útil. Depois de ler este livro, quero que você adquira o mesmo conhecimento de depois de estudar o curso básico de Ciência da Computação e também aprenda a aplicá-lo.
Simplificando, o objetivo deste livro é ajudá-lo a se tornar um programador mais habilidoso e experiente por meio de um melhor entendimento da Ciência da Computação. Não posso espremer 20 anos de ensino universitário e experiência profissional em um livro ... mas vou tentar fazer o meu melhor. Espero que você encontre aqui pelo menos um tópico sobre o qual possa dizer: “Sim, agora entendo” - e aplicar o conhecimento no seu trabalho.
O que você não encontrará na edição
O significado do livro é ajudar o leitor a entender melhor a Ciência da Computação e aplicar o conhecimento na prática, e não substituir completamente quatro anos de estudo.
Em particular, este não é um livro de prova. De fato, no segundo volume do livro , métodos de prova são considerados, mas algoritmos padrão são geralmente apresentados aqui sem provas. A ideia é que o leitor conheça a existência desses algoritmos e saiba como utilizá-los sem entrar em detalhes. Como um livro de prova escrito para estudantes de graduação e pós-graduação, recomendo fortemente Introdução a Algoritmos de Cormen, Leiserson, Rivest e Stein (os autores são geralmente agrupados em abreviatura CLRS).
Este também não é um livro de programação: você não encontrará diretrizes sobre quando usar números do tipo int e quando usar double, ou uma explicação do que é um loop. Presume-se que o leitor será capaz de compreender as listagens de pseudocódigos usadas para descrever os algoritmos (todos os programas neste livro são escritos em pseudocódigos baseados na linguagem C). O objetivo do livro é conectar os conceitos da Ciência da Computação com técnicas de programação já familiares ao leitor.
10. Programação dinâmica
10.1. Problema de campos ausentes
Suponha que tenhamos um tabuleiro de xadrez n × n faltando vários quadrados. Como encontrar o maior pedaço de tabuleiro k × k sem campos ausentes?
Se você nunca enfrentou esse problema antes, reserve alguns minutos para escrever uma solução e determinar o tempo de execução do seu algoritmo.
Diante desse problema, raciocinei da seguinte maneira. Cada campo do tabuleiro de xadrez pode pertencer a muitas das maiores áreas, mas apenas em uma delas pode ser o canto superior esquerdo. Se eu marcar cada caixa com o tamanho da maior área intacta da qual é o canto superior esquerdo, então a caixa com a maior dessas marcas corresponderá à área desejada.
Suponha que o tabuleiro seja representado como uma matriz n × n em que cada célula contém 1 se o campo correspondente estiver presente e 0 se estiver ausente. Se o valor da célula atual for 0, o campo correspondente está ausente e não pode fazer parte de um segmento contíguo, portanto, não precisa ser alterado. Se o valor for 1, podemos substituí-lo por um número um a mais do que o valor mínimo das três células localizadas abaixo e à direita.
Mudamos cada célula da matriz uma vez, incluindo verificar se o valor da célula é zero, verificar os valores de até mais três células e escrever o novo valor da célula. Cada uma dessas operações leva O (1) tempo, então o tempo que leva para processar todo o tabuleiro é
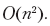
Observe que este é linear, não quadrático, o tempo de execução do algoritmo - em um tabuleiro de xadrez n (assumimos que n é o número total de campos e aderimos à convenção usual de que n é a quantidade de dados de entrada) campos (alguns deles são ausente), portanto o tempo total gasto pelo algoritmo é proporcional ao número de campos. Se denotarmos com mais precisão o tamanho do tabuleiro de xadrez como √ n × √ n, obteremos n campos e o tempo total de execução será O (n).
10,2. Trabalhar com subtarefas sobrepostas
A abordagem usada nesta seção é chamada de programação dinâmica. É usado quando um problema pode ser dividido em várias subtarefas, a solução de cada uma das quais será usada várias vezes. Essa abordagem difere do princípio de "dividir para conquistar", quando o problema é dividido em subtarefas, que são resolvidas de forma independente uma da outra. No problema do tabuleiro de xadrez, cada subproblema dependia das soluções para três outros problemas, e as soluções para todos os subproblemas eram salvas para uso posterior.
A programação dinâmica geralmente é feita pela construção de tabelas conforme mostrado acima. Isso significa resolver um problema usando uma abordagem de baixo para cima, onde começamos resolvendo os menores subproblemas e avançamos até chegarmos a uma resposta. Outro método é a memoização, onde vamos de cima para baixo, resolvendo subproblemas conforme necessário e armazenando os resultados em cache para reutilização. Construir tabelas é a opção preferida quando você precisa resolver cada subproblema (no meu exemplo com um tabuleiro de xadrez, foi necessário encontrar a maior área intacta para cada campo do tabuleiro), pois os custos deste método são menores do que com memoização. Se algumas subtarefas da área de solução não precisarem ser resolvidas, a memoização permitirá que você resolva apenas as subtarefas realmente necessárias.
O ponto-chave
Onde dividir e conquistar envolve dividir uma tarefa em várias subtarefas independentes, a programação dinâmica significa dividir uma tarefa em várias subtarefas sobrepostas. A solução para cada subproblema é armazenada em cache para reutilização posterior.
10,3. Programação dinâmica e caminhos mais curtos
Considere o problema de encontrar o caminho mais curto: para um determinado grafo com arestas ponderadas, você precisa encontrar um caminho de um nó para outro que tenha o menor custo.
Definição Um
gráfico com peso de aresta é um gráfico em que cada aresta tem seu próprio peso (custo). O custo de um caminho de um nó para outro é determinado pela soma do custo de todas as arestas cruzadas.
Suponha que encontramos um caminho entre os nós s e t que contém o terceiro nó v. Então, o caminho de s para t deve conter o caminho mais curto de s para v, porque, caso contrário, poderíamos substituir este segmento por um caminho mais curto e reduzir o comprimento do caminho mais curto de s para t, o que contradiz a condição inicial (este é o princípio de otimização de Bellman).
( ) , . , . , .
, , .
Os problemas de encontrar o caminho mais curto são exemplos notáveis de programação dinâmica, uma vez que a propriedade ótima de uma subestrutura é intuitivamente clara - é óbvio que o caminho mais rápido para ir do ponto A ao ponto C através do ponto B também é o caminho mais rápido para ir do ponto A ao ponto B e do ponto B ao ponto C. O número de algoritmos baseados neste princípio inclui o método Bellman - Ford, que encontra o caminho mais curto do ponto inicial a qualquer vértice do gráfico (ou de qualquer vértice do gráfico ao ponto final) e o método Floyd - Warshall - com sua ajuda o caminho mais curto entre cada par de vértices do gráfico é calculado. Em ambos os casos, a ideia é começar com um pequeno subconjunto de nós próximos aos nós de interesse e expandir gradativamente esse conjunto usando os nós já encontrados para calcular novas distâncias.
10.4.
10.4.1. Git merge
Outra tarefa comumente usada para demonstrar a programação dinâmica é encontrar a Subseqüência Comum Mais Longa. A tarefa é encontrar, para duas strings A e B, a sequência mais longa que ocorre em ambas as strings, mantendo a sequência de caracteres. As cordas não precisam estar em uma linha; por exemplo, se A = {acdbef} e B = {babdef}, então {adef} será sua subsequência comum.
Ao mesclar alterações no Git (mesclar), ele procura a maior subsequência comum para os ramos mestre e de trabalho. Os caracteres presentes no master, mas não presentes na maior subsequência comum, são removidos; caracteres que estão no ramo de trabalho, mas não estão nesta subsequência, são adicionados ao mestre.
10.4.2. LATEX
O sistema de preparação de documentos LATEX é freqüentemente usado para criar documentos técnicos. Uma das tarefas do sistema de digitação é alinhar o texto à direita e à esquerda ao mesmo tempo; para fazer isso, o espaçamento entre palavras e caracteres é aumentado ou reduzido para que todas as linhas tenham o mesmo comprimento. Outra maneira de alinhar o texto é quebrar a última palavra para que parte da palavra apareça na próxima linha. O LATEX (de um ponto de vista técnico, o sistema de entrada de texto TEX faz quase todo o trabalho; o LATEX é construído sobre o TEX. Aqui eu uso o LATEX por razões de simplicidade) tenta encontrar pontos de quebra de linha ideais para fazer o texto parecer bonito. Se isso falhar, várias linhas consecutivas terminarão com um hífen de palavra ou a distância entre as palavras em linhas diferentes será diferente.O LATEX possui um conjunto de regras para avaliar a "falha" do alinhamento. O programa busca encontrar a opção "menos ruim".
Se um parágrafo tiver n pontos de quebra de linha possíveis, haverá
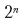opções possíveis para quebrar o texto. A “falha” da seleção para cada ponto de interrupção depende de quais pontos de interrupção foram selecionados antes dele. Portanto, temos subtarefas sobrepostas novamente. O uso de técnicas de programação dinâmica reduz o tempo de execução 
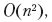que pode ser melhorado com métodos adicionais.
»Mais detalhes sobre o livro podem ser encontrados no site da editora
» Índice
» Trecho
Para Habitantes desconto de 25% no cupom - Ciência da Computação
Após o pagamento da versão em papel do livro, um e-book é enviado para o e-mail.