
Os problemas de segurança da informação requerem o estudo e a solução de uma série de problemas teóricos e práticos na interação de informações dos assinantes do sistema. Nossa doutrina de segurança da informação formula a tarefa tríplice de garantir a integridade, confidencialidade e disponibilidade das informações. Os artigos aqui apresentados são dedicados à consideração de questões específicas de sua solução no âmbito de vários sistemas e subsistemas de estado. Anteriormente, o autor considerou em 5 artigos as questões de garantir a confidencialidade das mensagens por meio de padrões estaduais. O conceito geral do sistema de codificação também foi fornecido por mim anteriormente .
Introdução
Pela minha educação básica, não sou um matemático, mas em relação às disciplinas que li na universidade, tive que entendê-la meticulosamente. Por muito tempo e persistentemente li os livros clássicos de nossas principais universidades, uma enciclopédia matemática de cinco volumes, muitas brochuras populares sobre questões específicas, mas não havia satisfação. A compreensão de leitura profunda também não surgiu.
Todos os clássicos matemáticos são focados, via de regra, no caso teórico infinito, e as disciplinas especiais são baseadas no caso de construções finitas e estruturas matemáticas. A diferença de abordagens é colossal, a ausência ou falta de bons exemplos completos é talvez a principal desvantagem e a falta de manuais universitários. Raramente há um livro de problemas com soluções para iniciantes (para calouros), e aqueles que existem são pecaminosos em omissões nas explicações. Em geral, apaixonei-me pelas livrarias técnicas de segunda mão, graças às quais a biblioteca e, em certa medida, o acervo de conhecimentos foram repostos. Tive oportunidade de ler muito, muito, mas "não fui".
Este caminho levou-me à questão: o que posso fazer sozinho sem livro "muletas", tendo à minha frente apenas uma folha de papel em branco e um lápis com borracha? Acabou sendo um pouco e não exatamente o que era necessário. O difícil caminho da autoeducação casual foi ultrapassado. A questão era esta. Posso construir e explicar, em primeiro lugar para mim mesmo, o trabalho de código que detecta e corrige erros, por exemplo, código de Hamming, (7, 4) -code?
Sabe-se que o código de Hamming é amplamente utilizado em muitas aplicações na área de armazenamento e troca de dados, especialmente em RAID; além disso, está na memória ECC e permite a correção instantânea de erros simples e duplos.
Segurança da informação. Códigos, cifras, mensagens steg
A interação de informações por meio da troca de mensagens entre seus participantes deve ser protegida em diferentes níveis e por diversos meios, tanto de hardware quanto de software. Essas ferramentas são desenvolvidas, projetadas e criadas dentro da estrutura de certas teorias (ver Figura A) e tecnologias adotadas por acordos internacionais sobre modelos OSI / ISO.
A proteção da informação em sistemas de telecomunicações da informação (STI) está se tornando praticamente o principal problema na solução de problemas de gestão, tanto na escala de um indivíduo - um usuário, quanto para empresas, associações, departamentos e o estado como um todo. De todos os aspectos da proteção ITKS, neste artigo consideraremos a proteção da informação durante sua extração, processamento, armazenamento e transmissão em sistemas de comunicação.
Esclarecendo ainda mais a área temática, enfocaremos duas direções possíveis nas quais duas abordagens diferentes para a proteção, apresentação e uso da informação são consideradas: sintática e semântica. A figura usa abreviações: codec - codec - decoder; shidesh - um decodificador-decodificador; guincho - corretivo - extrator.
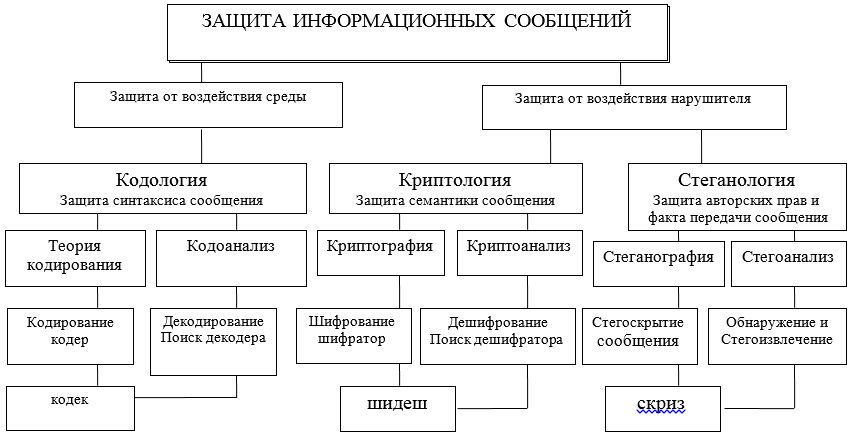
Figura A - Diagrama das principais direções e inter-relações das teorias destinadas a resolver os problemas de proteção da interação de informações
Os recursos sintáticos da apresentação de mensagens permitem controlar e garantir a correção e precisão (sem erros, integridade) da apresentação durante o armazenamento, processamento e, especialmente, ao transferir informações através dos canais de comunicação. Aqui, os principais problemas de proteção são resolvidos pelos métodos de codologia, sua grande parte - a teoria dos códigos de correção.
Segurança semântica (semântica)as mensagens são fornecidas por métodos de criptologia, que por meio da criptografia torna possível proteger um intruso potencial de dominar o conteúdo da informação. Nesse caso, o infrator pode copiar, roubar, alterar ou substituir, ou mesmo destruir a mensagem e seu portador, mas não poderá obter informações sobre o conteúdo e o significado da mensagem transmitida. O conteúdo das informações da mensagem permanecerá inacessível para o infrator. Assim, o assunto para consideração posterior será a proteção sintática e semântica da informação no ITCS. Neste artigo, nos restringiremos a considerar apenas a abordagem sintática em uma implementação simples, mas muito importante, corrigindo o código.
Vou traçar imediatamente uma linha divisória na solução de problemas de segurança da informação: a
teoria da codologiaprojetado para proteger informações (mensagens) de erros (proteção e análise da sintaxe das mensagens) do canal e ambiente, para detectar e corrigir erros;
a teoria da criptologia é projetada para proteger a informação do acesso não autorizado à sua semântica pelo intruso (proteção da semântica, o significado das mensagens);
a teoria da esteganologia visa proteger o fato da troca de informações de mensagens, bem como proteger os direitos autorais, os dados pessoais (proteção do sigilo médico).
Em geral, vamos. Por definição, e há alguns deles, nem é fácil entender que existe um código. Os autores escrevem que o código é um algoritmo, uma tela e algo mais. Não vou escrever sobre a classificação dos códigos aqui, direi apenas que o (7, 4) -código é bloco .
Em algum momento, percebi que o código são palavras de código especiais, um conjunto finito delas, que são substituídas por algoritmos especiais com o texto original da mensagem no lado de transmissão do canal de comunicação e que são enviadas através do canal para o destinatário. A substituição é realizada pelo dispositivo codificador e, no lado receptor, essas palavras são reconhecidas pelo dispositivo decodificador.
Uma vez que a função das partes é mutável, ambos os dispositivos são combinados em um e chamados de codec abreviado (codificador / decodificador) e são instalados em ambas as extremidades do canal. Além disso, como existem palavras, também existe um alfabeto. O alfabeto tem dois caracteres {0, 1}, bloco bináriocódigos. O alfabeto da língua natural (NL) é um conjunto de símbolos - letras que substituem os sons da fala oral durante a escrita. Aqui, não vamos nos aprofundar na escrita hieroglífica na escrita silábica ou nodular.
O alfabeto e as palavras já são uma linguagem, sabe-se que as línguas humanas naturais são redundantes, mas o que isso significa, onde habita a redundância da linguagem é difícil dizer, a redundância não é muito bem organizada, caótica. Ao codificar, armazenar informações, eles tendem a reduzir a redundância, por exemplo, arquivadores, código Morse, etc.
Richard Hemming provavelmente percebeu mais cedo do que outros que, se a redundância não for eliminada, mas razoavelmente organizada, ela pode ser usada em sistemas de comunicação para detectar erros e corrigi-los automaticamente nas palavras-código do texto transmitido. Ele percebeu que todas as 128 palavras binárias de 7 bits podem ser usadas para detectar erros em palavras-código que formam um código - um subconjunto de 16 palavras binárias de 7 bits. Foi um palpite brilhante.
Antes da invenção de Hamming, erros também eram detectados pelo lado receptor quando o texto decodificado não podia ser lido ou não era bem o que era necessário. Nesse caso, foi enviado um pedido ao remetente da mensagem para repetir os blocos de certas palavras, o que, claro, era muito inconveniente e tornava as sessões de comunicação mais lentas. Esse era um grande problema que não era resolvido há décadas.
Construção de um código de Hamming (7, 4)
Voltemos a Hamming. Palavras do código (7, 4) são formadas a partir de 7 bits j = , j = 0 (1) 15, 4 informações e 3 símbolos de verificação, ou seja, essencialmente redundantes, uma vez que não carregam nenhuma informação de mensagem. Foi possível representar esses três dígitos de verificação por funções lineares de 4 símbolos de informação em cada palavra, o que garantiu a detecção do fato de um erro e seu lugar nas palavras para fazer a correção. Um código (7, 4) ganhou um novo adjetivo e se tornou umbloco binário linear. Dependências funcionais lineares (regras (*)) para calcular os valores dos símbolos
são os seguintes:
Corrigir o erro tornou-se uma operação muito simples - um caractere (zero ou um) foi determinado no bit incorreto e substituído por outro oposto 0 por 1 ou 1 por 0. Quantas palavras diferentes formam o código? A resposta a esta pergunta para o código (7, 4) é muito simples. Uma vez que existem apenas 4 dígitos de informação, e sua variedade, quando preenchida com símbolos, tem
= 16 opções, então simplesmente não há outras possibilidades, ou seja, um código composto por apenas 16 palavras garante que essas 16 palavras representem toda a escrita de todo o idioma.
As partes informativas dessas 16 palavras são numeradas #
( ):
0 = 0000; 4 = 0100; 8 = 1000; 12 = 1100;
1 = 0001; 5 = 0101; 9 = 1001; 13 = 1101;
2 = 0010; 6 = 0110; 10 = 1010; 14 = 1110;
3 = 0011; 7 = 0111; 11 = 1011; 15 = 1111.
Cada uma dessas palavras de 4 bits precisa ser calculada e adicionada à direita por 3 bits de verificação, que são calculados de acordo com as regras (*). Por exemplo, para a palavra de informação nº 6 igual a 0110, temos e os cálculos dos símbolos de verificação fornecem o seguinte resultado para esta palavra:
A sexta palavra-código neste caso assume a forma:
Da mesma forma, é necessário calcular os símbolos de verificação para todas as 16 palavras-código. Vamos preparar uma tabela K de 16 linhas para as palavras-código e preencher sequencialmente suas células (recomendo ao leitor que faça isso com um lápis na mão).
Tabela K - palavras-código j, j = 0 (1) 15, (7, 4) - códigos de Hamming
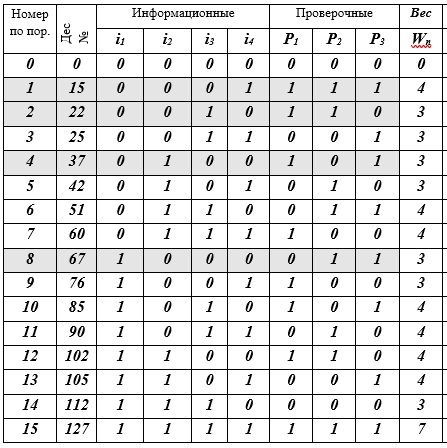
Descrição da tabela: 16 linhas - palavras de código; 10 colunas: número de sequência, representação decimal da palavra-código, 4 símbolos de informação, 3 símbolos de verificação, peso W da palavra-código é igual ao número de bits diferentes de zero (≠ 0). 4 palavras de código-linhas são destacadas por preenchimento - esta é a base do subespaço vetorial. Na verdade, isso é tudo - o código é construído.
Assim, a tabela contém todas as palavras (7, 4) - o código de Hamming. Como você pode ver, não foi muito difícil. A seguir, falaremos sobre quais ideias levaram Hamming a essa construção de código. Estamos todos familiarizados com o código Morse, com o alfabeto do semáforo naval e outros sistemas construídos em diferentes princípios heurísticos, mas aqui no código (7, 4), princípios e métodos matemáticos rigorosos são usados pela primeira vez. A história será apenas sobre eles.
Fundamentos matemáticos do código. Álgebra superior
Chegou a hora de contar como R. Hemming teve a ideia de abrir esse código. Não tinha ilusões especiais sobre seu talento e modestamente formulou uma tarefa para si: criar um código que detectasse e corrigisse um erro em cada palavra (na verdade, até dois erros foram detectados, mas apenas um deles foi corrigido). Com canais de qualidade, mesmo um erro é um evento raro. Portanto, o plano de Hemming ainda era grandioso na escala do sistema de comunicações. Houve uma revolução na teoria da codificação após sua publicação.
Era 1950. Estou dando aqui minha descrição simples (espero, compreensível), que não vi de outros autores, mas como descobri, nem tudo é tão simples. Demorou conhecimento de várias áreas da matemática e tempo para compreender profundamente tudo e entender por si mesmo porque isso é feito dessa maneira. Só depois disso pude apreciar a ideia bonita e bastante simples que é implementada neste código de correção. Passei a maior parte do tempo lidando com a técnica de cálculos e a justificativa teórica de todas as ações sobre as quais estou escrevendo aqui.
Os criadores dos códigos, por muito tempo, não conseguiram pensar em um código que detectasse e corrigisse dois erros. As ideias usadas por Hemming não funcionaram lá. Tive de procurar e novas ideias foram encontradas. Muito interessante! Cativa. Demorou cerca de 10 anos para encontrar novas ideias e só depois disso houve um avanço. Os códigos que mostram um número arbitrário de erros foram recebidos com relativa rapidez.
Espaços vetoriais, campos e grupos . O código (7, 4) resultante (Tabela K) representa um conjunto de palavras-código que são elementos de um subespaço vetorial (de ordem 16, com dimensão 4), ou seja, parte de um espaço vetorial de dimensão 7 com ordemDas 128 palavras, apenas 16 estão incluídas no código, mas foram incluídas no código por um motivo.
Primeiro, eles são um subespaço com todas as propriedades e singularidades resultantes; em segundo lugar, as palavras-código são um subgrupo de um grande grupo de ordem 128, além disso, um subgrupo aditivo de um campo de Galois estendido finito GF () grau de expansão n = 7 e característica 2. Este grande subgrupo é decomposto em classes adjacentes por um subgrupo menor, que é bem ilustrado pela seguinte tabela D. A tabela é dividida em duas partes: superior e inferior, mas deve ser lida como uma longa. Cada classe adjacente (linha da tabela) é um elemento do grupo de fatores pela equivalência de componentes.
Tabela D - Decomposição do grupo aditivo do campo Galois GF () em cosets (linhas da Tabela D) para o subgrupo de 16ª ordem.
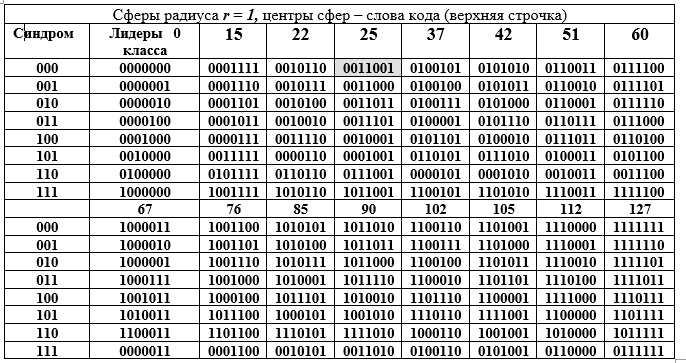
As colunas da tabela são esferas de raio 1. A coluna da esquerda (repetida) é a síndrome da palavra (7, 4) código de Hamming, a próxima coluna são os líderes da classe contígua. Vamos abrir a representação binária de um dos elementos (o 25º é destacado por preenchimento) do grupo de fatores e sua representação decimal:
Técnica de obtenção de linhas da tabela D. Um elemento da coluna de líderes de uma classe é somado com cada elemento do cabeçalho de uma coluna da tabela D (a soma é realizada para a linha do líder na forma binária mod2). Como todos os líderes de classe têm peso W = 1, todas as somas diferem da palavra no cabeçalho da coluna em apenas uma posição (a mesma para a linha inteira, mas diferente para a coluna). A Tabela D tem uma interpretação geométrica maravilhosa. Todas as 16 palavras-código são representadas pelos centros das esferas no espaço vetorial de 7 dimensões. Todas as palavras da coluna diferem da palavra superior na mesma posição, ou seja, estão na superfície de uma esfera com raio r = 1.
Essa interpretação esconde a ideia de detectar um erro em qualquer palavra de código. Trabalhamos com esferas. A primeira condição para detecção de erro é que as esferas de raio 1 não se toquem ou se cruzem. Isso significa que os centros das esferas estão a uma distância de 3 ou mais entre si. Nesse caso, as esferas não apenas não se cruzam, mas também não se tocam. Este é um requisito para a clareza da decisão: que esfera deve ser atribuída à palavra errada recebida no lado receptor pelo decodificador (não um código de 128 -16 = 112).
Em segundo lugar, todo o conjunto de palavras binárias de 7 bits de 128 palavras é distribuído uniformemente em 16 esferas. O decodificador só pode obter uma palavra desse conjunto de 128 palavras conhecidas com ou sem erro. Terceiro, o lado receptor pode receber uma palavra sem erro ou com distorção, mas sempre pertencendo a uma das 16 esferas, o que é facilmente determinado pelo decodificador. Na última situação, é tomada a decisão de que uma palavra de código foi enviada - o centro de uma esfera determinado pelo decodificador, que encontrou a posição (interseção de uma linha e uma coluna) da palavra na tabela D, ou seja, os números da coluna e da linha.
Aqui surge um requisito para as palavras do código e para o código como um todo: a distância entre quaisquer duas palavras-código deve ser de pelo menos três, ou seja, a diferença para um par de palavras-código, por exemplo, i = 85 == 1010101; j = 25 == 0011001 deve ser pelo menos 3; 85 - 25 = 1010101 - 0011001 = 1001100 = 76, o peso da palavra de diferença W (76) = 3. (A Tabela D substitui o cálculo de diferenças e somas). Aqui, a distância entre vetores de palavras binárias é entendida como o número de posições não correspondentes em duas palavras. Trata-se da distância de Hamming, que se tornou amplamente utilizada na teoria e na prática, pois satisfaz todos os axiomas da distância.
Observação . O código (7, 4) não é apenas um código binário de bloco linear , mas também um código de grupo , ou seja, as palavras do código formam um grupo algébrico por adição. Isso significa que quaisquer duas palavras-código, quando somadas, fornecem novamente uma das palavras-código. Só que esta não é uma operação de adição comum, é a adição do módulo dois.
Tabela E - A soma dos elementos do grupo (palavras-código) usados para construir o código de Hamming
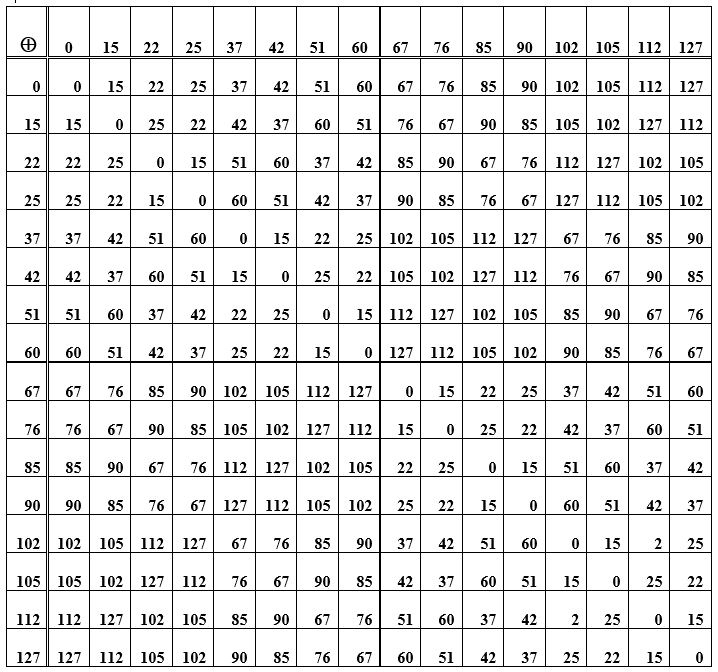
A operação de somar palavras em si é associativa, e para cada elemento no conjunto de palavras-código há um oposto a ele, ou seja, somar a palavra original com o oposto dá valor zero. Essa palavra-código zero é o elemento neutro do grupo. Na tabela D, esta é a diagonal principal dos zeros. O resto das células (intersecções de linha / coluna) são representações de números decimais de palavras de código obtidas pela soma de elementos de uma linha e uma coluna. Quando você reorganiza as palavras em lugares (ao somar), o resultado permanece o mesmo, além disso, a subtração e a adição de palavras têm o mesmo resultado. Além disso, um sistema de codificação / decodificação que implementa o princípio sindrômico é considerado.
Aplicação de código. Coder
O codificador está localizado no lado de transmissão do canal e é usado pelo remetente da mensagem. O remetente da mensagem (o autor) forma a mensagem no alfabeto da linguagem natural e a apresenta em formato digital. (O nome do caractere em código ASCII e em binário).
É conveniente gerar textos em arquivos para um PC usando um teclado padrão (códigos ASCII). Cada caractere (letra do alfabeto) corresponde a um octeto de bits (oito bits) nesta codificação. Para o (7, 4) - código de Hamming, em cujas palavras existem apenas 4 símbolos de informação, ao codificar um símbolo de teclado em uma letra, são necessárias duas palavras de código, ou seja, um octeto de uma letra é dividido em duas palavras de informação da linguagem natural (NL) do formulário
...
Exemplo 1 . É necessário transferir a palavra "dígito" em NL. Entramos na tabela de códigos ASCII, as letras correspondem a: c –11110110 e –11101000, f - 11110100, p - 11110000 e - 11100000 octetos. Ou então, em códigos ASCII, a palavra "dígito" = 1111 0110 1110 1000 1111 0100 1111 0000 1110 0000
com uma divisão em tétrades (4 dígitos cada). Assim, a codificação da palavra "dígito" NL requer 10 palavras de código do código de Hamming (7, 4). Os tétrades representam os bits informativos das palavras da mensagem. Essas palavras de informação (tétrades) são convertidas em palavras de código (7 bits cada) antes de serem enviadas ao canal da rede de comunicação. Isso é feito por multiplicação de matriz vetorial: a palavra de informação pela matriz geradora. O pagamento por conveniência é muito caro e demorado, mas tudo funciona de forma automática e, o mais importante, a mensagem fica protegida de erros.
A matriz geradora do código de Hamming (7, 4) ou o gerador de palavras-código é obtida escrevendo os vetores básicos do código e combinando-os em uma matriz. Isso segue do teorema da álgebra linear: qualquer vetor de um espaço (subespaço) é uma combinação linear de vetores de base, ou seja, linearmente independente neste espaço. Isso é exatamente o que é necessário - gerar quaisquer vetores (palavras-código de 7 bits) a partir dos de 4 bits de informação.
A matriz geradora do código de Hamming (7, 4, 3) ou o gerador de palavras de código tem a forma:
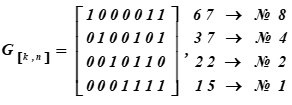
À direita estão as representações decimais das palavras de código da Base do subespaço e seus números de série na tabela K
No. i linhas da matriz são as palavras do código que são a base do subespaço vetorial.
Um exemplo de codificação de palavras de mensagens de informação (a matriz geradora do código é construída a partir dos vetores básicos e corresponde à parte da tabela K). Na tabela de códigos ASCII, usamos a letra q = <1111 0110>.
As palavras informativas da mensagem são semelhantes a:
...
São metade do caractere (c). Para o código (7, 4) definido anteriormente, é necessário encontrar as palavras-código correspondentes à palavra-mensagem de informação (c) de 8 caracteres na forma:
...
Para transformar esta carta-mensagem (q) em palavras-código u, cada metade da letra-mensagem i é multiplicada pela matriz geradora G [k, n] do código (matriz para a tabela K):
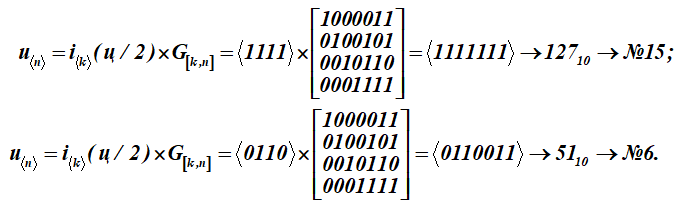
Temos duas palavras-código com números de série 15 e 6.
Mostrar formação detalhada do resultado inferior # 6 - uma palavra de código (multiplicação de uma linha de uma palavra de informação pelas colunas de uma matriz geradora); somatório sobre (mod2)
<0110> ∙ <1000> = 0 ∙ 1 + 1 ∙ 0 + 1 ∙ 0 + 0 ∙ 0 = 0 (mod2);
<0110> ∙ <0100> = 0 ∙ 0 + 1 ∙ 1 + 1 ∙ 0 + 0 ∙ 0 = 1 (mod2);
<0110> ∙ <0010> = 0 ∙ 0 + 1 ∙ 0 + 1 ∙ 1 + 0 ∙ 0 = 1 (mod2);
<0110> ∙ <0001> = 0 ∙ 0 + 1 ∙ 0 + 1 ∙ 0 + 0 ∙ 1 = 0 (mod2);
<0110> ∙ <0111> = 0 ∙ 0 + 1 ∙ 1 + 1 ∙ 1 + 0 ∙ 1 = 0 (mod2);
<0110> ∙ <1011>= 0 ∙ 1 + 1 ∙ 0 + 1 ∙ 1 + 0 ∙ 1 = 1 (mod2);
<0110> ∙ <1101> = 0 ∙ 1 + 1 ∙ 1 + 1 ∙ 0 + 0 ∙ 1 = 1 (mod2).
Recebido como resultado da multiplicação, a décima quinta e a sexta palavras da Tabela K. Os primeiros quatro bits nessas palavras de código (resultados da multiplicação) representam palavras de informação. Eles parecem:, (na tabela ASCII é apenas metade da letra t). Para a matriz de codificação, o conjunto de palavras com os números: 1, 2, 4, 8 são selecionados como vetores base na tabela K. Na tabela eles são destacados por preenchimento. Então, para esta tabela K, a matriz de codificação receberá a forma G [k, n].
Como resultado da multiplicação, 15 e 6 palavras da tabela de códigos K foram obtidas.
Aplicação de código. Decodificador
O decodificador está localizado no lado receptor do canal onde está o receptor da mensagem. O objetivo do decodificador é fornecer ao destinatário a mensagem transmitida na forma em que ela existia no remetente no momento do envio, ou seja, o destinatário pode usar o texto e as informações dele para seus trabalhos futuros.
A principal tarefa do decodificador é verificar se a palavra recebida (7 bits) é a que foi enviada no lado transmissor, se a palavra contém erros. Para resolver este problema, para cada palavra recebida pelo decodificador, multiplicando-a pela matriz de verificação H [nk, n], uma síndrome de vetor curto S (3 bits) é calculada.
Para palavras que são código, ou seja, não contêm erros, a síndrome sempre assume valor zero S = <000>. Para uma palavra com erro, a síndrome não é zero S ≠ 0. O valor da síndrome permite detectar e localizar a posição do erro até um bit na palavra recebida no lado receptor, e o decodificador pode alterar o valor desse bit. Na matriz de verificação do código, o decodificador encontra uma coluna que coincide com o valor da síndrome, e o número ordinal dessa coluna é igual ao bit corrompido pelo erro. Depois disso, para os códigos binários, o decodificador altera esse bit - basta substituí-lo pelo valor oposto, ou seja, um é substituído por zero e zero é substituído por um.
O código em questão é sistemático, isto é, os símbolos da palavra de informação são colocados em uma linha nos bits mais significativos da palavra de código. A recuperação de palavras de informação é realizada pelo simples descarte dos bits menos significativos (verificação), cujo número é conhecido. Além disso, uma tabela de códigos ASCII é usada na ordem inversa: a entrada são sequências binárias informativas e a saída são as letras do alfabeto da linguagem natural. Assim, o (7, 4) -código é sistemático, de grupo, linear, de bloco, binário .
A base do decodificador é formada pela matriz de verificação Í [nk, n], que contém o número de linhas igual ao número de símbolos de verificação, e todas as colunas possíveis, exceto zero, colunas de três caracteres... A matriz de verificação de paridade é construída a partir das palavras da tabela K, elas são escolhidas de modo a serem ortogonais à matriz de codificação, ou seja, seu produto é a matriz zero. A matriz de verificação assume a seguinte forma nas operações de multiplicação, ela é transposta. Para um exemplo específico, a matriz de verificação H [nk, n] é fornecida abaixo:
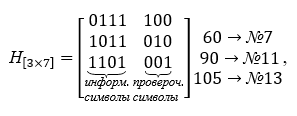



Vemos que o produto da matriz geradora e da matriz de verificação resulta em uma matriz zero.
Exemplo 2. Decodificando uma palavra do código de Hamming sem erro (e <7> = <0000000>).
Deixe na extremidade receptora do canal as palavras recebidas # 7 → 60 e # 13 → 105 da tabela K,
u <7> + e <7> = <0 1 1 1 1 0 0> + <0 0 0 0 0 0 0>,
onde não há erro, ou seja, tem a forma e <7> = <0 0 0 0 0 0 0>.

Como resultado, a síndrome calculada tem valor zero, o que confirma a ausência de erro nas palavras do código.
Exemplo 3 . Detecção de um erro em uma palavra recebida na extremidade receptora do canal (Tabela K).
A) Que seja necessário transmitir a 7ª palavra-código, ou seja,
u <7> = <0 1 1 1 1 0 0> e em um terço da esquerda da palavra, um erro foi cometido. Em seguida, é somado o mod2 com a 7ª palavra de código transmitida pelo canal de comunicação
u <7> + <7> = <0 1 1 1 1 0 0> + <0 0 1 0 0 0 0> = <0 1 0 1 1 0 0>,
onde o erro tem a forma e <7> = <0 0 1 0 0 0 0>.
O estabelecimento do fato de distorção da palavra-código é realizado multiplicando-se a palavra distorcida recebida pela matriz de verificação do código. O resultado desta multiplicação será um vetorchamada de síndrome da palavra-código.
Vamos realizar essa multiplicação para nossos dados originais (7º vetor com erro).

Como resultado dessa multiplicação, na extremidade receptora do canal, foi obtida uma síndrome vetorial S <nk>, cuja dimensão é (n - k). Se a síndrome S <3> = <0,0,0> for zero, conclui-se que a palavra recebida no lado receptor pertence ao código C e é transmitida sem distorção. Se a síndrome não for igual a zero S <3> ≠ <0,0,0>, então seu valor indica a presença de um erro e seu lugar na palavra. O bit distorcido corresponde ao número da posição da coluna da matriz [nk, n], que coincide com a síndrome. Depois disso, o bit distorcido é corrigido e a palavra recebida é processada posteriormente pelo decodificador. Na prática, uma síndrome é calculada imediatamente para cada palavra aceita e, se houver um erro, ela é automaticamente eliminada.
Portanto, durante os cálculos, a síndrome S = <110> é a mesma para as duas palavras. Olhamos a matriz de verificação e encontramos a coluna que corresponde à síndrome. Esta é a terceira coluna da esquerda. Portanto, o erro foi cometido no terceiro dígito da esquerda, que coincide com as condições do exemplo. Este terceiro bit é alterado para o valor oposto e retornamos as palavras recebidas pelo decodificador para a forma de código. O erro foi encontrado e corrigido.
Isso é tudo, é assim que o código clássico (7, 4) de Hamming funciona e funciona.
Inúmeras modificações e atualizações deste código não são consideradas aqui, uma vez que não são elas que são importantes, mas aquelas idéias e suas implementações que mudaram radicalmente a teoria da codificação e, como resultado, os sistemas de comunicação, troca de informações, sistemas de controle automatizados.
Conclusão
O artigo considera as principais disposições e tarefas da segurança da informação, nomeia as teorias destinadas a resolver esses problemas.
A tarefa de proteger a interação de informações de sujeitos e objetos de erros ambientais e das ações do infrator pertence à codologia.
O código de Hamming (7, 4) é considerado em detalhes, o que lançou as bases para uma nova direção na teoria da codificação - a síntese dos códigos de correção.
A aplicação de métodos matemáticos rigorosos usados na síntese de código é mostrada.
Exemplos são dados para ilustrar a eficiência do código.
Literatura
Peterson W., Weldon E. Códigos de correção de erros: Trans. do inglês. M.: Mir, 1976, 594 p.
Bleihut R. Teoria e prática de códigos de controle de erros. Traduzido do inglês. M.: Mir, 1986, 576 p.