🚓 👨🏾‍💼 🚐 Construção da curva de desconto. Programa educacional para um geek, parte 5 ↩️ 🍐 💈

Vamos aprender como construir uma curva de desconto. Já vou dizer: é muito importante ter dados de mercado relevantes. Se você estiver procurando por swaps de taxas de juros para dólar, euro ou alguma outra moeda, não há muitas informações abertas na Internet. A maioria dos dados está disponível por meio de terminais de negociação ou de empresas especiais - provedores de dados de mercado. Encontrei dados sobre as coroas dinamarquesas, suecas e norueguesas, bem como dados para o euro e o dólar no site de um grande grupo bancário escandinavo.

A seguir, tentaremos traçar uma curva de desconto para a coroa sueca.

Este post é uma versão adaptada da minha terceira aula de vídeo " Construindo a Curva de Desconto " como parte do curso Finmath for Fintech.

Portanto, nossa curva de desconto para a coroa será as taxas noturnas para cada dia. A primeira coisa que sabemos é a chamada taxa básica - a taxa sobre depósitos curtos (empréstimos). Além disso, existem trocas conhecidas que variam de um ano a trinta anos. Para ilustrar o método, traçaremos uma curva de até dez anos. Os valores atuais dos dados de mercado podem ser vistos nesta imagem:

Para começar a traçar a curva, precisamos fazer algumas suposições.

Vamos supor, por uma questão de simplicidade, que nossos swaps são fixos swaps flutuantes com uma periodicidade de pagamentos a cada seis meses. Abaixo está o diagrama para uma troca de um ano. Sabemos que no início a taxa básica é zero por cento. Para calcular um preço de swap justo, precisamos saber o valor do fator de desconto de seis meses e do fator de desconto de 12 meses. O que teremos como "perna" flutuante? Suponha que iremos pagar o valor médio noturno para cada uma das faixas. Ou seja, o valor da "perna" flutuante em até seis meses - este será o valor médio noturno ao longo de 180 dias. A perna flutuante para o ponto de 12 meses será a mesma, só que aqui haverá uma soma do dia 181 ao dia 360.

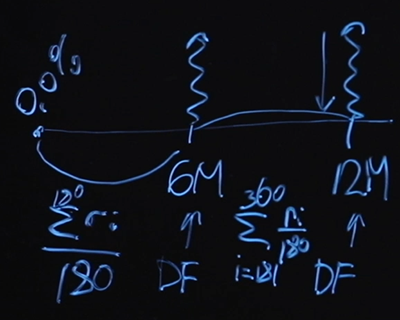
Este método de média é amplamente conhecido. É chamado de swap de índice noturno e é frequentemente usado em produtos de mercado. A perna flutuante é aqui definida como a média do período.

Conhecemos a taxa básica e o custo do swap. Obviamente, se escrevermos a fórmula para um preço justo "de frente", teremos muitas incógnitas. Não sabemos o fator de desconto para 6 meses, o fator de desconto para 12 meses, e não sabemos os valores das taxas de juros, exceto para um - o primeiro. Muitas incógnitas e apenas uma equação.

A seguinte hipótese nos ajudará a resolver esse problema. Conhecemos a taxa de juros no ponto zero - esta é a taxa básica. Assumiremos que nossas taxas de juros estão mudando linearmente. Vamos designar como X o valor da taxa de juros no ponto de 12 meses.

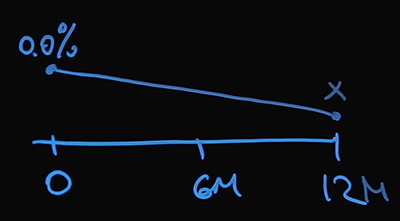
Aos 6 meses, será X / 2 (a média aritmética entre zero e X), e podemos encontrar o valor da taxa de juros em qualquer dia arbitrário. E não há nada difícil em calcular nossa taxa de juros flutuante nos pontos 6 e 12 meses:

\begin{array}{rcl} L_{1} & = & \frac{X}{4} \end{array}

$\begin{eqnarray} L_1&=& \frac{X}{4} \end{eqnarray}$

\begin{array}{rcl} L_{1} & = & \frac{3 X}{4} \end{array}

$\begin{eqnarray} L_1&=& \frac{3X}{4} \end{eqnarray}$

Agora, vamos passar para os fatores de desconto. Usamos uma curva de desconto com base na taxa overnight. Portanto, o fator de desconto no ponto seis meses é o produto de 180 fatores de desconto em cada ponto, e isso obviamente será algum tipo de função de X. O

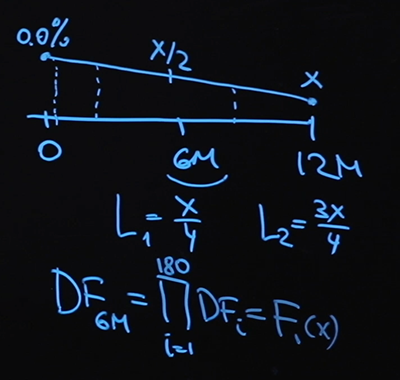
fator de desconto no ponto 12 meses é construído de forma semelhante com a única diferença de que preciso mais multiplicadores. Essa também será alguma função de X.

Assim, os fatores de desconto são expressos em termos de X, há também o primeiro e o segundo valores da taxa flutuante. Vamos continuar escrevendo a equação. Sabemos o valor do preço de swap, digamos que seja igual a P. Lembre-se da equação do preço justo. Precisamos multiplicar P pelo fator de desconto no ponto de doze meses e igualar à seguinte soma:

Deixe-me lembrar que o fator de desconto para um dia será determinado pela seguinte fórmula:

\begin{array}{rcl} D F_{i} & = & \frac{1}{(1 + \frac{r_{i}}{360})} \end{array}

$\begin{eqnarray} DF_i&=& \frac{1}{(1+\frac{r_i}{360})} \end{eqnarray}$

onde r _i é o valor da taxa de juros. Eu uso o número 360 supondo que há 360 dias em um ano (esta é uma convenção muito comum para calendários). Em qualquer ponto, sabemos como expressar o fator de desconto, r _i expresso em termos de X, usando interpolação linear. Nossa equação acabou com apenas uma incógnita e pode ser resolvida usando métodos numéricos. Como fazer isso - consulte o código Python .

Portanto, sabemos como encontrar o valor da nossa taxa no ponto 1 ano. Usando a suposição de interpolação linear e com base no valor de swap que conhecemos do mercado, encontraremos nosso valor para X. Aqui, plotamos a primeira seção de nossa curva:

Agora, para calcular o preço do swap para dois anos, precisamos do valor no ponto 6 meses, 12 meses, 18 meses e 2 anos. Usaremos exatamente a mesma suposição da última vez. Vamos chamar o valor da taxa desejada de Y e também usar a suposição sobre a linha de interpolação, restaurando a segunda seção da curva. Assim, passo a passo, chegaremos ao fim - ao ponto de 10 anos.

Este método é denominado bootstrap . Não é perfeito ou o único correto, mas é simples o suficiente para implementar e entender - o método bootstrap é ótimo como um nível inicial.

Encontramos a curva de desconto. O que isso nos dá? Falando formalmente, esses são os valores da taxa overnight em qualquer momento no futuro até dez anos. Você provavelmente pergunta: "Quem precisa disso?" Na verdade, é difícil imaginar um cenário em que um cliente venha até você e diga: "Quero abrir um depósito de um dia, que começará em 567 dias." Esta é uma situação um tanto incompreensível, e não se deve perceber a curva construída de forma tão direta.

Vamos imaginar que temos algum tipo de pagamento no futuro, digamos sete anos e meio. Pergunta: como sabemos seu valor atual?

Essa é exatamente a pergunta que a curva de desconto responderá. Iremos percorrer cada ponto da curva, calcular o fator de desconto em cada ponto e terminar nossa jornada no ponto por sete anos e meio, encontrar o fator de desconto resultante, multiplicar pelo pagamento - este será um preço justo.

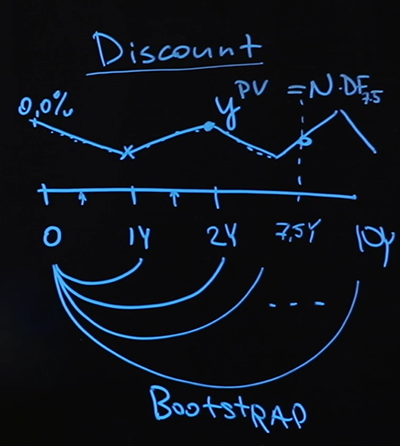
O modelo que usei, ou seja, quais taxas flutuantes tomei, como interpolei valores intermediários e, em geral, o fato de eu ter escolhido a interpolação foi muito determinado pelo tipo de dados que tenho. Eu tinha muito poucos dados - apenas uma taxa básica e valores de swap. Se houver mais dados disponíveis para mim, ou se forem diferentes, então provavelmente mudarei o modelo. Mas o método bootstrap (quando você plota a curva primeiro em uma seção curta, e depois plota mais e mais, dependendo dos valores obtidos anteriormente) ainda se aplica.

Agora lembre-se que além das curvas de desconto, precisamos das curvas LIBOR (TIBOR, EURIBOR, etc.). A diferença estará em quais ferramentas adicionaremos ao nosso modelo de cálculo. Buscaremos contratos contendo LIBOR e de forma semelhante, utilizando o método bootstrap, reconstruiremos a curva LIBOR.

Se você tiver que construir uma curva LIBOR real, tenha muito cuidado com as ferramentas que usar para construí-la, avalie cuidadosamente o modelo que irá usar. Nesse caso, usei o desconto noturno, mas um método diferente é necessário para construir a curva LIBOR. Provavelmente, o desconto será a cada três ou seis meses, dependendo do instrumento. Se você tiver dados suficientes, pode plotar uma curva LIBOR, curva EURIBOR, curva TIBOR e qualquer outra.

Se um cliente vier até você com as palavras: “Quero um swap de taxa de juros não por dez anos, mas por 134 meses, em que pagarei a LIBOR flutuante a cada 25 dias”, isso não é um problema. Temos uma curva LIBOR, usamos a suposição de interpolação, podemos restaurar o valor LIBOR em qualquer ponto. Sabemos o valor da curva de desconto em cada ponto, também podemos calcular todos os pagamentos e encontrar o próprio preço da "perna" fixa que equilibra esses pagamentos flutuantes. Assim, você pode encontrar os valores de preços justos para absolutamente qualquer instrumento traçando várias curvas.

Então, vamos examinar os destaques novamente. Peguei os dados disponíveis e formulei algumas suposições. Primeiro, o cronograma de pagamento: com que freqüência, com que freqüência, cada parte paga uma perna fixa e uma perna flutuante. Em segundo lugar, como vou calcular a aposta na perna flutuante? A terceira suposição é sobre interpolação de aposta linear. Usando todas essas três suposições, formulei várias equações não lineares, que resolvi numericamente. O caderno Jupyter pode ser encontrado aqui. Sequencialmente, partindo do segmento mais curto de um ano, depois dois anos, três, etc., reconstruí a curva para um intervalo de até 10 anos. Esta é a minha curva de desconto que posso usar para avaliar qualquer instrumento. Esse método é chamado de bootstrap: o segmento da curva, que contei no início, uso na segunda etapa, caso contrário,o que consegui na segunda etapa, utilizo para a terceira etapa e assim por diante, até que a curva esteja completamente formada.

Espero que agora você não “flutue” mais no tema das taxas de juros flutuantes e entre as taxas de juros dos swaps você pode encontrar o vanilla. E você também pode construir qualquer curva usando o método bootstrap.

Todos os artigos desta série

Construção da curva de desconto. Programa educacional para um geek, parte 5

More articles: