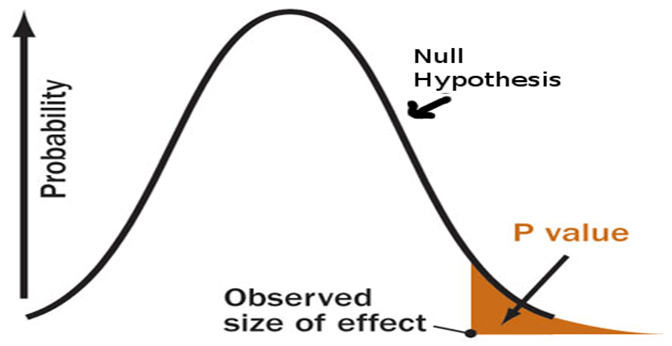
Na época, eu não sabia nada sobre valor p, teste de hipóteses ou mesmo significância estatística.
Decidi pesquisar no Google a palavra "p-value" e o que encontrei na Wikipedia me deixou ainda mais confuso ...
Ao testar hipóteses estatísticas, o valor p ou valor de probabilidade para um determinado modelo estatístico é a probabilidade de que, se a hipótese nula for verdadeira, o resumo estatístico (por exemplo, o valor absoluto da média da amostra da diferença entre dois grupos de comparação) será maior ou igual aos resultados reais observados.Bom trabalho, Wikipedia.
- Wikipedia
OK. Não entendi o que realmente significa o valor p.
À medida que me aprofundava no campo da ciência de dados, finalmente comecei a entender o significado do valor p e onde ele pode ser usado como parte das ferramentas de tomada de decisão em certos experimentos.
Portanto, decidi explicar o valor p neste artigo, bem como como ele pode ser usado em testes de hipótese, para dar a você um entendimento melhor e mais intuitivo dos valores p.
Também não podemos perder uma compreensão fundamental de outros conceitos e da definição de p-valor, prometo que farei esta explicação intuitiva sem expor você a todos os termos técnicos que me deparei.
Existem quatro seções no total neste artigo para fornecer uma visão completa, desde a construção de um teste de hipótese até a compreensão do valor p e sua utilização no processo de tomada de decisão. Eu recomendo fortemente que você passe por todos eles para obter uma compreensão detalhada dos valores-p:
- Testando hipóteses
- Distribuição normal
- O que é um valor P?
- Significado estatístico
Será divertido.
Vamos começar!
1. Testando hipóteses
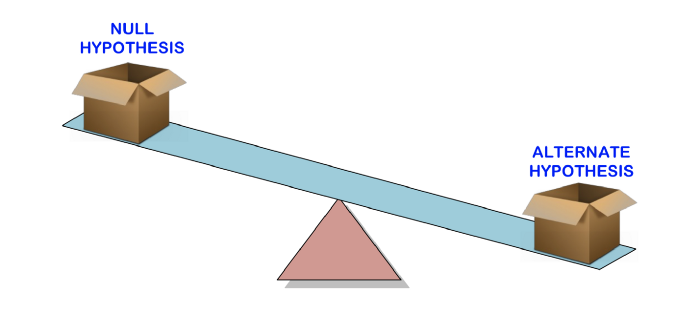
Antes de falarmos sobre o que significa valor p, vamos começar examinando o teste de hipótese , onde o valor p é usado para determinar a significância estatística de nossos resultados.
Nosso objetivo final é determinar a significância estatística de nossos resultados.
E a significância estatística baseia-se nestas 3 ideias simples:
- Testando hipóteses
- Distribuição normal
- Valor P
O teste de hipótese é usado para testar a validade de uma afirmação (hipótese nula) feita sobre uma população usando dados de amostra. Uma hipótese alternativa é aquela em que você acreditaria se a hipótese nula estivesse errada.
Em outras palavras, vamos criar uma reclamação (hipótese nula) e usar os dados da amostra para verificar se a reclamação é válida. Se a afirmação não for verdadeira, escolheremos uma hipótese alternativa. Tudo é muito simples.
Para descobrir se uma afirmação é válida ou não, usaremos o valor p para pesar a força da evidência e ver se ela é estatisticamente significativa. Se a evidência apoiar a hipótese alternativa, rejeitamos a hipótese nula e aceitamos a hipótese alternativa. Isso será explicado na próxima seção.
Vamos usar um exemplo para tornar esse conceito mais claro, e esse exemplo será usado ao longo deste artigo para outros conceitos.
Exemplo. Suponha que uma pizzaria alega ter um tempo médio de entrega de 30 minutos ou menos, mas você acha que é mais longo do que o declarado. Então, você faz um teste de hipótese e seleciona aleatoriamente um prazo de entrega para testar a reclamação:
- — 30
- — 30
- , , — — , .
Usaremos um teste unilateral no nosso caso, pois só é importante para nós que o tempo médio de entrega seja superior a 30 minutos. Não consideraremos essa possibilidade no outro sentido, pois as consequências do tempo médio de entrega ser menor ou igual a 30 minutos são ainda mais preferíveis. Queremos verificar aqui se existe a possibilidade de o tempo médio de entrega ser superior a 30 minutos. Em outras palavras, queremos ver se a pizzaria nos enganou.
Uma das maneiras comuns de testar hipóteses é usar o teste Z. Não entraremos em detalhes aqui, pois queremos entender melhor o que está acontecendo na superfície antes de mergulhar mais fundo.
2. Distribuição normal
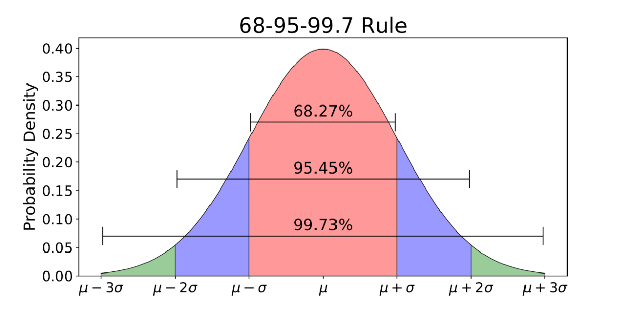
A distribuição normal é uma função de densidade de probabilidade usada para visualizar a distribuição de dados.
A distribuição normal possui dois parâmetros, a média (μ) e o desvio padrão, também chamado de sigma (σ).
A média é a tendência central na distribuição. Ele define a localização do pico para distribuições normais. O desvio padrão é uma medida de variabilidade. Determina a que distância da média os valores tendem a cair.
A distribuição normal geralmente está associada à regra 68-95-99,7 (imagem acima).
- 68% dos dados estão dentro de 1 desvio padrão (σ) da média (μ)
- 95% dos dados estão dentro de 2 desvios padrão (σ) da média (μ)
- 99,7% dos dados estão dentro de 3 desvios padrão (σ) da média (μ)
Lembra-se do limite de cinco sigma para o bóson de Higgs de que falei no início? 5 sigma é cerca de 99,999999426696856% dos dados que devem ser recebidos antes que os cientistas confirmem a descoberta do bóson de Higgs. Este foi um limite estrito definido para evitar quaisquer possíveis sinais falsos.
Legal. Agora você pode estar se perguntando: "Como a distribuição normal se relaciona com nosso teste de hipótese anterior?"
Como usamos o teste Z para testar nossa hipótese, precisamos calcular os escores Z (que serão usados em nossas estatísticas de teste), que são o número de desvios padrão da média do ponto de dados. No nosso caso, cada ponto de dados é o tempo de entrega da pizza que recebemos. Observe que quando calculamos todas as pontuações Z para cada tempo de entrega de pizza e traçamos uma curva de distribuição normal padrão conforme mostrado abaixo, a unidade no eixo X mudará de minutos para a unidade de desvio padrão conforme padronizamos a variável subtraindo a média e dividindo é pelo desvio padrão (veja a fórmula acima). Examinar a curva padrão do sino é útil porque podemos comparar os resultados do teste com uma população “normal” com uma unidade padronizada no desvio padrão, especialmente quando temos uma variável que vem com unidades diferentes.

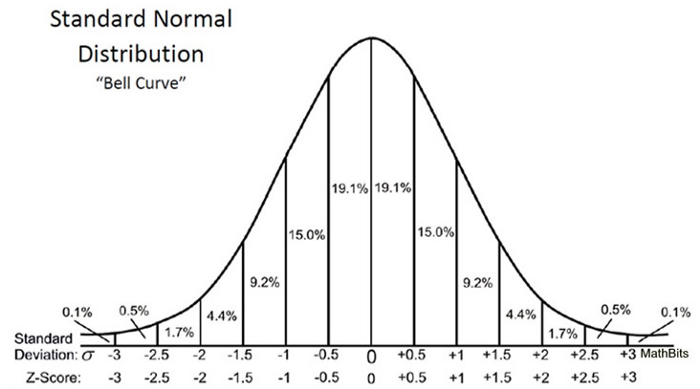
Uma pontuação z pode nos dizer onde estão os dados gerais em comparação com a população média.
Gosto da maneira como Will Cursen colocou: quanto mais alto ou mais baixo o Z-score, menos provável será um resultado aleatório e mais provável será um resultado significativo.
Mas quão alto (ou baixo) é considerado atraente o suficiente para quantificar o quão significativos são nossos resultados?
Clímax
Aqui, precisamos da última peça para resolver o quebra-cabeça, o valor p, e verificar se nossos resultados são estatisticamente significativos com base no nível de significância (também conhecido como alfa) que definimos antes de iniciar nosso experimento.
3. O que é valor P?
Finalmente ... Estamos falando de valor p aqui!
Todas as explicações anteriores têm como objetivo definir o cenário e nos levar a esse valor P. Precisamos do contexto e das etapas anteriores para entender esse valor-p misterioso (na verdade, não tão misterioso) e como ele pode levar às nossas decisões de testar a hipótese.
Se você veio até aqui, continue lendo. Porque esta seção é a parte mais emocionante de todas!
Em vez de explicar os valores-p usando a definição da Wikipedia (desculpe, Wikipedia), vamos explicar em nosso contexto - tempo de entrega da pizza!
Lembrando que selecionamos aleatoriamente alguns prazos de entrega de pizza, e o objetivo é verificar se o prazo de entrega ultrapassa 30 minutos. Se a evidência final apoiar a alegação da pizzaria (o tempo médio de entrega é de 30 minutos ou menos), não rejeitaremos a hipótese nula. Caso contrário, refutamos a hipótese nula.
Portanto, a função do valor p é responder a esta pergunta:
Se eu moro em um mundo onde os tempos de entrega de pizza são de 30 minutos ou menos (a hipótese nula está correta), quão inesperada é minha evidência na vida real?O valor P responde a essa pergunta com um número - uma probabilidade.
Quanto menor o valor de p, mais inesperada a evidência é, e mais ridícula parece nossa hipótese nula.
E o que fazemos quando nos sentimos ridículos sobre nossa hipótese nula? Nós o rejeitamos e escolhemos nossa hipótese alternativa.
Se o valor p estiver abaixo de um determinado nível de significância (as pessoas chamam de alfa, eu chamo isso de limite do absurdo - não pergunte por quê, é apenas mais fácil de entender), então rejeitamos a hipótese nula.
Agora entendemos o que significa valor p. Vamos aplicar isso em nosso caso.
Valor P no cálculo do tempo de entrega de pizza
Agora que coletamos alguns dados de amostra sobre os tempos de entrega, fizemos o cálculo e descobrimos que o tempo médio de entrega é 10 minutos a mais com um valor p de 0,03.
Isso significa que, em um mundo onde o tempo de entrega da pizza é de 30 minutos ou menos (a hipótese nula está correta), há uma chance de 3% de vermos o tempo médio de entrega pelo menos 10 minutos a mais devido ao ruído aleatório. ...
Quanto menor for o valor p, mais significativo será o resultado, porque é menos provável que seja causado por ruído.
Em nosso caso, a maioria das pessoas entende mal o valor p:
Um valor p de 0,03 significa que há 3% (probabilidade percentual) de que o resultado é devido ao acaso - o que não é verdade.Muitas vezes as pessoas querem uma resposta definitiva (inclusive eu), e é por isso que me confundi por muito tempo com a interpretação dos valores-p.
O valor p não * prova * nada. É apenas uma forma de usar a surpresa como base para uma decisão inteligente.Veja como podemos usar um valor p de 0,03 para nos ajudar a tomar decisões inteligentes (IMPORTANTE):
- Cassie Kozyrkov
- Imagine que vivemos em um mundo onde o tempo médio de entrega é sempre de 30 minutos ou menos - porque acreditamos na pizzaria (nossa crença original)!
- Depois de analisar o tempo de entrega das amostras coletadas, o valor de p é 0,03 menor que o nível de significância de 0,05 (assumindo que definimos esse valor antes de nosso experimento) e podemos dizer que o resultado é estatisticamente significativo.
- , 30 , , , , .
- ? ( ) . , , , , , , .
- , — .
Agora, você deve ter descoberto algo ... Dependendo do nosso contexto, os valores-p não são usados para provar ou justificar nada.
Na minha opinião, os valores de p são usados como uma ferramenta para desafiar nossa crença inicial (hipótese nula) quando o resultado é estatisticamente significativo. No momento em que nos sentimos ridículos com nossa própria crença (assumindo que o valor p indica que o resultado é estatisticamente significativo), descartamos nossa crença original (rejeitamos a hipótese nula) e tomamos uma decisão inteligente.
4. Significância estatística
Por fim, esta é a última etapa em que juntamos tudo e verificamos se o resultado é estatisticamente significativo.
Não é suficiente ter apenas um valor de p, precisamos definir um limite (nível de significância - alfa). Alfa deve sempre ser definido antes de experimentar para evitar viés. Se o valor de p observado for inferior a alfa, concluímos que o resultado é estatisticamente significativo.
A regra básica é definir alfa como 0,05 ou 0,01 (novamente, o valor depende da sua tarefa).
Conforme mencionado anteriormente, suponha que definimos o alfa como 0,05 antes de iniciarmos o experimento, o resultado é estatisticamente significativo, pois o valor p de 0,03 é menor do que o alfa.
Para sua referência, abaixo estão as principais etapas de todo o experimento:
- Formule a hipótese nula
- Forme uma hipótese alternativa
- Determine o valor alfa a ser usado
- Encontre a pontuação Z associada ao seu nível alfa
- Encontre estatísticas de teste usando esta fórmula
- Se a estatística de teste for menor que o valor alfa Z (ou o valor p for menor que o valor alfa), rejeite a hipótese nula. Caso contrário, não rejeite a hipótese nula.
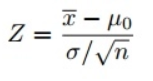
Se você quiser aprender mais sobre significância estatística, sinta-se à vontade para verificar este artigo - Explicando a Significância Estatística , escrito por Will Kersen .
Reflexões subsequentes
Há muito para digerir aqui, não é?
Não posso negar que os valores-p são inerentemente confusos para muitas pessoas, e demorei um pouco para realmente entender e apreciar os valores-p e como eles podem ser aplicados em nosso processo de tomada de decisão. como cientistas de dados.
Mas não confie muito nos valores-p, pois eles ajudam apenas em uma pequena parte de todo o processo de tomada de decisão.
Espero que minha explicação dos valores p tenha se tornado intuitiva e útil para você compreender o que os valores p realmente significam e como eles podem ser usados para testar suas hipóteses.
O cálculo dos valores p é simples por si só. A parte difícil surge quando queremos interpretar os valores p em testes de hipóteses. Esperançosamente, agora a parte difícil se torna um pouco mais fácil para você.
Se você quiser aprender mais sobre estatística, recomendo fortemente que você leia este livro (que estou lendo no momento!) - Estatísticas Práticas para Cientistas de Dados, especialmente escrito para cientistas de dados entenderem os conceitos fundamentais da estatística.

Saiba mais sobre como obter uma profissão de alto perfil do zero ou Subir de nível em habilidades e salários, fazendo os cursos online pagos da SkillFactory:
- Treinando a profissão de Ciência de Dados do zero (12 meses)
- Profissão de analista em qualquer nível inicial (9 meses)
- Machine Learning (12 )
- «Python -» (9 )
- DevOps (12 )
- - (8 )
- Data Sciene 2020
- Data Science . Business Science
- Data Scientist
- Data Scientist -
- 450
- Data Science : «data»
- Data Sciene : Decision Intelligence