Outros artigos do ciclo
Após uma apresentação detalhada com detalhes de transformações individuais, com elementos de um campo algébrico finito, não abstrato (como em muitas publicações, não excluindo o Khabrovsky), mas ( concreto ), dentro do qual RIJNDAEL, AES-128 e ( executando operações do padrão AES-128 ) são implementados , podemos passar a considerar possíveis ataques à cifra. Por enquanto, vamos nos restringir a um ataque, em nossa opinião, o mais compreensível e transparente construído (embora, talvez, não para todos os leitores) Habr.
Já estou acostumada com as desvantagens, mas do que diabo não está brincando. A análise de possíveis ataques e resultados esperados foi realizada por muitos autores, mas exemplos concretos de sucesso ou designs simplesmente impressionantes claramente não são suficientes. Aqui, consideraremos de um ponto de vista matemático um ataque usando um erro introduzido pelo intruso no texto cifrado. Ao escolher um ataque para uma demonstração, o autor procurou não envolver aqueles em que se utilizam coisas matemáticas muito distorcidas e confusas, mas o assunto em questão em si é bastante sério e não permite passar para as explicações nos "dedos".
Um objetivo importante da publicação é mostrar a aplicação da matemática, que constitui a base do AES-128, e que, infelizmente, muitos autores contornam ou interpretam mal o infundado e não substanciado, guiados pelo fato de que poucos podem verificar e apontar suas invenções.
O material do artigo não é totalmente o conceito original do ataque, as principais ações são retiradas do trabalho , mas foi cuidadosamente elaborado, complementado e testado experimentalmente pelos meus alunos. Eles têm boas práticas em álgebra superior e criptologia.
1. Ataque à chave de cifra AES
Primeiro, um ataque ao AES é descrito em um caso simples e, em seguida, fica claro como esse ataque pode ser generalizado. O objetivo do ataque em consideração é recuperar a chave K (Nr) da cifra. Uma vez que a chave parcial (redonda) K (Nr) é determinada, torna-se fácil obter a chave K.
1.1 Princípio de ataque
Supõe-se que é possível mudar introduzindo o erro "ε" em um byte separado da matriz S do estado (um de 16) após a operação ShiftRows (Nr - 1), ou seja, a penúltima rodada e o índice (# da célula) do byte corrompido (elemento ) Estado. Esta última hipótese pode ser omitida, foi introduzida para explicar mais facilmente o mecanismo de ataque. O novo valor do item de estado é considerado desconhecido.
O erro "ε" se estende a não mais que quatro bytes do status de saída do processo. Para todos os 4 elementos mutáveis do estado de saída, um conjunto de valores (conjunto) de vetores de possível erro "ε" é encontrado na seção 1.4. Além disso, torna-se possível cruzar os conjuntos de valores possíveis "ε" (definição 1) para esses quatro elementos. Quando esses conjuntos se cruzam, um conjunto menor é obtido e, portanto, o número de textos criptografados necessários para a análise completa é reduzido.
Finalmente, para cada erro, imprimimos alguns valores deturpados possíveis para os quatro elementos da chave da rodada anterior. Formando outros textos cifrados, encontramos quatro bytes da chave redonda K (10). Este ataque continua bem-sucedido mesmo com muitas suposições gerais sobre a localização do erro. Como a falta de informação sobre a localização do erro antes da 9ª transformação MixColumns (). A diferença entre a matriz do texto cifrado com e sem distorções revelará as distorções e sua posição (no exemplo, são as posições 0,7,10,13).
Também é assumido que os erros "ε" introduzidos na rodada 8 (antes da 8ª transformação MixColumns ()) podem ser úteis para a análise. Mas, ao mesmo tempo, aumenta o número de textos cifrados necessários para uma análise mais completa. Para o exemplo numérico em consideração, cerca de dez textos cifrados são necessários para obter quatro bytes da chave redonda K (10), sob condições em que a hipótese de localização de erros não é considerada.
1.2 Exemplo numérico do impacto de um erro em uma mensagem
Aqui, o mesmo exemplo é usado conforme fornecido no Apêndice da obra mencionada . São consideradas as penúltimas e últimas rodadas do processo de criptografia (a representação em bytes dos dados tem a forma):
Input = '32 43 F6 A8 88 5A 30 8D 31 31 98 A2 E0 37 07 34 ';
Chave de cifra = '2B 7E 15 16 28 AE D2 A6 AB F7 15 88 09 CF 4F 3C';
Saída = '39 25 84 1D 02 DC 09 FB DC 11 85 97 19 6A 0B 32 ';
Erro "ε" = '1E 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00'.
O diagrama a seguir mostra os valores contidos nas matrizes de estado de acordo com o comprimento do bloco de criptografia e o comprimento da chave de criptografia de 16 bytes cada (ou seja, Nb = 4 e Nk = 4).
A propagação do erro é mostrada em negrito e hexadecimal. Abaixo estão as praças do Estado em diferentes situações:
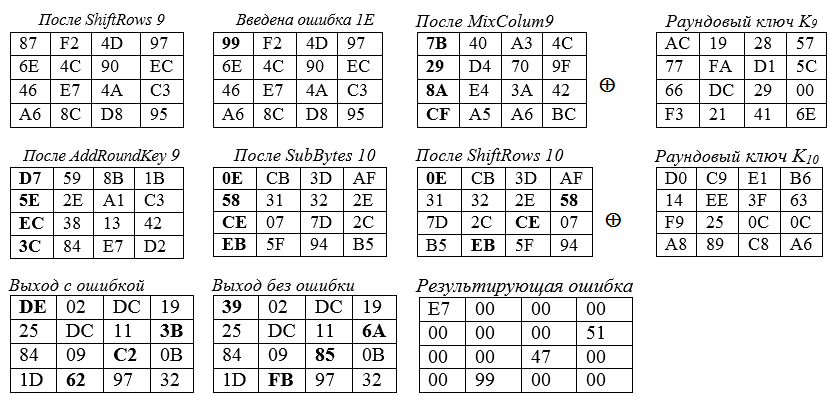
O erro "ε" = 1E, inserido no 0º byte do estado da 9ª rodada, resulta em alterações nos quatro bytes do estado final. Exemplos de cálculos para as células do canto da diagonal principal do "quadrado" do estado:
- o erro "ε" = 1E
87 ⊕ 1E = 1000 0111⊕ 0001 1110 = 1001 1001 = 99
é inserido na célula superior esquerda (canto) do quadrado do estado da 9ª rodada - inferior direito O estado do ângulo da 9ª rodada após MixColum9 é resumido com o byte de chave K (9):
BC ⊕ 6E = 1011 1100⊕ 0110 1110 = 1101 0010 = d2.
- calcular os valores do erro resultante.
Na presença de dois textos de mensagem, com e sem erro, os valores e posições dos bytes de status corrompidos são determinados subtraindo um texto do outro. Em nosso caso, essa subtração pode ser substituída pela soma dos textos módulo dois. Obtemos um resultado diferente de zero apenas para bytes alterados por um erro introduzido no texto de origem.
Por exemplo, na forma hexadecimal, encontramos os valores de erro:
Tabela 7 - cálculo dos valores de erro
Como resultado, os erros de diferença... Vamos dar um exemplo de cálculo do último byte de erro:
62 ⊕ FB = 01100010 ⊕11111011 = 1001 1001 = 99.
Posições dos bytes de status alteradas pelo erro
.indique os índices para os elementos da chave redonda (última rodada), como K [0], K [7], K [10], K [13]. Aqui, 0, 7, 10, 13 são os números das células da matriz de estado, e a matriz Ao é a matriz de transformação para misturar as colunas do processo de criptografia, cuja primeira coluna tem a forma: '02', '01', '01', '03'.
Como um erro injetado afeta o estado final final
Análise das informações obtidas quando um erro é introduzido
A única operação que pode conter informações sobre a chave K (Nr) é a última transformação SubBytes (). Portanto, temos quatro equações, onde x0, x1, x2, x3, ε são variáveis desconhecidas.
Queremos obter soluções para as quatro equações a seguir:
Bytes modificados por um erro contêm informações sobre a chave desconhecida que gerou esses bytes.
Todas essas equações podem ser generalizadas em uma única equação
s (x + cε) + s (x) = ε ', (1)
onde o valor constante =' 01 ',' 02 'ou' 03 'e é esta equação que iremos resolver posteriormente e analisar.
Definição 1 . O conjunto de soluções da equação (1) para erros ε é denotado pelo símbolo B (cε ') e definido pela expressão:
B (cε') = S (cε ') = {ε є GF [2 8 ]: ∃ x є GF [2 8 ], s (x + cε) + s (x) = ε '}, | B (cε') | = 127.
Esta é uma área de erro individual correspondente a um erro específico ε '. Para outros ε ', as regiões de erro serão diferentes.
Definição 2 . Considere uma transformação linear ℓ sobre o campo GF (2):
ℓ: GF [2 8 ] → GF [2 8 ];
x → x 2 + x.
A imagem de ℓ é um mapeamento do espaço vetorial Im (ℓ) GF (2), ou seja, o conjunto de elementos
(x 2 + x) de GF [2 8 ] denotamos 1 = Im (ℓ) e sua dimensão dimGF (2) (E1) = 7. Se θ є 1, então há duas soluções diferentes x1, x2 є GF [ 2 8 ] equações x 2 + x = θ, e as soluções satisfazem a relação x2 = x1 + 1 e x2 ∙ x1 = θ (modd φx, (2 8 -1)) pelo teorema de Vieta.
A variável θ é um termo livre de uma equação quadrática,
vamos ilustrar a transformação linear considerada com um exemplo.
Exemplo O campo GF é definido [2 8], a transformação x → x 2 + x é realizada sobre seus elementos .
Tabela 8 - o fragmento inicial do campo GF [2 8 ] e os resultados da transformação dos elementos.
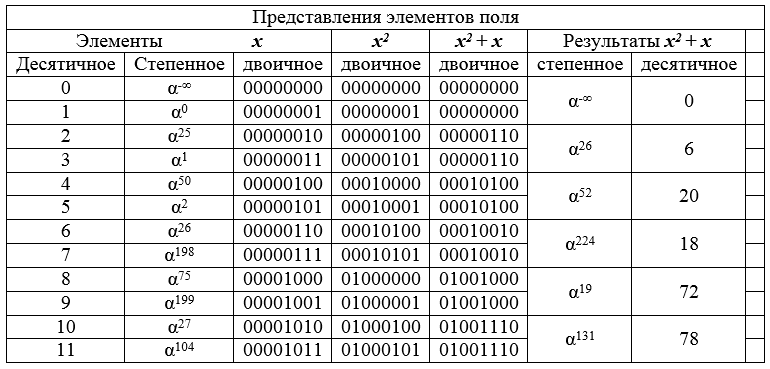
A Tabela 8 mostra como a transformação muda pares adjacentes em uma lista decimais para o mesmo elemento de campo. Conclui-se que o resultado da transformação (imagem) é duas vezes menor que a imagem inversa (o campo é, por assim dizer, comprimido 2 vezes). Este princípio de contração da dimensão dos conjuntos forma a base do ataque proposto.
Proposição 2 . A seguinte afirmação é verdadeira para λ1, λ2 є GF [2 8 ] - {0}:
2. Generalização e implementação
Em primeiro lugar, com a ajuda de um aplicativo de software especial, são gerados 20 textos cifrados com erro. Para fazer isso, o texto-fonte, a chave, o erro são inseridos no modelo (programa) e o número da posição em que o erro é colocado é definido. Ao pressionar o botão "Iniciar", o programa implementa o algoritmo e exibe os resultados das últimas 2 rodadas de criptografia em forma expandida para texto com erro, texto sem erro e a diferença entre eles. Depois disso, o texto cifrado é salvo sem erro e com erro. O valor do erro é alterado ciclicamente e pressionando o botão "Iniciar" o próximo texto cifrado com um erro é obtido. Em um valor da coluna, 5 textos cifrados com um erro foram formados.
Para implementar o ataque, você deve abrir um arquivo com texto cifrado sem erro e texto cifrado com erro usando o programa (os dados do arquivo são apresentados na forma hexadecimal), os textos cifrados e a diferença entre eles são exibidos como uma matriz quadrada de bytes (Estado). Pressionando o botão “Buscar chave” inicia-se o procedimento de busca de possíveis bytes da chave. O estado atual dos processos é exibido em uma caixa de texto. Em seguida, um texto cifrado com outro erro é aberto e o procedimento é repetido. Quando um byte de chave redonda 10 é recebido, ele também é exibido na matriz quadrada de bytes correspondente. Ao executar todos os 20 textos cifrados gerados na etapa anterior com um erro, há uma grande probabilidade de obter os valores de todos os bytes da chave rodada 10 (caso contrário, textos cifrados com erros também são necessários).Depois disso, restaure a chave de criptografia de acordo com o algoritmo "Cipher key recovery using the last subkey" fornecidoaqui .
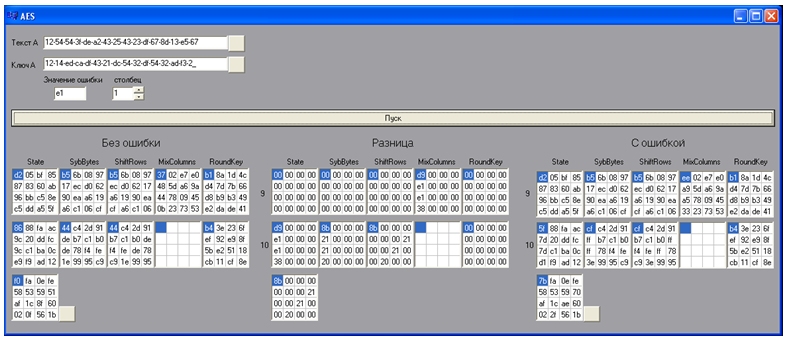
Figura 11 - Produto de software para construir um texto cifrado com erro
Para acelerar o procedimento de enumeração do texto cifrado com erro, você pode marcar ao lado do botão "Localizar chave"
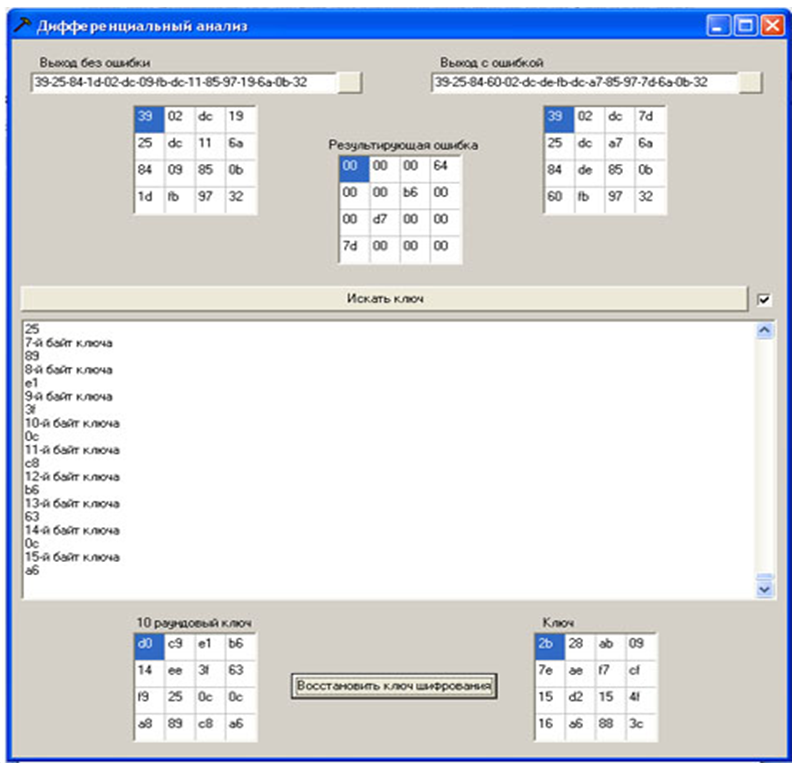
Figura 12 - Implementação de software de um ataque
Um exemplo de produto de software:
Código-fonte 3243f6a8885a308d313198a2e0370734
Chave 2b7e151628aed2a6abf7158809cf4f3c
Erro 1 1e0000000000000000000000000000000000 Texto cifrado
com erro 1
Possíveis bytes de250941dbdc
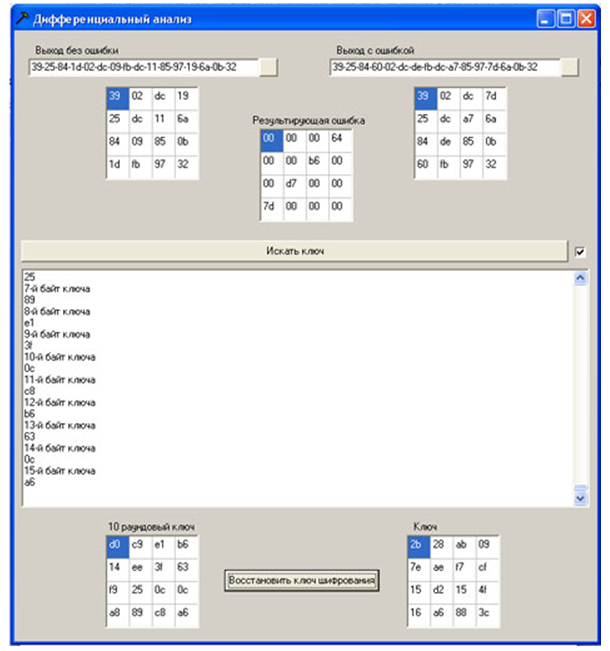
Figura 13 - Um exemplo da operação do programa
Chave da rodada 10 d014f9a8c9ee2589e13f0cc8b6630ca6 a chave está totalmente recuperada A
chave recuperada 2b7e151628aed2a6abf7158809cf4f3c, conforme esperado, corresponde à chave especificada na sessão de criptografia.
2.1. Situação em que não há informações de localização de erro
Neste ponto, assume-se que o erro está no byte de status entre as duas últimas execuções da operação MixColumns. Este é o mesmo caso, exceto pelo fato de que o erro pode estar entre bytes de 1 a 16. O erro é multiplicado pela operação MixColumns e se espalha para 4 bytes de status.
O erro forçado é gerado na primeira linha da matriz de estado diferencial. Aqui é possível determinar a qual coluna o erro inserido pertence, observando a coluna de erro forçado. Isso é feito examinando as quatro posições de linha possíveis para o erro inserido usando o método descrito na descrição anterior.
2.2. Dispositivo de hardware
Vamos supor que você tenha a capacidade de interferir fisicamente em um dispositivo de hardware AES. Primeiro, vamos calcular cifras para mais de dez textos simples aleatórios usando um dispositivo AES. Em seguida, mudamos o projeto de exemplo cortando as linhas e conectando-as ao solo (ou Vcc) temporariamente entre dois bytes durante a rodada, localizados duas rodadas antes da conclusão. Afinal, temos um byte no round Nk -2, sempre substituído por '00' (ou 'FF').
Calculamos outra vez a mesma mensagem com o dispositivo de atuação. Com o texto simples aleatório, um byte defeituoso é como um erro aleatório. Este único erro se traduz em quatro erros na rodada Nk -1 e dezesseis erros na rodada Nk. Nesse caso, pode-se obter uma matriz de desvio (diferencial), com a qual é possível, analisando o erro, encontrar a chave de última rodada.
Literatura:
[1] FIPS PUB 197: Padrão de criptografia avançada, csrc.nist.gov/publications/fips/fips197/fips-197.pdf
[2] Boneh, DeMillo e Lipton, Sobre a importância da verificação de protocolos criptográficos para falhas, Lecture Notes in Computer Science, Advances in Cryptology, procedures of EU-ROCRYPT'97, pp. 37-51, 1997.
[3] E. Biham & A. Shamir, Differential Fault Analysis of Secret Key Cryptosystems, CS 0910, Proceedings of Crypto'97.
[4] Ross J. Anderson, Markus G. Kuhn: Tamper Resistance - a Cautionary Note, The Second USENIX Workshop on Electronic Commerce Proceedings, Oakland, Califórnia, 18-21 de novembro de 1996, pp 1-11, ISBN 1-880446- 83-9.