Introdução
A arquitetura da Rede Neural Convolucional (CNN) RetinaNet consiste em 4 partes principais, cada uma com seu próprio objetivo:
a) Backbone - a rede principal (básica) usada para extrair recursos da imagem de entrada. Essa parte da rede é variável e pode incluir redes neurais de classificação como ResNet, VGG, EfficientNet e outras;
b) Rede de pirâmide de recursos (FPN) - uma rede neural convolucional construída na forma de uma pirâmide, que serve para combinar as vantagens dos mapas de recursos dos níveis inferior e superior da rede; os primeiros têm alta resolução, mas baixa capacidade de generalização semântica; o último, pelo contrário;
c) Sub-rede de classificação - uma sub-rede que extrai informações sobre classes de objetos do FPN, resolvendo o problema de classificação;
d) Sub-rede de regressão - uma sub-rede que extrai informações sobre as coordenadas dos objetos na imagem do FPN, resolvendo o problema de regressão.
Na fig. 1 mostra a arquitetura do RetinaNet com a rede neural ResNet como espinha dorsal.
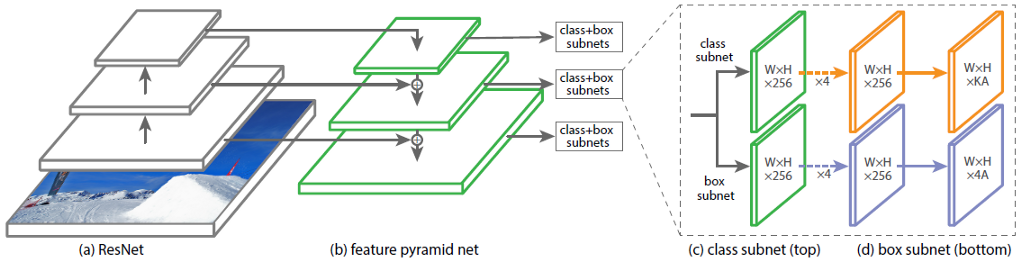
Figura 1 - Arquitetura do RetinaNet com um backbone ResNet
Vamos analisar em detalhes cada uma das partes do RetinaNet mostradas na Fig. 1
O backbone faz parte da rede RetinaNet
Considerando que a parte da arquitetura RetinaNet que aceita uma imagem como entrada e destaca recursos importantes é variável e as informações extraídas dessa parte serão processadas nas próximas etapas, é importante escolher uma rede de backbone apropriada para obter os melhores resultados.
Pesquisas recentes sobre otimização da CNN levaram ao desenvolvimento de modelos de classificação que superam todas as arquiteturas desenvolvidas anteriormente com as melhores taxas de precisão no conjunto de dados ImageNet, além de melhorar a eficiência em 10 vezes. Essas redes foram nomeadas EfficientNet-B (0-7). Os indicadores da família de novas redes são mostrados na Fig. 2.
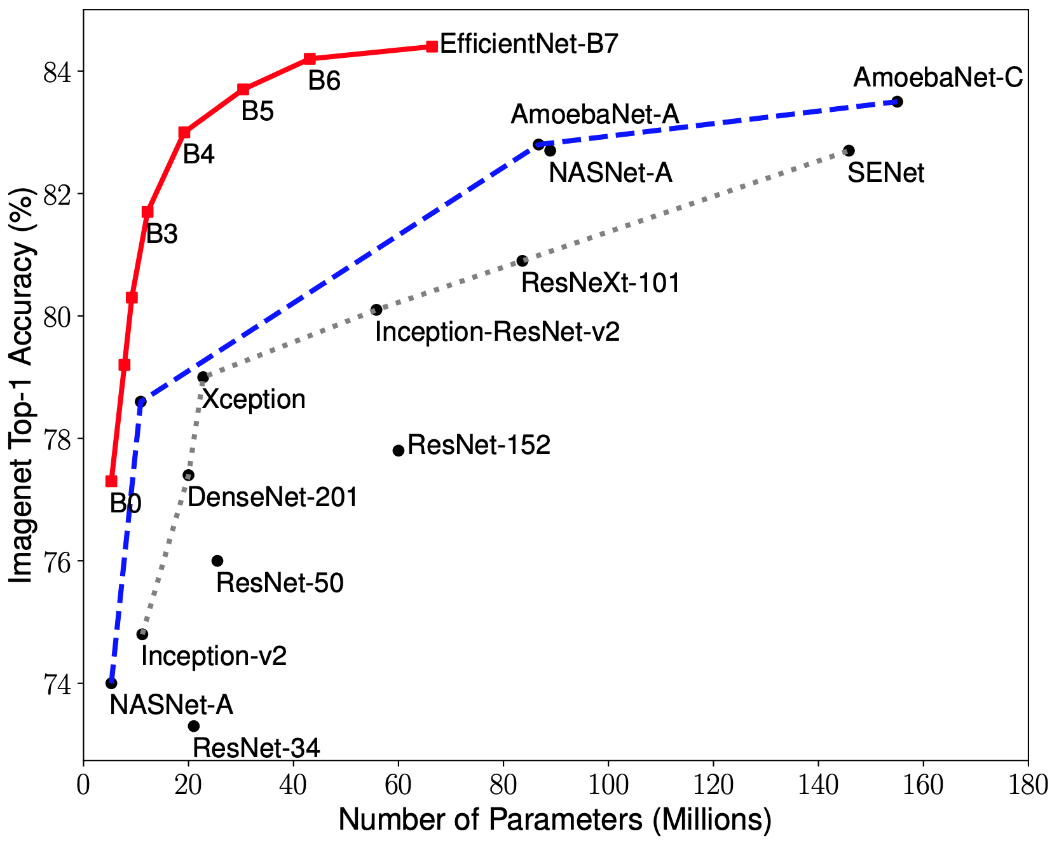
Figura 2 - Gráfico da dependência do indicador de maior precisão no número de pesos de rede para várias arquiteturas
A pirâmide de sinais
A Rede de pirâmides de recursos consiste em três partes principais: caminho de baixo para cima, caminho de cima para baixo e conexões laterais.
O caminho ascendente é uma espécie de "pirâmide" hierárquica - uma sequência de camadas convolucionais com dimensão decrescente, no nosso caso - uma rede de backbone. As camadas superiores da rede convolucional têm mais significado semântico, mas menor resolução e as inferiores, pelo contrário (Fig. 3). O caminho de baixo para cima tem uma vulnerabilidade na extração de recursos - a perda de informações importantes sobre um objeto, por exemplo, devido ao ruído de um objeto pequeno, mas significativo em segundo plano, pois no final da rede as informações são altamente compactadas e generalizadas.
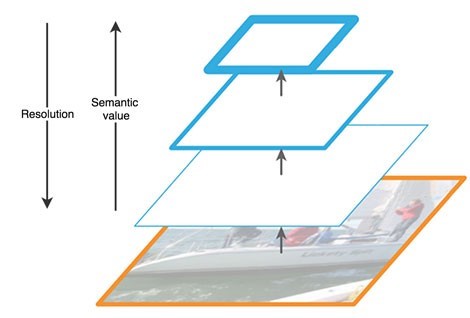
Figura 3 - Recursos dos mapas de recursos em diferentes níveis da rede neural
O caminho descendente também é uma "pirâmide". Os mapas de características da camada superior desta pirâmide têm o tamanho dos mapas de características da camada superior da base para cima da pirâmide e são duplicados pelo método do vizinho mais próximo (Fig. 4) para baixo.
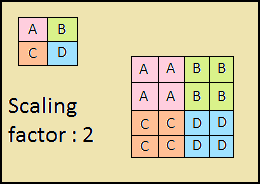
Figura 4 - Aumentando a resolução da imagem pelo método vizinho mais próximo
Assim, na rede descendente, cada mapa de características da camada sobreposta é aumentado para o tamanho do mapa subjacente. Além disso, as conexões laterais estão presentes no FPN, o que significa que os mapas de recursos das camadas de baixo para cima e de cima para baixo correspondentes das pirâmides são adicionados elemento por elemento, e os mapas de baixo para cima são dobrados 1 * 1. Este processo é mostrado esquematicamente na Fig. 5.
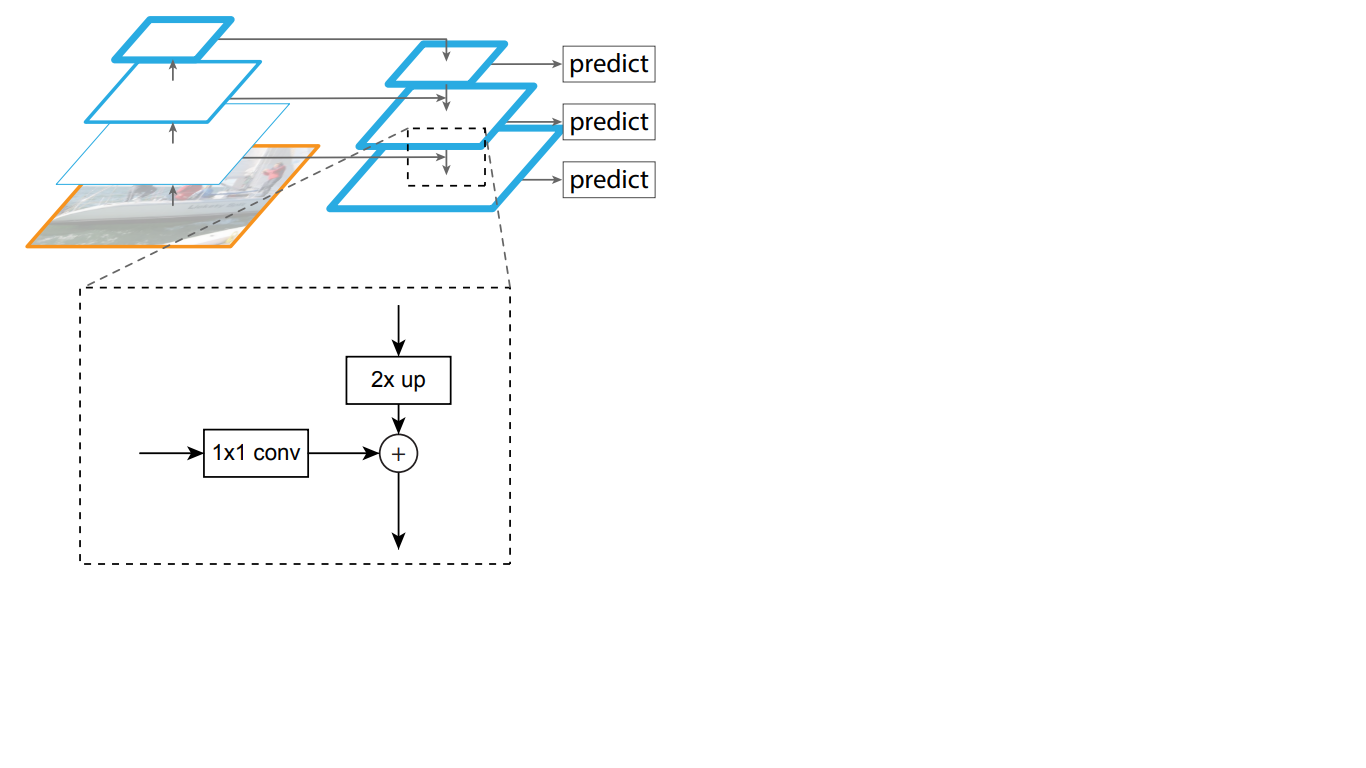
Figura 5 - A estrutura da pirâmide de signos
As conexões laterais resolvem o problema da atenuação de sinais importantes no processo de passagem pelas camadas, combinando informações semanticamente importantes recebidas no final da primeira pirâmide e informações mais detalhadas obtidas anteriormente.
Além disso, cada uma das camadas resultantes na pirâmide de cima para baixo é processada por duas sub-redes.
Sub-redes de classificação e regressão
A terceira parte da arquitetura do RetinaNet são duas sub-redes: classificação e regressão (Figura 6). Cada uma dessas sub-redes forma na saída uma resposta sobre a classe do objeto e sua localização na imagem. Vamos considerar como cada um deles funciona.

Figura 6 - Sub-redes RetinaNet
A diferença nos princípios dos blocos considerados (sub-redes) não difere até a última camada. Cada um deles consiste em 4 camadas de redes convolucionais. 256 mapas de recursos são formados na camada. Na quinta camada, o número de mapas de recursos é alterado: a sub-rede de regressão possui mapas de recursos 4 * A, a sub-rede de classificação possui mapas de recursos K * A, em que A é o número de quadros de âncora (descrição detalhada dos quadros de âncora na próxima subseção), K é o número de classes de objetos.
Na última, sexta camada, cada mapa de características é transformado em um conjunto de vetores. O modelo de regressão na saída possui para cada caixa âncora um vetor de 4 valores indicando o deslocamento da caixa terra-verdade em relação à caixa âncora. O modelo de classificação possui um vetor quente de comprimento K na saída para cada quadro de âncora, no qual o índice com o valor 1 corresponde ao número da classe que a rede neural atribuiu ao objeto.
Quadros de ancoragem
Na última seção, o termo quadros de ancoragem foi usado. A caixa âncora é um hiperparâmetro de detectores de redes neurais, um retângulo delimitado predefinido com relação ao qual a rede opera.
Digamos que a rede tenha um mapa de recursos 3 * 3 na saída. No RetinaNet, cada célula possui 9 caixas de ancoragem, cada uma com tamanho e proporção diferentes (Figura 7). Durante o treinamento, os quadros âncora são correspondidos a cada quadro de destino. Se o indicador IoU tiver um valor de 0,5, o quadro âncora será designado como destino, se o valor for menor que 0,4, será considerado o plano de fundo; em outros casos, o quadro âncora será ignorado para treinamento. A rede de classificação é treinada em relação à atribuição atribuída (classe de objeto ou plano de fundo), a rede de regressão é treinada em relação às coordenadas do quadro de âncora (é importante observar que o erro é calculado em relação ao quadro de âncora, mas não ao quadro de destino).
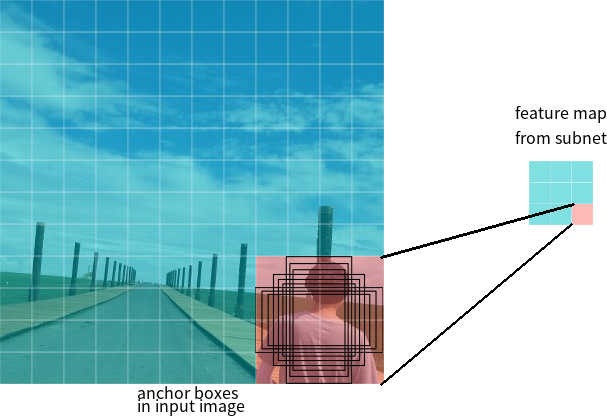
Figura 7 - Quadros âncora para uma célula do mapa de características com um tamanho de 3 * 3
Funções de perda
As perdas do RetinaNet são compostas, são compostas por dois valores: o erro de regressão ou localização (indicado como Lloc abaixo) e o erro de classificação (indicado como Lcls abaixo). A função de perda geral pode ser escrita como:
Onde λ é um hiperparâmetro que controla o equilíbrio entre as duas perdas.
Vamos considerar com mais detalhes o cálculo de cada uma das perdas.
Conforme descrito anteriormente, cada quadro de destino recebe uma âncora. Vamos denotar esses pares como (Ai, Gi) i = 1, ... N, onde A representa a âncora, G é o quadro de destino e N é o número de pares correspondentes.
Para cada âncora, a rede de regressão prevê 4 números, que podem ser indicados como Pi = (Pix, Piy, Piw, Pih). Os dois primeiros pares representam a diferença prevista entre as coordenadas dos centros da âncora Ai e o quadro alvo Gi, e os dois últimos representam a diferença prevista entre largura e altura. Assim, para cada quadro de destino, o Ti é calculado como a diferença entre os quadros de ancoragem e de destino:
Onde smoothL1 (x) é definido pela fórmula abaixo:
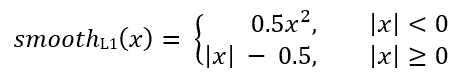
A perda do problema de classificação do RetinaNet é calculada usando a função de perda focal.
onde K é o número de classes, yi é o valor alvo da classe, p é a probabilidade de prever a i-ésima classe, γ é o parâmetro de foco, α é o coeficiente de polarização. Esse recurso é um recurso avançado de entropia cruzada. A diferença está na adição do parâmetro γ∈ (0, + ∞), que resolve o problema do desequilíbrio de classe. Durante o treinamento, a maioria dos objetos processados pelo classificador são em segundo plano, que é uma classe separada. Portanto, um problema pode surgir quando a rede neural aprende a determinar o plano de fundo melhor do que outros objetos. A adição de um novo parâmetro resolveu esse problema, reduzindo o valor do erro para objetos facilmente classificados. Os gráficos das funções de entropia focal e cruzada são mostrados na Fig. 8.
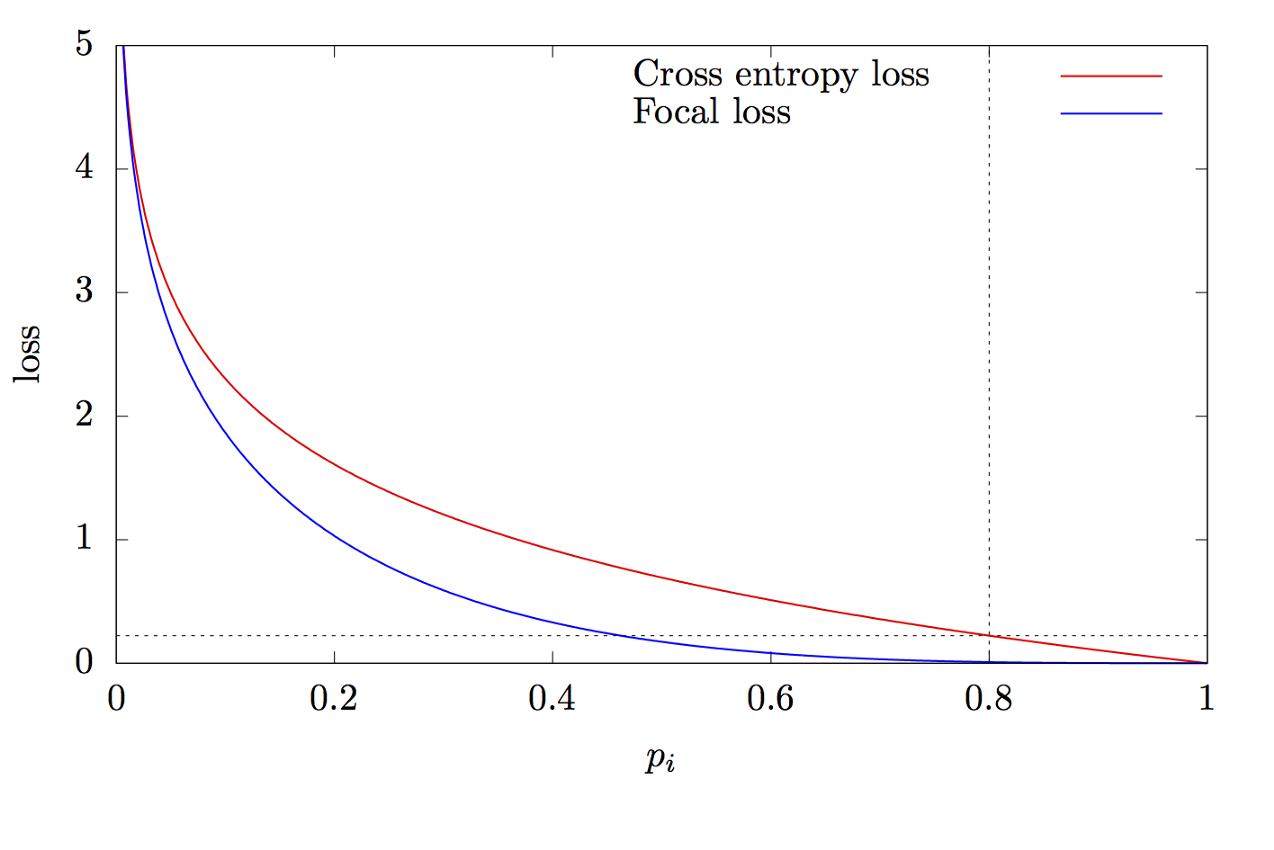
Figura 8 - Gráficos das funções de entropia focal e cruzada
Obrigado por ler este artigo!
Lista de fontes:
- Tan M., Le Q. V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. 2019. URL: arxiv.org/abs/1905.11946
- Zeng N. RetinaNet Explained and Demystified [ ]. 2018 URL: blog.zenggyu.com/en/post/2018-12-05/retinanet-explained-and-demystified
- Review: RetinaNet — Focal Loss (Object Detection) [ ]. 2019 URL: towardsdatascience.com/review-retinanet-focal-loss-object-detection-38fba6afabe4
- Tsung-Yi Lin Focal Loss for Dense Object Detection. 2017. URL: arxiv.org/abs/1708.02002
- The intuition behind RetinaNet [ ]. 2018 URL: medium.com/@14prakash/the-intuition-behind-retinanet-eb636755607d