
Outros artigos do ciclo
AES — . I
ES — . II
AES — . III
AES — . IV
AES — . V.
ES — . II
AES — . III
AES — . IV
AES — . V.
Nesta parte IV, concluímos a descrição da cifra AES-128. Para os leitores que não estão familiarizados com as partes anteriores do trabalho, explicarei que o material é apresentado para fins educacionais e isso impõe uma série de características (detalhes, exemplos numéricos, fundamentos matemáticos, etc.) , e o uso do material apresentado para o desenvolvimento de algoritmos de criptografia e descriptografia (na ausência de uma chave). Os autores de muitas publicações online (e offline) bem conhecidas não estabeleceram tais objetivos, o que torna essas publicações de pouca utilidade para nossos propósitos.
O processo reverso de criptografia é chamado de descriptografia de mensagens. Para descriptografar (com uma chave) os textos cifrados (ST), uma tabela de substituição inversa e chaves redondas são criadas, usadas em ordem inversa em relação ao esquema de criptografia, mas semelhante ao processo de criptografia.
Descriptografando mensagens AES
A lista de operações para descriptografar uma mensagem permanece a mesma da criptografia. Mais detalhes sobre as operações podem ser encontrados aqui . Esse é um princípio bastante geral das cifras - uma implementação de hardware única para criptografia e descriptografia, fornecida por conjuntos das mesmas funções para os dois processos. Somente o texto de origem e a sequência de envio das chaves são alterados.
O processo de decriptografar mensagens é implementado como uma sequência de transformações reversas (inversas) usadas para criptografia, na ordem inversa de sua sequência durante a criptografia. Também é óbvio que as teclas redondas são usadas na sequência apropriada: primeiro, a chave recebida por último, depois a penúltima, e assim por diante até a primeira tecla redonda.
Todos os nomes de transformação permanecem os mesmos, mas são prefixados com Inv. Vamos considerá-los na mesma sequência de antes. A cifra AES permite duas opções de descriptografia, reversa e direta, que são discutidas em detalhes abaixo.
Opção de descriptografia reversa
A descriptografia reversa de uma mensagem é um processo natural de reverter o processo de criptografia.
A operação AddRoundKey permanece a mesma (inalterada) S + Ki para todos os 16 bytes do Estado, como fazia ao criptografar a mensagem, ou seja, é o inverso de si mesmo. Isso se deve ao fato de a lógica XOR ser usada na operação e os bytes serem representáveis em números binários.
A chave da última rodada é simplesmente adicionada (resumida) à mensagem criptografada.
InvSubBytes. A essência dessa transformação não mudou, ou seja, cada byte da mensagem que está sendo convertida é substituído por outro extraído da tabela (S -1-block) substituição. Obviamente, a tabela de substituição é diferente aqui. O byte {x, y} é substituído pelo byte da Inv S (x, y) de acordo com o mesmo princípio: x - linha da tabela, y - sua coluna. O byte de substituição é recuperado da célula na interseção da linha (x) e da coluna (y) da tabela Inv S (x, y).
Como antes, o tamanho da tabela é 16 × 16 = 256 bytes, cada um dos quais é obtido por multiplicação e subtração de matriz vetorial (transformação afim) do produto do vetor de deslocamento C. Em campos binários, as operações de adição e subtração são equivalentes, portanto o vetor C pode ser simplesmente adicionado a produtos. A tabela InvSubBytes é mostrada abaixo. O nó especificado de substituições S -1 é apresentado na tabela 1 a seguir, os valores são apresentados em formato hexadecimal:
Tabela 1. Tabela de substituições do bloco inverso S -1 -

A tabela mostra exemplos de substituições de dois bytes 4A → 5C e 9F → 6E preenchidos com verde.
InvShiftRows. Essa transformação muda as linhas da tabela (o quadrado do estado) para a direita (na direção oposta à mudança original). O valor do deslocamento para cada linha permanece o mesmo: a primeira linha (superior) não é deslocada c0 = 0, a segunda é deslocada por c1 = 1, a próxima é deslocada por c2 = 2 e a última é c3 = 3 posições (células). Os valores c0, c1, c2, c3 foram dados na tabela e na figura anterior para a primeira rodada de conversão de mensagens.

O resultado dessa multiplicação na representação escalar é:
S'0C = ({0l} S0C) {({0b} S1C) ⊕ ({0d} S2C) ⊕ ({09} S3C);
S'1C = ({09} S0C) ⊕ ({0l} S1C) ⊕ ({0b} S2C) ⊕ ({0d} S3C);
S'2C = ({0d} S0C) ⊕ ({09} S1C) ⊕ ({0l} S2C) ⊕ ({0b} S3C);
S'3C = ({0b} S0C) ⊕ ({0d} S1C) ⊕ ({09} S2C) ⊕ ({0l} S3C).
Para obter TI dos PCs, o algoritmo de descriptografia usa os mesmos valores de parâmetro que foram usados no processo de criptografia. Para a formação da chave expandida, as regras permanecem as mesmas.
Opção de descriptografia direta
As peculiaridades do algoritmo de descriptografia para algumas transformações inversas tornam possível preservar a mesma sequência de operações que no algoritmo de criptografia, mas alguns dos valores dos parâmetros requerem alterações. Primeiro de tudo, estamos falando sobre a chave (seu desdobramento).
A pesquisa mostrou que a ordem das funções SubBytes () e ShiftRows () não altera o valor do resultado, ou seja, essas funções são permutáveis (elas são comutadas). Esta posição (propriedade) também é verdadeira para as funções InvSubBytes (), InvShiftRows (). Esse padrão é fácil de explicar. O ponto é que ambas as funções operam em bytes inteiros, e os turnos são executados por um múltiplo inteiro de um byte e não alteram o valor dos próprios bytes.
Observe o seguinte sobre a operação MixColumns (). É linear para os bytes de entrada (dados).
InvMixColumns (chave redonda do estado XOR) = InvMixColumns (estado) XOR
InvMixColumns (chave redonda).
Esses recursos de funções (propriedades) permitem alterar a ordem do aplicativo, ou seja,
InvSubBytes (InvShiftRows ()) = InvShiftRows (InvSubBytes ()).
AddRoundKey (InvMixColumns ()) = InvMixColumns (AddRoundKey ()),
mas desde que as colunas (palavras de 32 bits) da chave de descriptografia expandida tenham sido passadas anteriormente pela função
InvMixColumns ().
O que precede significa que a maneira de descriptografar o PC pode ser efetivada preservando a ordem de uso das funções adotadas para criptografia. Obviamente, nesse caso, os custos de implementação de hardware e software da cifra são significativamente reduzidos. As alterações dizem respeito apenas ao procedimento para gerar a implementação da chave.
Na função InvMixColumns (), você precisa converter o tipo da variável, o parâmetro de entrada da função é uma matriz de bytes bidimensional (quadrado) e a chave expandida é formada como uma matriz linear (string) de palavras de 32 bits. Por esse motivo, é necessário executar a correspondência de tipos com o quadrado.
Vamos mostrar, usando o exemplo de uma transformação em duas etapas, duas versões equivalentes do procedimento de descriptografia RIJNDAEL. A primeira opção é o inverso usual da função de criptografia. A segunda opção é obtida a partir da primeira, alterando a ordem das operações em três pares de transformações
InvShi ftRows () → InvSubBytes () 2 vezes e
AddRoundKey () → InvMixColumns () 1 vezes.
O resultado da transformação é salvo ao passar da
sequência original para a inversa de operações nos pares especificados.
Na tabela, vemos que o procedimento de criptografia e a segunda variante do procedimento de descriptografia coincidem até a ordem do uso de chaves redondas (ao executar operações AddRoundKey), tabelas de substituição (ao executar operações SubBytes () e InvSubBytes ()) e matrizes de transformação (ao executar MixColumns ( ) e InvMixColumns ()).
Tabela 2 - Sequência de transformações na versão de duas rodadas do RIJNDAEL

Um resultado semelhante é verdadeiro para qualquer número de rodadas.
Recuperando uma Chave de Cifra Usando a Última Subchave
Geração de chaves de cifra redondas AES. A programação de teclas para gerar chaves redondas a partir de uma chave de cifra original de 128 bits é uma função recursiva. Esta função é discutida em detalhes aqui . As condições iniciais para o seu lançamento são as primeiras palavras de 4 bytes da chave (palavras de 4 × 32 bits), ou seja, W [0], W [1], W [2], W [3].
Vamos formular o problema de recuperar essa chave de cifra de 128 bits da seguinte maneira: Encontre os componentes da chave redonda redonda 10 [W], W [43], W [42], W [41], W [40].
É necessário recuperar a chave de cifra completa apenas com essa chave redonda.
É conveniente considerar a solução do problema primeiro em dados numéricos. Vamos tomar o exemplo numérico fornecido no FIPS PUB 197 como base.. A tabela 3 contém a tecla 10 redonda.
O procedimento para gerar chaves redondas é organizado de forma a fornecer movimento para frente (desdobramento da chave) ao longo de vários valores de chave anteriores. Para retroceder de algum ponto de uma série de valores, é necessário ter os dados iniciais do processo de computação nesse ponto de retorno. Seja o ponto de retorno o último passo da última 10ª rodada, ou seja, são conhecidas quatro palavras de 4 bytes da chave da 10ª rodada Nk = Nb = 4.
Tabela 3 - Chave de 128 bits da 10ª rodada da cifra AES

Além disso, os resultados e ações do algoritmo de recuperação de chave são colocados para conveniência na tabela 4, que é semelhante a uma (tipo de derrubada) tabela de geração de chaves.
Tabela 4 - Recuperação da chave de cifra da chave conhecida da 10ª rodada

Explicações para a Tabela 4. Os números das rodadas são contados na ordem inversa do dia 10 ao 1º. Três colunas (3, 8, 9) da tabela contêm teclas prontas com números atuais diferentes, dependendo do número da linha i. As células restantes contêm dados auxiliares para cálculos intermediários. Assim, o valor da chave W [i] aparece na tabela três vezes em três colunas.
As colunas 1 e 2 são o número r da rodada e o número ordinal i da palavra-chave de 4 bytes. A última palavra durante a criptografia tem o número i = 43. Na tabela, escrevemos na linha superior da coluna da direita (9). Os números de linha i da tabela estão diminuindo e na coluna 9 eles correspondem às palavras-chave W [i]. A oitava coluna contém a palavra W [i - Nk] da chave com um número reduzido W [43 - 4] = W [39] e a terceira coluna - a palavra-chave W [i - 1] = W [42], W anterior [i] = W [43].
O significado da palavra W [39] na 8ª coluna é desconhecido e o encontramos nos dados iniciais usando a fórmula:
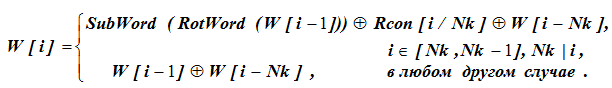
Para cálculos de fórmula, as condições para selecionar a linha da fórmula são primeiro verificadas. Para W [43], i = 43 e Nk não divide completamente o valor 43, ou seja, para i = 43, o valor de W [i] é determinado pela linha inferior da fórmula: W [43] = W [42] W [39]. Aqui, para os valores dados de W [42] e W [43], o último termo W [39] não está definido.
Então W [39] = W [43] W [42] = b6630ca6 - e13f0cc8.
Na aritmética binária mod2, as operações de adição e subtração são equivalentes, portanto, os cálculos bit a bit para cada um dos 4 bytes da palavra-chave W [39] assumem a forma (Tabela 5):
Tabela 5 - Cálculos em bytes da palavra-chave W [39].

Assim, o valor da palavra-chave W [39] = 575c006e foi encontrado. Transferimos esse valor para a 3ª coluna, para a linha i = 40 e para a 9ª coluna para a
linha i = 39. Os cálculos na linha i = 40 são realizados como ao expandir a chave.
A palavra desconhecida W [i - Nk] = W [40 –Nk] = W [i = 36] deve ser determinada como no caso anterior pela diferença W [36] = W [40] 7 coluna da linha 40.
Por sua vez, o valor em 7 A quinta coluna da linha 40 é formada como a soma (OR) da 5ª e 6ª colunas. O valor da 5ª coluna é obtido de W [39] após um turno cíclico do RotWord (4ª coluna) e uma operação de substituição de SubWord (5ª coluna).
Os resultados dessas ações assumem a forma
RotWord (575c006e) = 5c006e57; SubWord (5c006e57) = 4a639f5b.
O valor na 6ª coluna é obtido como uma constante
Rcon [j = i / Nk] = Rcon [j = 40/4] = 2 j-1 = 2 9 .
Essa constante é representada por um byte hexadecimal
2 9 ≈100000000 = x 9 , mas não existe esse byte no campo GF (2 8 ): você precisa encontrar o restante da divisão por um polinômio irredutível, ou seja,
Após incluir a constante na palavra-chave, temos Rcon [j = 40 / Nk] = 36000000 (6 coluna). O valor da 7a coluna é obtido como (7a coluna) = (5a coluna) ⊕ (6a coluna) = 4a639f5b⊕36000000 = 7c639f5b. E, finalmente, para W [36] = W [40] (7ª coluna da linha 40) = d014f9a8 7c639f5b = ac7766f3.
Cálculos adicionais por analogia levam ao resultado final - a tecla de cifra.
Há mais informações sobre as funções w e RotWord, Rcon e SubWord. Suponha que denotemos por Kr [j] - o j-ésimo byte da r-ésima chave redonda e w [i] como na documentação.
Nós obtemos: Kr = (w [Nk] r], w [Nk + r + 1], · · ·, w [Nk ∙ r + Nk - 1]).
Para diferentes i, temos as seguintes relações
para i ≠ 0 mod Nk, Nk ≤ i <Nb ∙ (Nr +1), w [i] = w [i - Nk] xor w [i - 1] e
para i = 0 mod Nk , w [i] = w [i-Nk] xou SubWord (Palavra-chave (w [i-1])) xorRcon [i / Nk].
Portanto, para i ≠ 0modNk, Nk 0≤i <Nb ∙ (Nr + 1) –Nk, w [i] = w [i + Nk] xor w [i + Nk - 1] e para i = 0modNk, w [i] = w [i + Nk] xorSubWord (Palavra-chave (w [i + Nk - 1])) xorRcon [i + Nk / Nk]
Com o AES-256, você precisa adicionar uma operação Subword quando i for comparável ao 4mod Nk. Portanto, é possível deduzir a chave anterior da subchave final e obter passo a passo o valor K0 da chave de cifra.
Os fundamentos matemáticos da cifra AES-128 são bastante completos e detalhados aqui .
Vamos voltar ao mapeamento de campo ℓ: GF (2 8 ) → GF (2 8 ); x → x 2 + x. A imagem desse mapeamento
1 = Im (l) tem dimensão dim GF (2) (1) = 7.
Equação x 2 + x = θ, onde θ1 tem duas soluções diferentes (raiz da equação) 1, 2є GF (2 8 ).
Pelo teorema Wyeth h1⊕h2 = 1, a soma das raízes é igual ao coeficiente da equação para x 2com o sinal oposto e o produto das raízes x1⊗x2 = θ é igual ao termo livre da equação (em nossa equação com o sinal oposto).
Sabe-se que na aritmética dos campos binários, as operações de adição e subtração dos elementos mod2 são equivalentes.

Assim, as raízes da equação são relacionadas pela razão x2 = x1⊕1, uma vez que o coeficiente em x na equação é 1. Isso significa que na representação decimal dos elementos de campo em sua ordem lexicográfica, eles estão localizados um após o outro, diferindo apenas um.
Portanto, para x = 0 ex = 1 e para x = 2 ex = 3, obtemos:

Os resultados (imagens) do mapeamento nos pares reduzidos (0, 1); (2, 3) coincidiu completamente, isto é, dois tipos correspondem a uma imagem. Consequentemente, a cardinalidade da imagem é duas vezes menor que a cardinalidade da pré-imagem e sua dimensão de seus elementos é 7.
O produto de pares de raízes, ou seja, o termo livre de uma equação quadrática é convenientemente definido através da representação de poder dos elementos do campo (imagens inversas). Neste caso, os expoentes são somados mod255, isto é, módulo a ordem do grupo multiplicativo do campo GF (2 8 ).