
Nascido para engatinhar não pode voar. Essa frase pode ser usada metaforicamente e literalmente, porque criaturas sem asas (ou partes funcionais do corpo) realmente não são capazes de conquistar os céus. Pelo menos a maioria deles. A regra não seria a regra se não houvesse exceções. No aspecto dos vôos sem asas, também há exceções - cobras de árvores decoradas ( Chrysopelea) Representantes desse tipo de cobra conseguem voar - uma habilidade extremamente útil, considerando que eles vivem nas copas das árvores acima do solo. Cientistas da Universidade Politécnica da Virgínia (EUA) decidiram considerar o vôo de uma cobra em termos de cinemática. Que características anatômicas permitem que as cobras voem (caem de maneira controlada, para ser exato), o que acontece durante o vôo em termos de cinemática e como essa pesquisa pode ajudar na robótica? As respostas para essas perguntas nos aguardam no relatório dos cientistas. Ir.
Base de estudo
Cobras de árvores decoradas são um gênero de serpentes encontradas no sul e no sudeste da Ásia. Representantes deste gênero não podem se orgulhar de grandes dimensões (comprimento do corpo apenas de 0,6 a 1,5 m) e veneno mortal. Embora as presas que caçam durante o dia não concordem com as últimas. Dado o habitat (copas das árvores), essas cobras têm muito poucos inimigos e, portanto, não precisam de um veneno forte. Além disso, eles têm táticas muito mais eficazes - sabem planejar.

As cobras voadoras, como são conhecidas popularmente, rastejam pelas árvores usando escamas duras ao longo da barriga, permitindo que se movam verticalmente. Se a cobra quiser se deslocar de uma árvore para outra, primeiro rasteja até a borda do galho e depois dobra o corpo na forma da letra latina "J" para mirar (para determinar o ângulo desejado de "decolagem" e o local de pouso). Tendo dito “vamos lá”, a cobra empurra seu corpo para frente e para cima, puxando seu estômago e costelas salientes (para que seu corpo se torne mais plano e levemente côncavo). Durante a asa-delta, a cobra constantemente faz movimentos corporais serpentinos de um lado para o outro, o que lhe permite controlar o vôo e pousar suavemente.
Vista lateral de uma serpente voadora planando Chrysopelea paradisi.
Uma vantagem adicional do método de movimento tão incomum para as cobras é a impressionante economia de energia, porque o vôo é muito mais rápido (e mais seguro) do que o rastejamento lento de uma árvore para outra no chão. Somente a partir dessa breve descrição, fica claro que existem muitos elementos importantes na mecânica do voo da cobra; ângulo de decolagem, forma do corpo durante a decolagem e vôo, movimento do corpo em voo, etc.
O aspecto mais marcante, especialmente para os observadores, do vôo da cobra é o movimento ondulado do corpo. Essa técnica é usada por muitas criaturas do planeta para se mover em terra e água. Você não precisa ir muito longe, porque as próprias cobras o usam perfeitamente. Os cientistas observam que o movimento ondulado na terra e na água foi estudado muito bem, mas essas piruetas no ar ainda são um mistério.
Nas cobras de Chrysopelea , a ondulação é caracterizada por uma forma do corpo em forma de S, uma baixa frequência de ondulação (1–2 Hz) e uma seção transversal aerodinâmica achatada do corpo.
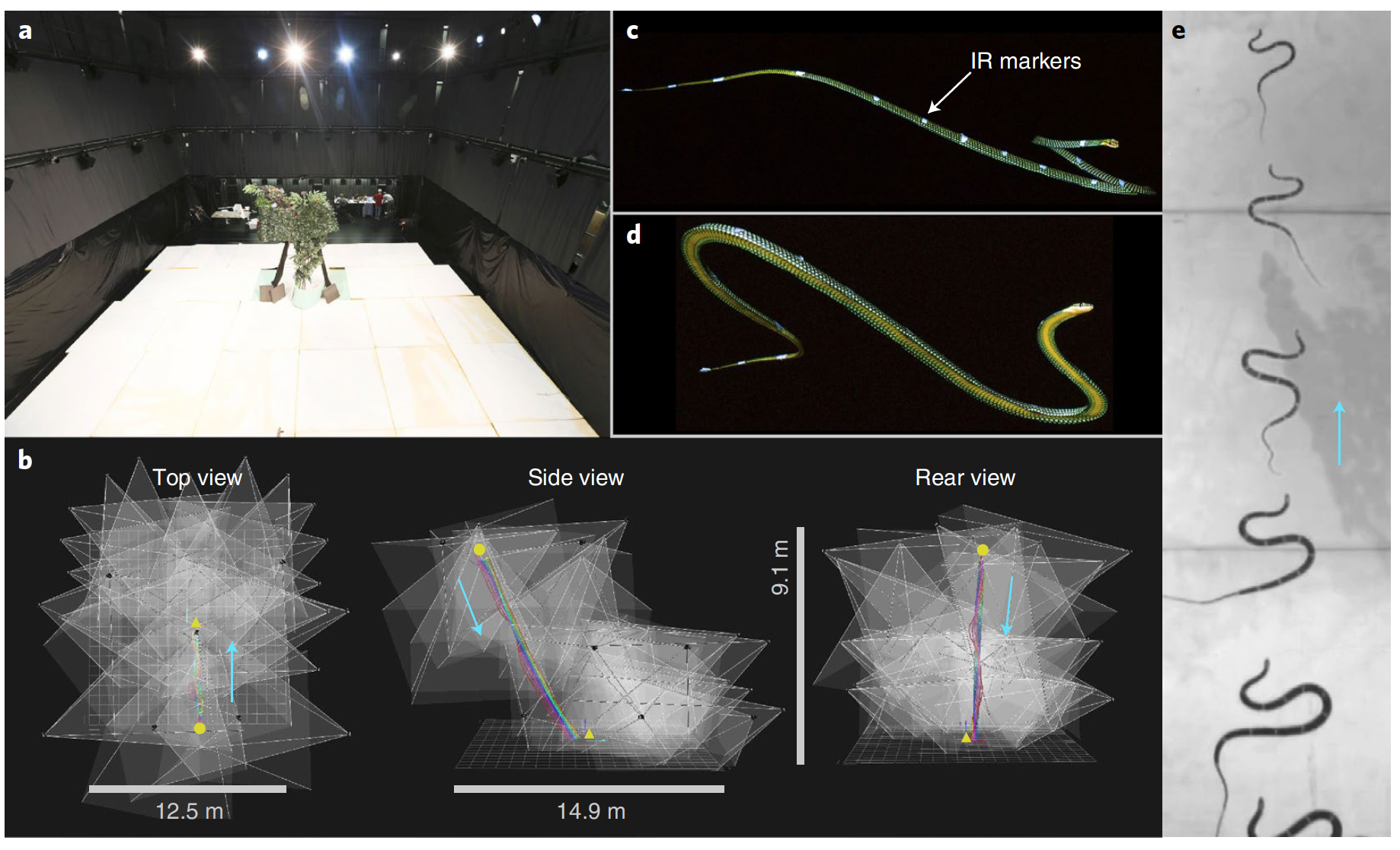
Imagem No. 1
De fato, a ondulação do ar reorganiza continuamente o corpo da cobra, transformando-o em uma forma de asa ( 1e) Estudos anteriores mostraram que as pipas sempre realizam movimentos ondulados em voo. No entanto, ainda não está claro se a ondulação é parte essencial de um voo bem-sucedido ou se é apenas um hábito. o aspecto comportamental do movimento em terra, migrou para o voo sem nenhuma intenção.
Se levarmos em conta a ondulação na terra e na água, podemos assumir que no ar isso gera impulso. Em meios sólidos, o movimento ondulado ocorre devido às forças de contato distribuídas sobre as regiões ventral e lateral do corpo e, na água, o deslocamento ou absorção de fluido ao longo do corpo causa movimento para frente. Nos dois casos, a força motriz líquida atua predominantemente no plano de ondulação. A modulação do corpo fora do plano (na direção vertical) pode ser usada para fins secundários, como diminuir a resistência ou aumentar a força normal.
Mas para empinar pipas, o planejamento bem-sucedido requer a geração de forças aerodinâmicas necessárias para compensar o peso do animal. As forças de sustentação e resistência são criadas pelo ar que flui através do corpo achatado quando é acelerado pela gravidade, e o movimento alternativo causado pelas contrações musculares provavelmente não aumenta a geração de força.
Vista frontal da decolagem e achatamento da cobra voadora Chrysopelea paradisi.
As forças aerodinâmicas resultantes devem agir fora do plano de ondulação, e a própria ondulação deve mudar constantemente a distribuição de forças no corpo da cobra. Também vale a pena considerar que as pipas podem "flutuar" não apenas na horizontal, mas na vertical. Isso significa que o modelo de voo de pipa contém elementos pitch * e roll * .
Inclinação * - movimento angular em relação ao eixo transversal horizontal de inércia.Neste estudo, os cientistas decidiram examinar mais de perto o papel da ondulação no voo de uma pipa. Usando imagens de alta velocidade do voo da cobra, os cientistas conseguiram quantificar as ondas de ar. Os dados obtidos nos permitiram criar um modelo tridimensional preciso do voo da cobra.
Rolar * - movimento angular em torno de seu eixo longitudinal.
Resultados da pesquisa
A ondulação do ar consiste em um conjunto de ondas de flexão horizontal e vertical. 11-17 marcadores foram colocados ao longo do corpo das cobras (7 indivíduos) participantes da pesquisa de vôo (a área de alta decolagem é de 8,3 m). A avaliação das alterações na posição desses marcadores permite determinar com precisão a estrutura da ondulação durante o voo.
Vista superior do planador de teste de uma cobra voadora Chrysopelea paradisi.
Marcadores infravermelhos obtidos durante o planejamento da pipa Chrysopelea paradisi.
Após 36 observações práticas, os cientistas criaram um modelo 3D do corpo da cobra ( r ).
Desenvolvimento de um modelo 3D de uma serpente voadora Chrysopelea paradisi baseada em dados de captura de movimento.
Usando o vetor tangente (t̂ = ∂r / ∂s), foi possível decompor a ondulação em duas ondas angulares que se movem ao longo do corpo.
As ondas horizontais e verticais são definidas pelas seguintes fórmulas:
θ̅ (s, t) = -tan -1 t̂ x / t y
e
ψ̅ (s, t) = sin -1 t̂ z
onde θ̅ (s, t) e ψ̅ (s, t ) São os ângulos locais que o corpo forma em relação às direções horizontal e vertical, em função do comprimento do arco se tempo t.
Os dados mostram que as pipas voadoras usam duas ondas: uma onda horizontal com uma grande amplitude e uma onda vertical com uma amplitude mais baixa, que passam sucessivamente pelo corpo da cabeça à cauda (imagem nº 2).

Imagem No. 2
Essas ondas se formam após o transitório inicial, quando a cobra salta em uma pose relativamente reta e depois forma uma pose característica em forma de S para o planejamento.
Existem quatro características da ondulação do ar que associam uma onda vertical à horizontal ( 2a ). Em primeiro lugar, uma onda vertical tem frequências espaciais e temporais duas vezes a frequência de uma onda horizontal. Isso indica que o corpo tem duas vezes mais dobras verticais do que as laterais ( 2a ,2f ). Segundo, as dobras em U no corpo de uma pipa voadora podem ser identificadas como cruzamentos zero no gráfico de ângulo de dobra ( 2b ). Terceiro, essas interseções são o máximo da onda vertical, indicando que as ondas horizontal e vertical estão 90 ° fora de fase. Quarto, a flexão fora do plano máxima ocorre nas curvas em U e aproximadamente a meio caminho ao longo dos segmentos retos. Nas curvas em U, a seção transversal da "asa" da cobra se dobra devido ao movimento do corpo fora do plano ( 1c , 1d ).
O formato das ondas viajantes muda com o tempo, à medida que a cobra acelera e produz forças aerodinâmicas, no entanto, algumas características ainda permanecem comuns. A onda horizontal é um sinusóide de topo plano cuja amplitude (80-120 °) depende do número de períodos espaciais, com menos períodos levando a ângulos de flexão horizontais mais altos. A onda vertical é um sinusóide de pico estreito, com amplos vales com amplitudes na faixa de 20 ° a 45 °.
Uma avaliação quantitativa das características espaciais e temporais das ondas mostrou que as cobras usam ondas horizontais com 1 a 1,5 períodos espaciais e uma frequência de onda de 1 a 1,7 Hz e ondas verticais com 2 a 3 períodos espaciais e uma frequência de onda de 2 a 3,4 Hz.
Há um componente adicional na ondulação do ar, que os cientistas chamam de "curva dorso-ventral", representando o movimento para cima e para baixo da parte de trás do corpo em relação à cabeça. O ângulo de inclinação desta dobra foi de -20 ° a 30 °. A curva dorso-ventral sempre esteve presente nos vôos observados, mas não teve relação significativa com o número de períodos espaciais.
Para determinar com precisão o grau de influência da relação entre as ondas horizontais e verticais, bem como a influência da flexão dorsoventral na dinâmica do voo, os cientistas criaram um modelo anatomicamente preciso de uma cobra em vôo. O controle sobre o modelo permite, segundo os cientistas, verificar sistematicamente como os componentes da ondulação (a amplitude da onda horizontal, o número de períodos espaciais e a frequência da ondulação) afetam a dinâmica do planejamento a curto e longo prazo.
A onda horizontal é modelada como um sinusóide com um pico plano de grande amplitude, e a onda vertical é modelada como um sinusóide de pequena amplitude:
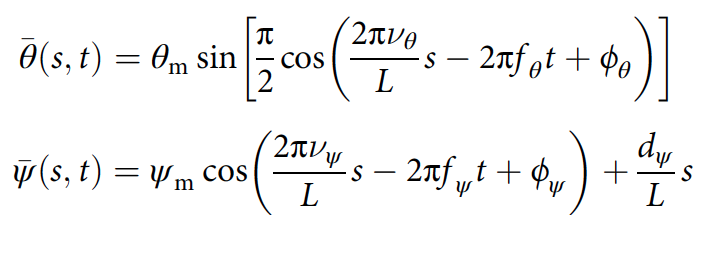
onde θ m e ψ m são os ângulos máximos de flexão horizontal e vertical; ν é o número de períodos espaciais; f é a frequência da ondulação; ϕ é a mudança de fase; d ψ - ângulo de flexão dorso-ventral; L é o comprimento do corpo ( 2f , 2g ).
Ondas horizontais e verticais são conectadas nos dados cinemáticos ( 2e ): ν ψ = 2ν θ , f ψ = 2f θ e ϕ ψ = 2 (ϕ θ- π / 2). Isso simplifica bastante o modelo para 5 variáveis que determinam a forma do corpo: θ m , ψ m , ν θ , f θ e d ψ .
A posição r = [x, y, z] do corpo em relação ao centro de massa é calculada da seguinte forma: x s x = cosψ̅sinθ̅, ∂ s y = -cosψ̅cosθ̅ e ∂ s z = sinψ̅.
A posição do centro de massa de R 0 e a orientação do corpo ( guinada * , pitch and roll ângulos ) são determinadas integrando as equações do movimento de translação e rotação.
Guinada * - movimentos angulares em torno do eixo vertical.
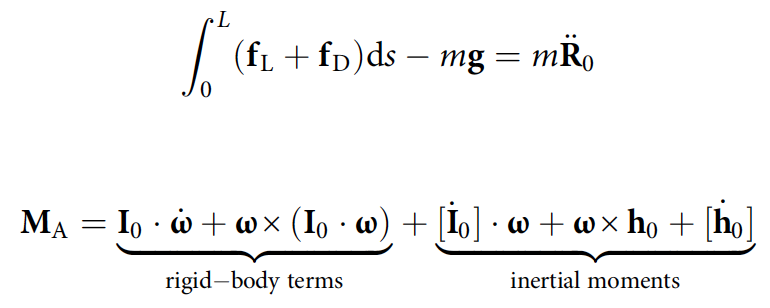
onde f G e F D são infinitesimais de elevação e de resistência forças; M A - momento aerodinâmico; m é a massa da cobra.
Para confirmar que o modelo matemático produz resultados fisicamente realistas, os cientistas simularam vôos usando parâmetros obtidos a partir de observações reais de planadores de pipas reais (a comparação de simulações e observações é mostrada na imagem abaixo).

Imagem No. 3
A julgar por comparação, o modelo funciona, mas possui algumas imprecisões menores que precisam ser abordadas no futuro.
Para verificar a influência da ondulação nas características do planejamento, foram realizadas duas simulações: com f θ = 0 Hz (sem ondulação) ef θ= 1,2 Hz (frequência média de ondulação nas cobras). Nos dois casos, ν θ e θ m foram variados ( 4a ).

Imagem No. 4 Os
dados cinemáticos da forma do corpo da cobra no modelo tornaram possível obter uma forma 121 com 1 ≤ ν θ ≤ 1,5 ondas corporais e amplitudes de ondas horizontais na faixa de 90 ° ≤ θ m ≤ 119 °. Além disso, as formas corporais observadas foram extraídas dessa matriz (parte do meio do gráfico, separada ao longo da diagonal; 4b ). A parte do gráfico abaixo destacada contém formas de corpo “abertas” (semelhantes à letra S) e a parte superior é “fechada” (semelhante a um sinal de infinito).
A amplitude da onda vertical e o ângulo dorsoventral foram mantidos em um nível constante: 20 ° e 10 °, respectivamente. A simulação foi considerada completa quando o centro de massa do corpo da cobra tocou o solo (aterrissagem) ou quando algum dos ângulos de orientação excedeu o valor limite de 85 °. Se isso acontecesse, o planejamento era considerado instável, ou seja, não é o mesmo que na natureza. Durante a simulação, foram testadas a dinâmica de curto prazo (altura inicial 10 m) e dinâmica de longo prazo (altura inicial 75 m) com / sem ondulação.
O modelo mostra que as ondulações têm um efeito positivo no desempenho de deslizamento, geralmente aumentando as distâncias horizontais e verticais percorridas antes que a pipa simulada se torne instável.
Simulação de uma cobra voadora planejando com ondulação e sem ela.
Planadores curtos com uma altura de lançamento de 10 m mostraram um bom coeficiente de estabilidade na presença de ondulação (94%). Se a ondulação não foi incluída no modelo, apenas 50% dos voos permaneceram estáveis. A ondulação também aumenta a distância de planejamento (de 4 ma 4,3 m).
Ao simular o deslize a partir de 75 m, a ondulação aumentou a distância horizontal e vertical antes que a instabilidade se manifestasse em 86% dos lançamentos. Nesse caso, a ondulação também aumentou a distância do vôo em 92% dos lançamentos. A ondulação também aumentou a distância horizontal média em 6,9 m.
Para esclarecer a influência da amplitude da onda vertical e da flexão dorsoventral na dinâmica do deslizamento, diferentes valores desses parâmetros foram utilizados na modelagem e os resultados foram considerados.
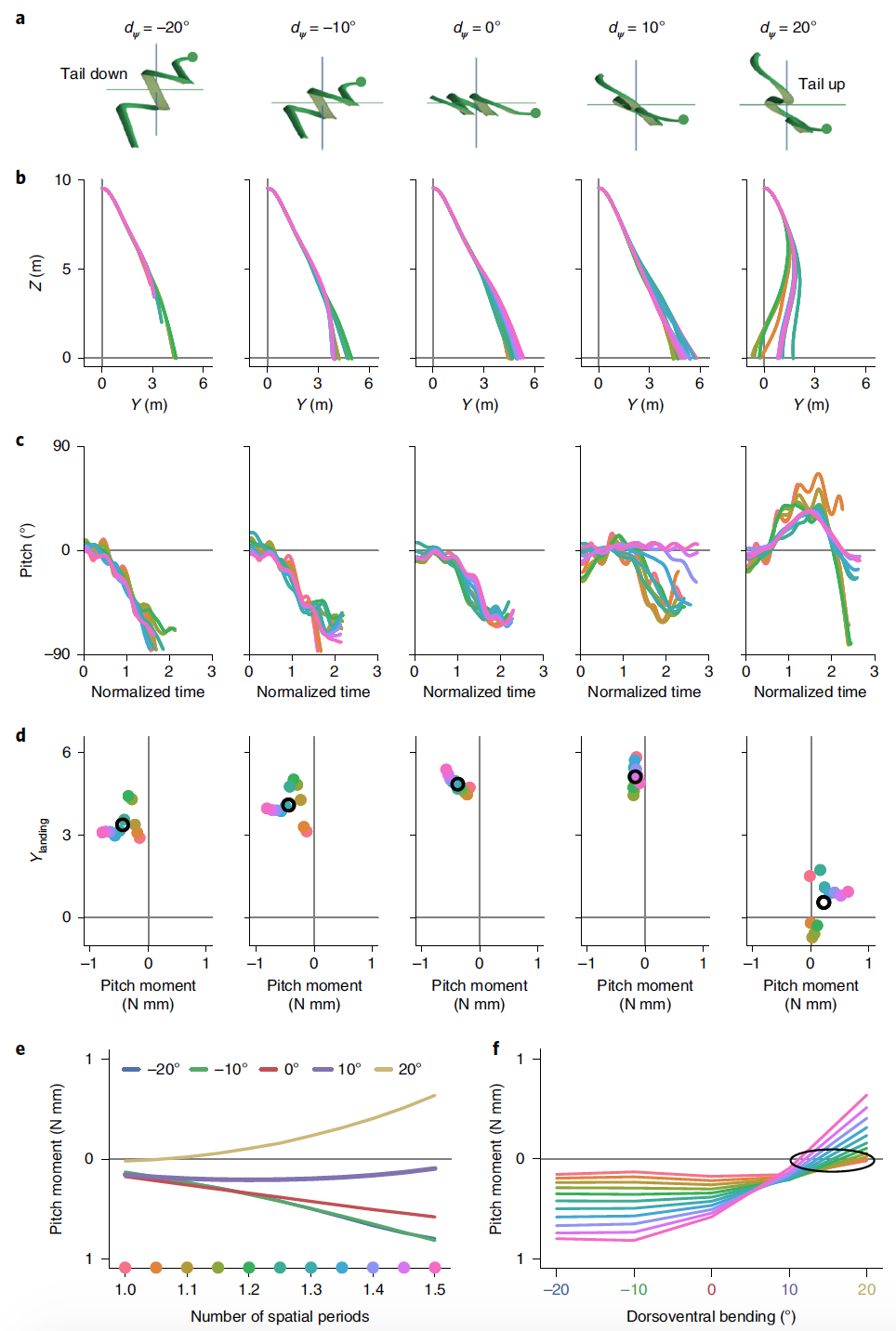
Imagem No. 5 O
planejamento foi modelado com ψ m = 0 °, 10 ° e 20 ° e uma curva dorsoventral de -20 ° a 20 ° em incrementos de 10 ° ( 5a ) para 11 formas corporais diferentes.
A oscilação vertical tem relativamente pouco efeito na trajetória de deslizamento, enquanto a curva dorsoventral tem um impacto significativo.
Uma cobra perfeitamente plana (ψ m= 0 °), que nunca foi observado durante testes experimentais, mostrou os piores resultados esperados. O aumento da amplitude da onda vertical aumentou a eficiência do planejamento devido à torção da seção transversal no plano, o que fornece um ângulo mais favorável para a criação da força ( 2j ).
Em contraste com a amplitude da onda vertical, a curva dorsoventral teve um efeito notável nas características do planejamento, especialmente no tom.
No ψ m = -20 ° com a parte de trás do corpo abaixo da cabeça, o deslizamento não era superficial, em vez disso, tornou-se instável na altura de queda até 10 m. No ψ m= 20 ° com a parte de trás do corpo acima da cabeça, a trajetória é curvada para trás, com algumas formas do corpo pousando atrás do salto. Um planejamento tão ruim é justificado por uma inclinação ascendente do corpo. No entanto, planadores com os parâmetros acima apresentaram boa estabilidade rotacional.
Simulações não rotativas foram realizadas para testar a relação entre o desempenho da flexão do corpo dorsoventral, rotação e deslizamento. Em vez de resolver um sistema não linear acoplado das equações # 4 e # 5, os cientistas amostraram as forças aerodinâmicas em diferentes fases do corpo durante o ciclo de ondulação. Em seguida, a equação nº 4 foi integrada aqui, e a posição e a velocidade do centro de massa foram calculadas.
Em essência, essa manipulação é um experimento de "túnel de vento virtual", no qual um modelo dinâmico é usado para calcular as forças distribuídas que agem sobre um corpo à medida que acelera. Este método permite eliminar a relação entre movimento de translação e rotação, a fim de quantificar contribuições aerodinâmicas e inerciais individuais ao movimento de rotação.
Com um aumento na curva dorsoventral de -20 ° a 10 °, a posição de aterrissagem da cobra simulada aumenta à medida que o tom médio aumenta na direção zero ( 5d ). Em uma curva dorsoventral de 20 °, o momento da inclinação média da fase se torna positivo e o desempenho de deslizamento diminui.
Para cada ângulo de flexão dorsoventral, a eficiência do planejamento e o momento oblíquo médio também dependem da forma utilizada, em particular do número de períodos espaciais e da amplitude da onda horizontal. Para qualquer formato do corpo no momento do planejamento, a curva dorsoventral tem um grande efeito no momento médio do arremesso e, com um aumento no número de períodos espaciais, os momentos divergem, tornando-se mais positivos ou negativos, dependendo de d ψ .
As marcações dos momentos médios da fase em 5e correspondem à inclinação ascendente ou inclinação mostrada em 5c e o desempenho resultante de deslizamento em 5b . Às 5fé mostrado que, para as formas do corpo com o menor período espacial, o momento médio de inclinação será o menor.
A partir dos dados acima, pode-se supor que a onda vertical faz com que o corpo se enrole para fora do avião, alterando a orientação local da "asa achatada" (a forma do corpo da cobra durante o planejamento) usando um fluxo de ar. A curva dorsoventral controla a magnitude e o sinal do momento aerodinâmico que afeta o corpo. Uma pipa voadora pode controlar o momento do lançamento alterando o ângulo de curvatura dorsoventral ou a forma de onda horizontal durante o vôo.
Consequentemente, a curvatura dorsoventral do corpo desempenha um papel extremamente importante na estabilidade do planador, no pouso bem-sucedido e na capacidade de alterar a trajetória do planador durante a execução.

Imagem Nº 6
A análise de fases por média permite quantificar a contribuição relativa de momentos aerodinâmicos e inerciais para a dinâmica de deslizamento.
As equações 5 implicam que a orientação do corpo é influenciada pelas forças aerodinâmicas e pela mudança na distribuição de massa. A contribuição aerodinâmica ( 6a ) aumenta com o tempo à medida que a velocidade aumenta, enquanto a contribuição inercial ( 6b ) permanece constante. Ambos os momentos são periódicos e apenas o momento do pitch mostra uma média de fase diferente de zero.
Inicialmente, os momentos de inércia predominam perto dos eixos de inclinação e rotação, mas durante um ciclo de onda, sua contribuição diminui rapidamente. Os momentos inerciais de guinada, em regra, são uma ordem de magnitude maior que os momentos aerodinâmicos de guinada e são maiores que os momentos inerciais em torno de outros eixos. Momentos inerciais de guinada surgem devido a uma onda horizontal de grande amplitude e a um amplo corpo em forma de S. Este resultado sugere que as pipas voadoras podem usar a rotação inercial como mecanismo de manobra.
Para um conhecimento mais detalhado das nuances do estudo, recomendo que você analise o relatório dos cientistas e materiais adicionais .
E aqueles que desejam se familiarizar com o software usado para analisar o planejamento de uma pipa voadora podem seguir este link .
Epílogo
Neste estudo, os pesquisadores usaram as mais recentes técnicas de captura de movimento e modelagem 3D para criar um modelo anatomicamente preciso de uma cobra voadora.
Compreender a dinâmica do voo de um pássaro já foi difícil, mas não confundiu os cientistas tanto quanto uma pipa. Na natureza, não existem muitos exemplos de vôos sem asas, e todos eles estão associados ao uso de mecanismos não padronizados que permitem ao animal planejar, e não cair como uma pedra no chão.
No caso de cobras voadoras, a ondulação observada no movimento das cobras rastejantes e flutuantes desempenha um papel muito importante. Um mecanismo adicional para a estabilização do planejamento é a correção do ângulo dorsoventral de flexão do corpo. Ao combinar esses elementos, as pipas voam de árvore em árvore, sabendo exatamente o local do plantio futuro.
Os autores deste trabalho acreditam que seus dados não apenas nos permitiram entender melhor os hábitos das cobras de árvores decoradas, mas também para obter inspiração adicional para a criação de robôs semelhantes a cobras. Sim, já existem esses robôs. Eles rastejam, podem navegar por superfícies difíceis e chegar a lugares de difícil acesso, mas podem voar?
Com esse raciocínio, em breve o mundo se parecerá com a cidade de máquinas da "Matrix", onde criaturas robóticas extremamente incomuns (e um pouco assustadoras) se arrastam pelas paredes, cujo objetivo era difícil de entender. O desejo de uma pessoa de fazer uma versão robótica de tudo o que a rodeia não pode ser enganado. Essa é a nossa natureza - entender tudo, saber tudo, ser capaz de criar o que a natureza fez lindamente diante de nós. Se houver muito mais benefícios do que danos causados por cobras, aranhas, cães e outros animais robóticos, essa pesquisa é totalmente justificada.
Obrigado por assistir, fique curioso e tenha um ótimo final de semana a todos, pessoal!
Sexta-feira off-top:
, .
, .
Fora da parte superior 2.0:
, :)
, :)
Um pouco de publicidade
Obrigado por ficar com a gente. Você gosta dos nossos artigos? Deseja ver materiais mais interessantes? Ajude-nos fazendo um pedido ou recomendando aos amigos o VPS na nuvem para desenvolvedores a partir de US $ 4,99 , um análogo exclusivo de servidores de nível básico que inventamos para você: Toda a verdade sobre o VPS (KVM) E5-2697 v3 (6 núcleos) 10 GB DDR4 480 GB SSD 1 Gbps de US $ 19 ou como dividir o servidor? (as opções estão disponíveis com RAID1 e RAID10, até 24 núcleos e até 40GB DDR4).
Dell R730xd 2 vezes mais barato no data center Equinix Tier IV em Amsterdã? Apenas temos 2 TVs Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 TV a partir de US $ 199 na Holanda!Dell R420 - 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB - a partir de US $ 99! Leia sobre Como construir a infraestrutura do bldg. classe usando servidores Dell R730xd E5-2650 v4 que custam 9.000 euros por centavo?