Clever Geek Handbook

Projeto Tutorial do Python: Algoritmo de Dijkstra, OpenCV e UI (Parte 1)

Labirintos são um quebra-cabeça comum para seres humanos, mas são um problema de programação interessante que podemos resolver usando métodos de caminho mais curto, como o algoritmo de Dijkstra.



Lembrando o algoritmo de Dijkstra



O algoritmo de Dijkstra é um dos algoritmos mais populares da teoria dos grafos. É usado para encontrar o caminho mais curto entre os nós em um gráfico direcionado. Começaremos com o nó original e os comprimentos de borda conhecidos entre os nós.



Primeiro, atribuímos a distância da fonte a todos os nós. O nó s obtém o valor 0 porque é a fonte; o resto obtém valores to para começar.



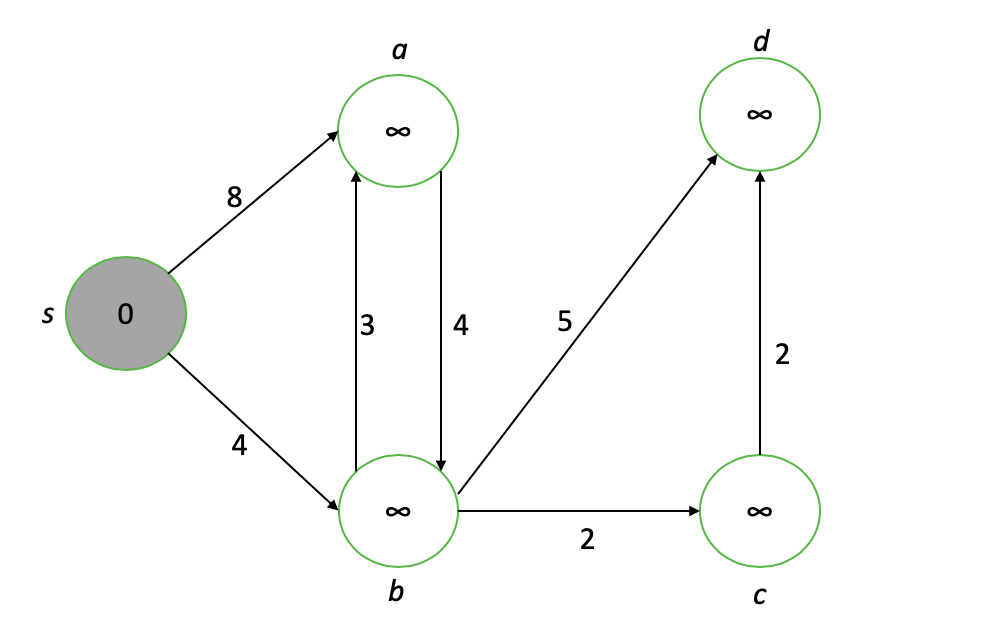
imagem



Nosso nó de interesse é o nó bruto com o valor mais baixo (mostrado em cinza), ou seja, s. Primeiro, "enfraquecemos" cada vértice adjacente ao nosso nó de interesse, atualizando seus valores para o mínimo de seu valor atual ou o valor do nó de interesse mais o comprimento da borda de conexão ...



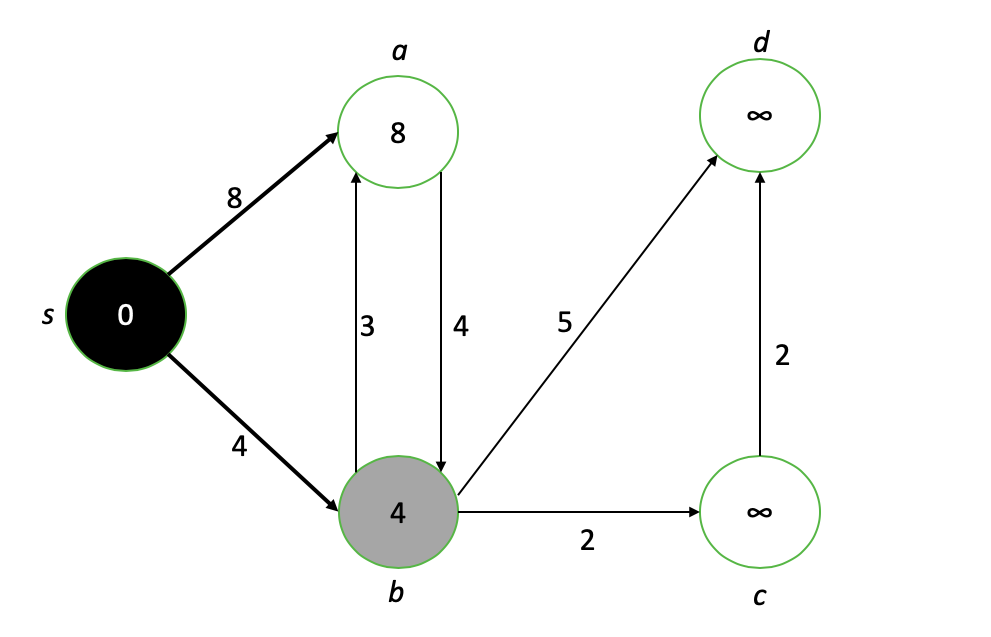
imagem



O nó s agora está completo (preto) e seus vizinhos a e b assumiram novos valores. Como o novo nó de interesse é b, repetimos o processo de "enfraquecer" os nós vizinhos de be finalizamos o valor do caminho mais curto para b.



imagem



Depois de percorrer cada nó, terminamos com um gráfico que mostra o menor comprimento do caminho da origem para cada nó.



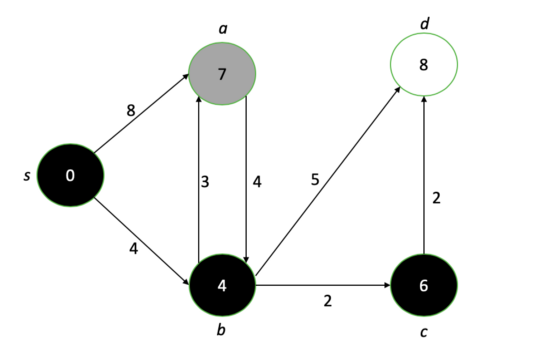
imagem



imagem



imagem



Nosso diagrama final depois de executar o algoritmo de Dijkstra. Os números em cada nó representam a menor distância possível do nó de origem.



Conceitualizando imagens de labirinto



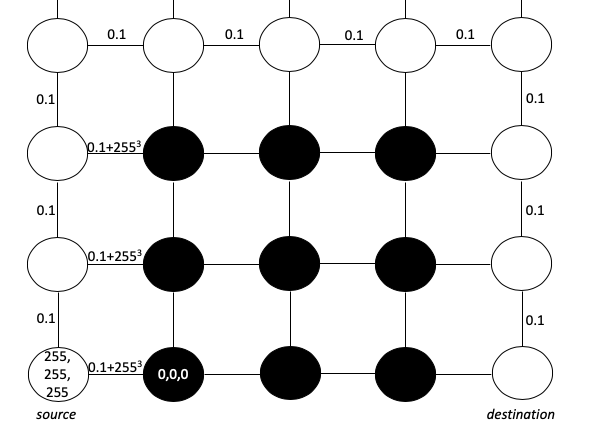
imagem



Podemos pensar em uma imagem como uma matriz de pixels. Cada pixel (por simplicidade) tem um valor RGB de 0,0,0 (preto) ou 255.255.255 (branco). Nosso objetivo é criar um caminho mais curto que comece em branco e não ultrapasse as bordas pretas. Para representar esse objetivo, podemos tratar cada pixel como um nó e desenhar arestas entre pixels adjacentes com comprimentos de arestas com base na diferença nos valores RGB. Usaremos a fórmula da distância quadrada euclidiana e adicionaremos 0,1 para garantir que não haja comprimento do caminho 0 - (requisito para o algoritmo de Dijkstra):



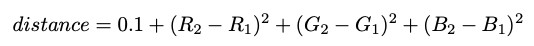
imagem



Essa fórmula torna a distância de interseção ao longo do limite do labirinto excessivamente grande. Como podemos ver, o caminho mais curto da origem ao destino passará claramente pela barreira e não através dela.



imagem



Implementação



Podemos usar o OpenCV, uma popular biblioteca de visão computacional para Python, para extrair valores de pixels e exibir nossas imagens de labirinto. Vamos também definir as coordenadas de nossas localizações inicial e final, adicionando pontos ao nosso labirinto 



import cv2
import matplotlib.pyplot as plt
import numpy as np
img = cv2.imread('maze.png') # read an image from a file using
cv2.circle(img,(5,220), 3, (255,0,0), -1) # add a circle at (5, 220)
cv2.circle(img, (25,5), 3, (0,0,255), -1) # add a circle at (5,5)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image
plt.show()


imagem


Estamos criando uma classe Vertex que nos ajudará a rastrear as coordenadas. Também queremos rastrear o nó pai para que possamos restaurar o caminho inteiro assim que encontrarmos os valores de distância. 



class Vertex:
    def __init__(self,x_coord,y_coord):
        self.x=x_coord
        self.y=y_coord
        self.d=float('inf') #current distance from source node
        self.parent_x=None
        self.parent_y=None
        self.processed=False
        self.index_in_queue=None


Precisamos criar uma matriz de vértices representando o arranjo bidimensional de pixels na imagem. Essa será a base do algoritmo de Dijkstra. Também mantemos uma fila com um monte mínimo de prioridades para o rastreamento de nós brutos. 



def find_shortest_path(img,src,dst):
    pq=[] #min-heap priority queue
    imagerows,imagecols=img.shape[0],img.shape[1]
    matrix = np.full((imagerows, imagecols), None) 
    #access matrix elements by matrix[row][col]
    #fill matrix with vertices
    for r in range(imagerows):
        for c in range(imagecols):
            matrix[r][c]=Vertex(c,r)
            matrix[r][c].index_in_queue=len(pq)
            pq.append(matrix[r][c])
    #set source distance value to 0
    matrix[source_y][source_x].d=0
    #maintain min-heap invariant (minimum d Vertex at list index 0)
    pq = bubble_up(pq, matrix[source_y][source_x].index_in_queue)


Precisamos de algumas funções auxiliares para nos ajudar a encontrar arestas e o comprimento das arestas entre os vértices: 



#Implement euclidean squared distance formula
def get_distance(img,u,v):
    return 0.1 + (float(img[v][0])-float(img[u][0]))**2+(float(img[v][1])-float(img[u][1]))**2+(float(img[v][2])-float(img[u][2]))**2
#Return neighbor directly above, below, right, and left
def get_neighbors(mat,r,c):
    shape=mat.shape
    neighbors=[]
    #ensure neighbors are within image boundaries
    if r > 0 and not mat[r-1][c].processed:
         neighbors.append(mat[r-1][c])
    if r < shape[0] - 1 and not mat[r+1][c].processed:
            neighbors.append(mat[r+1][c])
    if c > 0 and not mat[r][c-1].processed:
        neighbors.append(mat[r][c-1])
    if c < shape[1] - 1 and not mat[r][c+1].processed:
            neighbors.append(mat[r][c+1])
    return neighbors


Agora podemos implementar o algoritmo de Dijkstra e atribuir valores de distância (d) a todos os vértices de pixels na imagem do labirinto: 



while len(pq) > 0:
    u=pq[0] #smallest-value unprocessed node
    #remove node of interest from the queue
    pq[0]=pq[-1] 
    pq[0].index_in_queue=0
    pq.pop()
    pq=bubble_down(pq,0) #min-heap function, see source code 
    
    u.processed=True
    neighbors = get_neighbors(matrix,u.y,u.x)
    for v in neighbors:
        dist=get_distance(img,(u.y,u.x),(v.y,v.x))
        if u.d + dist < v.d:
            v.d = u.d+dist
            v.parent_x=u.x #keep track of the shortest path
            v.parent_y=u.y
            idx=v.index_in_queue
            pq=bubble_down(pq,idx) 
            pq=bubble_up(pq,idx)


Agora podemos chamar a função de caminho mais curto e desenhar a solução em nosso labirinto: 



img = cv2.imread('maze.png') # read an image from a file using opencv (cv2) library
p = find_shortest_path(img, (25,5), (5,220))
drawPath(img,p)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image on the screen 
plt.show()


imagem



imagem



Vamos tentar outros labirintos de toda a internet.



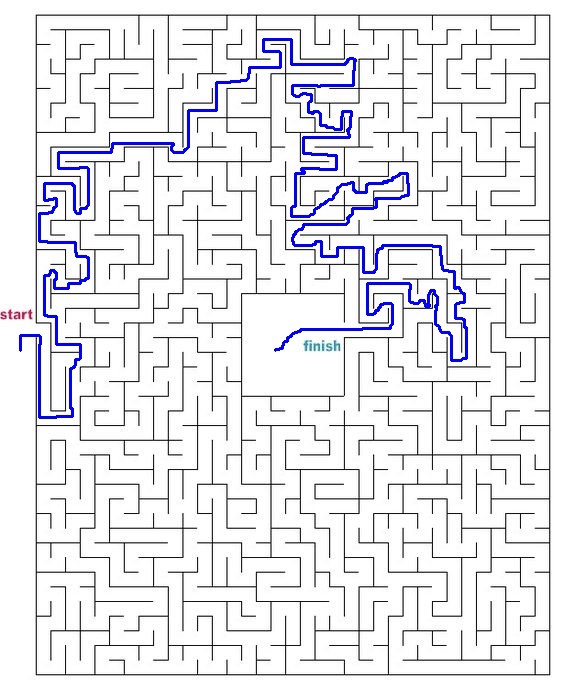
imagem



imagem



imagem



imagem



O código fonte completo está disponível no GitHub aqui .



Continuação: Projeto de Aprendizagem em Python: Interface de 40 linhas de código (parte 2)



imagem



Aprenda os detalhes de como obter uma profissão de alto nível do zero ou subir de nível em habilidades e salários fazendo nossos cursos online pagos SkillFactory:










More articles:


All Articles