
Outros artigos do ciclo
O motivo da publicação de textos detalhados sobre o padrão AES é o fornecimento da oportunidade de se familiarizar com ele em detalhes suficientes não apenas para desenvolver uma implementação de software independente do algoritmo de criptografia, mas também para criar algoritmos para possíveis ataques criptoanalíticos na cifra, ou seja, para descriptografar as cifras sem conhecer a chave ...
As publicações disponíveis na rede não atendem a esses objetivos e não podem ser usadas por mim no processo de treinamento de especialistas.
Um dos principais requisitos antigos (ou mesmo antigos) das cifras é criar um algoritmo de criptografia e criptografia aberto (acessível para estudo) em torno dele (modos, protocolos etc.), exceto a chave de cifra. A chave é algo que deve ser mantido na mais estrita confiança de todos. Nesse caso, a chave não precisa ser classificada como "Segredo". O limite de tal condição é que apenas o destinatário do cifragram possui a chave, ele próprio, em princípio, deve estabelecê-la.
Para sistemas de criptografia simétrica, essa condição não é viável. E essa é a diferença fundamental entre sistemas assimétricos (duas chaves) e sistemas simétricos, nos quais a fonte do vazamento de informações importantes pode não ser a única. Foi observado anteriormente que o AES é uma versão simplificada da cifra RIJNDAEL, e aqui usaremos a versão completa em alguns locais.
AES (Key Schedule).
Escolher uma chave ao criptografar uma mensagem é uma tarefa responsável. A abordagem geral é que um vetor binário aleatório é selecionado e usado para a chave em um espaço vetorial multidimensional. Freqüentemente, vários algoritmos de criptografia e cifras são caracterizados pela presença de chaves fracas ou inválidas, identificadas durante o desenvolvimento das cifras ou durante sua operação durante pesquisas adicionais algoritmos de autores ou analistas de criptografia e, consequentemente, publicações sobre o assunto.
Por sua vez, isso impõe restrições ao procedimento de geração de chaves, o que é indesejável, pois o complica. Os fundamentos matemáticos para criptografia são muito semelhantes aos fundamentos matemáticos para gerar chaves, e você pode ler sobre eles em detalhes aqui .
O vetor binário selecionado é chamado de chave de cifra e é convertido em um "quadrado" de 4 × 4 = 16 bytes. Em seguida, as chaves redondas são formadas a partir dele usando dois procedimentos especiais, que são usados nos processos de criptografia / descriptografia, descritos em detalhes aqui .
Um procedimento é chamado de expansão de chave, o outro é chamado de seleção de chave redonda. O vetor aleatório aleatório selecionado com um comprimento fixo é expandido. Também é importante considerar cuidadosamente a escolha de um sensor de número aleatório, realizar seus testes e testes.
Expansão chave
O significado de expandir a chave original (selecionada) consiste em dividi-la em blocos (32 bits cada) e depois gerar a partir deles um conjunto de novos blocos do mesmo comprimento para cada rodada.
Portanto, selecione a chave de cifra (128 bits) AES = 2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 cf 4f 3c, para Nk = 4, que é representado por blocos de 4 bytes e sua extensão redonda inicial tem a forma w [0 ] = 2b7e1516; w [1] = 28aed2a6; w [2] = abf71588; w [3] = 09cf4f3c. O símbolo w [i] na tabela CQ, i = 0 (1) 43, indica uma coluna de 4 bytes da chave redonda.
Uma sessão de criptografia é a preparação e transformação algorítmica de uma mensagem, como uma carta. O texto da letra na representação de bits é dividido em blocos de comprimento fixo Nb = 128, 192 ou 256 bits. No AES, o comprimento do bloco é de apenas 128 bits.
Então cada bloco é representado por um quadrado ou (retângulo com 4 linhas) e é criptografado separadamente para um número fixo de rodadas Nr = Nr (Nb, Nk), que é uma função de duas variáveis: o comprimento do bloco Nb e o comprimento da chave Nk, que pode assumir valores independentemente 128, 192, 256 bits.
A escolha da chave de criptografia não impõe restrições à própria sequência de bits. Cada uma das rodadas Nr usa sua própria chave redonda pré-formada ou calculada diretamente, {w [i]}.
As chaves redondas são formadas a partir da chave de criptografia usando um algoritmo especial, que inclui o procedimento de expansão de chave e o procedimento de seleção de chave redonda. Especificar chaves redondas diretamente, ignorando esses procedimentos, é inaceitável.
A essência e o objetivo do primeiro procedimento é converter uma determinada chave de criptografia original em uma chave mais longa e expandida (Chave Expandida). O número total de bits da chave estendida a partir da qual as chaves redondas são selecionadas é determinado pelo produto K = Nk (Nr + 1) - o número de bits do bloco de chaves é multiplicado pelo número de voltas aumentadas em um.
Exemplo 1 . Seja Nb = Nk = 4, dados blocos de comprimento 4 × 32 = 128 bits, depois Nr = 10.
Comprimento K em bits para a chave estendida K = 128 ∙ 11 = 1408 bits.
O segundo procedimento (Seleção de Teclas Redondas) é uma seleção seqüencial de 32Nk, ou seja, 4 palavras de 32 bits da chave estendida, ou seja, a primeira tecla de círculo é representada pelas palavras Nk iniciais recém-formadas, a segunda tecla de arredondamento pelas seguintes palavras Nk e assim por diante até a última rodada.
Exemplo 2. Com os mesmos dados iniciais (veja o exemplo anterior), o comprimento total da chave estendida em bytes contém Nk (Nr + 1) = 4 ∙ 11 = 44 palavras de quatro bytes W (i),
i = 0 (1) Nk (Nr + 1) - 1 As linhas da tabela CQ são numeradas por números naturais. A primeira linha possui o número 4, pois 4 linhas (com números 0,1,2,3) com uma chave de cifra não estão incluídas na tabela CQ.
Chave de cifra de mesa AES para todas as 10 rodadas (consulte a tabela QC abaixo).
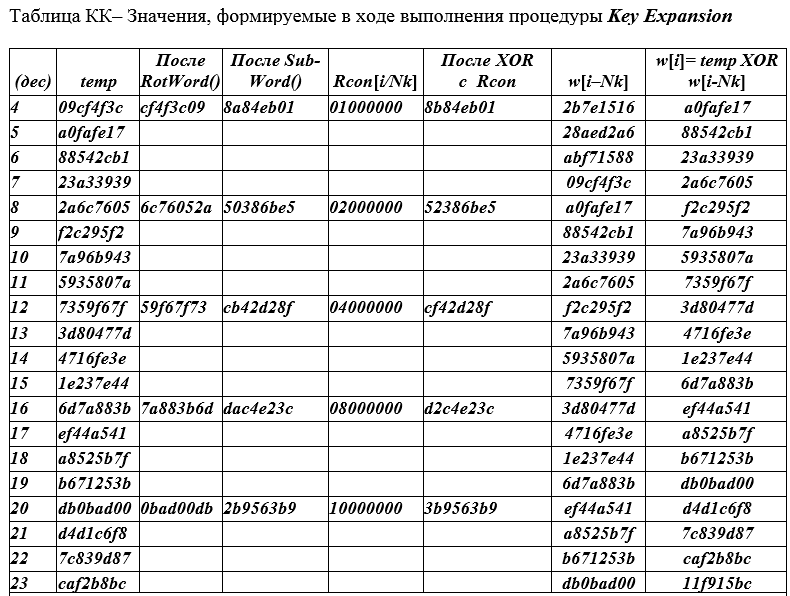
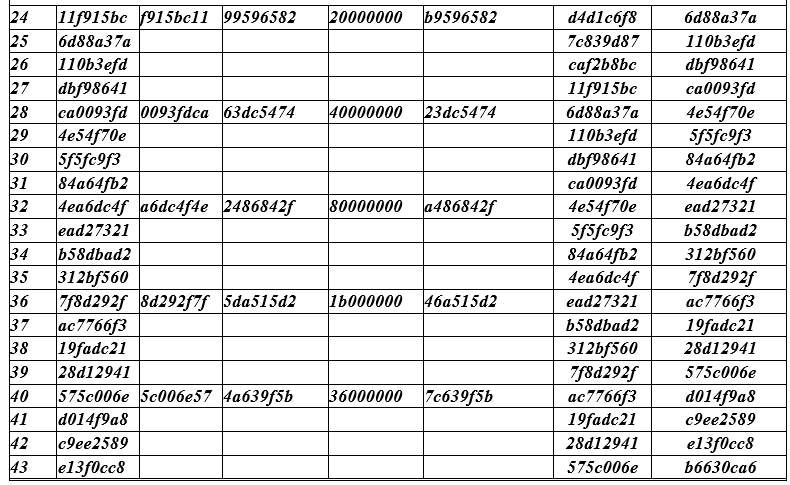
As linhas da tabela são divididas em grupos (4 linhas cada). Em cada grupo, apenas uma linha superior é preenchida em todos os campos. Nas próximas três linhas, apenas os campos extremos (esquerda e direita) são preenchidos. Os valores obtidos da margem direita da linha acima dela são inseridos na margem esquerda ( temp ) da próxima e nas duas linhas subsequentes.
Damos um exemplo de preenchimento da primeira linha com o número i = 4 da tabela CQ. Coluna esquerda - os números de linha atuais começam com o valor (4), pois os primeiros 0,1,2,3 valores não estão incluídos na tabela. Em geral, o índice (número da linha) i é executado sobre os valores i = 0 (1) Nk (Nr + 1) -1 ou i = 0 (1) 43 no total de 44 palavras de 32 bits.
Para a coluna tempo valor w [i-1] = 09cf4f3c é colocado e por rotação (mudança cíclica de um byte) RotWord () obtemos o valor CF4F3C09, que é colocado na coluna 3. A quarta coluna contém o resultado de 8A84EB01, substituindo bytes de SubBytes dos valores da terceira coluna , isto é, CF → 8A; 4F → 84; 3C → EB; 09 → 01 => 8A84EV01.
Cada quarta linha da tabela na 5ª coluna é preenchida com o valor Rcon [i / Nk], uma constante calculada pela fórmula Rcon (J) = 01000000, j = [i / Nk] = 2 j-1 = 2 0 = 1) o valor 01 00 00 00 é escrito com palavras de 4 bytes, o primeiro byte é 2 0 = 1, ou seja, 0000 0001 2 , os bytes restantes desta palavra de 32 bits são zero.
O campo da coluna 6 contém a soma (XOR) dos campos do 4º e 5º 884EB01 + 01000000 = 8B84EB01;
O campo da coluna 7 contém W [i - Nk] = W [4-4] = W [0] = 2B7E1516;
O campo Coluna 8 contém a soma dos campos das colunas 6 e 7 W [i = 4] = 884EB01 + 2B7E1516 = A0FAFE17;
E agora em detalhes e com detalhes, consideraremos os procedimentos nomeados.
Procedimento de expansão de chave
Vamos considerar em detalhes o procedimento para gerar uma Chave Expandida a partir da chave de cifra original. Formalmente, a chave estendida W será descrita por uma sequência de blocos W [i], i = 0 (1) Nk (Nr + 1) -1, palavras de 4 bytes (teclas redondas) contidas na última coluna da tabela KK, na qual a primeira Nk de 32 bits palavras representam a chave original, isto é,
W = {W [0], W [1], W [2], W [3], W [4], ..., W [K-1]}
subsequente i- ésimo as palavras são formadas recursivamente a partir de palavras anteriores, de acordo com uma expressão na qual a soma é XOR.
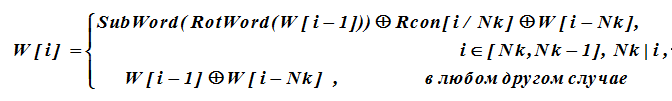 .
.
Para as palavras W [i] da chave, cujo índice é um múltiplo de Nk, os valores de W [i-1] estão sujeitos a uma transformação adicional antes de executar a operação XOR. Essa transformação é descrita da seguinte maneira.
A descrição da transformação contém funções:
RotWord () - deslocamento cíclico de bytes de uma palavra de 32 bits a (0) a (1) a (2) a (3) de acordo com a regra
{a (0) a (1) a (2) a (3)} → {a (3) a (0) a (1) a (2)};
SubWord () - substituição de bytes a (j) com elementos do bloco S da função SubBytes (), por exemplo, byte (af) é substituído por byte s (a, f) do bloco S; a ação é a mesma que ao processar uma mensagem,
Rcon [j] - o termo XOR é 2 j-1 .

Posições destacadas que são múltiplos de Nb, cujos valores são formados usando as funções SubWord (), RotWord (), Rcon (). As posições W [0] a W [3] são preenchidas de acordo com os dados iniciais fornecidos, todas as subseqüentes são calculadas de acordo com a razão para W [i].
Seleção de tecla redonda
Seleção de tecla redonda (RoundKeySelection). Para a rodada atual com o número r. A tecla redonda é escolhida como {W [Nb (r) -1], ..., W [Nb (r + 1) - 1]},
r = 1 (1) Nr.
Aqui, observamos que o algoritmo de criptografia geral fornece opções diferentes para conjuntos de variáveis Nb, Nk, Nr. Para uma implementação específica de uma versão fixa, ela pode ser significativamente simplificada. A tecla redonda pode ser computada em tempo real, o que não requer muita memória para armazenar toda a sequência W. Você pode limitar-se a um buffer de palavras Nk.
Exemplo 3 . Vamos explicar as proposições teóricas fornecidas com um exemplo numérico. Seja, como antes, Nb = Nk = 4, Nr = 10. A chave de cifra é dada como uma sequência hexadecimal K = 2b7e1516 282ed2a6 abf71588 09cf4f3c

A arquitetura “quadrada” e a computação orientada a bytes determinam a forma de sua apresentação na tabela a seguir.
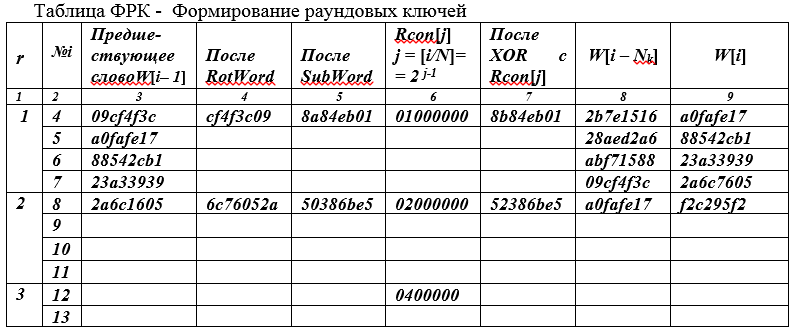
A coluna da esquerda é adicionada na tabela - número (r) da rodada.Na
primeira linha r = 1, i = 4, o byte anterior W [i-1] = W [3] é escrito na terceira coluna. o último byte da chave de cifra K. Como o índice i = 4 é um múltiplo de Nk = 4, na coluna 6 escrevemos (Rcon (J) = 01000000, j = [i / Nk] = 2 j-1 = 2 0 = 1) o valor 01 00 00 00 4- x palavra byte, cujo primeiro byte é 2 0 = 1, ou seja, 0000 0001, o restante dos bytes desta palavra de 32 bits é zero.
Na quarta coluna da tabela, insira os valores da coluna anterior, mas desloque ciclicamente 1 byte para a esquerda (rotação de palavras - RotWord). A quinta coluna contém o resultado da substituição de bytes dos valores da coluna anterior pelos valores de bytes do bloco S (função SubWord - substituir bytes). Depois disso, a adição de mod2 (XOR) é feita do conteúdo das colunas 5 e 6, 8a84eb01 + 0100 0000 = 8b84eb01, e o resultado da soma é inserido na coluna 7.
Na representação binária do byte 0000 0001 2 = 01 16, os bits menos significativos estão localizados à direita.
A coluna 8 contém o valor da palavra W [i-Nk] = W [0] (para a primeira linha, este é o valor da primeira palavra de 4 bytes (byte esquerdo) da chave de criptografia W [0]), que é adicionada pela operação XOR 8b 84 eb 01+ 2b 7e 15 16 = a0 fa fe 17 com conteúdo de 7 colunas. O resultado do somatório (coluna 9) é precisamente a primeira das quatro palavras de 4 bytes da tecla redonda da primeira rodada.
As outras três palavras da tecla redonda do primeiro turno são formadas sem o uso da função de deslocamento cíclico, substituição e Rcon [j], pois seus números não são múltiplos de Nk. O conteúdo da coluna 9 é transferido para a terceira coluna da próxima linha da tabela.
Definição de Rcon [j]. Este procedimento é realizado de acordo com um algoritmo especial, cujas ações ilustraremos com exemplos. O argumento j da função Rcon [j] é inteiro e é determinado pelo valor atual da variável i - o número da palavra-chave. Obviamente
j = 1, 2, 3, ... para i = Nk, 2Nk, 3Nk, ....
Como Nk em nosso exemplo é 4, temos valores inteiros de j para i = 4, 8, 12. Além disso, para cada número inteiro j, Rcon [j] = 2 j-1 = 1, 2, 4, 8, 16, ....
A duplicação de valores é permitida desde que Rcon [j] seja um elemento do campo GF (2 8 ).
Para i> 32, obtemos j> 8. Os valores fora do campo devem ser retornados ao campo. Isso é obtido reduzindo a representação polinomial dos elementos do campo Rcon [j] (modφ (x)).
Exemplo 4. Seja i = 32, 36, 40. Então j = 8, 9, 10. Esses valores estão fora do campo. Nós os devolvemos ao campo pelo módulo de redução φ (x) e calculamos os valores necessários.
Nós definimos os valores correspondentes de Rcon [j]. Os resultados do cálculo são resumidos em uma tabela.

Isso pode concluir a consideração das etapas para gerar chaves de criptografia AES redondas.