
Existem vários métodos para encontrar as raízes de uma equação polinomial de 4º grau.
No entanto, eles não são muito convenientes para resolver equações com coeficientes, que são expressões com parâmetros.
1. Fórmula para resolver uma equação de grau 4
Considere uma equação de 4º grau, cuja soma das raízes é igual a zero. Os coeficientes podem ser reais ou complexos.

O produto dos próximos dois quadrados é idêntico à equação considerada do 4º grau.
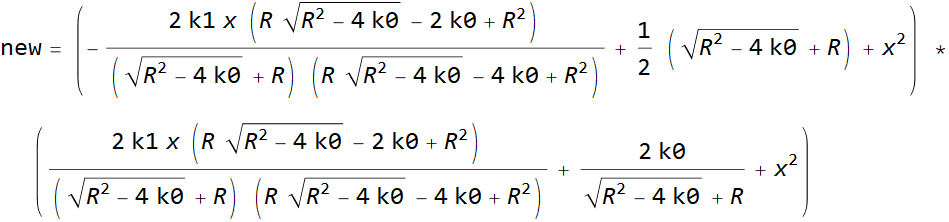
O valor R é a solução para a seguinte equação cúbica.
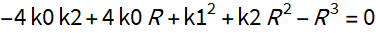
Quase a mesma equação aparece ao resolver uma equação de 4º grau por decomposição na diferença de quadrados perfeitos. Chamaremos essa equação cúbica de auxiliar.
Vamos calcular o produto de dois quadrados novos.
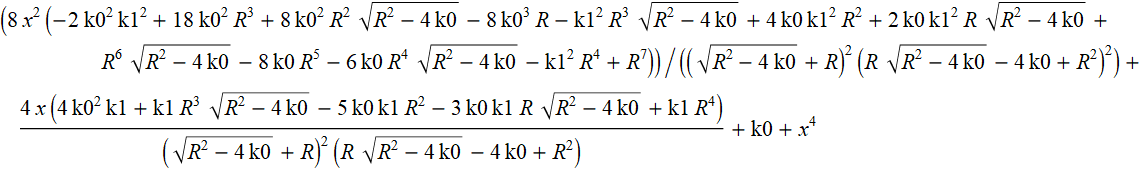
O mesmo, mas na forma de coeficientes em potências de x (em ordem decrescente de potências).
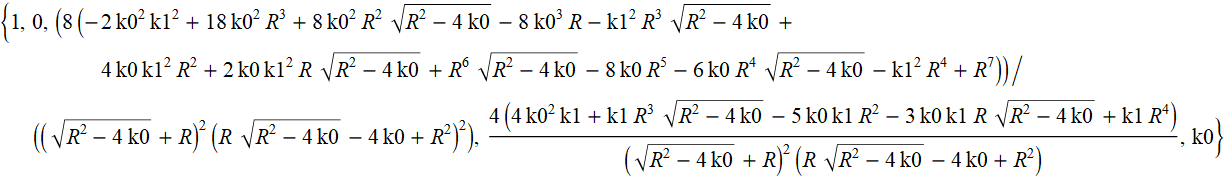
Vamos simplificar as expressões para os coeficientes na segunda e na primeira potências de x.
A expressão acima é para o primeiro grau de x.

Como resultado, obtemos k1.
A expressão acima é para a segunda potência de x.

Ou

Substituindo a expressão por R ^ 3, obtemos
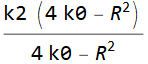
Or k2.
Portanto, new é idêntico à equação do 4º grau, cuja soma das raízes é igual a zero.
O problema com a equação cúbica auxiliar permanece.
Claro, métodos de solução tradicionais podem ser usados. Mas então será necessário transformar a equação para a forma canônica e considerar separadamente três soluções dependendo dos valores dos coeficientes. Isso nem sempre é conveniente para coeficientes que são expressões com parâmetros.
2. Solução da equação cúbica pelo método de transformação de Chirnhausen
Considere a solução da equação cúbica pelo método de transformação de Chirnhausen não muito difundido.
Então, resolvemos a equação original
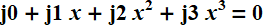
pelo método de Chirnhausen.
A essência do método consiste nas seguintes transformações.
1. A equação para y é introduzida
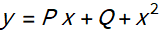
2. Ambos os lados da igualdade do item 1 são multiplicados por x

Em seguida, a expressão para x ^ 3 é substituída pela
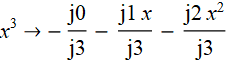
expressão

Em geral, as transformações descritas na Seção 2 não são idênticas. Mas se considerarmos apenas os valores de x, que são as raízes da equação original, interessantes, então essas transformações podem ser consideradas quase idênticas. E então y é representado por uma expressão correspondente às raízes da equação original.
3. Para uma equação cúbica, a operação no item 2 é realizada mais uma vez. Como resultado, um sistema de 3 equações em x é obtido, o qual possui três soluções diferentes de zero correspondentes às raízes da equação original. A partir dos coeficientes x, formamos a matriz
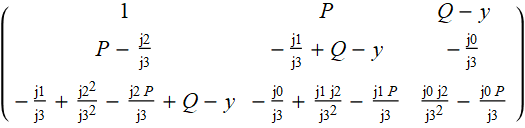
4. Encontre o determinante da matriz, que é representado por uma expressão cúbica em y.
Calculamos os valores que garantem a igualdade do determinante a zero.
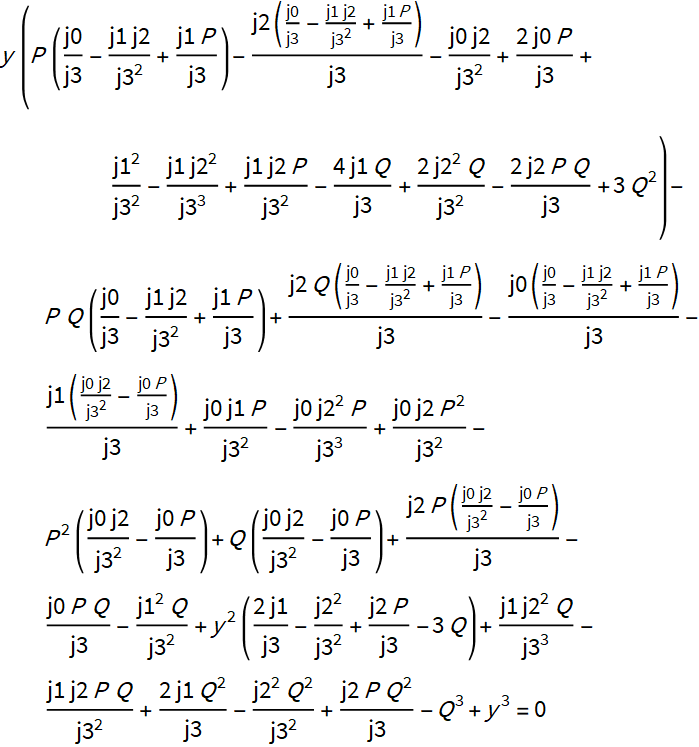
5. Na equação para y existem dois parâmetros P e Q. Vamos calculá-los de forma que os coeficientes no segundo e primeiro graus de y sejam iguais a zero.
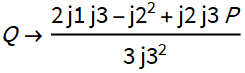
Qualquer P
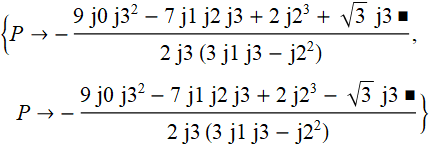
, onde

6. Como resultado, temos uma equação com três raízes múltiplas para y

7. Resta resolver uma equação quadrática com y, P, Q conhecido.
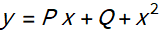
Uma das soluções será uma solução para a equação original.
3. Parâmetros para resolver a equação cúbica auxiliar
Para valores específicos dos coeficientes, nem tudo parece tão assustador.
Observe que apenas uma raiz R da equação cúbica auxiliar é necessária para a fórmula de resolução da equação de 4º grau.
Para coeficientes específicos da equação auxiliar, temos

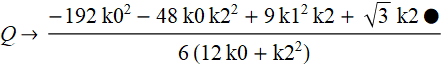
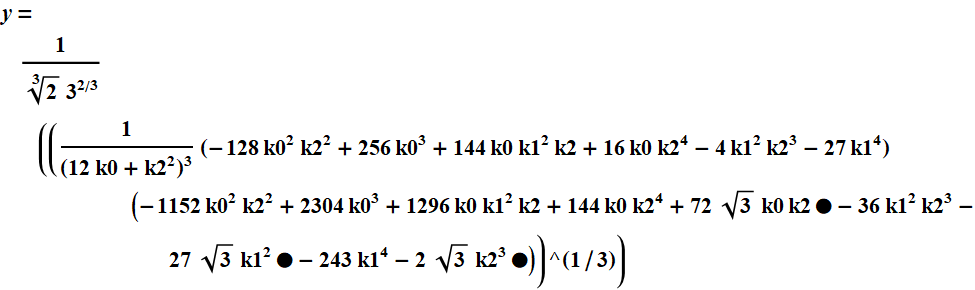

Ao usar a fórmula para resolver uma equação de 4º grau, é necessário consultar - "Método com métrica".
Envie tarefas interessantes para Direct Instagram .