“Recentemente, comecei a fazer experiências com o gnuplot e rapidamente fiz uma descoberta interessante. Plotei todos os primos abaixo de 1 milhão em coordenadas polares, então para cada primo p (r, θ) = (p, p). Não esperava nada de especial, apenas experimentei. Os resultados são impressionantes. "
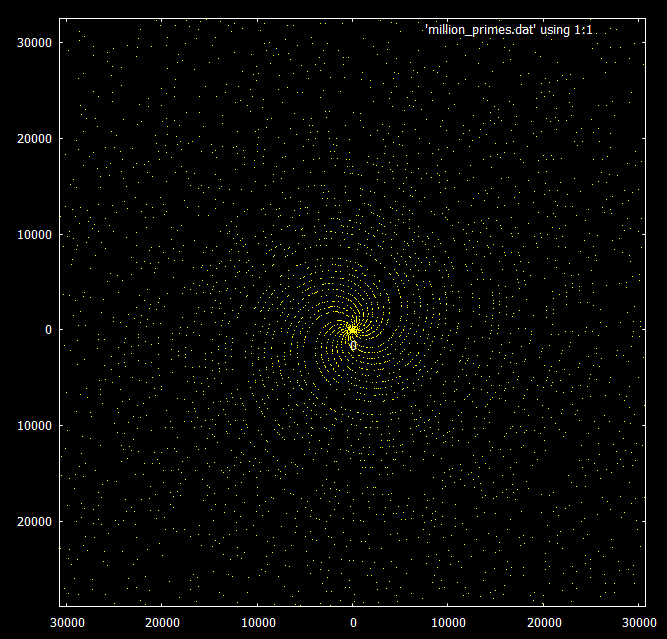
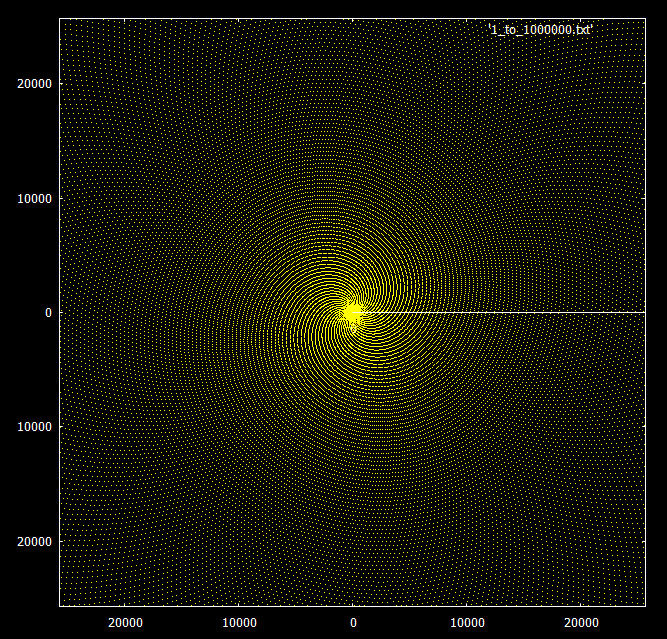
Se você olhar para os primos abaixo de 30.000, verá um padrão espiral.
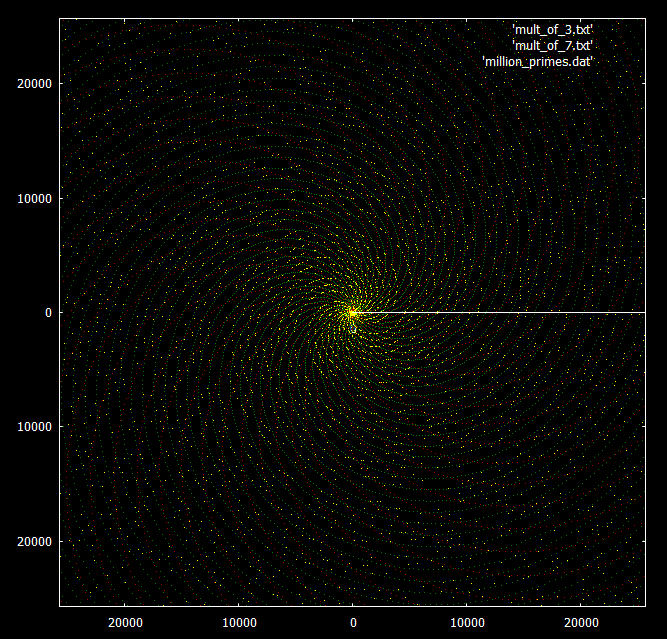
Para comparação - o mesmo gráfico com números sobrepostos, múltiplos de 3 e 7. Os números primos são destacados em amarelo, múltiplos de 3 e 7 - em verde e vermelho, respectivamente.

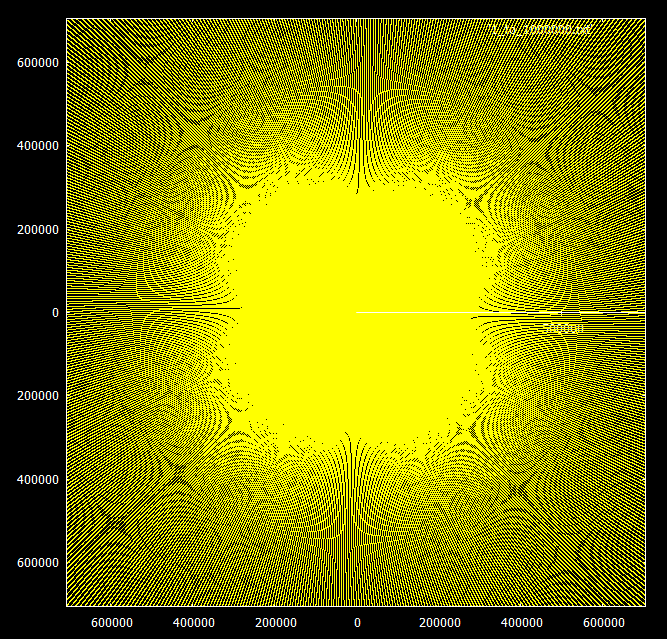
O que é realmente interessante é o comportamento ao aumentar o alcance. Os múltiplos desse número parecem espiralar no mesmo padrão até o infinito, mas os números primos começam a formar raios em grupos de 3 ou 4.
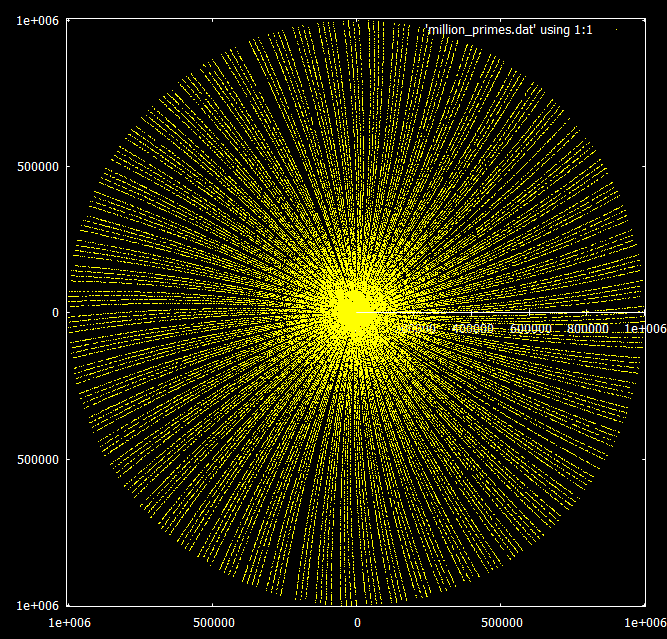
Comparados aos múltiplos de 3 e 7:
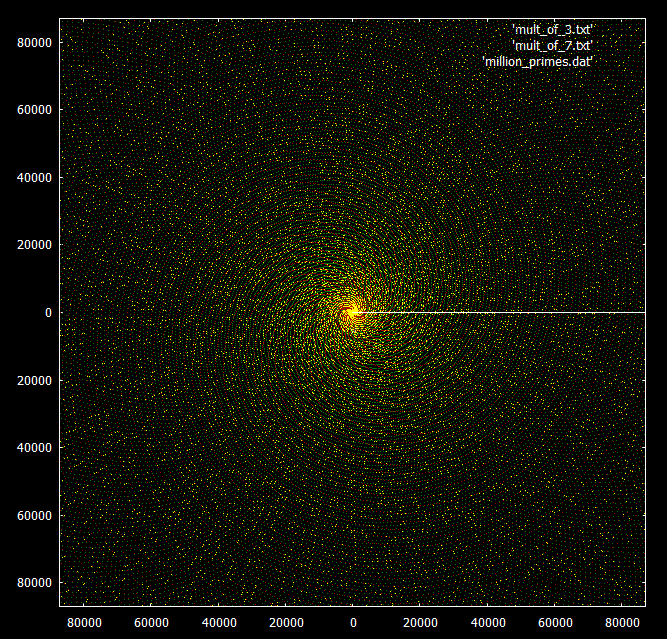
? , ?
. , , .
(, θ) = (n, n), n∈N
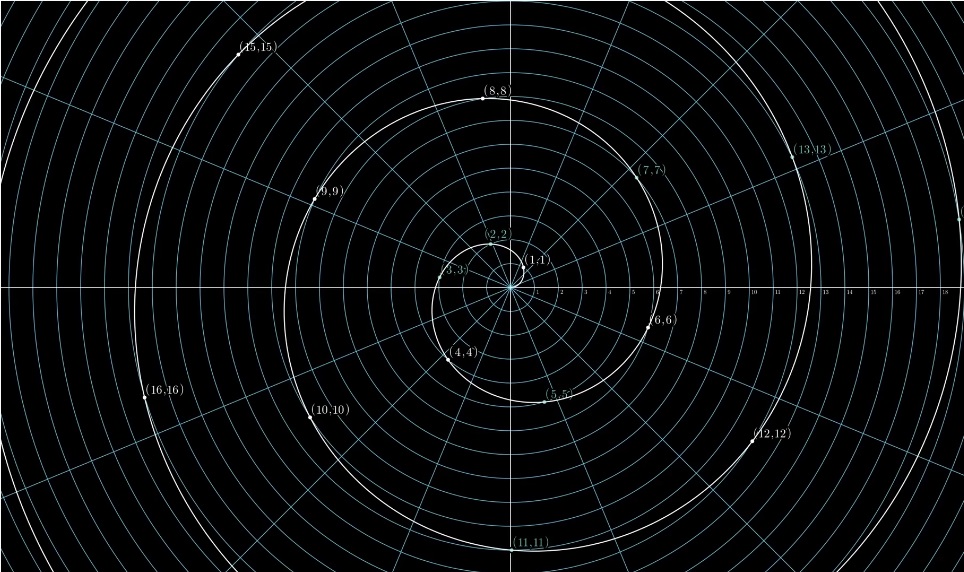
Para começar, você pode brincar com as coordenadas polares e considerar todos os pontos com coordenadas inteiras: (1,1) (2,2) ...
Obtemos a Espiral Arquimediana:
Se excluirmos todos os números, exceto os números primos, obteremos uma galáxia espiral com espaços:
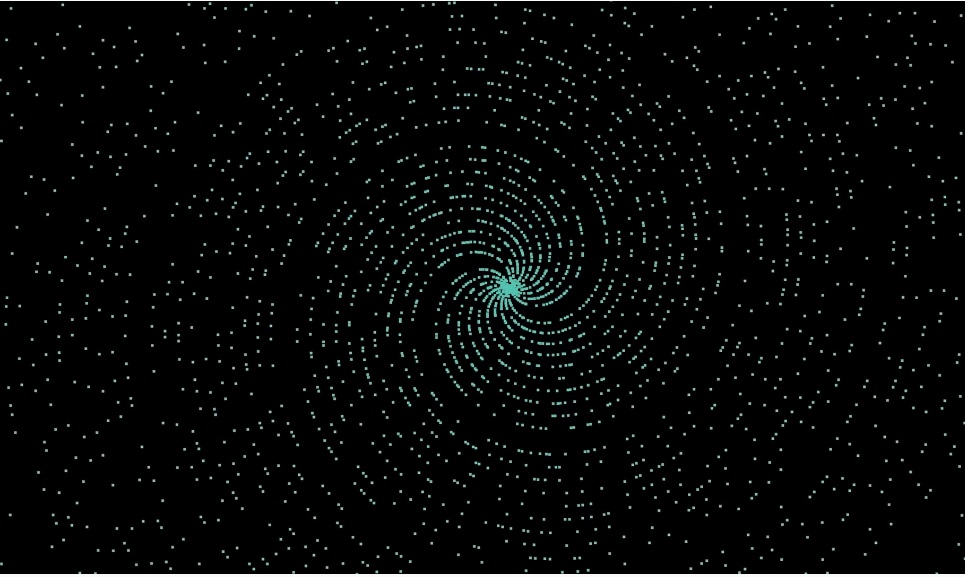
"Afastando-se", podemos para ver os raios dirigidos em todas as direções, principalmente em grupos de 4: As

espirais podem ser contadas, existem 20 deles:

E os raios 280:

Se tomarmos todos os números, não apenas os simples, então as espirais são ainda mais uniformes e existem 44:

Em um exame mais detalhado, temos 6 espirais:

Todos os números que são múltiplos de 6 formam um ramo:
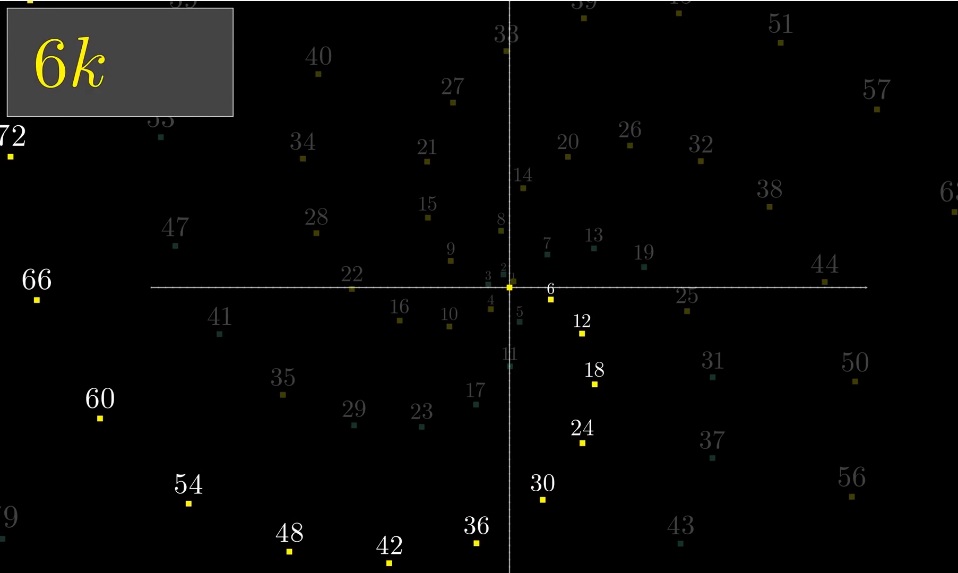
O resto dos braços espirais são 6k + 1, 6k + 2, etc. Por que é que? Porque 6 é aproximadamente igual a (revolução completa) 2ℼ (6,28318530718). Essa pequena diferença cria a ilusão de uma única curva.
Se você deixar apenas os primos, haverá apenas duas espirais (6k + 1 e 6k + 5):
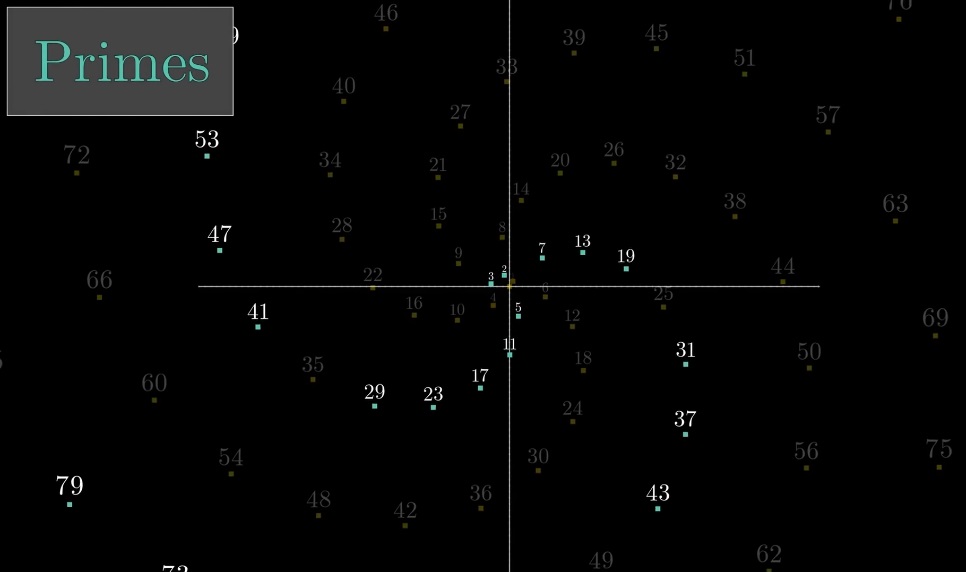
6 - quase um círculo completo, 44 - uma aproximação ainda mais precisa (44 / 2ℼ ≈ 7 círculos completos)
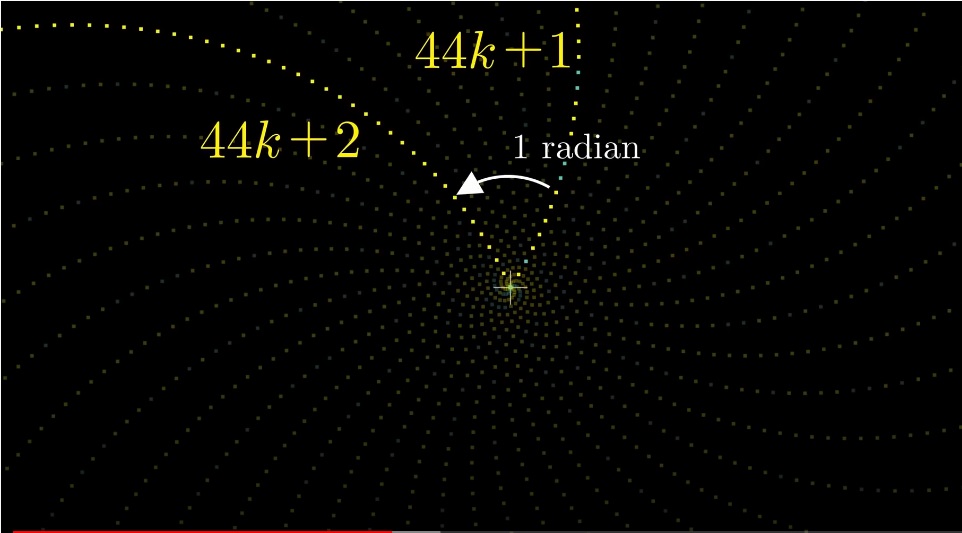
Apenas para os primos há 20 mangas (44k +1, 44k + 3, 44k + 5 ...). Função de Euler φ (44) =

20,710 / 2ℼ ≈ 113. (113,00000959)

Para os números primos, haverá lacunas:

quanto mais nos afastamos, mais claramente a curvatura de toda a estrutura se torna aparente.
710 = 71 * 5 * 2. Isso explica o agrupamento de 4 vigas (5) e os "dentes quebrados do pente" (71):

Função de Euler φ (710) = 280.
De acordo com o teorema de Dirichlet, os primos são uniformemente distribuídos nas mangas.
Conclusão
Brincando com a visualização, você pode tropeçar em a) Princípio de Dirichlet b) aproximar o número ℼ (e frações contínuas) c) alcançar a função de Euler.
A forma espiral é um artefato associado a um número par de radianos correspondentes.
Filme com dublagem em russo:
PS
Mais trabalho com números primos:
- Lacunas limitadas entre os primos . (Por Yitang Zhang, 2014)
- Primes em tuplas I (Por DANIEL A. GOLDSTON, JÁNOS PINTZ, e CEM Y. YILDIRIM, 2009)
Frações continuadas de Savvateev:
Alexey Savvateev "Tudo sobre como escrever números":