Controle de manipuladores multi-link de um complexo robótico usando uma rede neural

Introdução

Ao simular sistemas de controle de movimento para robôs, é necessário resolver os problemas de cinemática e dinâmica de seus atuadores. Existe um problema inverso e direto de cinemática. O problema direto da cinemática é determinar a posição espacial e a orientação do ponto característico, via de regra, da ferramenta de trabalho do robô manipulador pelos valores conhecidos das coordenadas generalizadas. O problema inverso da cinemática, como o problema direto, é um dos principais problemas da análise e síntese cinemática. Para controlar a posição dos elos e a orientação da ferramenta de trabalho do manipulador, torna-se necessário resolver o problema inverso da cinemática.

A maioria das abordagens analíticas para resolver o problema da cinemática inversa é bastante cara em termos de procedimentos computacionais. Uma das abordagens alternativas é o uso de redes neurais. Dados de entrada. Considere um manipulador de três elos com os parâmetros mostrados na Tabela 1.

Tabela 1 - Parâmetros DH para um manipulador de três links

No ambiente MatLab, usando o Robotics Toolbox distribuído gratuitamente, um modelo de computador de um manipulador de três links é construído. Abaixo está um fragmento do script MatLab no qual atribuímos ao array 'L' os valores dos parâmetros A, Alfa e D da Tabela 1. Para nosso modelo, esses são valores constantes e não mudam no processo de trabalho com o manipulador. Atribuímos o parâmetro Tetta à variável 'initialPose_left' - a posição inicial do nosso manipulador. 

function [L,initialPose_left,baseL] =model3z 
%   
initialPose_left = deg2rad([0 0 0]); 
L(1) = Revolute('d', 0.2, 'alpha', pi/2, 'qlim', initialPose_left(1)+deg2rad([-90 +90]) ); 
L(2) = Revolute('d', 0, 'alpha', 0, 'a', 0.4, 'qlim', initialPose_left(2)+deg2rad([-20 +90]));   
L(3) = Revolute('d', 0, 'alpha', 0, 'a', 0.4, 'qlim', initialPose_left(2)+deg2rad([-90 +90])); 
% -178 +178 
baseL = [1 0 0 0;  
        0 1 0 0;  
        0 0 1 0;  
        0 0 0 1]; 

1 (. 1) . 

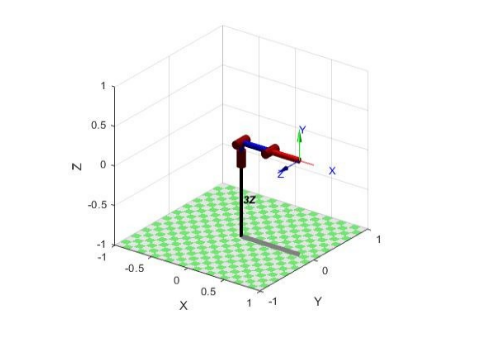
 Tetta, .  initialPose_left. 

. , . 

, .  

  . :

q – . 

%       
t1_min = L(1).qlim(1); t1_max = L(1).qlim(2);  
t2_min = L(2).qlim(1); t2_max = L(2).qlim(2); 
t3_min = L(3).qlim(1); t3_max = L(3).qlim(2); 
%     
t1 = t1_min + (t1_max-t1_min)*rand(N,1); 
t2 = t2_min + (t2_max-t2_min)*rand(N,1); 
t3 = t3_min + (t3_max-t3_min)*rand(N,1); 
Y = horzcat(t1, t2, t3);

, .  : 

:  x,y,z – . R – , . 

%    4x4 
T = zeros(4, 4, N); 
T(:, :, :) = leftArm.fkine(Y); %  ,       
%R = tr2rpy(T(1:3, 1:3, :), 'arm'); %      
R = tr2eul(T(1:3, 1:3, :)); %      
Tx = reshape(T(1, 4, :), [N 1]); %  - 
Ty = reshape(T(2, 4, :), [N 1]); 
Tz = reshape(T(3, 4, :), [N 1]); 
% scatter3(Tx,Ty,Tz,'.','r'); 
X = horzcat(Tx, Ty, Tz, R); %   

. 3.2.1  , 3000 . 

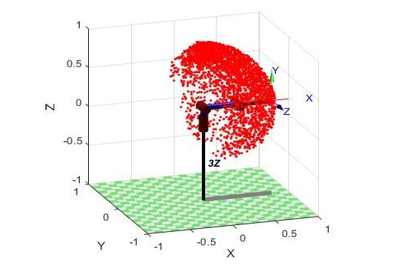
, 3000 . , X Y. 

, .

Keras Python. .

X_train, X_test, y_train, y_test = train_test_split(data_x, data_y, test_size=0.2,
random_state=42) 

« » . .

def base_model():
 model = Sequential()
 model.add(Dense(32,input_dim=6,activation='relu'))
 model.add(Dense(64,activation='relu'))
 model.add(Dense(128,activation='relu'))
 model.add(Dense(32,activation='relu'))
 model.add(Dense(3, init='normal'))
 model.compile(loss='mean_absolute_error', optimizer = 'adam', metrics=['accuracy'])
 model.summary()
 return model

, . . , , . , , .       KerasRegressor,  Keras.

clf = KerasRegressor(build_fn=base_model, epochs=500, batch_size=20,verbose=2)
clf.fit(X_train,y_train) 

.

res = clf.predict(X_test) 

99% , . 

3 , , , . . , . . - . , , , , .

%%    ,    
M=[-178:10:178]; %      -178   +178    10 
M_size=length(M); 
first_q=zeros(M_size, 3); 
T33 = zeros(4, 4, M_size); 
T34 = zeros(4, 4, M_size); 
first_q(:,1)=[deg2rad(M)]; %  q 
T33(:, :, :) = leftArm.fkine(first_q);%      ,   
R = tr2rpy(T33(1:3, 1:3, :), 'arm'); %      
Tx = reshape(T33(1, 4, :), [M_size 1]); %  - 
Ty = reshape(T33(2, 4, :), [M_size 1]); 
Tz = reshape(T33(3, 4, :), [M_size 1]); 
plot3(Tx,Ty,Tz) 
axis([-1 1 -1 1 -1 1]);hold on;grid on; 

XX = horzcat(Tx, Ty, Tz, R); %        
T34(:, :, :) = leftArm.fkine(q_new); %     ,   
Tx2 = reshape(T34(1, 4, :), [M_size 1]); %  - 
Ty2 = reshape(T34(2, 4, :), [M_size 1]); 
Tz2 = reshape(T34(3, 4, :), [M_size 1]); 
plot3(Tx2,Ty2,Tz2,'.') 
axis([-1 1 -1 1 -1 1])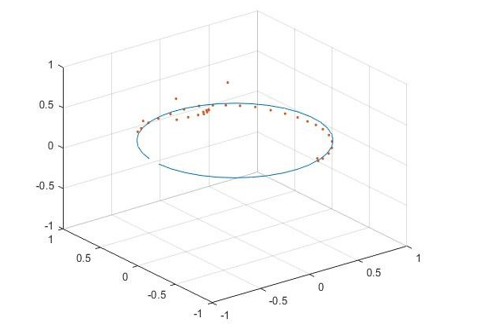 

. . , - . , . . «Programming by demonstration», . Matlab , – .