Como sabemos se o algoritmo funciona?
Antes de desenvolver um algoritmo, você precisa pensar em como avaliaremos seu desempenho. Digamos que escrevemos um algoritmo e ele diz que "esta imagem tem as seguintes cores" - a decisão dele será correta? E o que isso significa - "correto"?
Para resolver este problema, escolhemos duas dimensões importantes - a marcação correta da cor primária e o número correto de cores. Definimos isso como a distância CIEDE 2000 ( fórmula de diferença de cor ) entre a cor de primeiro plano prevista por nosso algoritmo e nossa cor de primeiro plano real, e também calculamos o erro absoluto médio no número de cores. Fizemos essa escolha pelos seguintes motivos:
- Esses parâmetros são fáceis de calcular.
- Conforme o número de métricas aumentasse, seria mais difícil escolher o “melhor” algoritmo.
- Ao reduzir o número de métricas, podemos estar perdendo uma diferença importante entre os dois algoritmos.
- Em qualquer caso, a maioria das roupas tem uma ou duas cores primárias e muitos de nossos processos dependem de uma cor primária. Portanto, calcular a cor de base corretamente é muito mais importante do que calcular a segunda ou terceira cor corretamente.
E os dados "reais"? Nossa equipe de comerciantes nos forneceu rótulos, mas nossas ferramentas permitem que eles escolham apenas as cores mais comuns, como "cinza" ou "azul" - elas não podem ser chamadas de um valor exato. Essas definições gerais incluem alguns tons diferentes, portanto, não podem ser usadas como cores reais. Teremos que construir nosso próprio conjunto de dados.
Alguns de vocês já devem estar pensando em serviços como o Mechanical Turk. Mas não precisamos marcar muitas imagens, portanto, descrever esta tarefa pode ser ainda mais difícil do que apenas concluí-la. Além disso, criar um conjunto de dados ajuda a entendê-lo melhor. Nós rapidamente confundimos um aplicativo HTML / Javascript e selecionamos aleatoriamente 1000 imagens, selecionadas para cada pixel que representa sua cor primária, e marcamos o número de cores que vimos na imagem. Depois disso, ficou fácil obter dois números avaliando a qualidade do nosso algoritmo (distância até a cor principal CIEDE e o número de cores MAE).
Às vezes, verificamos os programas manualmente, executando os dois algoritmos em uma imagem e exibindo duas listas de cores. Em seguida, classificamos manualmente 200 imagens, escolhendo quais cores foram reconhecidas como “melhores”. É muito importante trabalhar em estreita colaboração com os dados desta forma - não apenas para obter o resultado ("Algoritmo B funcionou melhor do que o Algoritmo A em 70% dos casos"), mas também para compreender o que acontece em cada um dos casos ("O Algoritmo B normalmente escolhe muitos grupos, mas Algoritmo A perde cores claras ”).

Suéter e cores selecionadas por dois algoritmos diferentes
Nosso algoritmo de extração de cores
Antes de processar as imagens, nós as convertemos para o espaço de cores CIELAB (ou apenas LAB) em vez do RGB mais comum. Como resultado, nossos três números não representarão a quantidade de vermelho, verde e azul. Os pontos do espaço LAB (L * a * b * seria mais correto, mas escreveremos LAB para simplificar) designam três eixos diferentes. L denota brilho de preto 0 a branco 100. A e B denotam cor: A denota uma localização na faixa de -128 verde a 127 vermelho, e B de -128 azul a 127 amarelo.A principal vantagem deste espaço é a uniformidade percebida. A distância ou diferença entre dois pontos no espaço LAB será percebida da mesma, independente de sua localização, se a distância euclidiana entre eles no espaço também for a mesma.
Naturalmente, o LAB tem outros problemas: por exemplo, consideramos imagens em telas de computador que usam espaço RGB específico de dispositivo. Além disso, a gama LAB é mais ampla do que RGB, ou seja, em LAB você pode expressar cores que não podem ser expressas por RGB. Portanto, a conversão de LAB em RGB não pode ser bilateral - ao converter um ponto em uma direção e depois na direção oposta, você pode obter um valor diferente. Teoricamente, essas deficiências estão presentes, mas na prática o método ainda funciona.
Ao converter a imagem para LAB, obteremos um conjunto de pixels que podem ser vistos como pontos (L, A, B, X, Y). O resto do algoritmo se preocupa com o agrupamento desses pontos, nos quais os grupos do primeiro estágio usam todas as cinco medidas e o segundo estágio omite as medidas X e Y.
Agrupamento no espaço
Começamos com uma imagem sem agrupamento de pixels, com correção de cor conforme descrito no artigo anterior , compactada para 320x200 e convertida para LAB.

Primeiro, vamos aplicar o algoritmo Quickshift, que agrupa os pixels próximos em "superpixels".

Isso já reduz nossa imagem de 60.000 pixels a algumas centenas de superpixels, removendo a complexidade desnecessária. Você pode simplificar a situação ainda mais mesclando superpixels próximos com uma pequena distância de cor entre eles. Para fazer isso, desenhamos seu gráfico de proximidade regional - um gráfico no qual os nós que denotam dois superpixels diferentes são conectados por uma aresta se seus pixels se tocam.

– (Regional Adjacency Graph, RAG) . , , , , . , , , , . – , .
Os nós do gráfico são os superpixels que calculamos e as bordas são a distância entre eles no espaço de cores. Uma borda conectando dois superpixels próximos com cores semelhantes terá um peso baixo (linhas escuras), e uma borda entre superpixels com cores muito diferentes terá um peso alto (linhas brilhantes, bem como a ausência de linhas - elas não foram desenhadas se seu peso fosse superior a 20). Há muitas maneiras de combinar superpixels próximos, mas um limite simples de 10 foi o suficiente para nós.
Em nosso caso, conseguimos reduzir 60.000 pixels para 100 áreas, cada uma das quais contendo pixels da mesma cor. Isso oferece vantagens computacionais: primeiro, sabemos que um grande superpixel de cor quase branca é o fundo e pode ser removido. Removemos todos os superpixels com L> 99 e A e B no intervalo de -0,5 a 0,5. Em segundo lugar, podemos reduzir bastante a contagem de pixels na próxima etapa. Não seremos capazes de reduzir seu número para 100, pois precisamos pesar as áreas com base no número de pixels que contêm. Mas podemos remover facilmente 90% dos pixels de cada grupo sem perder muitos detalhes e quase nenhuma distorção do próximo agrupamento.
Agrupando sem usar espaço
Nesta etapa, temos vários milhares de pixels com coordenadas (L, A, B). Existem muitas técnicas que podem agrupar esses pixels de maneira adequada. Escolhemos o método k-means porque é rápido, fácil de entender, nossos dados têm apenas 3 dimensões e a distância euclidiana no espaço LAB faz sentido.
Não éramos muito espertos e tínhamos um agrupamento com K = 8. Se algum grupo contiver menos de 3% dos pontos, tentamos novamente, desta vez com K = 7, depois 6 e assim por diante. Como resultado, temos uma lista de 1 a 8 centros de agrupamento e uma fração do número de pontos pertencentes a cada um dos centros. Eles são nomeados pelo algoritmo colornamer descrito no artigo anterior.
Resultados e problemas restantes
Atingimos uma distância média de 5,86 na escala CIEDE 2000 entre a cor prevista e a “real”. É bastante difícil interpretar corretamente este indicador. Na métrica de distância CIE76 simples , nossa distância média é 7,82. Nesta métrica, um valor de 2,3 representa uma diferença sutil. Portanto, podemos dizer que nossos resultados, ligeiramente acima de 3, indicam uma diferença sutil.
Além disso, nosso MAE foi de 2,28 cores. Mas, novamente, esta é uma métrica secundária. Muitos algoritmos descritos abaixo reduzem esse erro, mas à custa de aumentar a distância da cor. É muito mais fácil ignorar as cores falsas do 5º ou 6º lugar do que ignorar a primeira cor errada.

Mesmo coisas que são claramente da mesma cor, como esses shorts, contêm áreas que parecem muito mais escuras devido
às sombras. O problema das sombras permanece. O tecido não pode ser colocado perfeitamente uniformemente, portanto, parte da imagem sempre permanecerá na sombra e parecerá enganosamente de uma cor diferente. As abordagens mais simples, como encontrar cores duplicadas da mesma tonalidade e brilho diferente, não funcionam, uma vez que a transição de “pixel sem sombra” para “pixel na sombra” nem sempre funciona da mesma maneira. No futuro, esperamos usar técnicas mais sofisticadas como DeshadowNet ou reconhecimento automático de sombras .

Nos concentramos apenas na cor das roupas. Joias e sapatos têm seus próprios problemas: nossas fotos de joias são muito pequenas e as fotos de sapatos geralmente mostram o interior deles. No exemplo acima, indicaríamos a presença de bordô e ocre na foto, embora apenas o primeiro deles seja importante.
O que mais nós tentamos
Este último algoritmo parece muito simples, mas não foi fácil de criar! Nesta seção, descreverei as opções que tentamos e com as quais aprendemos.
Remoção de fundo
Tentamos algoritmos de remoção de fundo - por exemplo, o algoritmo de Lyst . A avaliação informal mostrou que eles não funcionaram com tanta precisão quanto simplesmente remover o fundo branco. No entanto, planejamos estudá-lo mais profundamente à medida que processamos imagens nas quais nosso estúdio fotográfico não trabalhou.
Hashing pixels
Algumas bibliotecas de extração de cores escolheram uma solução simples para este problema: agrupar pixels fazendo o hash deles em vários recipientes suficientemente largos e, em seguida, retornar os valores médios dos recipientes LAB com mais pixels. Experimentamos a biblioteca Colorgram.py; apesar de sua simplicidade, funciona surpreendentemente bem. Além disso, ele funciona rapidamente - não mais do que um segundo por imagem, enquanto nosso algoritmo gasta dezenas de segundos por imagem. No entanto, Colorgram.py tinha uma distância média maior para a cor base do que nosso algoritmo - principalmente porque seu resultado é obtido a partir das distâncias médias para grandes contêineres. No entanto, às vezes o usamos para casos em que a velocidade é mais importante do que a precisão.
Outro algoritmo de divisão de superpixel
Usamos o algoritmo Quickshift para segmentar a imagem em superpixels, mas existem vários algoritmos possíveis - por exemplo, SLIC, Watershed e Felzenszwalb. Na prática, Quickshift tem mostrado os melhores resultados graças ao seu trabalho com peças pequenas. Por exemplo, o SLIC tem um problema com coisas como listras que ocupam muito espaço na imagem. Aqui estão os resultados indicativos do algoritmo SLIC com diferentes configurações: Compacidade da

imagem original

=

compactação 1 = compactação 10

= 100
Para trabalhar com nossos dados, Quickshift tem uma vantagem teórica: não requer comunicação contínua de superpixel. Os pesquisadores notaram que isso pode causar problemas para os algoritmos, mas, em nosso caso, é uma vantagem - muitas vezes nos deparamos com pequenas áreas com pequenos detalhes que queremos trazer para um grupo.

Camisa

quadriculada Seu agrupamento de superpixel da Quickshift
Enquanto o agrupamento de superpixel da Quickshift parece caótico, na verdade ele agrupa todas as listras vermelhas com outras vermelhas, azuis com azuis, etc.
Diferentes métodos de contagem do número de grupos
Ao usar o método k-means, surge a pergunta mais comum: como fazer "k"? Ou seja, se precisarmos agrupar pontos em um certo número de grupos, quantos devemos fazer? Várias abordagens foram desenvolvidas para responder à pergunta. O mais simples é o “método do cotovelo”, mas requer processamento manual do gráfico e precisamos de uma solução automática. O Gap Statistic formaliza este método, e com ele obtivemos os melhores resultados na métrica "número de cores", mas às custas da precisão da cor base. Como a cor principal é a mais importante, não a usamos no programa de trabalho, mas planejamos estudar esse assunto mais a fundo.
Finalmente, o método da silhueta é outro método popular de seleção k. Ele fornece resultados um pouco piores do que nosso algoritmo e tem uma séria desvantagem: precisa de pelo menos 2 grupos. Mas muitas peças de roupa têm apenas uma cor.
DBSCAN
Uma solução potencial para a questão de escolher k é usar um algoritmo que não exija que você escolha esse parâmetro. Um exemplo popular é o DBSCAN, que procura grupos de densidade aproximadamente igual nos dados.

Blusa multicolorida
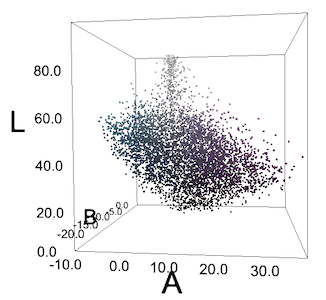
Todos os pixels da imagem dela estão no espaço LAB. Os pixels não formam grupos ciano e violeta claros.
Freqüentemente, não recebemos esses grupos ou vemos algo como grupos apenas por causa das peculiaridades da percepção humana. Para nós, os "pepinos" azul-esverdeados na blusa se destacam contra o fundo roxo, mas se plotarmos todos os pixels em coordenadas RGB ou LAB, eles não formarão grupos. Mas tentamos DBSCAN de qualquer maneira com diferentes valores de epsilon - e obtivemos resultados previsivelmente ruins.
Solução da Algolia
Um dos bons princípios dos pesquisadores é ver se alguém já resolveu o seu problema. Leo Ercolanelli, do site Algolia , publicou uma descrição detalhada da solução para esse problema há mais de três anos. Graças à sua generosidade na distribuição de fontes, pudemos experimentar a solução por conta própria. No entanto, os resultados foram um pouco piores do que os nossos, então deixamos nosso algoritmo. Eles não resolvem o mesmo problema que nós: eles tinham imagens de produtos em modelos e contra um fundo diferente do branco, então faz sentido que seus resultados sejam diferentes dos nossos.
Coordenação de cores
Este algoritmo completa o processo descrito em nosso artigo anterior. Depois de extrair os centros de grupo, usamos Colornamer para nomeá-los e, em seguida, importar essas cores para nossas ferramentas internas. Isso nos ajuda a visualizar facilmente nossos produtos por cor; esperamos incorporar esses dados aos algoritmos de recomendação de compra. Esse processo não é perfeito; ele nos ajuda a obter dados melhores sobre nossos milhares de produtos, o que, por sua vez, contribui para nosso objetivo principal de ajudar as pessoas a encontrar os estilos que amam.
Entrevista sobre a tradução da primeira parte