🔳 🙏 😶 Representação geométrica da curvatura do espaço na métrica de Schwarzschild 🛶 ☔️ ↔️

... ou dois mais dois é igual a quatro.

Para entender o artigo, basta um curso escolar de matemática.

A forma multiplicadora na métrica Schwarzschild há muito me assombra com sua duplicidade primorosa, e decidi dedicar algum tempo para encontrar maneiras de transformá-la. A própria métrica de Schwarzschild é obtida como resultado da resolução da relatividade geral para o caso do vácuo (o tensor de energia-momento é zero):

d s^{2} = - (1 - 2 \frac{G M}{c^{2} r}) c^{2} d t^{2} + {(1 - 2 \frac{G M}{c^{2} r})}^{- 1} d r^{2} + r^{2} \cdot d θ^{2} + r^{2} \cdot \sin^{2} θ \cdot d ϕ^{2}

Ele descreve o contínuo espaço-tempo na vizinhança de um objeto massivo compacto arbitrário. Compacto, o que significa que os desvios da forma são insignificantes em relação à massa. Simplificando, redondo e apertado. Normalmente, um buraco negro é usado aqui como exemplo. Por alguma razão, ninguém dá exemplos de objetos não compactos. Uma vara de espuma hermética em um espaço aberto a uma distância infinita de objetos enormes, como um objeto não compacto. O cavalo cubo à distância, de onde você também pode ver a tristeza em seus olhos.

Através do volume da 3-esfera

Faremos uma substituição:

M = \frac{E}{c^{2}}

Então, a métrica ficará assim:

d s^{2} = - (1 - 2 \frac{G E}{c^{4} r}) c^{2} d t^{2} + {(1 - 2 \frac{G E}{c^{4} r})}^{- 1} d r^{2} + r^{2} \cdot d θ^{2} + r^{2} \cdot \sin^{2} θ \cdot d ϕ^{2}

A substituição foi necessária apenas para chamar a atenção para o quarto grau da velocidade da luz, porque todos os números nas fórmulas importam. Isso é evidenciado por toda a história da física - qualquer fórmula obtida empiricamente ao longo do tempo recebe uma base teórica que explica os significados de todas as formas matemáticas nela contidas.

Normalmente, na representação dessa métrica, a parte associada às constantes físicas e à massa do corpo que cria o campo é expressa em termos do raio de Schwarzschild:

r_{s} = 2 \cdot \frac{G E}{c^{4}}

porque a métrica tem uma singularidade neste ponto. Aqui, o tempo pára literalmente.

É assim que toda a métrica se parece:

d s^{2} = - (1 - \frac{r_{s}}{r}) c^{2} d t^{2} + {(1 - \frac{r_{s}}{r})}^{- 1} d r^{2} + r^{2} \cdot d θ^{2} + r^{2} \cdot \sin^{2} θ \cdot d ϕ^{2}

Mas na continuação do raciocínio sobre a essência física dos fenômenos, estes dois:

r_{s} = 2 \cdot \frac{G E}{c^{4}}

também deve ser compreendido. Portanto, nós o representamos assim:

u = \frac{G E}{c^{4}}

É apenas metade do raio gravitacional

r_{s}

, e sua dimensão é a mesma. Nós temos:

1 - 2 \frac{G E}{c^{4} r} = 1 - 2 \frac{u}{r}

Ele se sugere:

= (1 - 2 \frac{u}{r} + \frac{u^{2}}{r^{2}}) - \frac{u^{2}}{r^{2}} = {(1 - \frac{u}{r})}^{2} - \frac{u^{2}}{r^{2}} = {(\frac{r - u}{r})}^{2} - \frac{u^{2}}{r^{2}} =

= \frac{(r - u)^{2} - u^{2}}{r^{2}} (1)

Já não está mal. Vamos desenhar. Imagine

r = O B

segmento final,

u = O A

- parte dele, conforme mostrado na figura abaixo. É obvio que

(r - u) = A B

...

É curioso, aliás, qual dos

r_{s} = 2 u

segue-se que o ponto

A

está localizado atrás (abaixo) do horizonte de eventos do objeto de energia

E

... É tão fácil encontrar, mas não podemos.

Agora vamos mostrar que uma relação da forma

(1)

será executado para todos os pontos tendo um lugar geométrico na perpendicular a

O B

no ponto

A

\frac{(r - u)^{2} - u^{2}}{r^{2}} = \frac{((r - u)^{2} + a^{2}) - (u^{2} + a^{2})}{r^{2}} = \frac{b^{2} - d^{2}}{r^{2}} (2)

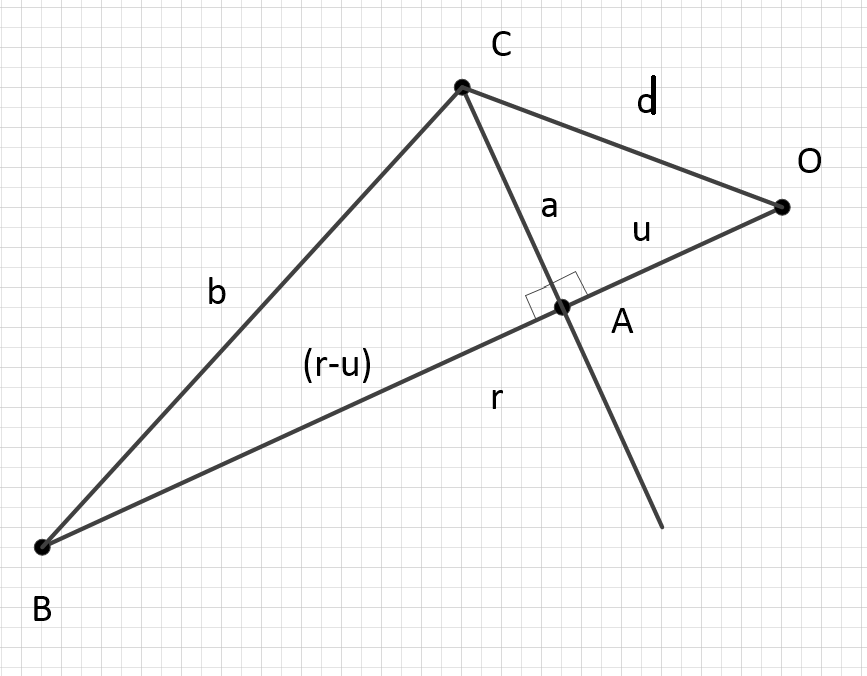
para qualquer

b = C B

d = O C

...

Simplificando, a diferença de quadrados

(r - u)^{2} - u^{2}

é equivalente à diferença de quaisquer quantidades cujas projeções sobre

O B

estamos

A B

O A

respectivamente, desde que o ponto

C

eles têm em comum.

Além disso, suponha que

u = u (E)

(r - u)

inversamente, projeções

r = O B

em alguns eixos, isto é, a soma pitagórica de duas grandezas, em sua forma original, perpendiculares entre si. Traduzir isso em um requisito, considere o caso

∠ O C B = π / 2

para o qual é verdade:

b^{2} = r^{2} - d^{2} \to (2) \to \frac{b^{2} - d^{2}}{r^{2}} = 1 - 2 \frac{d^{2}}{r^{2}} (3)

Vamos finalizar

(3)

semelhante à iteração inicial:

1 - 2 \frac{d^{2}}{r^{2}} = (1 - 2 \frac{d^{2}}{r^{2}} + \frac{d^{4}}{r^{4}}) - \frac{d^{4}}{r^{4}} = \frac{(r^{2} - d^{2})^{2} - d^{4}}{r^{4}} =

= \frac{b^{4} - d^{4}}{{\sqrt{b^{2} + d^{2}}}^{4}} = \frac{b^{4} - d^{4}}{r^{4}} (4)

Aqui está o quarto grau. Fórmula para o volume de uma esfera 3:

V = \frac{π^{2} \cdot R^{4}}{2}

Quero dizer que se você multiplicar e dividir

(4)

π^{2} / 2

\frac{b^{4} - d^{4}}{r^{4}} = \frac{π^{2}}{2} \cdot \frac{2}{π^{2}} \cdot \frac{b^{4} - d^{4}}{r^{4}} = \frac{V_{b} - V_{d}}{V_{r}} (5)

então, o fator na métrica de Schwarzschild se transforma na diferença entre os volumes de duas esferas 3 construídas em torno de duas projeções radiais de um ponto em relação ao centro do campo, correlacionado ao volume de uma esfera 3 formada pela distância total entre o ponto e o centro do campo.

Tendo em conta que o raio total é dado por projecções, toda esta construção é definida de forma muito sucinta por dois parâmetros, um dos quais relacionado com a energia e o segundo não. Existem exatamente duas coordenadas.

conclusões

As consequências notáveis de tal representação são:

1. Da forma do multiplicador, vê-se que o comportamento do fóton limita a zona visível do espaço-tempo pentadimensional. Fora dele, você pode esconder algo gravitando, mas invisível.

2. A presença da segunda coordenada oculta elimina o paradoxo do tempo zero.

3. Uma vez que a curvatura do espaço em torno de um corpo maciço pode sempre ser decomposta em dois componentes, um dos quais está associado à energia do corpo e o segundo exclusivamente ao espaço, então a próxima etapa é resolver as equações da relatividade geral para o caso do vácuo do espaço-tempo pentadimensional. Mais sobre isso no próximo artigo.

Bônus. Do outro lado da esquina

Obviamente, é possível expressar o significado do campo em um ponto por meio de um ângulo plano, que expressa o desvio da trajetória do movimento do espaço plano (na ausência de campos gravitacionais).

Vamos expressar as quantidades

b

d

do outro lado da esquina

α = ∠ O B C

b = r \cdot \cos α; d = r \cdot \sin α

... Vamos chamá-lo de ângulo de curvatura da trajetória. Então, o fator pode ser expresso de maneiras muito diferentes:

1 - 2 \frac{G E}{c^{4} r} = \cos^{2} α - \sin^{2} α = \cos^{4} α - \sin^{4} α = 1 - 2 \sin^{2} α =

= \frac{1 - \tan^{2} α}{1 + \tan^{2} α} = \cos 2 α (6)

Gosto especialmente da versão tangente.

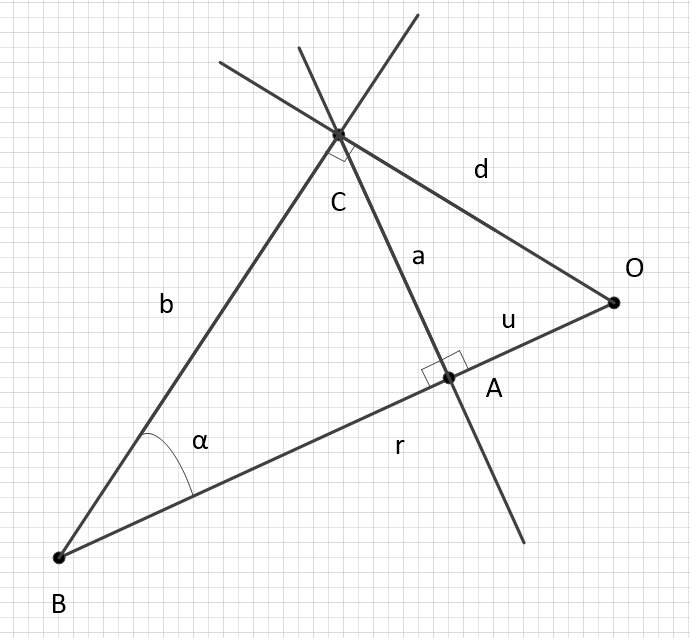
imagem

Substitua no intervalo original:

d s^{2} = - \cos 2 α \cdot c^{2} d t^{2} + \cos^{- 1} 2 α \cdot d r^{2} + r^{2} \cdot d θ^{2} + r^{2} \cdot \sin^{2} θ \cdot d ϕ^{2}

Tudo, como deveria, se transforma em uma métrica Minkowski plana para

α = 0

...

Definitivamente deveria haver um quinto ...

Continua.

Representação geométrica da curvatura do espaço na métrica de Schwarzschild

Através do volume da 3-esfera

conclusões

Bônus. Do outro lado da esquina

More articles: