HDTree: uma árvore de decisão personalizada em Python

Apresentando uma estrutura de árvore de decisão interativa e personalizável escrita em Python. Essa implementação é adequada para extrair conhecimento dos dados, testar a intuição, melhorar sua compreensão do funcionamento interno das árvores de decisão e explorar relações alternativas de causa e efeito para seu problema de aprendizagem. Ele pode ser usado como parte de algoritmos, visualizações e relatórios mais complexos, para qualquer propósito de pesquisa e como uma plataforma acessível para testar facilmente suas idéias de algoritmos de árvore de decisão.



TL; DR

• Repositório HDTree
• Bloco de notas complementar no interior examples. O diretório do repositório está aqui (todas as ilustrações que você vê aqui serão geradas no bloco de notas). Você mesmo pode criar ilustrações.

Sobre o que é a postagem?

Outra implementação de árvores de decisão que escrevi como parte de minha tese. O trabalho está dividido em três partes da seguinte forma: 

• Tentarei explicar por que decidi levar meu tempo para criar minha própria implementação de árvores de decisão. Vou listar alguns de seus recursos , mas também as desvantagens da implementação atual.
• Vou mostrar o uso básico do HDTree com alguns trechos de código e alguns detalhes explicados ao longo do caminho.
• Dicas sobre como personalizar e estender o HDTree com suas ideias.

Motivação e histórico

Para minha dissertação, comecei a trabalhar com árvores de decisão. Meu objetivo agora é implementar um modelo de ML centrado no ser humano em que HDTree (Human Decision Tree, nesse caso) é um ingrediente adicional que é aplicado como parte da IU real para esse modelo. Embora esta história seja exclusivamente sobre HDTree, eu poderia escrever uma sequência detalhando os outros componentes.

Recursos HDTree e comparação com árvores de decisão do scikit learn

Naturalmente, me deparei com uma implementação de árvore de decisão scikit-learn[4]. A implementação sckit-learntem muitas vantagens:

• É rápido e simplificado;
• Escrito no dialeto Cython. Cython compila em código C (que, por sua vez, compila em binário), enquanto ainda interage com o interpretador Python;
• Simples e conveniente;
• Muitas pessoas em ML sabem como trabalhar com modelos scikit-learn. Obtenha ajuda em qualquer lugar graças à sua base de usuários;
• Foi testado em condições de combate (é usado por muitos);
• Simplesmente funciona;
• Ele suporta uma variedade de técnicas de pré e pós-corte [6] e fornece muitos recursos (por exemplo, corte com custo mínimo e pesos de amostra);
• Suporta renderização básica [7].

No entanto, certamente tem algumas desvantagens:

• Não é trivial mudar, em parte por causa do dialeto bastante incomum de Cython (veja as vantagens acima);
• Não há como levar em consideração o conhecimento do usuário sobre a área de assunto ou alterar o processo de aprendizagem;
• A visualização é bastante minimalista;
• Sem suporte para recursos categóricos;
• Sem suporte para valores ausentes;
• A interface para acessar os nós e atravessar a árvore é complicada e não intuitiva;
• Sem suporte para valores ausentes;
• Apenas partições binárias (veja abaixo);
• Não há partições multivariadas (veja abaixo).

Recursos HDTree

O HDTree oferece uma solução para a maioria desses problemas, mas sacrifica muitos dos benefícios da implementação do scikit-learn. Voltaremos a esses pontos mais tarde, então não se preocupe se você ainda não entendeu toda a lista a seguir:

• Interage com o comportamento de aprendizagem;
• Os componentes principais são modulares e fáceis de estender (implementar uma interface);
• Escrito em Python puro (mais disponível)
• Possui rica visualização;
• Suporta dados categóricos;
• Suporta valores ausentes;
• Suporta divisão multivariada;
• Possui uma interface conveniente para navegar na estrutura da árvore;
• Suporta particionamento n-ário (mais de 2 nós filhos);
• Representações textuais da solução;
• Encoraja a explicabilidade imprimindo texto legível por humanos.

Desvantagens:

• Lento;
• Não testado em batalhas;
• A qualidade do software é medíocre;
• Não há muitas opções de cultivo. A implementação suporta alguns parâmetros básicos.

Não há muitas desvantagens, mas são críticas. Vamos ser claros de imediato: não alimente big data para essa implementação. Você vai esperar para sempre. Não o use em um ambiente de produção. Ele pode quebrar inesperadamente. Voce foi avisado! Alguns dos problemas acima podem ser resolvidos com o tempo. No entanto, a taxa de aprendizagem provavelmente permanecerá baixa (embora a inferência seja válida). Você precisará encontrar uma solução melhor para corrigir isso. Eu convido você a contribuir. No entanto, quais são as aplicações possíveis?

• Extração de conhecimento de dados;
• Verificar a visão intuitiva dos dados;
• Compreender o funcionamento interno das árvores de decisão;
• Explore relações causais alternativas em relação ao seu problema de aprendizagem;
• Use como parte de algoritmos mais complexos;
• Criação de relatórios e visualização;
• Use para quaisquer fins de pesquisa;
• Como uma plataforma acessível para testar facilmente suas ideias para algoritmos de árvore de decisão.

Estrutura da árvore de decisão

Embora as árvores de decisão não sejam abordadas em detalhes neste artigo, resumiremos seus blocos de construção básicos. Isso fornecerá uma base para a compreensão dos exemplos posteriormente e também destacará alguns dos recursos do HDTree. A figura a seguir mostra a saída real do HDTree (excluindo marcadores).







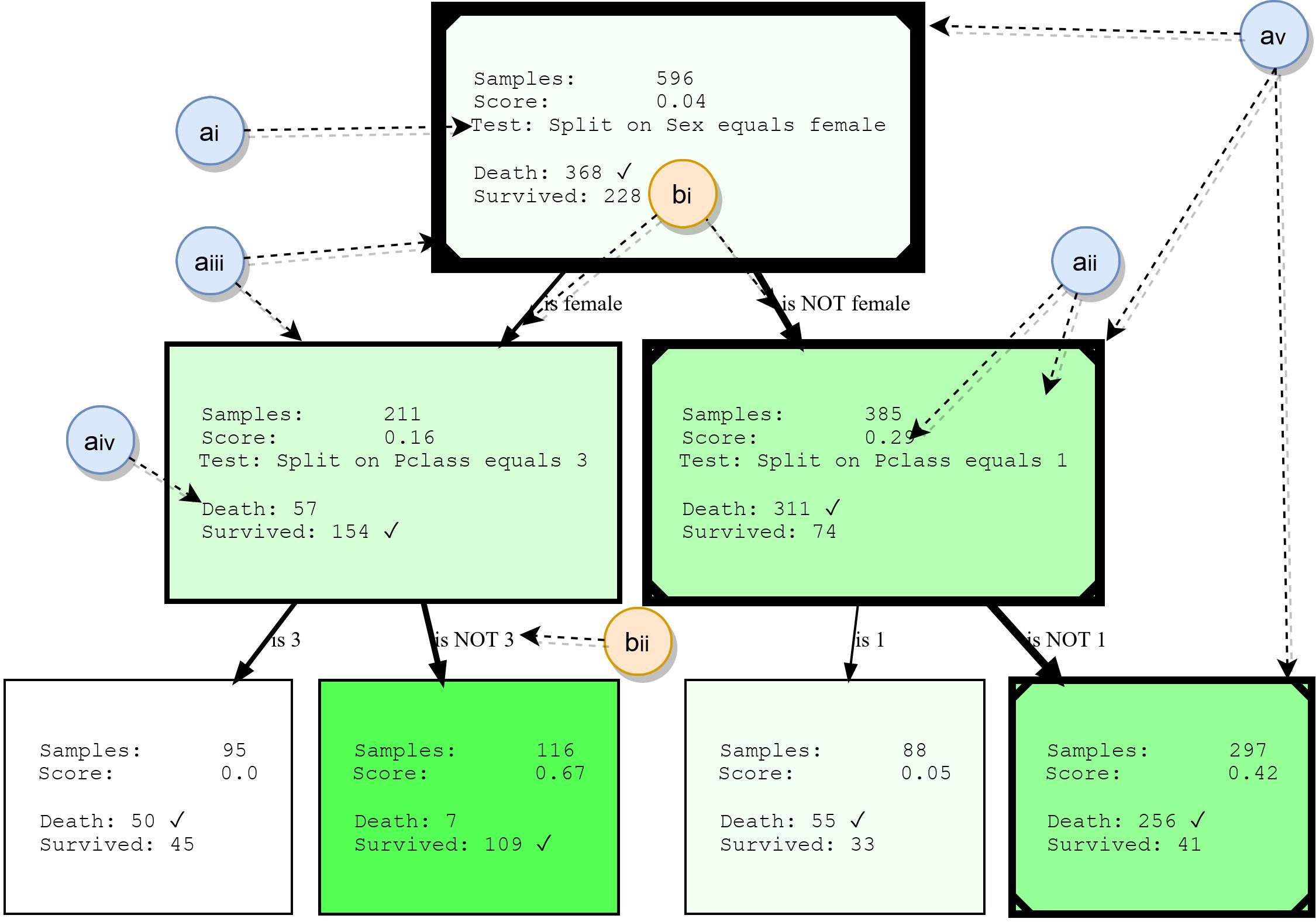
Nós

• ai: , . . * * . . 3.
• aii: , , , , . , . . , ( , .. ). HDTree.
• aiii: A borda dos nós indica quantos pontos de dados passam por este nó. Quanto mais espessa a borda, mais dados fluem pelo nó.
• aiv: lista de destinos de predição e rótulos que possuem pontos de dados passando por este nó. A classe mais comum é marcada.
• av: opcionalmente, a visualização pode marcar o caminho que os pontos de dados individuais seguem (ilustrando a decisão que é tomada quando o ponto de dados atravessa a árvore). Isso é marcado com uma linha no canto da árvore de decisão.

Costelas

• bi: uma seta conecta cada resultado de divisão possível (ai) a seus nós filhos. Quanto mais dados relativos ao pai "fluir" em torno da borda, mais espesso será exibido.
• bii: cada borda possui uma representação textual legível do resultado da divisão correspondente.

De onde vêm as diferentes separações de conjuntos e testes?

Neste ponto, você já deve estar se perguntando como HDTree difere de uma árvore scikit-learn(ou qualquer outra implementação) e por que podemos querer diferentes tipos de partições? Vamos tentar esclarecer isso. Talvez você tenha uma compreensão intuitiva do espaço de recursos . Todos os dados com os quais trabalhamos estão em um determinado espaço multidimensional, que é determinado pelo número e tipo de recursos em seus dados. A tarefa do algoritmo de classificação agora é dividir este espaço em áreas não sobrepostas e atribuiressas áreas são de classe. Vamos visualizar isso. Como nossos cérebros têm dificuldade em mexer com alta dimensionalidade, vamos ficar com um exemplo 2D e um problema muito simples de duas classes, como este:







Você vê um conjunto de dados muito simples composto de duas dimensões (características / atributos) e duas classes. Os pontos de dados gerados foram normalmente distribuídos no centro. Uma rua que é apenas uma função linear  f(x) = ysepara as duas classes: Classe 1 (canto inferior direito) e Classe 2 (canto superior esquerdo). Algum ruído aleatório também foi adicionado (pontos de dados azuis em laranja e vice-versa) para ilustrar os efeitos do overfitting posteriormente. O trabalho de um algoritmo de classificação como o HDTree (embora também possa ser usado para problemas de regressão ) é descobrir a qual classe cada ponto de dados pertence. Em outras palavras, dado um par de coordenadas (x, y)como(6, 2)... O objetivo é descobrir se esta coordenada pertence à classe laranja 1 ou classe azul 2. O modelo discriminante tentará dividir o espaço do objeto (aqui são os eixos (x, y)) em territórios azul e laranja, respectivamente.

Com esses dados, a decisão (regras) sobre como os dados serão classificados parece muito simples. Uma pessoa razoável diria "pense por si mesmo primeiro."

"Esta é a classe 1 se x> y, caso contrário, classe 2." A função y=xpontilhada criará uma separação perfeita . De fato, um classificador de margem máxima, como máquinas de vetores de suporte [8], sugeriria uma solução semelhante. Mas vamos ver quais árvores de decisão resolvem a questão de maneira diferente:







A imagem mostra as áreas onde uma árvore de decisão padrão com profundidade crescente classifica um ponto de dados como classe 1 (laranja) ou classe 2 (azul).

Uma árvore de decisão aproxima uma função linear usando uma função degrau.

Isso se deve ao tipo de validação e regra de particionamento que as árvores de decisão usam. Todos eles funcionam em um padrão  attribute < thresholdque resultará em hiperplanos paralelos aos eixos . No espaço 2D, os retângulos são "cortados". Em 3D, seriam cubóides e assim por diante. Além disso, a árvore de decisão começa a modelar o ruído nos dados quando já existem 8 níveis, ou seja, ocorre overfitting. No entanto, ele nunca encontra uma boa aproximação para uma função linear real. Para verificar isso, usei uma divisão típica de 2 para 1 de dados de treinamento e teste e calculei a precisão das árvores. É 93,84%, 93,03%, 90,81% para o conjunto de teste e 94,54%, 96,57%, 98,81% para o conjunto de treinamento(ordenado pela profundidade da árvore 4, 8, 16). Enquanto a precisão no teste diminui , a precisão do treinamento aumenta .

Um aumento na eficiência do treinamento e uma diminuição nos resultados dos testes é um sinal de overtraining.

As árvores de decisão resultantes são bastante complexas para uma função tão simples. O mais simples (profundidade 4) renderizado com scikit learn já se parece com isto:







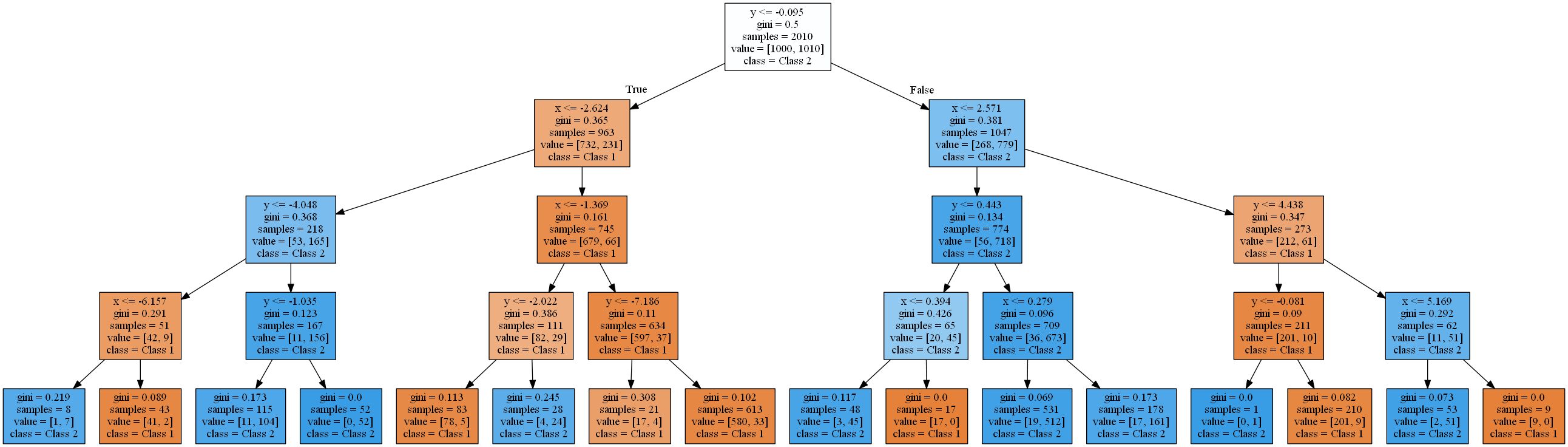
Vou livrar você das árvores mais difícil. Na próxima seção, começaremos resolvendo esse problema usando o pacote HDTree. O HDTree permitirá ao usuário aplicar o conhecimento sobre os dados (assim como o conhecimento sobre separação linear no exemplo). Também permitirá que você encontre soluções alternativas para o problema.

Aplicação do pacote HDTree

Esta seção irá apresentá-lo aos fundamentos do HDTree. Vou tentar tocar em algumas partes de sua API. Sinta-se à vontade para perguntar nos comentários ou entre em contato se tiver alguma dúvida sobre isso. Terei todo o gosto em responder e, se necessário, complementar o artigo. Instalar HDTree é um pouco mais complicado do que pip install hdtree. Desculpe. Primeiro você precisa do Python 3.5 ou mais recente.

• Crie um diretório vazio e dentro dele uma pasta chamada hdtree ( your_folder/hdtree)
• Clone o repositório no diretório hdtree (não em outro subdiretório).
• Instalar as dependências necessárias: numpy, pandas, graphviz, sklearn.
• Adicionar your_foldera PYTHONPATH. Isso incluirá o diretório no mecanismo de importação do Python. Você poderá usá-lo como um pacote Python normal.

Como alternativa, adicione hdtreeà site-packagessua pasta de instalação python. Posso adicionar o arquivo de instalação mais tarde. No momento da escrita, o código não está disponível no repositório pip. Todo o código que gera os gráficos e a saída abaixo (assim como mostrado anteriormente) está no repositório e é postado diretamente aqui . Resolvendo um problema linear com uma árvore irmã



Vamos começar imediatamente com o código:

from hdtree import HDTreeClassifier, SmallerThanSplit, EntropyMeasure
hdtree_linear = HDTreeClassifier(allowed_splits=[SmallerThanSplit.build()], # Split rule in form a < b
    information_measure=EntropyMeasure(), # Use Information Gain for the scores attribute_names=['x', 'y' ]) # give the
    attributes some interpretable names # standard sklearn-like interface hdtree_linear.fit(X_street_train,
    y_street_train) # create tree graph hdtree_linear.generate_dot_graph()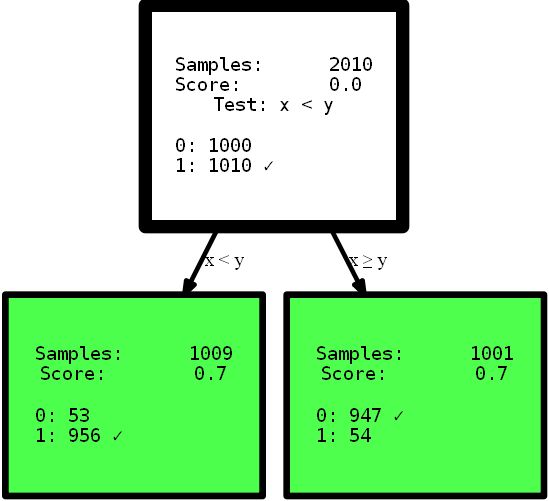 

Sim, a árvore resultante tem apenas um nível de altura e oferece a solução perfeita para esse problema. Este é um exemplo artificial para mostrar o efeito. No entanto, espero que fique mais claro: tenha uma visão intuitiva dos dados, ou simplesmente forneça uma árvore de decisão com diferentes opções para dividir o espaço de recursos, o que pode oferecer uma solução mais simples e às vezes até mais precisa . Imagine que você precise interpretar as regras das árvores apresentadas aqui para encontrar informações úteis. Qual interpretação você pode entender primeiro e em qual você confia mais? Uma interpretação complexa usando funções de várias etapas ou uma pequena árvore precisa? Acho que a resposta é bem simples. Mas vamos mergulhar um pouco mais fundo no próprio código. Ao inicializar, o HDTreeClassifiermais importante que você deve fornecer é allowed_splits. Aqui você fornece uma lista contendo as regras de particionamento possíveis que o algoritmo tenta durante o treinamento para cada nó para encontrar um bom particionamento local dos dados. Neste caso, fornecemos exclusivamente  SmallerThanSplit. Essa divisão faz exatamente o que você vê: pega dois atributos (tenta qualquer combinação) e divide os dados de acordo com o esquema a_i < a_j. Que (não muito aleatoriamente) corresponde aos nossos dados da melhor forma possível.



Este tipo de divisão é conhecido como divisão multivariadaIsso significa que a separação usa mais de um recurso para tomar uma decisão. Não é como o particionamento unilateral usado na maioria das outras árvores, como scikit-tree(veja os detalhes acima) que leva exatamente um atributo em consideração . Claro, ele HDTreetambém tem opções para obter o "particionamento normal", como nas árvores do scikit - a família QuantileSplit. Vou mostrar mais à medida que o artigo avança. Outra coisa desconhecida que você pode ver no código é o hiperparâmetro information_measure. O parâmetro representa uma dimensão que é usada para avaliar o valor de um único nó ou uma divisão completa (nó pai com seus nós filhos). A opção escolhida é baseada na entropia [10]. Você também pode ter ouvido falar deo coeficiente de Gini , que seria outra opção válida. Claro, você pode fornecer sua própria dimensão simplesmente implementando a interface apropriada. Se desejar, implemente um índice gini , que pode ser usado na árvore sem reimplementar mais nada. Basta copiar EntropyMeasure()e adaptar para você. Vamos nos aprofundar no desastre do Titanic . Amo aprender com meus próprios exemplos. Agora você verá mais algumas funções do HDTree com um exemplo específico, não nos dados gerados.

Conjunto de dados

Estaremos trabalhando com o famoso conjunto de dados de aprendizado de máquina para o curso de jovens lutadores: o conjunto de dados de desastre do Titanic. Este é um conjunto bastante simples, que não é muito grande, mas contém vários tipos de dados diferentes e valores ausentes, embora não seja completamente trivial. Além disso, é compreensível para os humanos e muitas pessoas já trabalharam com ele. Os dados têm a seguinte aparência:







Você pode ver que existem todos os tipos de atributos. Tipos numéricos, categóricos, inteiros e até mesmo valores ausentes (veja a coluna Cabine). O desafio é prever se um passageiro sobreviveu ao desastre do Titanic com base nas informações disponíveis sobre os passageiros. Você pode encontrar uma descrição dos atributos de valor aqui . Ao estudar tutoriais de ML e aplicar este conjunto de dados, você está fazendo todos os tipos depré - processamento para poder trabalhar com modelos de aprendizado de máquina comuns, por exemplo, removendo valores ausentes NaNsubstituindo valores [12], descartando linhas / colunas, codificação unitária [13] de dados categóricos (por exemplo, Embarkede / Sexou agrupando dados para obter um conjunto de dados válido que aceita o modelo ML. Este tipo de limpeza não é tecnicamente exigido pelo HDTree. Você pode fornecer os dados como estão e o modelo aceitará com prazer. Altere os dados apenas ao projetar objetos reais. Simplifiquei tudo para começar.

Treinando o primeiro HDTree em dados do Titanic

Vamos apenas pegar os dados como estão e alimentar o modelo. O código básico é semelhante ao código acima, mas este exemplo permitirá muito mais divisões de dados.

    hdtree_titanic = HDTreeClassifier(allowed_splits=[FixedValueSplit.build(), # e.g., Embarked = 'C'
    SingleCategorySplit.build(), # e.g., Embarked -> ['C', 'Q', 'S']
    TwentyQuantileRangeSplit.build(), # e.g., IN Quantile 3-5
    TwentyQuantileSplit.build()], # e.g., BELOW Quantile 7
    information_measure=EntropyMeasure(),
    attribute_names=col_names,
    max_levels=3) # restrict to grow to a max of 3 levels
    hdtree_titanic.fit(X_titanic_train.values, y_titanic_train.values)
    hdtree_titanic.generate_dot_graph()
    

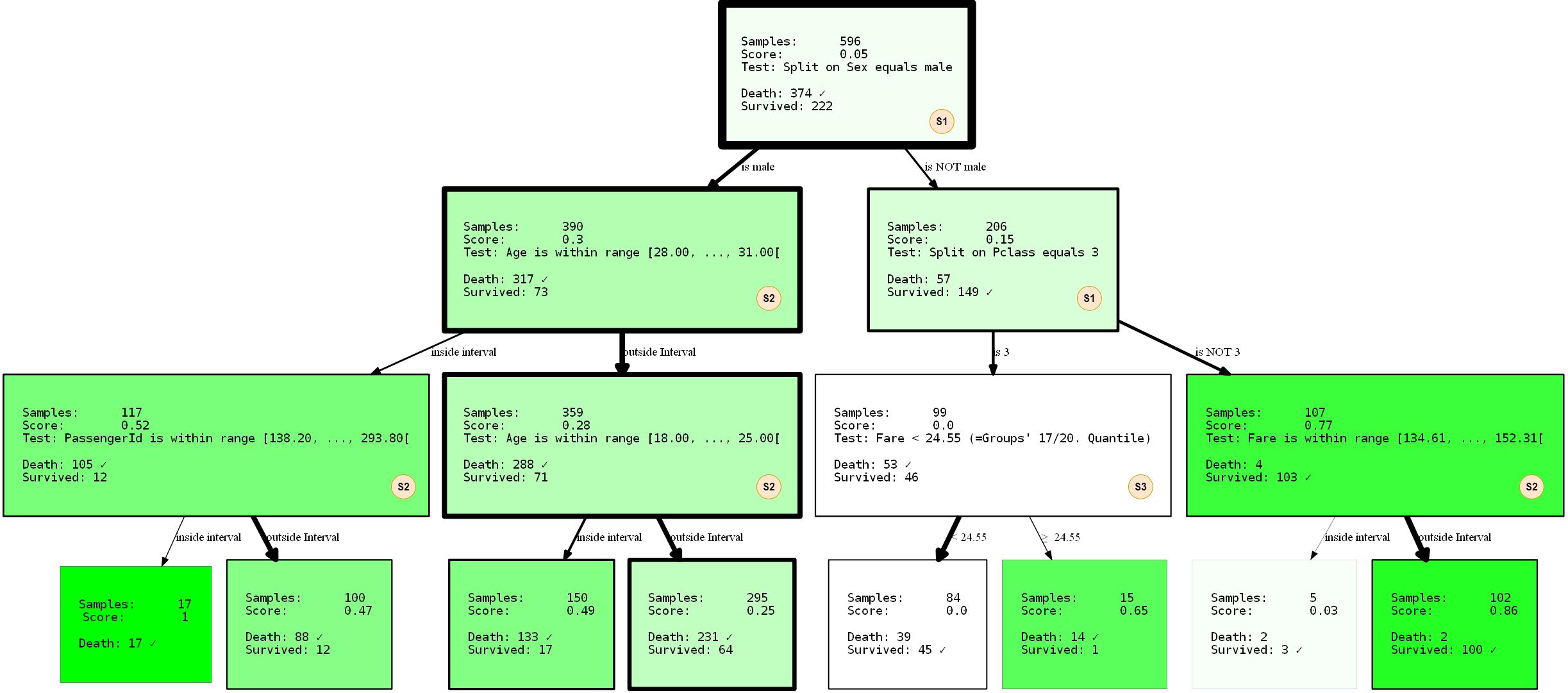
Vamos dar uma olhada mais de perto no que está acontecendo. Criamos uma árvore de decisão com três níveis, que escolhemos usar 3 de 4 SplitRules possíveis . Eles são marcados com as letras S1, S2, S3. Vou explicar brevemente o que eles fazem.

• O S1: FixedValueSplit. Essa divisão trabalha com dados categóricos e escolhe um dos valores possíveis. Os dados são então divididos em uma parte que tem esse valor e outra parte que não tem nenhum valor definido. Por exemplo, PClass = 1 e Pclass ≠ 1 .
• S2: () QuantileRangeSplit. . , . 1 5 . ( ) (measure_information). (i) (ii) — . .
• S3: (Vinte) QuantileSplit. Semelhante a Split Range (S2), mas divide os dados por limite. Isso é basicamente o que as árvores de decisão regulares fazem, exceto que geralmente tentam todos os limites possíveis em vez de um número fixo.

Você deve ter percebido que não está SingleCategorySplitenvolvido. Aproveito para esclarecer de qualquer maneira, pois a omissão dessa divisão surgirá posteriormente:

• S4: SingleCategorySplitFuncionará de forma semelhante FixedValueSplit, mas criará um nó filho para cada valor possível, por exemplo: para o atributo PClass serão 3 nós filhos (cada um para Classe 1, Classe 2 e Classe 3 ). Observe que FixedValueSplité idêntico SingleValueSplitse houver apenas duas categorias possíveis.

As divisões individuais são um tanto "inteligentes" com respeito aos tipos / valores de dados que "aceitam". Até alguma extensão, eles sabem em que circunstâncias se aplicam e não se aplicam. A árvore também foi treinada com uma divisão de 2 para 1 dos dados de treinamento e teste.O desempenho foi de 80,37% de precisão nos dados de treinamento e 81,69 nos dados de teste. Não é tão ruim.

Limitando divisões

Vamos supor que você não esteja muito satisfeito com as soluções encontradas por algum motivo. Talvez você decida que a primeira divisão no topo da árvore é muito trivial (divisão por atributo sex). HDTree resolve o problema. A solução mais simples seria evitar FixedValueSplit(e, nesse caso, o equivalente SingleCategorySplit) de aparecer no topo. É muito simples. Altere a inicialização das divisões desta forma:

    - SNIP -
    ...allowed_splits=[FixedValueSplit.build_with_restrictions(min_level=1),
    SingleCategorySplit.build_with_restrictions(min_level=1),...],
    - SNIP -

Apresentarei o HDTree resultante em sua totalidade, uma vez que podemos observar a divisão ausente (S4) dentro da árvore recém-gerada.







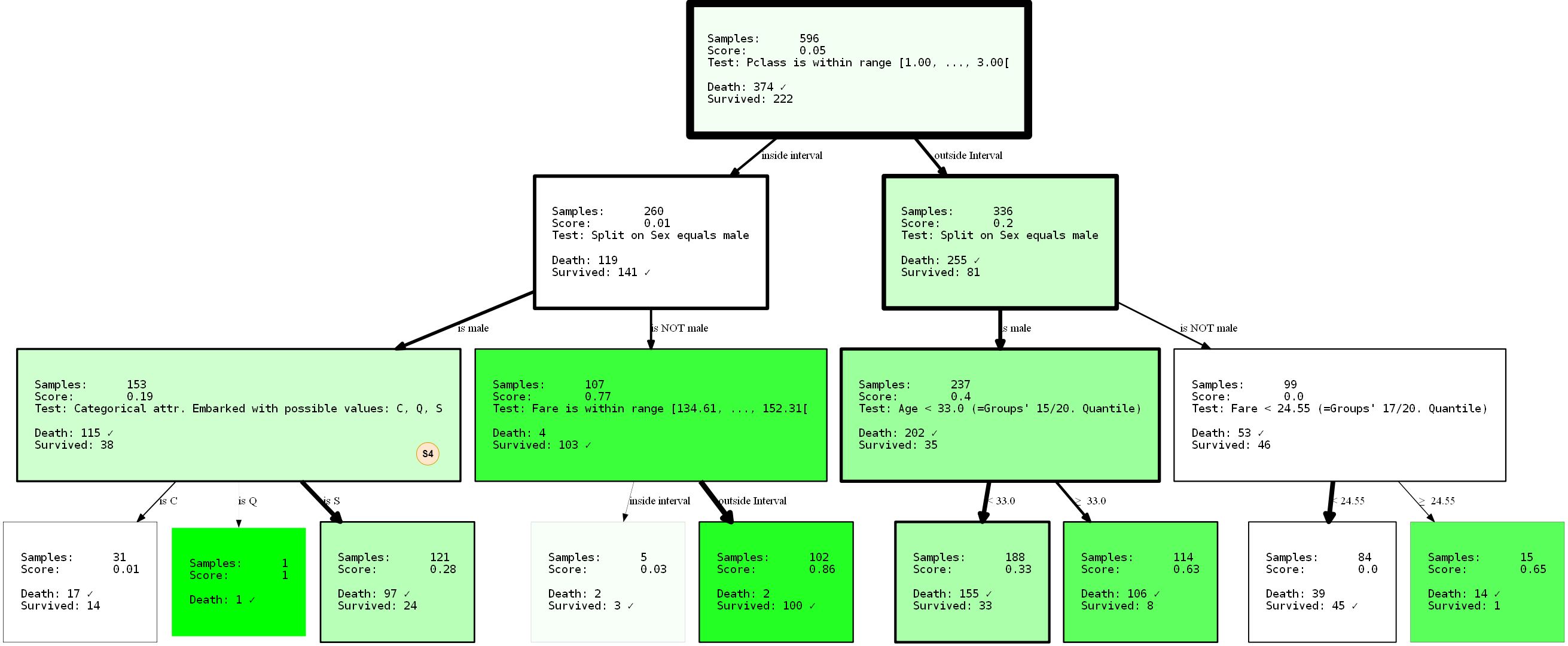
Ao evitar que a divisão sexapareça na raiz graças ao parâmetro  min_level=1(dica: é claro que você também pode fornecer max_level), reestruturamos completamente a árvore. Seu desempenho agora é de 80,37% e 81,69% (treinamento / teste). Não mudou nada, mesmo que realizássemos a separação supostamente melhor no nó raiz.

Como as árvores de decisão são gananciosas, elas encontrarão apenas a _ melhor partição local para cada nó, que não é necessariamente a _ melhor _ opção. Na verdade, encontrar uma solução ideal para um problema de árvore de decisão é um problema NP-completo, como foi provado em [15].

Portanto, o melhor que podemos pedir são heurísticas. Vamos voltar ao exemplo: perceber que já temos uma representação não trivial dos dados? Porém, é trivial. dizer que os homens terão apenas uma baixa chance de sobrevivência, em menor medida, pode-se concluir que ser uma pessoa de primeiro ou segundo grau PClassvoando para fora de Cherbourg ( Embarked=C) pode aumentar suas chances de sobrevivência. Ou se você for um homem com  PClass 3menos de 33 anos, suas chances também aumentam? Lembre-se: mulheres e crianças primeiro. É um bom exercício tirar essas conclusões por si mesmo, interpretando a visualização. Essas conclusões só foram possíveis devido à limitação da árvore. Quem sabe o que mais pode ser revelado aplicando outras restrições? Tente!



Como um exemplo final desse tipo, quero mostrar como restringir a partição a atributos específicos. Isso é aplicável não apenas para evitar o aprendizado da árvore em correlações indesejadas ou alternativas forçadas , mas também restringe o espaço de pesquisa. A abordagem pode reduzir drasticamente o tempo de execução, especialmente ao usar particionamento multivariável. Se você voltar ao exemplo anterior, poderá encontrar um nó que verifica um atributo PassengerId. Talvez não queiramos modelá-lo, pois pelo menos não deve contribuir com informações sobre sobrevivência. Verificar a identificação do passageiro pode ser um sinal de overtraining. Vamos mudar a situação com um parâmetro blacklist_attribute_indices.

    - SNIP -
    ...allowed_splits=[TwentyQuantileRangeSplit.build_with_restrictions(blacklist_attribute_indices=['PassengerId']),
    FixedValueSplit.build_with_restrictions(blacklist_attribute_indices=['Name Length']),
    ...],
    - SNIP -
    

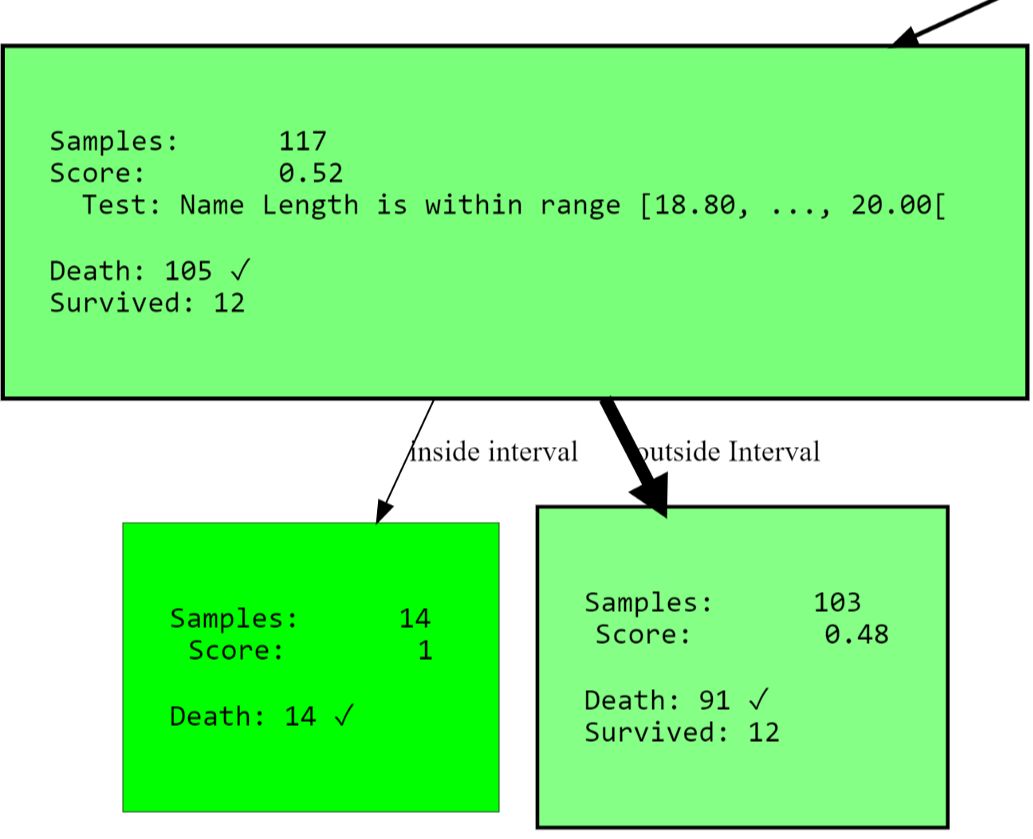
Você pode perguntar por que name lengthele aparece. Esteja ciente de que nomes longos (nomes duplos ou títulos [nobres]) podem indicar um passado rico, aumentando suas chances de sobrevivência.

Dica adicional: você sempre pode adicionar a mesma coisa  SplitRuleduas vezes. Se você quiser apenas colocar um atributo na lista negra para certos níveis de HDTree, basta adicionar SplitRulenenhum limite de nível.

Previsão de ponto de dados

Como você já deve ter notado, a interface genérica scikit-learn pode ser usada para predição. Este predict(), predict_proba()bem  score(). Mas você pode ir mais longe. Existe explain_decision()um que irá exibir uma representação textual da solução.

print(hdtree_titanic_3.explain_decision(X_titanic_train[42]))

Supõe-se que esta seja a última alteração na árvore. O código irá gerar isto:

Query:
Query: 
 {'PassengerId': 273, 'Pclass': 2, 'Sex': 'female', 'Age': 41.0, 'SibSp': 0, 'Parch': 1, 'Fare': 19.5, 'Cabin': nan, 'Embarked': 'S', 'Name Length': 41}

Predicted sample as "Survived" because of: 
Explanation 1:
Step 1: Sex doesn't match value male
Step 2: Pclass doesn't match value 3
Step 3: Fare is OUTSIDE range [134.61, ..., 152.31[(19.50 is below range)
Step 4: Leaf. Vote for {'Survived'}
    

Isso funciona mesmo para dados ausentes. Vamos definir o índice de atributo 2 ( Sex) como ausente (None):

    passenger_42 = X_titanic_train[42].copy()
    passenger_42[2] = None
    print(hdtree_titanic_3.explain_decision(passenger_42))
    

Query: 
 {'PassengerId': 273, 'Pclass': 2, 'Sex': None, 'Age': 41.0, 'SibSp': 0, 'Parch': 1, 'Fare': 19.5, 'Cabin': nan, 'Embarked': 'S', 'Name Length': 41}

Predicted sample as "Death" because of: 
Explanation 1:
Step 1: Sex has no value available
Step 2: Age is OUTSIDE range [28.00, ..., 31.00[(41.00 is above range)
Step 3: Age is OUTSIDE range [18.00, ..., 25.00[(41.00 is above range)
Step 4: Leaf. Vote for {'Death'}
---------------------------------
Explanation 2:
Step 1: Sex has no value available
Step 2: Pclass doesn't match value 3
Step 3: Fare is OUTSIDE range [134.61, ..., 152.31[(19.50 is below range)
Step 4: Leaf. Vote for {'Survived'}
---------------------------------
    

Isso imprimirá todos os caminhos de decisão (há mais de um, porque em alguns nós a decisão não pode ser feita!). O resultado final será a classe mais comum de todas as folhas.

... outras coisas úteis

Você pode ir em frente e obter a visualização em árvore como texto:

    Level 0, ROOT: Node having 596 samples and 2 children with split rule "Split on Sex equals male" (Split Score:
    0.251)
    -Level 1, Child #1: Node having 390 samples and 2 children with split rule "Age is within range [28.00, ..., 31.00["
    (Split Score: 0.342)
    --Level 2, Child #1: Node having 117 samples and 2 children with split rule "Name Length is within range [18.80,
    ..., 20.00[" (Split Score: 0.543)
    ---Level 3, Child #1: Node having 14 samples and no children with
    - SNIP -
    

Ou acesse todos os nós limpos (com uma pontuação alta):

    [str(node) for node in hdtree_titanic_3.get_clean_nodes(min_score=0.5)]
    

    ['Node having 117 samples and 2 children with split rule "Name Length is within range [18.80, ..., 20.00[" (Split
    Score: 0.543)',
    'Node having 14 samples and no children with split rule "no split rule" (Node Score: 1)',
    'Node having 15 samples and no children with split rule "no split rule" (Node Score: 0.647)',
    'Node having 107 samples and 2 children with split rule "Fare is within range [134.61, ..., 152.31[" (Split Score:
    0.822)',
    'Node having 102 samples and no children with split rule "no split rule" (Node Score: 0.861)']
    

Extensão HDTree

A coisa mais significativa que você pode querer adicionar ao sistema é a sua própria SplitRule. A regra de separação pode realmente fazer o que quiser separar ... Implementar SplitRulepor meio da implementação AbstractSplitRule. Isso é um pouco complicado, pois você tem que lidar com a ingestão de dados, avaliação de desempenho e tudo isso sozinho. Por essas razões, existem mixins no pacote que você pode adicionar à implementação dependendo do tipo de divisão. Os mixins fazem a maior parte da parte difícil para você.

Descubra os detalhes de como obter uma profissão de alto perfil do zero ou Subir de nível em habilidades e salários, fazendo cursos online SkillFactory:

• Curso de aprendizado de máquina (12 semanas)
• Curso avançado "Aprendizado de máquina Pro + Aprendizado profundo" (20 semanas)
• « Machine Learning Data Science» (20 )
• «Python -» (9 )

E

• Data Science (12 )
• - (8 )
• (9 )
• DevOps (12 )
• Java- (18 )
• JavaScript (12 )
• UX- (9 )
• Web- (7 )