Estrutura matemática de colisões de partículas elementares

Os físicos descobriram a estrutura algébrica subjacente à intrincada matemática das colisões de partículas. Alguns esperam que isso nos leve a uma teoria mais elegante do mundo físico.

Quando os físicos de partículas tentam modelar experimentos, eles se deparam com cálculos impossíveis devido a uma equação infinitamente grande que está além do alcance da matemática moderna.



Felizmente, eles podem fazer previsões geralmente precisas sem trabalhar toda essa matemática enigmática até o fim. Encurtando os cálculos, os cientistas do Large Hadron Collider no CERN, na Europa, fazem previsões que coincidem com os eventos que eles observam em colisões de partículas subatômicas que varrem a uma velocidade tremenda ao longo de uma pista de 26 quilômetros.



Infelizmente, a era do acordo entre previsão e observação pode estar chegando ao fim. Quanto mais precisas as medições se tornam, mais difícil é para os esquemas de computação aproximados usados ​​pelos teóricos se manterem atualizados.



“Já estamos perto de exaurir os fundos que temos”, disse Claude Dar , físico de partículas do CERN.



No entanto, três trabalhos recentes de Pierpaolo Mastrolia, da Universidade de Pádua, na Itália, e de Sebastian Mizerado Princeton Institute for Advanced Study em New Jersey descobriu a estrutura matemática por trás dessas equações. Ele fornece uma nova maneira de reduzir um número infinito de membros a uma dúzia de componentes necessários. O método deles pode ajudar a levar a precisão da previsão para o próximo nível que os teóricos precisam para ir além do modelo principal, mas incompleto da física de partículas.



“Eles mostraram muitos resultados que comprovam a viabilidade desta técnica promissora”, disse Dar.



No entanto, os benefícios podem ser muito maiores do que simplesmente melhorar as previsões. O novo método contorna a matemática entediante tradicional calculando diretamente os "números de interseção", que alguns acreditam que pode nos dar uma descrição mais elegante do mundo subatômico.



“Não é apenas matemática”, disse Simon Caron-Hewot, da Universidade McGill, um teórico quântico que estuda as implicações do trabalho de Mastrolius e Mizera. "Está tudo profundamente entrelaçado com a teoria quântica de campos."

Loop infinito

Ao simular colisões de partículas, os físicos usam diagramas de Feynman , uma notação simples inventada por Richard Feynman nos anos 1940.



Para entender como essa gravação funciona, considere um evento simples: dois quarks se aproximam, trocam um glúon no processo de "colisão" e, em seguida, ricocheteiam um no outro ao longo de trajetórias diferentes.



No diagrama de Feynman, os caminhos dos quarks são denotados por “pernas”, que formam “topos” na junção durante a interação das partículas. Feynman desenvolveu regras para transformar tal imagem em equações que calculam a probabilidade da ocorrência desse evento. Você escreve uma função específica para cada perna e vértice - geralmente uma fração usando a massa e o momento da partícula - e multiplica tudo. Para opções simples como a nossa, os cálculos podem caber em um guardanapo.





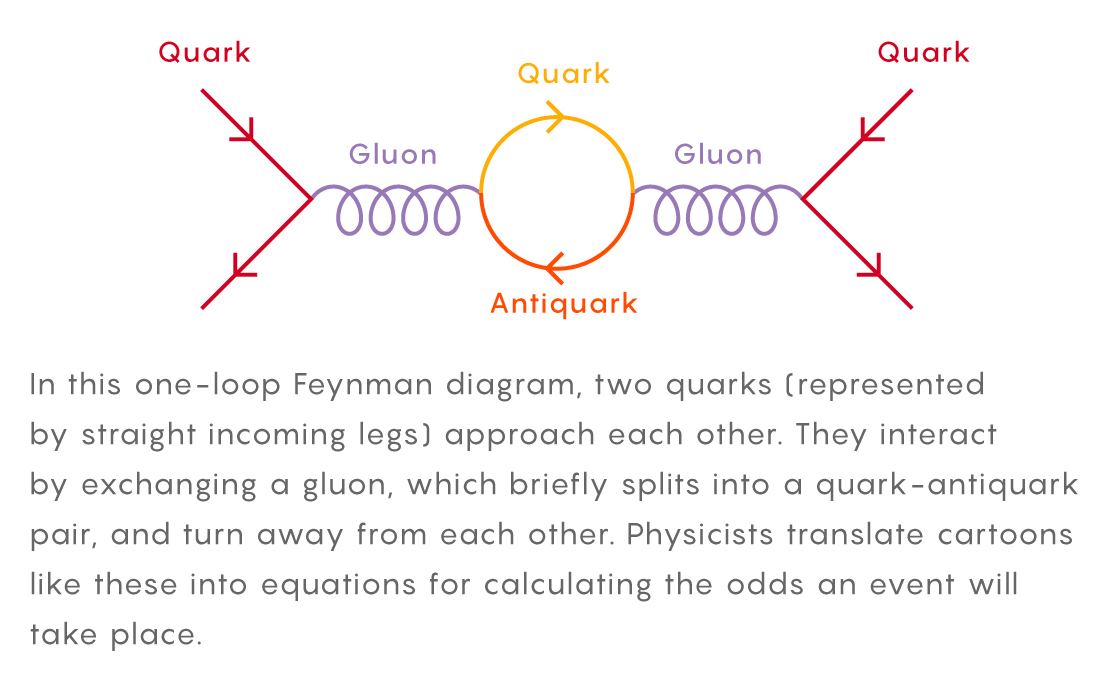
Neste diagrama, dois quarks (indicados por pernas retas com setas apontando para dentro) se aproximam de um loop. Eles interagem, trocando glúons, que por um curto período de tempo se dividem em um par quark-antiquark, e então se separam. Os físicos traduzem esses padrões em equações que calculam a probabilidade da ocorrência desse evento.



No entanto, a regra de ouro da teoria quântica é considerar todas as possibilidades, e a troca de um glúon simples é apenas um da vasta variedade de cenários que podem ocorrer quando dois quarks colidem. O glúon que as partículas trocam pode se dividir em um par quark-antiquark por um curto período de tempo e depois voltar a ser um glúon. Dois quarks se encontram e dois quarks divergem, mas muito pode acontecer entre eles. Para explicar completamente o que está acontecendo, dando uma previsão ideal, você precisará desenhar um número infinito de diagramas. Ninguém espera resultados perfeitos, mas a chave para melhorar a precisão dos cálculos é ir o mais longe possível ao longo da cadeia infinita de eventos.



E é aqui que os físicos ficam presos.



Para estudar esse centro oculto com mais detalhes, você precisa recorrer às partículas virtuais - flutuações quânticas que afetam gradualmente o resultado de cada interação. A existência de curto prazo do par de quarks mencionado acima, como muitos eventos virtuais, é indicada no diagrama de Feynman por um loop fechado. Os loops confundem os físicos - são caixas pretas que adicionam camadas extras a cenários infinitos. Para calcular de alguma forma as possibilidades implícitas no loop, os teóricos precisam obter integrais. Essas integrais atingem proporções monstruosas nos diagramas de Feynman com muitos loops que aparecem à medida que os pesquisadores avançam na cadeia de eventos e são responsáveis ​​por interações virtuais cada vez mais complexas.



Os físicos têm algoritmos para calcular as probabilidades de cenários sem loops ou com um loop, mas já as colisões com dois loops colocam os computadores de joelhos. Este é o teto para a precisão preditiva - e para os físicos entenderem as implicações da teoria quântica.







No entanto, tudo isso tem um lado positivo: os físicos não precisam calcular absolutamente todas as integrais de um diagrama de Feynman complexo, uma vez que a maioria deles pode ser reunida em um.



Milhares de integrais podem ser reduzidos a várias dezenas de "básicos", que podem ser pesados ​​e adicionados. Mas quais integrais podem ser coletadas em outras básicas separadas é uma questão computacional difícil. Os pesquisadores usam computadores que essencialmente fazem suposições com base em milhões de interações e têm dificuldade em derivar combinações significativas de integrais.



No entanto, graças aos números de interseção, os físicos podem ter encontrado uma maneira de selecionar elegantemente informações importantes de cálculos extensos de integrais de Feynman.

Impressão digital geométrica

O trabalho de Mastrolia e Mizera surge de um ramo da matemática como a topologia algébrica , que classifica formas e espaços. Ajuda nestas teorias de " cohomologia ", permitindo calcular "impressões digitais" algébricas a partir de espaços geométricos complexos.



"É como uma sinopse, um dispositivo algébrico que captura a essência do espaço que você está explorando", disse Clement Dupont, matemático da Universidade de Montpellier, na França.



Os diagramas de Feynman podem ser traduzidos em espaços geométricos, que podem então ser analisados ​​usando cohomologia. Cada ponto nesse espaço pode representar um dos muitos cenários que se desdobram quando as partículas colidem.



Podemos esperar que, tomando a cohomologia deste espaço - encontrando sua estrutura algébrica - você possa calcular os pesos para as integrais fundamentais. No entanto, o espaço geométrico que caracteriza a maioria dos diagramas de Feynman é tão curvo que resiste a muitos cálculos cohomológicos.



Em 2017, Mizera estava tentando analisar colisões de objetos na teoria das cordas quando se deparou com ferramentas inventadas pela primeira vez por Israel Gelfand e Katsuhiko Aomoto nas décadas de 1970 e 1980, quando eles estavam trabalhando em uma cohomologia chamada cohomologia torcida. Mais tarde naquele mesmo ano, Mizera conheceu Mastrolia, que percebeu que essas técnicas poderiam funcionar no diagrama de Feynman também. No ano passado, eles publicaram três artigos que usaram a teoria da cohomologia para acelerar cálculos de colisões de partículas simples.



Seu método pega uma família de cenários físicos interconectados, apresenta-os como um espaço geométrico e calcula sua cohomologia distorcida. “E essa cohomologia distorcida diz tudo sobre as integrais de interesse para nós”, disse Mizera.



Em particular, a cohomologia torcida informa quantos integrais básicos são necessários e quais devem ser seus pesos. Esses pesos aparecem como valores que eles chamam de "números de interseção". Como resultado, milhares de integrais secam até uma soma ponderada de várias dezenas de integrais.



É possível que as teorias de cohomologia que produzem esses números de interseção possam fazer mais do que tornar o cálculo mais fácil - elas podem nos apontar para a significância física das quantidades mais importantes na computação.



Por exemplo, quando um glúon virtual decai em dois quarks virtuais, sua vida útil pode ser diferente. No espaço geométrico associado a eles, cada ponto pode denotar um tempo de vida de quark diferente. Ao calcular os pesos, os pesquisadores vêem que cenários com as partículas virtuais de vida mais longa - ou seja, aqueles casos em que as partículas se tornam quase reais - influenciam o resultado mais do que outros.



“Isso é o que é incrível com este método”, disse Karon-Hewot. "Ele recria tudo a partir desses eventos raros e especiais."



Na semana passada, Mizera, Mastrolia e seus colegas publicaram outro preprint, onde é mostrado que esta técnica evoluiu o suficiente para trabalhar com diagramas reais com dois loops. No próximo trabalho, Karon-Hewot desenvolverá esse método ainda mais, possivelmente controlando até mesmo diagramas de três loops.



Se for bem-sucedida, essa técnica pode ajudar a abrir uma nova geração de previsões teóricas. E, como alguns pesquisadores suspeitam, pode até nos mostrar uma nova perspectiva da realidade.