Livro "Processamento de linguagem natural em ação"

Olá Habitantes! Publicamos um guia prático para processar e gerar textos em linguagem natural. O livro está equipado com todas as ferramentas e técnicas necessárias para criar sistemas de PNL aplicados a fim de garantir a operação de um assistente virtual (chatbot), um filtro de spam, um programa de moderador de fórum, um analisador de sentimento, um programa de construção de base de conhecimento, um analisador inteligente de texto em linguagem natural ou praticamente qualquer outro aplicativo de PNL que você possa imaginar.



O livro é direcionado a desenvolvedores Python intermediários a avançados. Uma parte significativa do livro será útil para os leitores que já sabem como projetar e desenvolver sistemas complexos, pois contém vários exemplos de soluções recomendadas e revela as capacidades dos algoritmos de PNL mais modernos. Embora o conhecimento de programação orientada a objetos em Python possa ajudá-lo a construir sistemas melhores, não é necessário usar as informações deste livro.

Redes neurais de feedback: redes neurais recorrentes

O Capítulo 7 demonstra as possibilidades de analisar um fragmento ou uma frase inteira usando uma rede neural convolucional, rastreando palavras adjacentes em uma frase aplicando um filtro de pesos compartilhados (realizando convolução) sobre elas. Palavras que ocorrem em grupos também podem ser encontradas em um pacote. A teia também é resistente a pequenas mudanças nas posições dessas palavras. Ao mesmo tempo, conceitos adjacentes podem afetar significativamente a rede. Mas se você precisar dar uma olhada no quadro geral do que está acontecendo, leve em consideração as relações durante um período de tempo mais longo, uma janela que cobre mais de 3-4 tokens do estoque? Como introduzir o conceito de eventos passados ​​na rede? Memória?



Para cada exemplo de treinamento (ou lote de exemplos desordenados) e saída (ou lote de saídas) da rede neural feedforward, os pesos da rede neural precisam ser ajustados para neurônios individuais com base no método de retropropagação. Já demonstramos isso. Mas os resultados da fase de treinamento para o próximo exemplo são principalmente independentes da ordem das entradas. As redes neurais convolucionais tentam capturar essas relações de ordem capturando as relações locais, mas há outra maneira.



Em uma rede neural convolucional, cada exemplo de treinamento é passado para a rede como um conjunto agrupado de tokens de palavras. Os vetores de palavras são agrupados em uma matriz na forma (comprimento do vetor de palavras × número de palavras no exemplo), como mostrado na Fig. 8,1





Mas essa sequência de vetores de palavras pode ser facilmente transmitida para a rede neural feedforward normal do Capítulo 5 (Figura 8.2), certo?





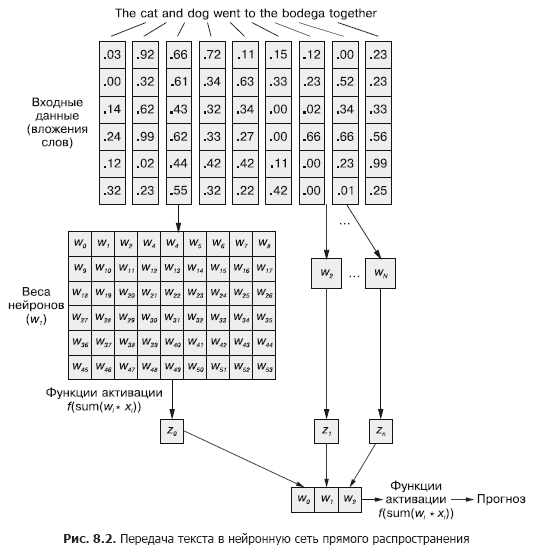
Claro, este é um modelo perfeitamente funcional. Com esse método de transferência de dados de entrada, a rede neural feedforward será capaz de responder a ocorrências conjuntas de tokens, que é o que precisamos. Mas, ao mesmo tempo, ele reagirá a todas as ocorrências conjuntas da mesma maneira, independentemente de estarem separadas por um texto longo ou próximas umas das outras. Além disso, as redes neurais feedforward, como as CNNs, são ruins para lidar com documentos de comprimento variável. Eles não conseguem processar o texto no final do documento se ele ultrapassar a largura da web.



As redes neurais feedforward têm melhor desempenho na modelagem do relacionamento de uma amostra de dados como um todo com seu rótulo correspondente. As palavras no início e no final de uma frase têm exatamente o mesmo efeito no sinal de saída e no meio, apesar do fato de que provavelmente não sejam semanticamente relacionadas entre si.



Essa uniformidade (uniformidade de influência) pode claramente causar problemas no caso de, por exemplo, tokens de negação severa e modificadores (adjetivos e advérbios), como "não" ou "bom". Em uma rede neural feedforward, as palavras de negação afetam o significado de todas as palavras em uma frase, mesmo se estiverem muito distantes do lugar em que deveriam realmente influenciar.



As convoluções unidimensionais são uma maneira de resolver essas relações entre tokens, analisando várias palavras nas janelas. As camadas de redução da resolução discutidas no Capítulo 7 são projetadas especificamente para acomodar pequenas mudanças na ordem das palavras. Neste capítulo, veremos uma abordagem diferente que nos ajudará a dar o primeiro passo em direção ao conceito de memória de rede neural. Em vez de desmontar uma linguagem como um grande bloco de dados, começaremos a examinar sua formação sequencial, token por token, ao longo do tempo.

8,1 Memorização em redes neurais

Claro, as palavras em uma frase raramente são completamente independentes umas das outras; suas ocorrências são influenciadas ou influenciadas por ocorrências de outras palavras no documento. Por exemplo: O carro roubado entrou em alta velocidade na arena e O carro palhaço entrou em alta velocidade na arena.



Você pode ter impressões completamente diferentes das duas frases ao ler até o final. A construção da frase neles é a mesma: adjetivo, substantivo, verbo e frase preposicional. Mas a substituição do adjetivo neles muda radicalmente a essência do que está acontecendo do ponto de vista do leitor.



Como modelar esse relacionamento? Como entender que arena e até mesmo velocidade podem ter conotações ligeiramente diferentes se houver um adjetivo na frente deles na frase que não é uma definição direta de nenhum deles?



Se houvesse uma maneira de lembrar o que aconteceu um momento antes (especialmente lembre-se na etapa t + 1 o que aconteceu na etapa t), seria possível identificar padrões que surgem quando certos tokens aparecem em uma sequência de padrões associados a outros tokens. As redes neurais recorrentes (RNNs) possibilitam que uma rede neural memorize as palavras anteriores de uma sequência.



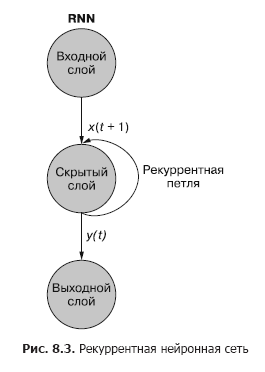
Como você pode ver na fig. 8.3, um neurônio recorrente separado da camada oculta adiciona um loop recorrente à rede para "reutilizar" a saída da camada oculta no tempo t. A saída no tempo t é adicionada à próxima entrada no tempo t + 1. A rede processa essa nova entrada na etapa t + 1 para produzir uma saída da camada oculta no tempo t + 1. Esta saída no tempo t + 1 em seguida, ele é reutilizado pela rede e incluído no sinal de entrada em uma etapa de tempo t + 2, etc.





Embora a ideia de influenciar um estado ao longo do tempo pareça um pouco confusa, o conceito básico é simples. Os resultados de cada sinal na entrada de uma rede neural feedforward convencional em uma etapa de tempo t são usados ​​como um sinal de entrada adicional junto com a próxima parte dos dados alimentados à entrada de rede em uma etapa de tempo t + 1. A rede recebe informações não apenas sobre o que está acontecendo agora, mas também sobre o que aconteceu antes. ...

. , . , . , . , . , , . . , .



t . , t = 0 — , t + 1 — . () . , . — .



t, — t + 1.

Uma rede neural recorrente pode ser visualizada como mostrado na Fig. 8.3: Os círculos correspondem a camadas inteiras de uma rede neural feedforward, consistindo de um ou mais neurônios. A saída da camada oculta é fornecida pela rede como de costume, mas depois retorna como sua própria entrada (camada oculta) junto com os dados de entrada usuais da próxima etapa de tempo. O diagrama descreve esse loop de feedback como um arco que vai da saída da camada de volta à entrada.



Uma maneira mais fácil (e mais comumente usada) de ilustrar esse processo é usar a implantação de rede. A Figura 8.4 mostra uma rede de cabeça para baixo com duas varreduras da variável de tempo (t) - camadas para as etapas t + 1 e t + 2.





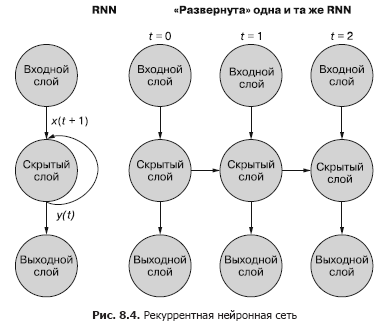
Cada uma das etapas de tempo corresponde a uma versão expandida da mesma rede neural na forma de uma coluna de neurônios. É como assistir a um script ou quadros de vídeo individuais de uma rede neural a qualquer momento. A rede à direita representa uma versão futura da rede à esquerda. O sinal de saída da camada oculta no tempo (t) é realimentado para a entrada da camada oculta junto com os dados de entrada para o próximo passo de tempo (t + 1) à direita. De novo. O diagrama mostra duas iterações dessa implantação, um total de três colunas de neurônios para t = 0, t = 1 e t = 2.



Todas as rotas verticais neste diagrama são completamente análogas, eles mostram os mesmos neurônios. Eles refletem a mesma rede neural em diferentes pontos no tempo. Essa representação visual é útil para demonstrar o movimento para frente e para trás de informações na rede durante a propagação de um erro. Mas lembre-se ao olhar para essas três redes implantadas: são instantâneos diferentes da mesma rede com o mesmo conjunto de pesos.



Vamos dar uma olhada na representação original da rede neural recorrente antes de implantá-la e mostrar a relação dos sinais de entrada e pesos. As camadas individuais deste RNN têm a aparência mostrada na Fig. 8,5 e 8,6.





Todos os neurônios em estado latente têm um conjunto de pesos aplicados a cada um dos elementos de cada um dos vetores de entrada, como em uma rede feedforward convencional. Mas, neste esquema, apareceu um conjunto adicional de pesos treináveis, que são aplicados aos sinais de saída de neurônios ocultos da etapa de tempo anterior. A rede, por treinamento, seleciona os pesos apropriados (importância) dos eventos anteriores ao inserir a sequência token por token.

«», t = 0 t – 1. «» , , . t = 0 . , .

De volta aos dados, imagine que você tem um conjunto de documentos, cada um dos quais é um exemplo rotulado. E, em vez de passar todo o conjunto de vetores de palavras para a rede neural convolucional para cada amostra, como no capítulo anterior (Figura 8.7), transferimos os dados de amostra para o RNN, um token por vez (Figura 8.8).





Passamos um vetor de palavras para o primeiro token e obtemos a saída de nossa rede neural recorrente. Em seguida, transferimos o segundo token e com ele o sinal de saída do primeiro! Depois disso, transferimos o terceiro token junto com o sinal de saída do segundo! Etc. Agora, em nossa rede neural, existem conceitos de "antes" e "depois", causa e efeito, alguma, embora vaga, noção de tempo (ver Fig. 8.8).





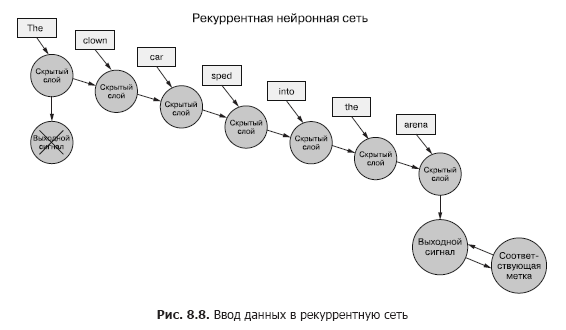
Agora nossa rede já está lembrando de algo! Bem, até certo ponto. Ainda há algumas coisas a serem descobertas. Em primeiro lugar, como pode ocorrer a propagação reversa de um erro em tal estrutura?

8.1.1. Propagação reversa de um erro no tempo

Todas as redes discutidas acima tiveram o rótulo de destino (variável de destino) e RNN não é exceção. Mas não temos o conceito de um rótulo para cada token e há apenas um rótulo para todos os tokens de cada texto de amostra. Temos apenas etiquetas para documentos de amostra.

Estamos falando de tokens como entrada para a rede em cada etapa de tempo, mas as redes neurais recorrentes também podem funcionar com quaisquer dados de série temporal. Os tokens podem ser qualquer um, discreto ou contínuo: leituras de estações meteorológicas, notas, símbolos em uma frase, etc.

Aqui, primeiro comparamos a saída da rede na última etapa de tempo com a sugestão. Isso é o que iremos (por agora) chamar de erro, ou seja, nossa rede está tentando minimizá-lo. Mas há uma ligeira diferença em relação aos capítulos anteriores. Uma determinada amostra de dados é dividida em pedaços menores que são alimentados na rede neural sequencialmente. No entanto, em vez de usar diretamente a saída para cada um desses subexemplos, nós a enviamos de volta para a rede.



Até agora, estamos interessados ​​apenas no sinal de saída final. Cada um dos tokens na sequência é alimentado na rede e as perdas são calculadas com base na saída da última etapa de tempo (token) (Figura 8.9).





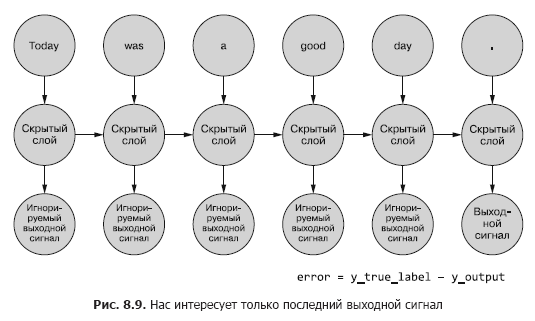
É necessário determinar, se há um erro para um determinado exemplo, quais pesos atualizar e quanto. No Capítulo 5, mostramos como retropropagar um erro em uma rede normal. E sabemos que a quantidade de correção de peso depende de sua (esse peso) contribuição para o erro. Podemos alimentar um token de uma sequência de amostra para a entrada da rede, calculando o erro para a etapa de tempo anterior com base em seu sinal de saída. É aqui que a ideia de retropropagar um erro no tempo parece confundir tudo.



No entanto, pode-se simplesmente pensar nisso como um processo com limite de tempo. Em cada etapa de tempo, os tokens, começando do primeiro em t = 0, são alimentados um de cada vez para a entrada do neurônio oculto localizado na frente - a próxima coluna na Fig. 8,9. Ao mesmo tempo, a rede se expande, revelando a próxima coluna da rede, já pronta para receber o próximo token na sequência. Os neurônios latentes se desdobram um de cada vez, como uma caixa de música ou um piano mecânico. No final, quando todos os elementos dos exemplos forem alimentados na rede, não haverá mais nada para implantar e obteremos o rótulo final para a variável alvo de nosso interesse, que pode ser usada para calcular o erro e ajustar os pesos. Acabamos de percorrer todo o caminho para baixo no gráfico de computação para esta rede desenrolada.



Por enquanto, consideramos as entradas geralmente estáticas. Você pode rastrear em todo o gráfico qual sinal de entrada vai para qual neurônio. E como sabemos como cada neurônio funciona, podemos propagar o erro de volta ao longo da cadeia, ao longo do mesmo caminho, assim como no caso de uma rede neural feedforward convencional.



Para propagar o erro de volta à camada anterior, usaremos a regra da cadeia. Em vez da camada anterior, propagaremos o erro para a mesma camada do passado, como se todas as variantes de rede implantadas fossem diferentes (Figura 8.10). Isso não muda a matemática do cálculo.





O erro se propaga desde a última etapa. O gradiente de uma etapa de tempo anterior em relação a uma mais recente é calculado. Depois de calcular todos os gradientes baseados em tokens individuais até a etapa t = 0 para este exemplo, as alterações são agregadas e aplicadas a um conjunto de pesos.

8.1.2. Quando atualizar o que

Transformamos nosso estranho RNN em algo como uma rede neural feedforward normal, então atualizar os pesos não deve ser muito difícil. No entanto, há uma ressalva. O truque é que os pesos não são atualizados em nenhum outro ramo da rede neural. Cada filial representa a mesma rede em diferentes pontos no tempo. Os pesos para cada etapa de tempo são os mesmos (consulte a Figura 8.10).



Uma solução simples para este problema é calcular as correções para os pesos em cada uma das etapas de tempo com um atraso na atualização. Em uma rede feedforward, todas as atualizações dos pesos são calculadas imediatamente após o cálculo de todos os gradientes para um determinado sinal de entrada. E aqui é exatamente o mesmo, mas as atualizações são adiadas até que cheguemos ao intervalo de tempo inicial (zero) para dados de amostra de entrada específicos.



O cálculo do gradiente deve ser baseado nos valores dos pesos com os quais eles contribuíram para o erro. Aqui está a parte mais opressora: o peso na etapa de tempo t contribuiu de alguma forma para o erro. E o mesmo peso recebe um sinal de entrada diferente na etapa de tempo t + 1, o que significa que faz uma contribuição diferente para o erro.



Você pode calcular as várias alterações nos pesos em cada etapa de tempo, somá-los e, em seguida, aplicar as alterações agrupadas aos pesos da camada oculta como a última etapa da fase de treinamento.

, . , , . , , . , .

Mágica real. Quando o erro se propaga de volta no tempo, o peso individual pode ser corrigido em uma direção em uma etapa de tempo t (dependendo de sua resposta ao sinal de entrada em uma etapa de tempo t), e então na outra direção em uma etapa de tempo t - 1 (de acordo com como ele reagiu ao sinal de entrada na etapa de tempo t - 1) para um dado de amostra! Lembre-se de que as redes neurais em geral se baseiam na minimização da função de perda, independentemente da complexidade das etapas intermediárias. Coletivamente, a rede otimiza esse recurso complexo. Como a atualização de peso é aplicada apenas uma vez para os dados de exemplo, a rede (se houver convergência, é claro) eventualmente para no peso ideal nesse sentido para um sinal de entrada específico e um neurônio específico.

Os resultados das etapas anteriores ainda são importantes

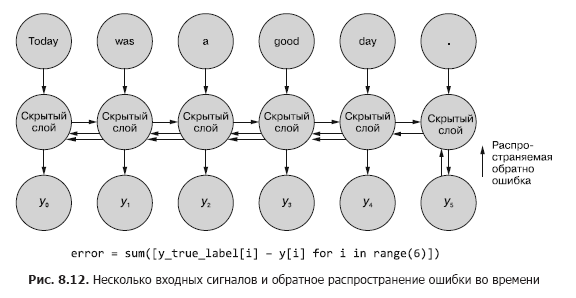
Às vezes, toda a sequência de valores gerados em todas as etapas intermediárias de tempo é importante. No Capítulo 9, forneceremos exemplos de situações em que a saída de uma determinada etapa de tempo t é tão importante quanto a saída da última etapa de tempo. Na fig. 8.11 mostra um método para coletar dados de erro para qualquer intervalo de tempo e propagá-los de volta para corrigir todos os pesos da rede.





Este processo se assemelha à retropropagação usual de um erro no tempo para n etapas de tempo. Nesse caso, propagamos o bug de várias fontes ao mesmo tempo. Mas, como no primeiro exemplo, os ajustes de peso são aditivos. O erro se propaga da última etapa de tempo no início para a primeira com a soma das mudanças em cada um dos pesos. Então a mesma coisa acontece com o erro calculado no penúltimo intervalo de tempo, somando todas as mudanças até t = 0. Esse processo é repetido até atingirmos o passo de tempo zero com propagação de volta do erro para ele como se fosse o único. Em seguida, as alterações cumulativas são aplicadas todas de uma vez à camada oculta correspondente.



Na fig. A Figura 8.12 mostra como o erro se propaga de cada sinal de saída de volta até t = 0 e, em seguida, é agregado antes da correção final dos pesos. Esta é a ideia principal desta seção. Como no caso de uma rede neural feedforward convencional, os pesos são atualizados apenas após o cálculo da mudança proposta nos pesos para toda a etapa de retropropagação para um determinado sinal de entrada (ou conjunto de sinais de entrada). No caso de RNN, a propagação reversa do erro inclui atualizações até o tempo t = 0.



Atualizar os pesos anteriormente teria distorcido os cálculos de gradiente com erros de propagação reversa em momentos anteriores. Lembre-se de que os gradientes são calculados em relação a um peso específico. Se este peso for atualizado muito cedo, digamos na etapa de tempo t, então, ao calcular o gradiente na etapa de tempo t-1, o valor do peso (lembre-se de que esta é a mesma posição do peso na rede) mudará. E ao calcular o gradiente com base no sinal de entrada do intervalo de tempo t-1, os cálculos serão distorcidos. Na verdade, neste caso, o peso será multado (ou recompensado) pelo que for “não tem culpa”!

Sobre os autores

Hobson Lane(Hobson Lane) tem 20 anos de experiência na construção de sistemas autônomos que tomam decisões críticas para o benefício das pessoas. Na Talentpair, Hobson ensinou as máquinas a ler e compreender currículos de maneira menos tendenciosa do que a maioria dos gerentes de contratação. Em Aira, ele ajudou a construir seu primeiro chatbot projetado para interpretar o mundo para cegos. Hobson é um admirador apaixonado da abertura da IA ​​e da orientação voltada para a comunidade. Ele faz contribuições ativas para projetos de código aberto, como Keras, scikit-learn, PyBrain, PUGNLP e ChatterBot. Ele está atualmente envolvido em pesquisas abertas e projetos educacionais para a Total Good, incluindo a criação de um assistente virtual de código aberto. Ele publicou vários artigos, lecionou na AIAA, PyCon,PAIS e IEEE e recebeu várias patentes na área de robótica e automação.



Hannes Max Hapke é um engenheiro elétrico que se tornou engenheiro de aprendizado de máquina. No colégio, ele se interessou por redes neurais quando estudou como computar redes neurais em microcontroladores. Mais tarde na faculdade, ele aplicou os princípios das redes neurais ao gerenciamento eficiente de usinas de energia renovável. Hannes é apaixonado por automatizar o desenvolvimento de software e pipelines de aprendizado de máquina. Ele é coautor de modelos de aprendizado profundo e canais de aprendizado de máquina para os setores de recrutamento, energia e saúde. Hannes fez apresentações sobre aprendizado de máquina em uma variedade de conferências, incluindo OSCON, Open Source Bridge e Hack University.



Cole Howard(Cole Howard) é um praticante de aprendizado de máquina, praticante de PNL e escritor. Um eterno buscador de padrões, ele se viu no mundo das redes neurais artificiais. Entre seus desenvolvimentos estão sistemas de recomendação em larga escala para negociação pela Internet e redes neurais avançadas para sistemas de inteligência de máquina ultradimensionais (redes neurais profundas), que ocupam os primeiros lugares nas competições Kaggle. Ele deu palestras sobre redes neurais convolucionais, redes neurais recorrentes e seu papel no processamento de linguagem natural nas conferências Open Source Bridge e Hack University.





»Mais detalhes sobre o livro podem ser encontrados no site da editora

» Índice

» Trecho



Para Habitantes desconto de 25% no cupom - PNL No



ato do pagamento da versão em papel do livro, é enviado um e-book para o e-mail.