O que é música em termos de matemática? O que é "la" ou "mi"? Como exatamente os sons são formados é bem conhecido no violão.
Som "mi" (som livre da 1ª corda), som “la” ( 1ª corda presa na 5ª casa ). "La" é 440 Hz. O que significa 440 Hz? Isso é 440 vezes a corda vibra por segundo. O som "mi" é 5 semitons mais baixo que o som "la" ( preso no 5º traste ).

Mais 7 semitons abaixo, obterei "mi" novamente, ou seja, oitava. Por que tanto o som livre da primeira corda quanto o som da corda presa na 12ª casa são chamados de "mi"?

Parece-nos que a mesma nota está sendo tocada. O fato é que o comprimento da corda neste ponto ( "mi" no 12º traste ) é dividido exatamente pela metade:
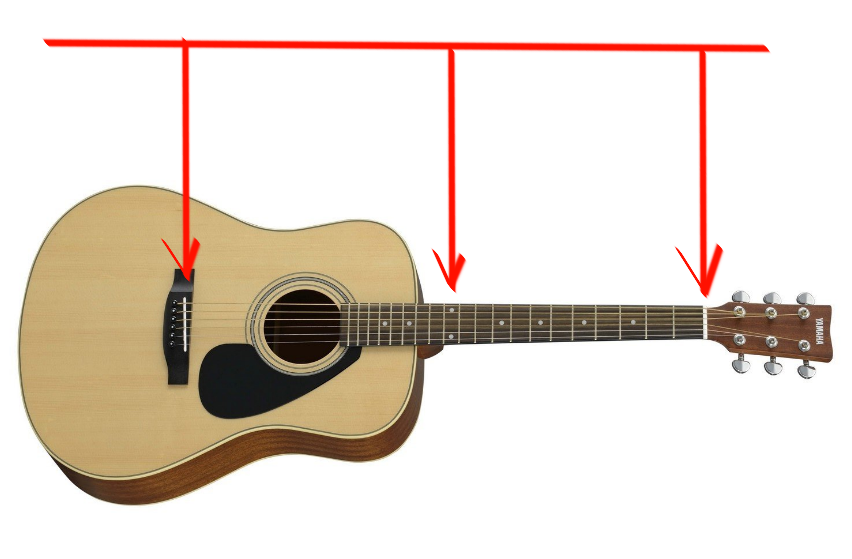
isso significa que as vibrações desse resto da corda, de acordo com as leis da física, serão duas vezes mais frequentes que as vibrações de uma corda inteira.
Cada vez que desço a corda e a prendo na próxima casa ( divisão indicada pela linha perpendicular do braço ), o som sobe um semitom, como dizem os músicos.
Observe que os trastes na escala são de larguras diferentes. Eles diminuem gradualmente, porque para aumentar a frequência em um semitom, é necessário reduzir o comprimento da corda em um determinado número de vezes.
O que estou sugerindo ao me concentrar no fato de que algo "ligado" é traduzido em algo "dentro"? Os matemáticos diriam que há apenas uma (sob certas condições) função onde + vai para x ( multiplicação ). E essa função é chamada de logaritmo.
Isso significa que nossos ouvidos, encurtando as cordas e aumentando o som um certo número de vezes, percebem que ele está aumentando um semitom. Ou seja, cada traste encurta a corda no mesmo número de vezes, e nossos ouvidos dizem que subimos um semitom, atingindo a nota "E" e recebendo uma oitava. Nossos órgãos auditivos são logarítmicos.
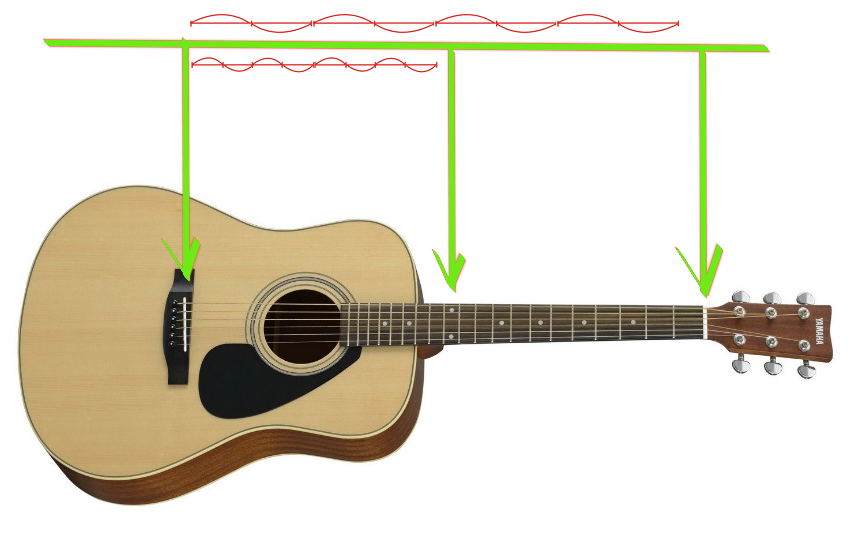
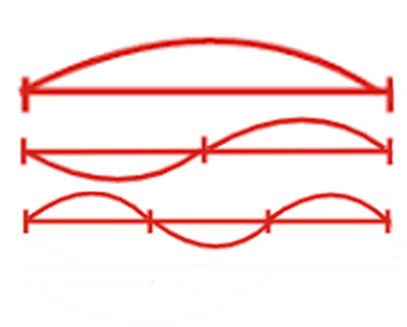
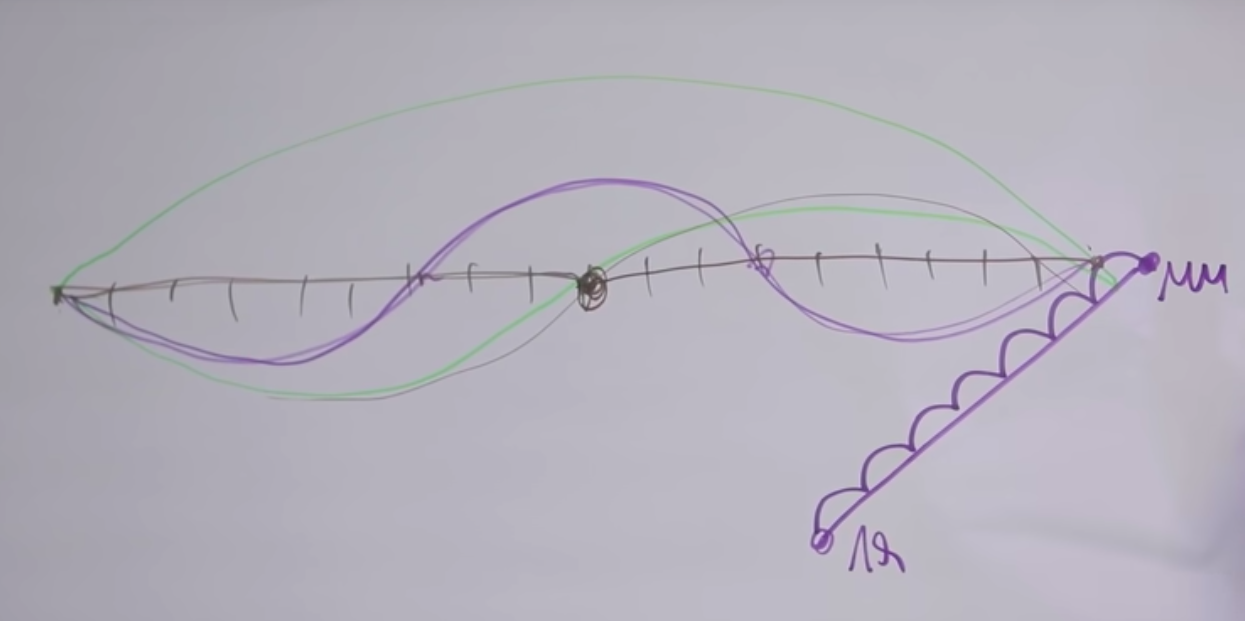
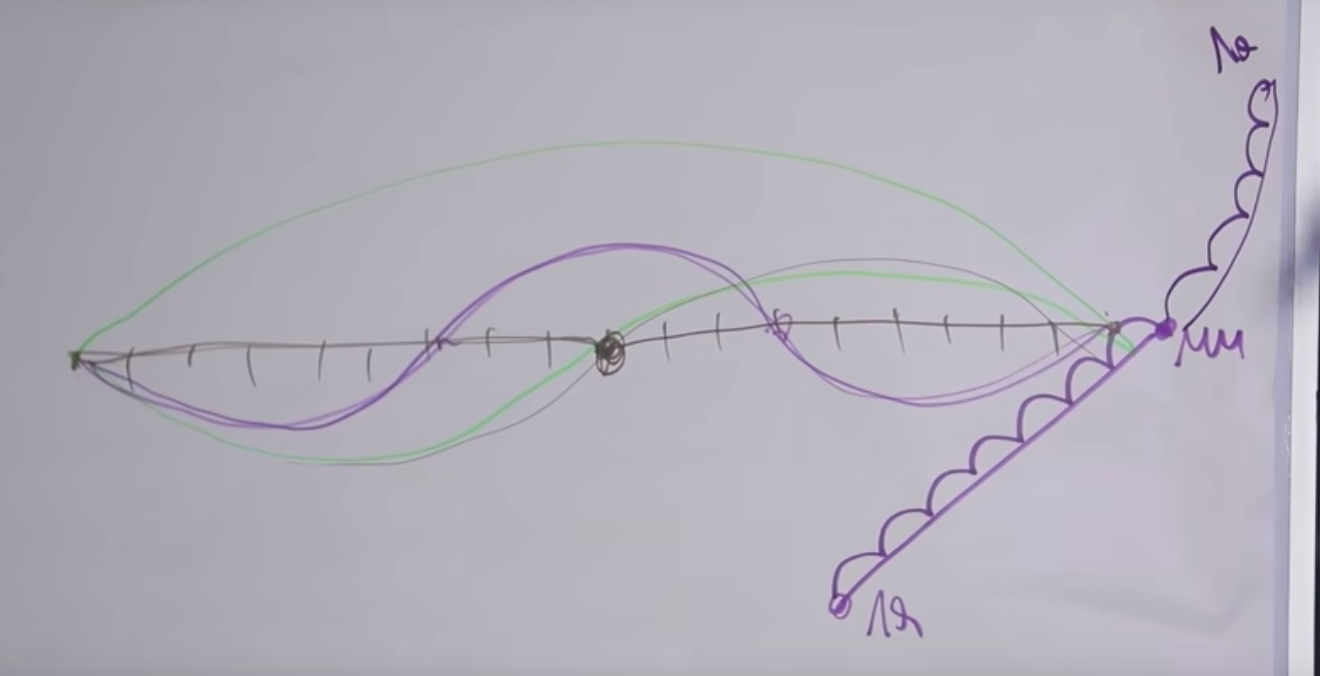
Dizemos que "mi" e "mi" são duas vezes diferentes, isso é evidente pelo som. O arco superior está em pleno andamento. Quando o prendemos no meio, a corda começa a vibrar, como no gráfico do meio.
Por que os sons são semelhantes? O fato é que junto com a vibração principal da corda, de fato, a vibração da mesma corda ocorre em todas as frequências, onde o comprimento da seção vibracional é inversamente proporcional à frequência.
Conseqüentemente, se o comprimento diminuir em um número inteiro de vezes, o sobretom correspondente pode ser ouvido. O sobretom correspondente é realizado pela string dada. Se uma determinada corda vibra parcialmente fixada nesses dois pontos ( gráfico inferior ), então seu tom será três vezes mais alto.
Um aumento duplo na frequência é percebido pelo ouvido como a mesma nota. Todos os sobretons que dividimos várias vezes, ou seja, qualquer divisão de meio segmento é uma divisão automática e um grande segmento. E apenas algumas divisões de um grande segmento não se enquadram no esquema de meia divisão.
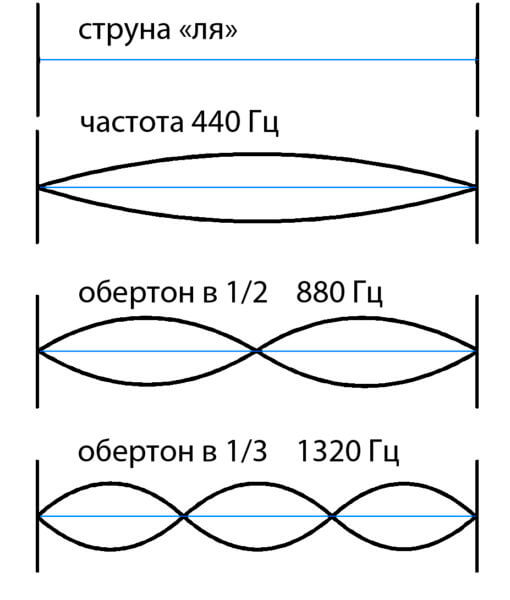
Se considerarmos os tons superiores pares para uma corda longa, eles serão os tons superiores para uma corda meio encurtada. E absolutamente qualquer som encurtado de uma corda curta soará para uma longa. Portanto, sentimos que tudo o que ouvimos coincide nesses pontos, e percebemos isso como uma nota.
É ainda mais interessante que existam notas que passam por vários semitons, e são percebidas pelos nossos ouvidos como uma consonância, um acorde, algo agradável ao ouvido, não corta nossos ouvidos. Quais são essas notas?
Se você pegar 7 semitons, pegue a nota "A" e aumente o som em 7 semitons, até o próximo "E", então essas duas notas soarão bem.
Se você recuar mais 5 semitons para cima, haverá um "la" mais alto na próxima oitava. Por alguma razão, esse intervalo também nos parece agradável. Vamos descobrir tudo.
Em primeiro lugar, se um aumento de 1 semitom é um aumento na frequência das oscilações por um certo número de vezes, então o designaremos como x. Se você precisar aumentar mais um semitom, já haverá x * x, ou seja, x 2 . Se eu aumentar em 12 semitons (x 12 ), ele deve aumentar exatamente 2 vezes. Obtemos a equação x 12 = 2.
Portanto, um aumento de 1 semitom significa uma contração da corda em x = 12√2, ou, o que é o mesmo, aumentando a frequência do som em 12 √2.
E o que "la" e "mi" têm a ver com isso? Por que 7 semitons soam melódicos? Vamos aumentar o grau:
O que é tão agradável, bom neste número?
Em algum momento da antiguidade, foram inventados craveiros temperados, uma gravação precisa de música. Você pode ver muito bem no violão, você também encontra no piano, está escondido por dentro, se você olhar dá para ver as cordas.
Agora, esse número está muito próximo de 3/2. Se você calcular em uma calculadora, será muito preciso. Isso significa que "mi" é aproximadamente 1,5 vezes maior que o "la" anterior. Essa. levantar 7 tons é equivalente a subir 3/2 vezes, o que significa que temos muitos sobretons superiores coincidentes.
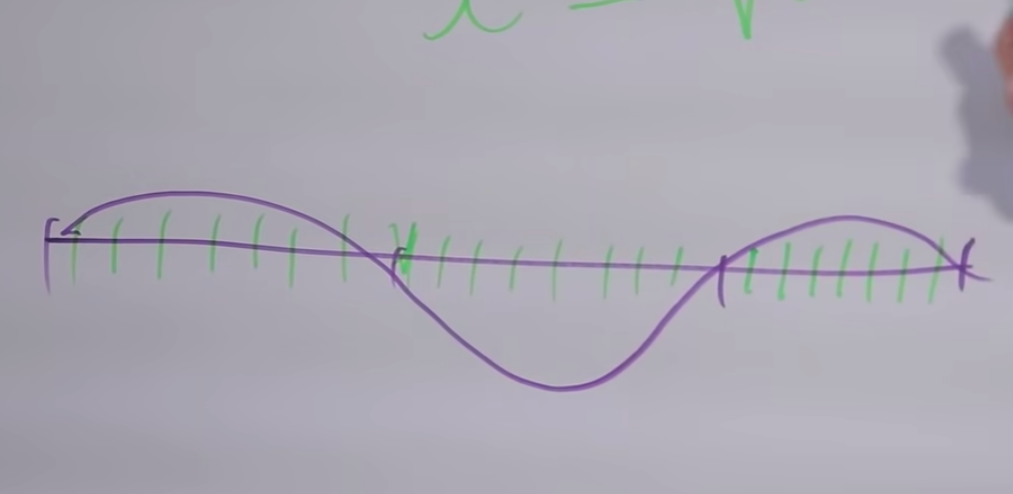
Porque qualquer divisão por um inteiro de um pequeno segmento será uma divisão inteira de todo o segmento. E, portanto, dividir o corte original pelo número de peças, um múltiplo de três, será a divisão do segmento pequeno (⅓), e ⅔ também. Quando saímos ⅔ do comprimento, ou seja, aumentamos a frequência para 3/2, subimos cerca de 7 semitons, teremos muitos sobretons comuns, será uma consonância agradável.
Os 4/3 restantes são exatamente os 5 semitons restantes, 3/2 x 4/3 = 2, apenas uma oitava. Que corresponde à fórmula x71243. O valor está muito próximo de 4/3, mas não 100%. Este número é irracional, não pode ser escrito como uma fração, não pode ser escrito como um inteiro dividido por um inteiro.
Ouvi dizer que existe um instrumento na Índia ( cítara), em que a oitava é dividida em 19 partes, ou seja, eles têm um semitom = 1/19 oitava, 19x2.

E já com grande precisão x121932, o que significa que se em tal instrumento indiano você recuar 12 dos 19 segmentos, então nesta consonância haverá mais sobretons coincidentes, e este intervalo soa como um bálsamo para os ouvidos.
Há muitas coisas interessantes a dizer sobre música e matemática. Em particular, um acorde maior é percebido se 4 semitons são adicionados a qualquer nota inicial e, em seguida, 3, ou seja, 0 - 4 - 3. Um menor, se você adicionar 3 no início e, em seguida, 4, ou seja, 0 - 3 - 4. A primeira e a última das três notas do acorde serão "iguais", apenas diferem em 7 semitons, mas o som do meio criará nossa percepção de consonância e afinará em modo maior ou menor.
Parece que música e matemática, o que pode haver em comum? E há tanto em comum que matemáticos e músicos costumam se comunicar, além disso, os matemáticos entendem facilmente os músicos, por assim dizer, eles alcançam um semitom.
Vários links úteis: