
Olá a todos, hoje trataremos do algoritmo de compressão JPEG. Muitas pessoas não sabem que JPEG não é tanto um formato quanto um algoritmo. A maioria das imagens JPEG que você vê está em JFIF (JPEG File Interchange Format), dentro do qual o algoritmo de compactação JPEG é aplicado. Ao final do artigo, você terá um entendimento muito melhor de como esse algoritmo compacta dados e como escrever código de descompactação em Python. Não consideraremos todas as nuances do formato JPEG (por exemplo, varredura progressiva), mas apenas falaremos sobre os recursos básicos do formato enquanto estamos escrevendo nosso próprio decodificador.
Introdução
Por que escrever outro artigo sobre JPEG quando centenas de artigos já foram escritos sobre ele? Normalmente, nesses artigos, os autores falam apenas sobre qual é o formato. Você não escreve código de descompactação e decodificação. E se você escrever algo, será em C / C ++, e este código não estará disponível para uma grande variedade de pessoas. Quero quebrar essa tradição e mostrar a você, com Python 3, como funciona um decodificador JPEG básico. Ele será baseado neste código desenvolvido pelo MIT, mas vou alterá-lo bastante por uma questão de legibilidade e clareza. Você pode encontrar o código modificado para este artigo em meu repositório .
Partes diferentes de JPEG
Vamos começar com uma foto feita por Ange Albertini . Ele lista todas as partes de um arquivo JPEG simples. Analisaremos cada segmento e, ao ler o artigo, você retornará a esta ilustração mais de uma vez.
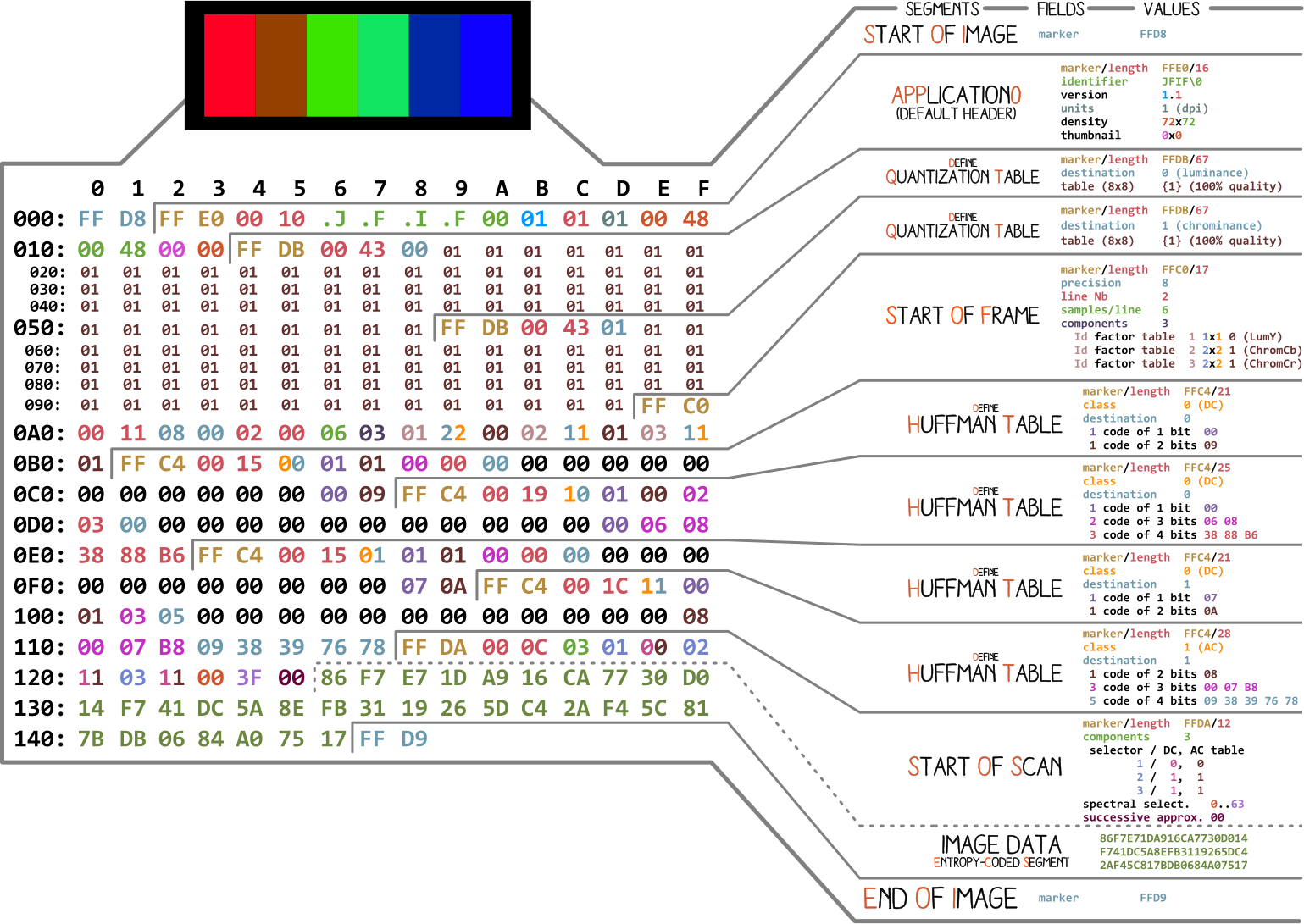
Quase todo arquivo binário contém vários marcadores (ou cabeçalhos). Você pode pensar neles como algum tipo de marcador. Eles são essenciais para trabalhar com o arquivo e são usados por programas como o arquivo (no Mac e Linux) para que possamos saber os detalhes do arquivo. Os marcadores indicam exatamente onde certas informações são armazenadas no arquivo. Na maioria das vezes, os marcadores são colocados de acordo com o valor do comprimento (
length) de um segmento específico.
Início e fim do arquivo
O primeiro marcador importante para nós é
FF D8. Ele define o início da imagem. Se não o encontrarmos, podemos assumir que o marcador está em algum outro arquivo. O marcador não é menos importante FF D9. Diz que chegamos ao fim do arquivo de imagem. Após cada marcador, exceto para o intervalo FFD0- FFD9e FF01, imediatamente vem o valor do comprimento do segmento deste marcador. E os marcadores de início e fim do arquivo sempre têm dois bytes de comprimento.
Estaremos trabalhando com esta imagem:

Vamos escrever um código para encontrar os marcadores de início e fim.
from struct import unpack
marker_mapping = {
0xffd8: "Start of Image",
0xffe0: "Application Default Header",
0xffdb: "Quantization Table",
0xffc0: "Start of Frame",
0xffc4: "Define Huffman Table",
0xffda: "Start of Scan",
0xffd9: "End of Image"
}
class JPEG:
def __init__(self, image_file):
with open(image_file, 'rb') as f:
self.img_data = f.read()
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
elif marker == 0xffda:
data = data[-2:]
else:
lenchunk, = unpack(">H", data[2:4])
data = data[2+lenchunk:]
if len(data)==0:
break
if __name__ == "__main__":
img = JPEG('profile.jpg')
img.decode()
# OUTPUT:
# Start of Image
# Application Default Header
# Quantization Table
# Quantization Table
# Start of Frame
# Huffman Table
# Huffman Table
# Huffman Table
# Huffman Table
# Start of Scan
# End of Image
Para descompactar os bytes da imagem, usamos struct .
>Hdiz a structele para ler o tipo de dados unsigned shorte trabalhar com eles em ordem de alto para baixo (big-endian). Os dados JPEG são armazenados do maior para o menor formato. Apenas os dados EXIF podem estar no formato little-endian (embora normalmente não seja o caso). E o tamanho shorté 2, então transferimos unpackdois bytes de img_data. Como sabemos o que é short? Sabemos que os marcadores estão em JPEG são indicados por quatro caracteres hexadecimais: ffd8. Um desses caracteres é equivalente a quatro bits (meio byte), então quatro caracteres serão equivalentes a dois bytes, assim como short.
Após a seção Início da digitalização, os dados da imagem digitalizada seguem imediatamente, os quais não têm um comprimento específico. Eles continuam até o final do marcador de arquivo, portanto, enquanto “procuramos” manualmente por ele, encontramos o marcador de início de digitalização.
Agora, vamos lidar com o resto dos dados da imagem. Para fazer isso, primeiro estudamos a teoria e depois passamos para a programação.
Codificação JPEG
Primeiro, vamos falar sobre os conceitos básicos e as técnicas de codificação usadas no JPEG. E a codificação será feita na ordem inversa. Na minha experiência, a decodificação será difícil de descobrir sem ele.
A ilustração abaixo ainda não está clara para você, mas darei dicas conforme você aprende o processo de codificação e decodificação. Estas são as etapas para codificação JPEG ( fonte ):
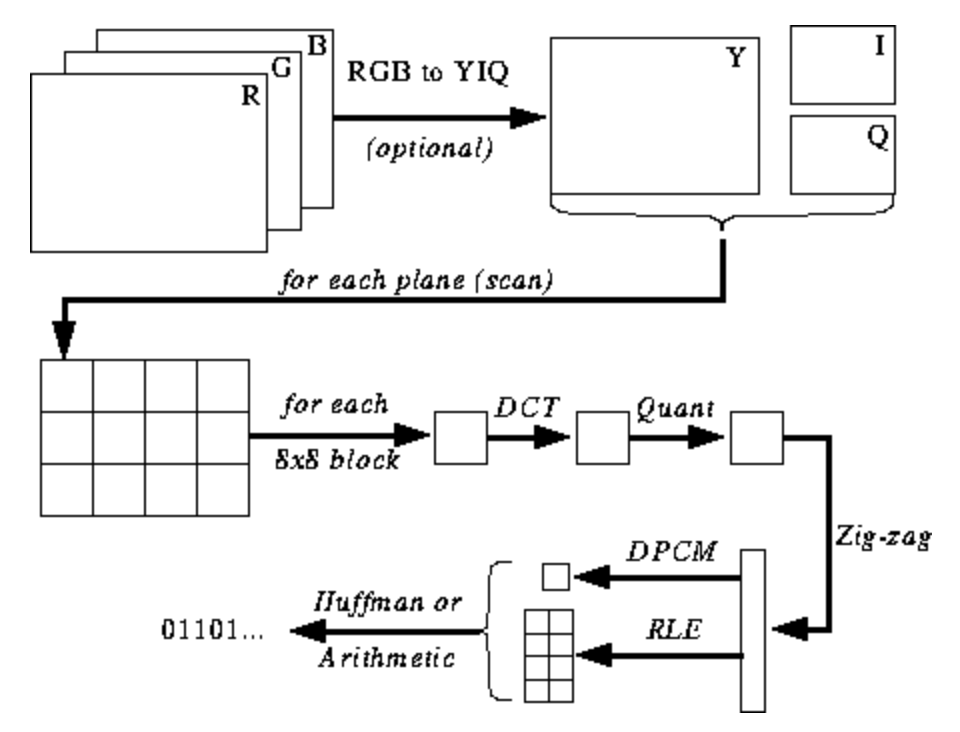
Espaço de cor JPEG
De acordo com a especificação JPEG ( ISO / IEC 10918-6: 2013 (E) Seção 6.1):
- Imagens codificadas com apenas um componente são tratadas como dados em tons de cinza, onde 0 é preto e 255 é branco.
- Imagens codificadas com três componentes são consideradas dados RGB codificados no espaço YCbCr. Se a imagem contém o segmento do marcador APP14 descrito na Seção 6.5.3, a codificação de cores é considerada RGB ou YCbCr de acordo com as informações no segmento do marcador APP14. A relação entre RGB e YCbCr é definida de acordo com ITU-T T.871 | ISO / IEC 10918-5.
- , , CMYK-, (0,0,0,0) . APP14, 6.5.3, CMYK YCCK APP14. CMYK YCCK 7.
A maioria das implementações do algoritmo JPEG usa luminância e crominância (codificação YUV) em vez de RGB. Isso é muito útil porque o olho humano é muito pobre em distinguir mudanças de alta frequência no brilho em áreas pequenas, então você pode reduzir a frequência e a pessoa não notará a diferença. O que isso faz? Imagem altamente compactada com degradação de qualidade quase imperceptível.
Como no RGB, cada pixel é codificado com três bytes de cores (vermelho, verde e azul), portanto, no YUV, três bytes são usados, mas seu significado é diferente. O componente Y define o brilho da cor (luminância ou luma). U e V definem a cor (croma): U é responsável pela porção azul e V pela porção vermelha.
Esse formato foi desenvolvido em uma época em que a televisão ainda não era tão comum e os engenheiros queriam usar o mesmo formato de codificação de imagem para transmissões de televisão em cores e em preto e branco. Leia mais sobre isso aqui .
Transformada discreta de cosseno e quantização
JPEG converte a imagem em blocos de 8x8 pixels (chamados de MCU, Minimum Coding Unit), altera o intervalo de valores de pixel para que o centro seja 0 e, em seguida, aplica uma transformação de cosseno discreta a cada bloco e compacta o resultado usando quantização. Vamos ver o que tudo isso significa.
Transformada discreta de cosseno (DCT) é um método de transformar dados discretos em combinações de ondas de cosseno. Converter uma imagem em um conjunto de cossenos parece um exercício fútil à primeira vista, mas você entenderá o motivo quando aprender sobre as próximas etapas. O DCT pega um bloco de 8x8 pixels e nos diz como reproduzir esse bloco usando uma matriz de funções cosseno de 8x8. Mais detalhes aqui .
A matriz é semelhante a esta:

Aplicamos DCT separadamente para cada componente de pixel. Como resultado, obtemos uma matriz de coeficientes 8x8, que mostra a contribuição de cada (de todas as 64) funções cosseno na matriz 8x8 de entrada. Na matriz de coeficientes DCT, os maiores valores são geralmente encontrados no canto superior esquerdo e os menores no canto inferior direito. A parte superior esquerda é a função cosseno de frequência mais baixa e a parte inferior direita é a mais alta.
Isso significa que, na maioria das imagens, há uma grande quantidade de informações de baixa frequência e uma pequena proporção de informações de alta frequência. Se os componentes inferiores à direita de cada matriz DCT forem atribuídos a um valor de 0, a imagem resultante terá a mesma aparência para nós, porque uma pessoa não distingue mal as alterações de alta frequência. Isso é o que faremos na próxima etapa.
Eu encontrei um ótimo vídeo sobre este assunto. Veja se você não entende o significado da PrEP:
Todos nós sabemos que JPEG é um algoritmo de compressão com perdas. Mas até agora não perdemos nada. Temos apenas blocos de componentes YUV 8x8 convertidos em blocos de funções cosseno 8x8 sem perda de informação. O estágio de perda de dados é a quantização.
Quantização é o processo em que pegamos dois valores de uma certa faixa e os transformamos em um valor discreto. Em nosso caso, esse é apenas um nome astuto para reduzir a 0 os coeficientes de frequência mais altos na matriz DCT resultante. Ao salvar uma imagem usando JPEG, a maioria dos editores de imagem pergunta que nível de compactação você deseja definir. É aqui que ocorre a perda de informações de alta frequência. Você não poderá mais recriar a imagem original da imagem JPEG resultante.
Diferentes matrizes de quantização são usadas dependendo da taxa de compressão (curiosidade: a maioria dos desenvolvedores tem patentes para criar uma tabela de quantização). Dividimos a matriz DCT de coeficientes elemento a elemento pela matriz de quantização, arredondamos os resultados para inteiros e obtemos a matriz quantizada.
Vejamos um exemplo. Digamos que haja uma matriz DCT:

E aqui está a matriz de quantização usual:
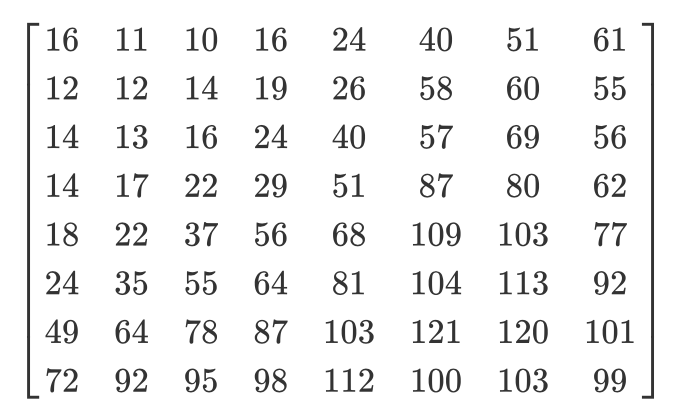
A matriz quantizada ficará assim:

Embora o ser humano não consiga ver as informações de alta frequência, se você remover muitos dados dos blocos de 8x8 pixels, a imagem ficará muito grosseira. Nessa matriz quantizada, o primeiro valor é chamado de valor DC e todos os outros são chamados de valores AC. Se pegássemos os valores DC de todas as matrizes quantizadas e gerássemos uma nova imagem, teríamos uma visualização com uma resolução 8 vezes menor que a imagem original.
Também quero observar que, como usamos a quantização, precisamos ter certeza de que as cores estão dentro da faixa de [0,255]. Se eles voarem para fora dela, você terá que trazê-los manualmente até essa distância.
Ziguezague
Após a quantização, o algoritmo JPEG usa uma varredura em zigue-zague para converter a matriz para a forma unidimensional:
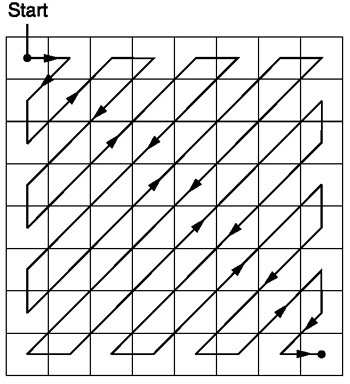
Fonte .
Vamos ter essa matriz quantizada:
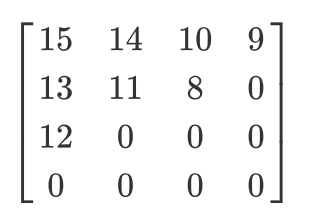
Então, o resultado da varredura em zigue-zague será o seguinte:
[15 14 13 12 11 10 9 8 0 ... 0]
Essa codificação é preferida porque após a quantização, a maioria das informações de baixa frequência (mais importantes) estará localizada no início da matriz, e a varredura em zigue-zague armazena esses dados no início da matriz unidimensional. Isso é útil para a próxima etapa, compactação.
Codificação de comprimento de execução e codificação delta
A codificação de execução é usada para compactar dados repetitivos. Após a varredura em ziguezague, vemos que há principalmente zeros no final da matriz. A codificação de comprimento nos permite aproveitar esse espaço desperdiçado e usar menos bytes para representar todos esses zeros. Digamos que temos os seguintes dados:
10 10 10 10 10 10 10
Depois de codificar os comprimentos da série, obtemos o seguinte:
7 10
Comprimimos 7 bytes em 2 bytes.
A codificação delta é usada para representar um byte em relação ao byte anterior. Será mais fácil explicar com um exemplo. Deixe-nos obter os seguintes dados:
10 11 12 13 10 9
Usando a codificação delta, eles podem ser representados da seguinte forma:
10 1 2 3 0 -1
Em JPEG, cada valor DC da matriz DCT é codificado em delta em relação ao valor DC anterior. Isso significa que, ao alterar o primeiro coeficiente DCT da imagem, você destruirá toda a imagem. Mas se você alterar o primeiro valor da última matriz DCT, isso afetará apenas um fragmento muito pequeno da imagem.
Essa abordagem é útil porque o primeiro valor DC da imagem geralmente varia mais, e usamos a codificação delta para trazer os valores DC restantes para mais perto de 0, o que melhora a compressão com a codificação Huffman.
Codificação Huffman
É um método de compressão sem perdas. Huffman uma vez se perguntou: "Qual é o menor número de bits que posso usar para armazenar texto livre?" Como resultado, um formato de codificação foi criado. Digamos que temos um texto:
a b c d e
Normalmente, cada caractere ocupa um byte de espaço:
a: 01100001
b: 01100010
c: 01100011
d: 01100100
e: 01100101
Este é o princípio da codificação ASCII binária. E se mudarmos o mapeamento?
# Mapping
000: 01100001
001: 01100010
010: 01100011
100: 01100100
011: 01100101
Agora precisamos de muito menos bits para armazenar o mesmo texto:
a: 000
b: 001
c: 010
d: 100
e: 011
Tudo bem, mas e se precisarmos economizar ainda mais espaço? Por exemplo, assim:
# Mapping
0: 01100001
1: 01100010
00: 01100011
01: 01100100
10: 01100101
a: 0
b: 1
c: 00
d: 01
e: 10
A codificação Huffman permite essa correspondência de comprimento variável. Os dados de entrada são obtidos, os caracteres mais comuns são combinados com uma combinação menor de bits e caracteres menos frequentes - com combinações maiores. E então os mapeamentos resultantes são coletados em uma árvore binária. No JPEG, armazenamos informações DCT usando a codificação Huffman. Lembra que mencionei que os valores DC de codificação delta tornam a codificação de Huffman mais fácil? Espero que agora você entenda o porquê. Após a codificação delta, precisamos combinar menos “caracteres” e o tamanho da árvore é reduzido.
Tom Scott tem um ótimo vídeo explicando como funciona o algoritmo de Huffman. Dê uma olhada antes de continuar lendo.
Um JPEG contém até quatro tabelas Huffman, que são armazenadas em "Definir Tabela Huffman" (começa com
0xffc4). Os coeficientes DCT são armazenados em duas tabelas de Huffman diferentes: em uma, valores DC das tabelas em zigue-zague, na outra - valores AC das tabelas em ziguezague. Isso significa que, ao codificar, precisamos combinar os valores DC e AC das duas matrizes. As informações DCT para os canais luma e cromaticidade são armazenadas separadamente, portanto, temos dois conjuntos de DC e dois conjuntos de informações AC, um total de 4 tabelas de Huffman.
Se a imagem estiver em tons de cinza, teremos apenas duas tabelas Huffman (uma para DC e outra para AC), porque não precisamos de cores. Como você deve ter percebido, duas imagens diferentes podem ter tabelas Huffman muito diferentes, por isso é importante armazená-las dentro de cada JPEG.
Agora sabemos o conteúdo principal das imagens JPEG. Vamos prosseguir para a decodificação.
Decodificação JPEG
A decodificação pode ser dividida em etapas:
- Extração de tabelas de Huffman e decodificação de bits.
- Extração de coeficientes DCT usando rollback de codificação de comprimento de execução e delta.
- Usando coeficientes DCT para combinar ondas de cosseno e reconstruir valores de pixel para cada bloco 8x8.
- Converta YCbCr em RGB para cada pixel.
- Exibe a imagem RGB resultante.
O padrão JPEG suporta quatro formatos de compressão:
- Base
- Série estendida
- Progressivo
- Sem perda
Vamos trabalhar com compressão básica. Ele contém uma série de blocos 8x8 seguidos uns dos outros. Em outros formatos, o modelo de dados é um pouco diferente. Para deixar claro, colori diferentes segmentos do conteúdo hexadecimal de nossa imagem:
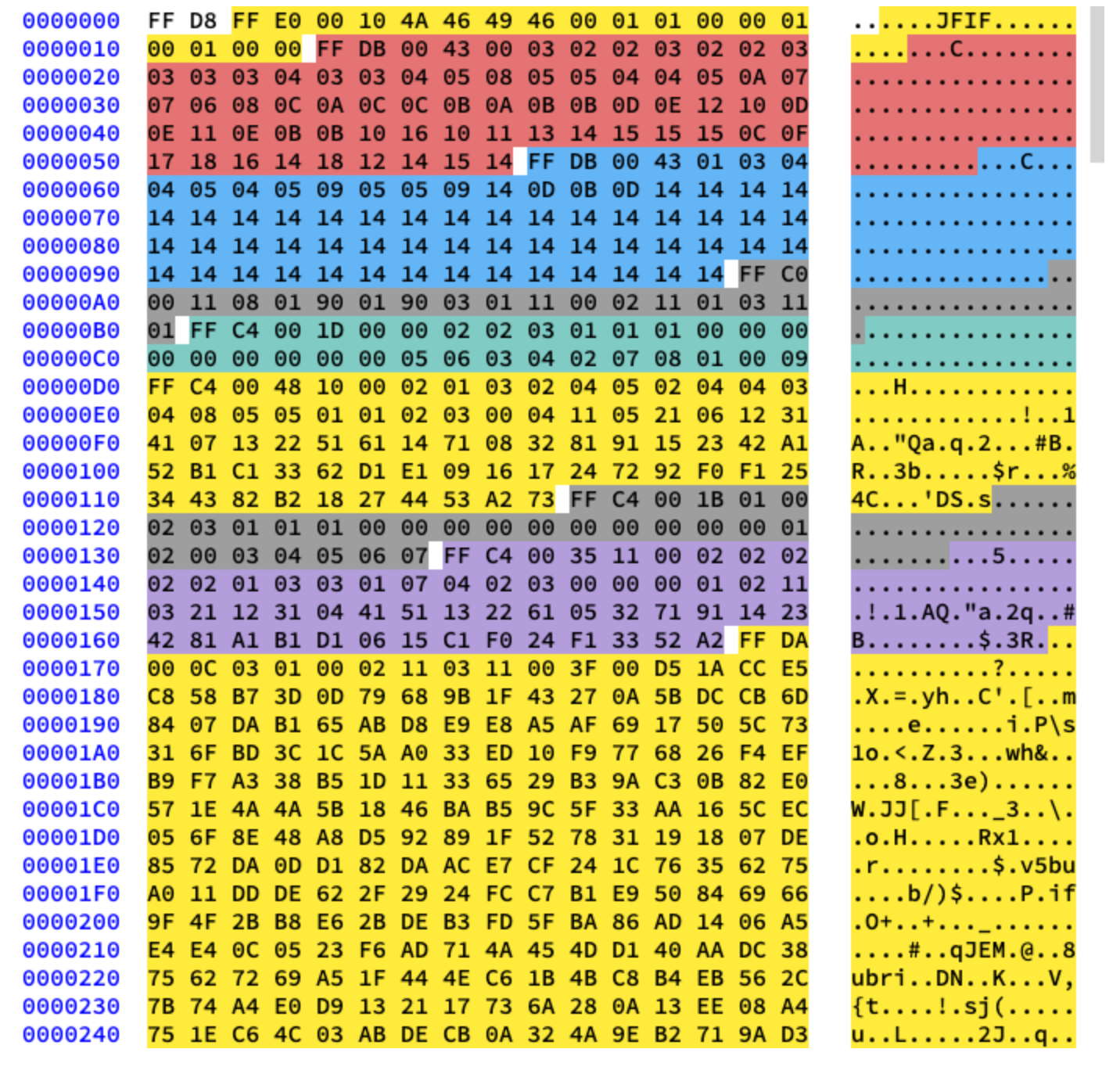
Extraindo tabelas de Huffman
Já sabemos que JPEG contém quatro tabelas de Huffman. Esta é a última codificação, então vamos começar a decodificar com ela. Cada seção com a tabela contém informações:
| Campo | O tamanho | Descrição |
|---|---|---|
| ID do marcador | 2 bytes | 0xff e 0xc4 identificam DHT |
| comprimento | 2 bytes | Comprimento da mesa |
| Informações da tabela Huffman | 1 byte | bits 0 ... 3: número de tabelas (0 ... 3, caso contrário, erro) bit 4: tipo de tabela, 0 = tabela DC, 1 = tabelas AC bits 5 ... 7: não usado, deve ser 0 |
| Personagens | 16 bytes | O número de caracteres com códigos de comprimento 1 ... 16, soma (n) desses bytes é o número total de códigos que devem ser <= 256 |
| Símbolos | n bytes | A tabela contém caracteres em ordem crescente de comprimento de código (n = número total de códigos). |
Digamos que temos uma tabela Huffman como esta ( fonte ):
| Símbolo | Código Huffman | Comprimento do código |
|---|---|---|
| uma | 00 | 2 |
| b | 010 | 3 |
| c | 011 | 3 |
| d | 100 | 3 |
| e | 101 | 3 |
| f | 110 | 3 |
| g | 1110 | 4 |
| h | 11110 | cinco |
| Eu | 111110 | 6 |
| j | 1111110 | 7 |
| k | 11111110 | 8 |
| eu | 111111110 | nove |
Ele será armazenado em um arquivo JFIF como este (em formato binário. Estou usando ASCII apenas para maior clareza):
0 1 5 1 1 1 1 1 1 0 0 0 0 0 0 0 a b c d e f g h i j k l
0 significa que não temos um código de Huffman de comprimento 1. Um 1 significa que temos um código de Huffman de comprimento 2 e assim por diante. Na seção DHT, imediatamente após a classe e o ID, os dados têm sempre 16 bytes de comprimento. Vamos escrever o código para extrair comprimentos e elementos do DHT.
class JPEG:
# ...
def decodeHuffman(self, data):
offset = 0
header, = unpack("B",data[offset:offset+1])
offset += 1
# Extract the 16 bytes containing length data
lengths = unpack("BBBBBBBBBBBBBBBB", data[offset:offset+16])
offset += 16
# Extract the elements after the initial 16 bytes
elements = []
for i in lengths:
elements += (unpack("B"*i, data[offset:offset+i]))
offset += i
print("Header: ",header)
print("lengths: ", lengths)
print("Elements: ", len(elements))
data = data[offset:]
def decode(self):
data = self.img_data
while(True):
# ---
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Depois de executar o código, obtemos o seguinte:
Start of Image
Application Default Header
Quantization Table
Quantization Table
Start of Frame
Huffman Table
Header: 0
lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 10
Huffman Table
Header: 16
lengths: (0, 2, 1, 3, 2, 4, 5, 2, 4, 4, 3, 4, 8, 5, 5, 1)
Elements: 53
Huffman Table
Header: 1
lengths: (0, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 8
Huffman Table
Header: 17
lengths: (0, 2, 2, 2, 2, 2, 1, 3, 3, 1, 7, 4, 2, 3, 0, 0)
Elements: 34
Start of Scan
End of Image
Excelente! Temos comprimentos e elementos. Agora você precisa criar sua própria classe de tabela Huffman para reconstruir a árvore binária a partir dos comprimentos e elementos obtidos. Vou apenas copiar o código daqui :
class HuffmanTable:
def __init__(self):
self.root=[]
self.elements = []
def BitsFromLengths(self, root, element, pos):
if isinstance(root,list):
if pos==0:
if len(root)<2:
root.append(element)
return True
return False
for i in [0,1]:
if len(root) == i:
root.append([])
if self.BitsFromLengths(root[i], element, pos-1) == True:
return True
return False
def GetHuffmanBits(self, lengths, elements):
self.elements = elements
ii = 0
for i in range(len(lengths)):
for j in range(lengths[i]):
self.BitsFromLengths(self.root, elements[ii], i)
ii+=1
def Find(self,st):
r = self.root
while isinstance(r, list):
r=r[st.GetBit()]
return r
def GetCode(self, st):
while(True):
res = self.Find(st)
if res == 0:
return 0
elif ( res != -1):
return res
class JPEG:
# -----
def decodeHuffman(self, data):
# ----
hf = HuffmanTable()
hf.GetHuffmanBits(lengths, elements)
data = data[offset:]
GetHuffmanBitspega os comprimentos e elementos, itera sobre os elementos e os coloca em uma lista root. É uma árvore binária e contém listas aninhadas. Você pode ler na Internet como a árvore de Huffman funciona e como criar essa estrutura de dados em Python. Para nosso primeiro DHT (da foto no início do artigo), temos os seguintes dados, comprimentos e elementos:
Hex Data: 00 02 02 03 01 01 01 00 00 00 00 00 00 00 00 00
Lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: [5, 6, 3, 4, 2, 7, 8, 1, 0, 9]
Após a chamada, a
GetHuffmanBitslista rootconterá os seguintes dados:
[[5, 6], [[3, 4], [[2, 7], [8, [1, [0, [9]]]]]]]
HuffmanTabletambém contém um método GetCodeque percorre a árvore e usa uma tabela de Huffman para retornar os bits decodificados. O método recebe um fluxo de bits como entrada - apenas uma representação binária dos dados. Por exemplo, o fluxo de bits para abcserá 011000010110001001100011. Primeiro, convertemos cada caractere em seu código ASCII, que convertemos em binário. Vamos criar uma classe para ajudar a converter uma string em bits e depois contar os bits um por um:
class Stream:
def __init__(self, data):
self.data= data
self.pos = 0
def GetBit(self):
b = self.data[self.pos >> 3]
s = 7-(self.pos & 0x7)
self.pos+=1
return (b >> s) & 1
def GetBitN(self, l):
val = 0
for i in range(l):
val = val*2 + self.GetBit()
return val
Ao inicializar, fornecemos dados binários à classe e, em seguida, os lemos usando
GetBite GetBitN.
Decodificando a tabela de quantização
A seção Definir Tabela de Quantização contém os seguintes dados:
| Campo | O tamanho | Descrição |
|---|---|---|
| ID do marcador | 2 bytes | 0xff e 0xdb identificam a seção DQT |
| comprimento | 2 bytes | Comprimento da tabela de quantização |
| Informação de quantização | 1 byte | bits 0 ... 3: número de tabelas de quantização (0 ... 3, caso contrário, erro) bits 4 ... 7: precisão da tabela de quantização, 0 = 8 bits, caso contrário, 16 bits |
| Bytes | n bytes | Valores da tabela de quantização, n = 64 * (precisão + 1) |
De acordo com o padrão JPEG, uma imagem JPEG padrão tem duas tabelas de quantização: para luma e croma. Eles começam com um marcador
0xffdb. O resultado do nosso código já contém dois desses marcadores. Vamos adicionar a capacidade de decodificar tabelas de quantização:
def GetArray(type,l, length):
s = ""
for i in range(length):
s =s+type
return list(unpack(s,l[:length]))
class JPEG:
# ------
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
with open(image_file, 'rb') as f:
self.img_data = f.read()
def DefineQuantizationTables(self, data):
hdr, = unpack("B",data[0:1])
self.quant[hdr] = GetArray("B", data[1:1+64],64)
data = data[65:]
def decodeHuffman(self, data):
# ------
for i in lengths:
elements += (GetArray("B", data[off:off+i], i))
offset += i
# ------
def decode(self):
# ------
while(True):
# ----
else:
# -----
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Primeiro definimos um método
GetArray. É apenas uma técnica conveniente para decodificar um número variável de bytes de dados binários. Também substituímos parte do código no método decodeHuffmanpara aproveitar as vantagens da nova função. Em seguida, o método foi definido DefineQuantizationTables: ele lê o título da seção com tabelas de quantização e, em seguida, aplica os dados de quantização ao dicionário usando o valor do cabeçalho como chave. este valor pode ser 0 para luminância e 1 para cromaticidade. Cada seção com tabelas de quantização em JFIF contém 64 bytes de dados (para uma matriz de quantização 8x8).
Se produzirmos as matrizes de quantização para nossa imagem, obtemos isso:
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
3 2 2 3 2 2 3 3
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
Decodificando o início do quadro
A seção Início do Quadro contém as seguintes informações ( fonte ):
| Campo | O tamanho | Descrição |
|---|---|---|
| ID do marcador | 2 bytes | 0xff 0xc0 SOF |
| 2 | 8 + *3 | |
| 1 | , 8 (12 16 ). | |
| 2 | > 0 | |
| 2 | > 0 | |
| 1 | 1 = , 3 = YcbCr YIQ | |
| 3 | 3 . (1 ) (1 = Y, 2 = Cb, 3 = Cr, 4 = I, 5 = Q), (1 ) ( 0...3 , 4...7 ), (1 ). |
Aqui não estamos interessados em tudo. Extrairemos a largura e altura da imagem, bem como o número de tabelas de quantização de cada componente. A largura e a altura serão usadas para começar a decodificar as digitalizações reais da imagem na seção Início da digitalização. Como trabalharemos principalmente com uma imagem YCbCr, podemos supor que haverá três componentes, e seus tipos serão 1, 2 e 3, respectivamente. Vamos escrever o código para decodificar esses dados:
class JPEG:
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
self.quantMapping = []
with open(image_file, 'rb') as f:
self.img_data = f.read()
# ----
def BaselineDCT(self, data):
hdr, self.height, self.width, components = unpack(">BHHB",data[0:6])
print("size %ix%i" % (self.width, self.height))
for i in range(components):
id, samp, QtbId = unpack("BBB",data[6+i*3:9+i*3])
self.quantMapping.append(QtbId)
def decode(self):
# ----
while(True):
# -----
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Adicionamos um atributo de lista à classe JPEG
quantMappinge definimos um método BaselineDCTque decodifica os dados necessários da seção SOF e coloca o número de tabelas de quantização para cada componente na lista quantMapping. Tiraremos vantagem disso quando começarmos a ler a seção Início da verificação. Esta é a aparência da nossa foto quantMapping:
Quant mapping: [0, 1, 1]
Início da decodificação da varredura
Esta é a "carne" de uma imagem JPEG, ela contém os dados da própria imagem. Chegamos ao estágio mais importante. Tudo o que deciframos antes pode ser considerado um cartão que nos ajuda a decodificar a própria imagem. Esta seção contém a própria imagem (codificada). Lemos a seção e descriptografamos usando os dados já decodificados.
Todos os marcadores começaram com
0xff. Este valor também pode fazer parte da imagem digitalizada, mas se estiver presente nesta seção, será sempre seguido por e 0x00. O codificador JPEG o insere automaticamente, isso é chamado de "enchimento de bytes". Portanto, o decodificador deve removê-los 0x00. Vamos começar com o método de decodificação SOS que contém essa função e nos livrar das existentes 0x00. Em nossa foto na seção com uma varredura, não há0xffmas ainda é uma adição útil.
def RemoveFF00(data):
datapro = []
i = 0
while(True):
b,bnext = unpack("BB",data[i:i+2])
if (b == 0xff):
if (bnext != 0):
break
datapro.append(data[i])
i+=2
else:
datapro.append(data[i])
i+=1
return datapro,i
class JPEG:
# ----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
return lenchunk+hdrlen
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
elif marker == 0xffda:
len_chunk = self.StartOfScan(data, len_chunk)
data = data[len_chunk:]
if len(data)==0:
break
Anteriormente, procurávamos manualmente o final do arquivo quando encontramos um marcador
0xffda, mas agora que temos uma ferramenta que nos permite visualizar sistematicamente todo o arquivo, moveremos a condição de busca do marcador dentro do operador else. A função RemoveFF00apenas é interrompida quando encontra outra coisa em vez de 0x00depois 0xff. O loop é interrompido quando a função encontra 0xffd9, para que possamos pesquisar o final do arquivo sem medo de surpresas. Se você executar este código, não verá nada de novo no terminal.
Lembre-se de que o JPEG divide a imagem em matrizes 8x8. Agora precisamos converter os dados da imagem digitalizada em um fluxo de bits e processá-los em blocos de 8x8. Vamos adicionar o código à nossa classe:
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk +hdrlen
Vamos começar convertendo os dados em um fluxo de bits. Você se lembra que a codificação delta é aplicada ao elemento DC da matriz de quantização (seu primeiro elemento) em relação ao elemento DC anterior? Portanto, inicializamos
oldlumdccoeff, oldCbdccoeffe oldCrdccoeffcom valores zero, eles nos ajudarão a manter o controle do valor dos elementos DC anteriores, e 0 será definido por padrão quando encontrarmos o primeiro elemento DC.
O loop
forpode parecer estranho. self.height//8nos diz quantas vezes podemos dividir a altura por 8 8, e é o mesmo com a largura e self.width//8.
BuildMatrixpegará uma tabela de quantização e adicionará parâmetros, criará uma matriz de transformação de cosseno discreta inversa e nos dará as matrizes Y, Cr e Cb. E a função os DrawMatrixconverte em RGB.
Primeiro, vamos criar uma classe
IDCTe comece a preencher o método BuildMatrix.
import math
class IDCT:
"""
An inverse Discrete Cosine Transformation Class
"""
def __init__(self):
self.base = [0] * 64
self.zigzag = [
[0, 1, 5, 6, 14, 15, 27, 28],
[2, 4, 7, 13, 16, 26, 29, 42],
[3, 8, 12, 17, 25, 30, 41, 43],
[9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
]
self.idct_precision = 8
self.idct_table = [
[
(self.NormCoeff(u) * math.cos(((2.0 * x + 1.0) * u * math.pi) / 16.0))
for x in range(self.idct_precision)
]
for u in range(self.idct_precision)
]
def NormCoeff(self, n):
if n == 0:
return 1.0 / math.sqrt(2.0)
else:
return 1.0
def rearrange_using_zigzag(self):
for x in range(8):
for y in range(8):
self.zigzag[x][y] = self.base[self.zigzag[x][y]]
return self.zigzag
def perform_IDCT(self):
out = [list(range(8)) for i in range(8)]
for x in range(8):
for y in range(8):
local_sum = 0
for u in range(self.idct_precision):
for v in range(self.idct_precision):
local_sum += (
self.zigzag[v][u]
* self.idct_table[u][x]
* self.idct_table[v][y]
)
out[y][x] = local_sum // 4
self.base = out
Vamos analisar a aula
IDCT. Quando extraímos o MCU, ele será armazenado em um atributo base. Em seguida, transformamos a matriz MCU revertendo a varredura em zigue-zague usando o método rearrange_using_zigzag. Finalmente, vamos reverter a transformação discreta do cosseno chamando o método perform_IDCT.
Como você deve se lembrar, a tabela DC é fixa. Não vamos considerar como funciona o DCT, isso está mais relacionado à matemática do que à programação. Podemos armazenar essa tabela como uma variável global e consultar pares de valores
x,y. Decidi colocar a tabela e seu cálculo em uma classe IDCTpara tornar o texto legível. Cada elemento da matriz MCU transformada é multiplicado por um valor idc_variablee obtemos os valores Y, Cr e Cb.
Isso ficará mais claro quando adicionarmos o método
BuildMatrix.
Se você modificar a tabela em zigue-zague para ficar assim:
[[ 0, 1, 5, 6, 14, 15, 27, 28],
[ 2, 4, 7, 13, 16, 26, 29, 42],
[ 3, 8, 12, 17, 25, 30, 41, 43],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
[ 9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54]]
você obtém este resultado (observe os pequenos artefatos):

E se você tiver coragem, pode modificar ainda mais a tabela em zigue-zague:
[[12, 19, 26, 33, 40, 48, 41, 34,],
[27, 20, 13, 6, 7, 14, 21, 28,],
[ 0, 1, 8, 16, 9, 2, 3, 10,],
[17, 24, 32, 25, 18, 11, 4, 5,],
[35, 42, 49, 56, 57, 50, 43, 36,],
[29, 22, 15, 23, 30, 37, 44, 51,],
[58, 59, 52, 45, 38, 31, 39, 46,],
[53, 60, 61, 54, 47, 55, 62, 63]]
Então o resultado será assim:

Vamos completar nosso método
BuildMatrix:
def DecodeNumber(code, bits):
l = 2**(code-1)
if bits>=l:
return bits
else:
return bits-(2*l-1)
class JPEG:
# -----
def BuildMatrix(self, st, idx, quant, olddccoeff):
i = IDCT()
code = self.huffman_tables[0 + idx].GetCode(st)
bits = st.GetBitN(code)
dccoeff = DecodeNumber(code, bits) + olddccoeff
i.base[0] = (dccoeff) * quant[0]
l = 1
while l < 64:
code = self.huffman_tables[16 + idx].GetCode(st)
if code == 0:
break
# The first part of the AC quantization table
# is the number of leading zeros
if code > 15:
l += code >> 4
code = code & 0x0F
bits = st.GetBitN(code)
if l < 64:
coeff = DecodeNumber(code, bits)
i.base[l] = coeff * quant[l]
l += 1
i.rearrange_using_zigzag()
i.perform_IDCT()
return i, dccoeff
Começamos criando uma classe invertida de transformada de cosseno discreta (
IDCT()). Em seguida, lemos os dados no fluxo de bits e os decodificamos usando uma tabela de Huffman.
self.huffman_tables[0]e self.huffman_tables[1]consulte as tabelas DC para luma e chroma, respectivamente, e self.huffman_tables[16]e self.huffman_tables[17]consulte as tabelas AC para luma e chroma, respectivamente.
Depois de decodificar o fluxo de bits, usamos uma função para
DecodeNumber extrair o novo coeficiente DC codificado em delta e adicionar a ele olddccoefficientpara obter o coeficiente DC decodificado em delta .
Em seguida, repetimos o mesmo procedimento de decodificação com os valores AC na matriz de quantização. Significado do código
0indica que alcançamos o marcador de Fim do Bloco (EOB) e devemos parar. Além disso, a primeira parte da tabela de quantização AC nos diz quantos zeros à esquerda temos. Agora, vamos nos lembrar de como codificar os comprimentos da série. Vamos reverter esse processo e pular todos esses bits. IDCTEles recebem zeros explicitamente na classe .
Após decodificar os valores DC e AC para o MCU, convertemos o MCU e invertemos a varredura em zigue-zague chamando
rearrange_using_zigzag. E então invertemos o DCT e aplicamos ao MCU decodificado.
O método
BuildMatrixretornará a matriz DCT invertida e o valor do coeficiente DC. Lembre-se de que esta será uma matriz para apenas uma unidade de codificação mínima de 8x8. Vamos fazer isso para todos os outros MCUs em nosso arquivo.
Exibindo uma imagem na tela
Agora vamos fazer nosso código no método
StartOfScancriar um Tkinter Canvas e desenhar cada MCU após a decodificação.
def Clamp(col):
col = 255 if col>255 else col
col = 0 if col<0 else col
return int(col)
def ColorConversion(Y, Cr, Cb):
R = Cr*(2-2*.299) + Y
B = Cb*(2-2*.114) + Y
G = (Y - .114*B - .299*R)/.587
return (Clamp(R+128),Clamp(G+128),Clamp(B+128) )
def DrawMatrix(x, y, matL, matCb, matCr):
for yy in range(8):
for xx in range(8):
c = "#%02x%02x%02x" % ColorConversion(
matL[yy][xx], matCb[yy][xx], matCr[yy][xx]
)
x1, y1 = (x * 8 + xx) * 2, (y * 8 + yy) * 2
x2, y2 = (x * 8 + (xx + 1)) * 2, (y * 8 + (yy + 1)) * 2
w.create_rectangle(x1, y1, x2, y2, fill=c, outline=c)
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk+hdrlen
if __name__ == "__main__":
from tkinter import *
master = Tk()
w = Canvas(master, width=1600, height=600)
w.pack()
img = JPEG('profile.jpg')
img.decode()
mainloop()
Vamos começar com funções
ColorConversione Clamp. ColorConversionobtém os valores Y, Cr e Cb, converte-os em componentes RGB pela fórmula e, em seguida, gera os valores RGB agregados. Por que adicionar 128 a eles, você pode perguntar? Lembre-se, antes do algoritmo JPEG, o DCT é aplicado ao MCU e subtrai 128 dos valores de cor. Se as cores estavam originalmente no intervalo [0,255], o JPEG irá colocá-las no intervalo [-128, + 128]. Precisamos reverter esse efeito durante a decodificação, então adicionamos 128 ao RGB. Quanto Clampao desempacotamento, os valores resultantes podem sair da faixa [0,255], portanto, os mantemos nesta faixa [0,255].
No método
DrawMatrixfazemos um loop em cada matriz 8x8 decodificada para Y, Cr e Cb, e convertemos cada elemento da matriz em valores RGB. Após a transformação, desenhamos pixels no Tkinter canvasusando o método create_rectangle. Você pode encontrar todo o código no GitHub . Se você executá-lo, meu rosto aparecerá na tela.
Conclusão
Quem diria que para mostrar minha cara você teria que escrever uma explicação de mais de 6.000 palavras. É incrível como os autores de alguns dos algoritmos eram inteligentes! Espero que você tenha gostado do artigo. Aprendi muito enquanto escrevia este decodificador. Não achei que houvesse tanta matemática envolvida na codificação de uma imagem JPEG simples. Da próxima vez, você pode tentar escrever um decodificador para PNG (ou outro formato).
Materiais adicionais
Se você estiver interessado nos detalhes, leia os materiais que utilizei para escrever o artigo, bem como alguns trabalhos adicionais:
- Guia ilustrado para revelação de JPEG
- Um artigo muito detalhado sobre a codificação Huffman em JPEG
- Escrevendo uma biblioteca JPEG simples em C ++
- Documentação para struct em Python 3
- Como o FB aproveitou o conhecimento do JPEG
- Layout e formato JPEG
- Apresentação interessante do DoD sobre JPEG forense