Olá colegas! Não escrevo sobre Habr há cem anos, mas agora chegou a hora. Nesta primavera, ensinei o curso de ML avançado na MADE Big Data Academy do Mail.ru Group; Parece que os ouvintes gostaram, e agora me pediram para escrever não tanto um post publicitário, mas educacional sobre um dos tópicos do meu curso. A escolha foi quase óbvia: como exemplo de um modelo probabilístico complexo, discutimos um modelo SIR epidemiológico extremamente relevante (aparentemente ... mas mais sobre isso depois) que modela a propagação de doenças em uma população. Ele tem tudo: inferência aproximada por meio de métodos Markov Monte Carlo e modelos de Markov ocultos com o algoritmo estocástico de Viterbi e até dados apenas de presença.



Com este tópico, apenas uma pequena dificuldade surgiu: comecei a escrever sobre o que realmente contei e mostrei na palestra ... e de alguma forma rápida e imperceptivelmente vinte páginas de texto (bem, com imagens e código) acumuladas, o que ainda não é estava acabado e não era independente. E se você contar tudo de uma maneira que fique claro a partir do "zero" (não do zero absoluto, é claro), você poderá escrever cem páginas. Então, algum dia eu definitivamente irei escrevê-los, mas por agora apresento a sua atenção a primeira parte da descrição do modelo SIR, na qual podemos apenas colocar um problema e descrever o modelo do seu lado gerador - e se o público respeitado tiver interesse, então será possível Continuar.

Modelo SIR: declaração do problema

Eu amo meus amigos e eles me amam,

Nós somos tão próximos quanto podemos ser.

E só porque realmente nos importamos,

tudo o que recebemos, nós compartilhamos!



Tom Lehrer. Eu entendi de Agnes

Então, vamos descobrir. Informalmente, as premissas básicas do modelo SIR são as seguintes:

• existe uma certa população de pessoas na qual algum vírus terrível pode se espalhar;
• inicialmente, o vírus entra na população de uma forma ou de outra (por exemplo, aparece o primeiro doente), e então as pessoas se infectam umas com as outras;
• SIR , :
  
     ○ Susceptible ( , , .. ),
  
     ○ Infected ( )
  
     ○ Recovered ().

Para simplificar, vamos supor que aqueles que estiveram doentes sempre desenvolvem imunidade e são excluídos do ciclo do vírus na natureza. Conseqüentemente, as transições entre esses estados só podem ser da esquerda para a direita: Susceptível → Infectado → Recuperado.



A tarefa é, na verdade, treinar esse modelo, ou seja, entender algo sobre os parâmetros do processo de infecção a partir dos dados. É fácil entender como os dados se parecem - é simplesmente o número de infectados registrados em cada momento no tempo, que denotaremos pelo vetor$$$\boldsymbol{y}$... Por exemplo, quando dei meu dever de casa no curso sobre coronavírus (era, no entanto, sobre outros modelos), os dados para a Rússia eram assim:

[2,2,2,2,3,4,6,8,10,10,10,10,15,20,25,30,45,59,63,93,114,147,199,253,306,438,438,495,658,840,1036,1264,1534,1836,2337,2777,3548,4149,4731,5389,6343,7497,8672]

Mas quais são os parâmetros deste modelo, como eles interagem entre si e como treiná-los, especialmente em um conjunto de dados tão pequeno, é uma questão mais séria.



Em geral, seguirei o esboço geral do trabalho ( Fintzi et al., 2016 ), no qual algoritmos MCMC são construídos para SIR, SEIR e algumas de suas variantes. Mas em comparação com ( Fintzi et al., 2016 ), simplificarei muito o modelo e sua apresentação. A principal simplificação é que ao invés do tempo contínuo, que é considerado na obra original, consideraremos o tempo discreto, ou seja, ao invés de um processo contínuo que em algum momento gera eventos da forma "infectado" e "recuperado", consideraremos que as pessoas passam por um conjunto de pontos discretos no tempo$$$t=1,\ldots,T$... Essa simplificação nos permitirá, em primeiro lugar, nos livrarmos de muitas dificuldades técnicas e, em segundo lugar, passar do algoritmo de Metrópolis-Hastings em geral para o algoritmo de amostragem de Gibbs, ou seja, não calcular a razão de metrópole, como é necessário fazer em ( Fintzi et al., 2016 ). Se você não entendeu o que acabei de dizer, não se preocupe: não precisaremos disso hoje, e se houver próximas partes, explicarei tudo lá.



Vamos denotar os estados do modelo SIR por S, I e R, respectivamente, e o estado de uma pessoa$$$i$ no momento $$$t$ - através $$$x_i^{(t)}\in\{S, I, R\}$... Ao mesmo tempo, introduziremos imediatamente variáveis ​​para o número total de pacientes que ainda não adoeceram.$$$S^{(t)}$doente $$$I^{(t)}$ e recuperado $$$R^{(t)}$ no momento $$$t$... Homem total que teremos$$$N$então para qualquer um $$$t$ será executado $$$S^{(t)} + I^{(t)} + R^{(t)} = N$... E, como escrevi acima,$$$y^{(t)}$deles são pessoas doentes registradas (testadas).



Os parâmetros desconhecidos do modelo são$$$\boldsymbol\theta = \{\beta, \mu, \rho, \boldsymbol{\pi}\}$Onde:

• $$$\boldsymbol\pi$ - a distribuição inicial dos casos; em outras palavras,$$$x^{(1)}_j\sim \boldsymbol{\pi}$ para cada $$$j$; em nosso modelo simplificado, não vamos treinar$$$\boldsymbol\pi$, mas simplesmente registraremos 1-2 casos no primeiro momento;
• $$$\rho$ - a probabilidade de encontrar uma pessoa infectada na população em geral, ou seja, a probabilidade de uma pessoa $$$x_j$ no momento $$$t$quando $$$x_j^{(t)}=I$, serão detectados por meio de testes e inscritos nos dados $$$y^{(t)}$; em outras palavras, para cada pessoa doente, lançamos uma moeda para determinar se o teste vai encontrar ou não, então o item atual é$$$y_t$ tem uma distribuição binomial com parâmetros $$$I^{(t)}$ e $$$\rho$:

  $$

  $$y^{(t)}\mid I^{(t)}, \rho \sim \mathrm{Binomial}(I^{(t)}, \rho);$$

• $$$\mu$ - a probabilidade de uma pessoa doente se recuperar em uma etapa de tempo, ou seja, a probabilidade de transição de um estado $$$I$ no estado $$$R$;

E $$$\beta$ - Este é o parâmetro mais interessante que mostra a probabilidade de infecção em uma contagem de tempo de uma pessoa infectada . Isso significa que, no modelo, assumimos que todas as pessoas da população "se comunicam" entre si ("comunicação" aqui significa contato suficiente para a transmissão da doença; o coronavírus é transmitido principalmente por gotículas aéreas, mas, é claro, é possível modelar e a propagação de qualquer outra doença; ver, por exemplo, a epígrafe), e a probabilidade de se infectar depende de quantos agora estão infectados, ou seja, do que está$$$I^{(t)}$... Vamos assumir o modelo mais simples, em que a probabilidade de infecção de uma pessoa infectada é$$$\beta$, e todos esses eventos são independentes, o que significa que a probabilidade de permanecer saudável é

$$

$$(1-\beta)^{I^{(t)}}.$$

Na verdade, essas suposições têm muito a discutir. O mais surpreendente aqui, na minha opinião pessoal, é a distribuição binomial para$$$y^{(t)}$... Jogar uma moeda com probabilidade de detectar uma pessoa infectada é absolutamente normal, mas não é muito realista jogarmos essa moeda novamente a cada passo, ou seja, podemos “esquecer” uma pessoa infectada já detectada. Como resultado, o modelo SIR pode (e frequentemente o faz) produzir uma sequência completamente não monotônica$$$\boldsymbol{y}$; Isso é estranho, mas não parece ter um grande impacto no resultado, e seria muito mais difícil modelar esse processo de forma mais realista.



Além disso, é óbvio que este modelo se destina a uma população fechada, onde todos "se comunicam" com todos, então não faz sentido lançá-lo, digamos, para a Rússia com o parâmetro N de cem milhões ou para Moscou com o parâmetro dez milhões (e computacionalmente não funcionará). Uma área importante de extensões e extensões de modelos SIR é dedicada a isso: como adicionar um gráfico mais realista de interações e possíveis infecções; provavelmente falaremos sobre isso na última postagem.



Mas com todas essas simplificações, agora, usando os parâmetros acima, podemos escrever a matriz de probabilidade da transição entre os estados. Essas probabilidades (mais precisamente, especificamente a probabilidade de estar infectado) dependem das estatísticas gerais da população. Vamos designar o vetor de estados de todas as pessoas, exceto$$$x_j$, através $$$\boldsymbol{x}_{-j}$, e estender a mesma notação a todas as outras variáveis; por exemplo,$$$I_{-j}^{(t)}$ É o número de infectados por vez $$$t$, para não mencionar $$$x_j$... Então, para as probabilidades de transição de$$$x_j^{(t-1)}$ em $$$x_j^{(t)}$ Nós temos

$$

$$p\left(x_j^{(t)}=S\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=R\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = \mu,$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - \mu,$$

e em todos os outros casos

$$

$$p\left(x_j^{(t)}\mid x_j^{(t-1)}, \boldsymbol{x}_{-j}^{(t-1)}\right) = 0.$$

O mesmo pode ser escrito mais claramente na forma de uma matriz de probabilidade de transição (a ordem das linhas e colunas é natural, SIR):

$$

$$\left(\begin{matrix} (1 - \beta)^{I_{-j}^{(t-1)}} & 1 - (1 - \beta)^{I_{-j}^{(t-1)}} & 0 \\ 0 & 1 - \mu & \mu \\ 0 & 0 & 1\end{matrix}\right)$$

Para um leitor familiarizado com cadeias de Markov e modelos de Markov, pode parecer que este é apenas um modelo de Markov oculto: há um estado oculto, há uma distribuição clara de observáveis ​​para cada estado oculto, as transições são realmente Markov, ou seja, o próximo estado oculto depende apenas do anterior ... Mas há , como se costuma dizer, há uma ressalva: as probabilidades de transição não podem ser consideradas constantes, elas mudam com a mudança$$$I^{(t)}$e este é um aspecto extremamente essencial do modelo que não pode ser jogado fora.



Portanto, a inferência nesse modelo de repente se torna muito mais difícil do que no modelo oculto de Markov usual (embora nem sempre haja esse dom lá). No entanto, embora a conclusão seja mais complicada, ela ainda está sujeita à mente humana - nas próximas instalações (se houver) vou apenas falar sobre isso. E por hoje, quase o suficiente - agora vamos relaxar um pouco e tentar brincar com este modelo por enquanto em um sentido generativo.

Exemplo de geração de dados

Como grande conhecedor e especialista, um

introvertido entrou em quarentena.

***

“Eu não podia trabalhar em casa”, a

abelha tentou explicar para as minhocas.

***

Kaganov morreu brincando alegremente.

Claro, eu sinto muito por ele, entretanto ...



Leonid Kaganov. Quarentenas

Se os parâmetros do modelo são conhecidos e você só precisa gerar uma trajetória de como se desenvolveria a disseminação da doença na população, não há nada complicado no SIR. O código abaixo gera um exemplo de população de acordo com nosso modelo; afirma que codifiquei como$$$S=0$, $$$I=1$, $$$R=2$... Como avisei, para simplificar, irei supor que no momento$$$t=0$ tem exatamente um doente na população e depois continua.

def sample_population(N, T, true_rho, true_beta, true_mu):
    true_log1mbeta = np.log(1 - true_beta)

    cur_states = np.zeros(N)
    cur_states[:1] = 1
    cur_I, test_y, true_statistics = 1, [1], [[N-1, 1, 0]]

    for t in range(T):
        logprob_stay_healthy = cur_I * true_log1mbeta
        for i in range(N):
            if cur_states[i] == 0 and np.random.rand() < -np.expm1(logprob_stay_healthy):
                cur_states[i] = 1
            elif cur_states[i] == 1 and np.random.rand() < true_mu:
                cur_states[i] = 2

        cur_I = np.sum(cur_states == 1)
        test_y.append( np.random.binomial( cur_I, true_rho ) )
        true_statistics.append([np.sum(cur_states == 0), np.sum(cur_states == 1), np.sum(cur_states == 2)])

    return test_y, np.array(true_statistics).T

N, T, true_rho, true_beta, true_mu = 100, 20, 0.1, 0.05, 0.1
test_y, true_statistics = sample_population(N, T, true_rho, true_beta, true_mu)

Este código fornece não apenas os dados reais $$$\boldsymbol{y}$mas também estatísticas "verdadeiras" $$$S^{(t)}$, $$$I^{(t)}$, $$$R^{(t)}$para que possam ser visualizados. Vamos fazer isso; para parâmetros$$$N=100$, $$$T=20$, $$$\rho=0.1$, $$$\beta=0.2$, $$$\mu=0.3$você pode obter algo assim:







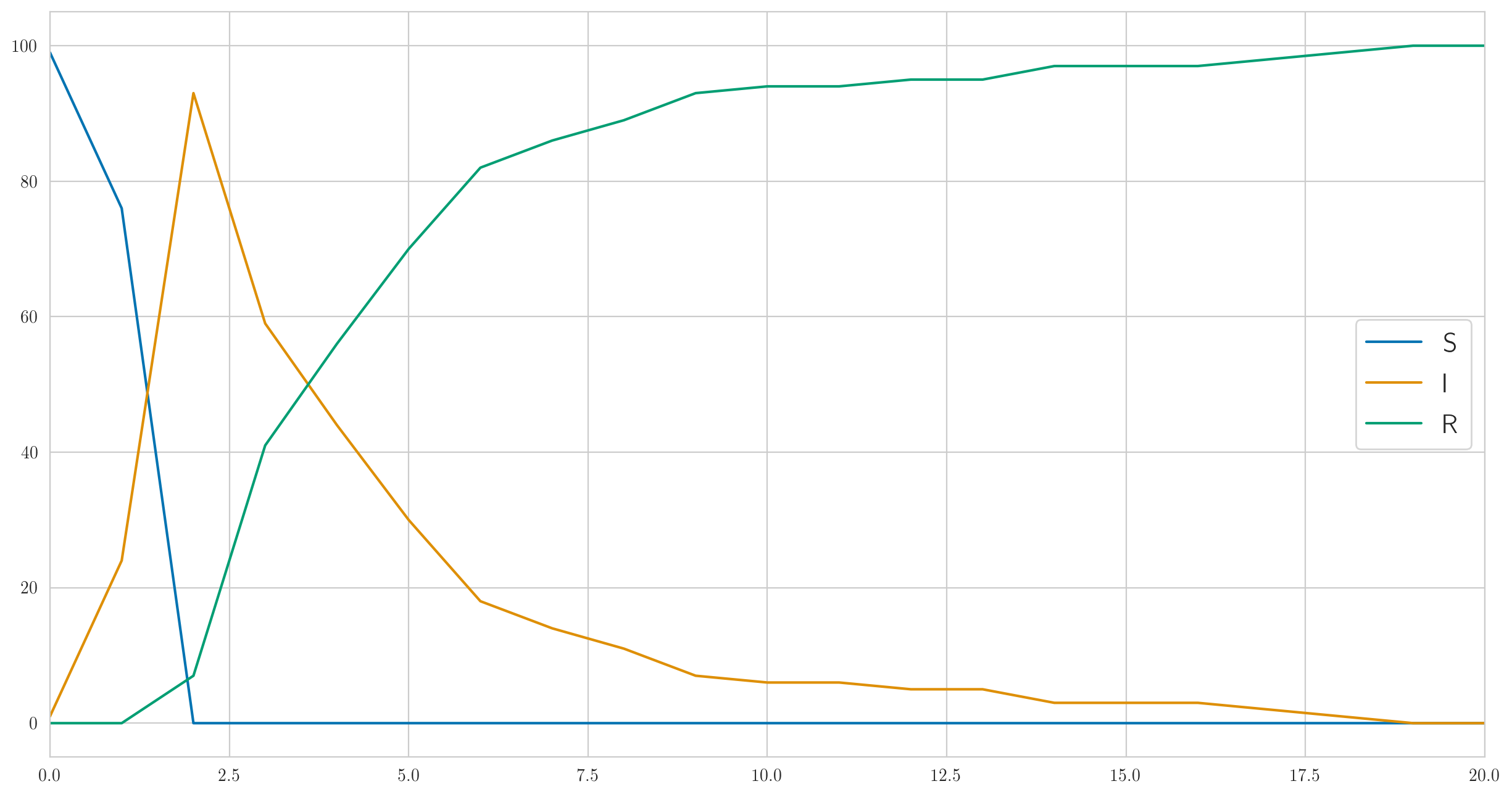
Como você pode ver, neste exemplo, todo mundo fica doente muito rapidamente e, lentamente, começa a melhorar. E os dados reais observados sobre os doentes são assim:

[1 6 13 6 6 4 1 0 0 1 0 1 2 0 0 0 0 0 0 1 0 0]

Observe que, como discutimos acima, não há monotonia aqui.



Mas esse certamente não é o único comportamento possível. Escolhi os parâmetros acima para que a infecção fosse rápida o suficiente e a doença abrangesse quase imediatamente todas as cem pessoas em nossa população de teste. E se você fizer$$$\beta$ menor, por exemplo $$$\beta=0.01$, então a infecção será muito mais lenta e nem todos terão tempo de adoecer antes que o último doente se recupere e não fique. Algo assim:







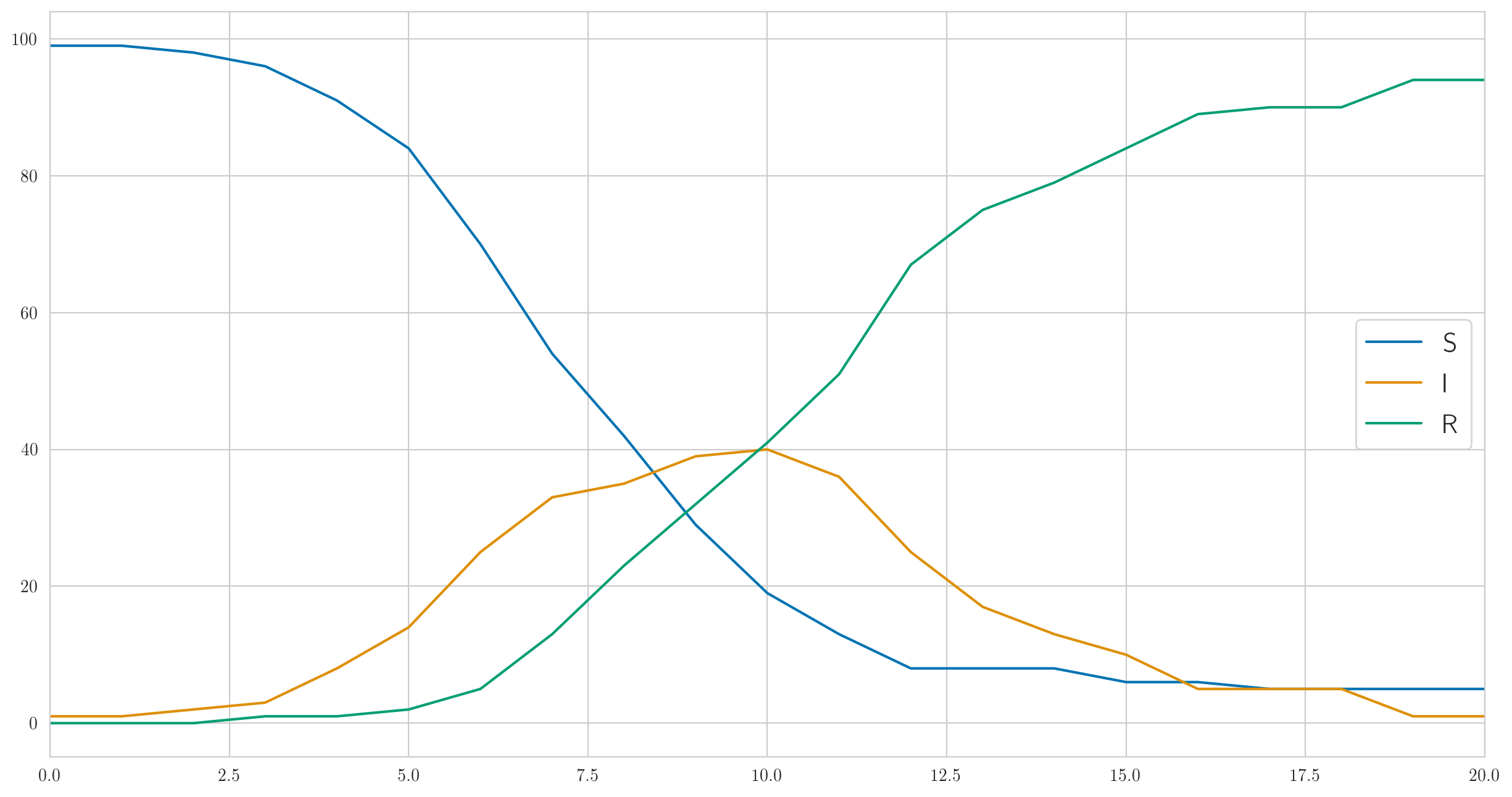
E o número de casos detectados também é completamente diferente:

[1 0 0 0 0 1 2 2 3 1 1 9 3 1 3 1 0 1 0 0 0]

É possível "estrangular" ainda mais a doença; por exemplo, vamos sair$$$\beta=0.01$mas coloque $$$\mu=0.5$, ou seja, a cada intervalo de tempo, cada doente tem uma chance de se recuperar em 0,5 (no final, isso é lógico: ele vai se recuperar ou não). Então, apenas 50-60 em 100 pessoas ficarão doentes com o terrível vírus; curvas podem ser assim:

[1 0 0 1 3 2 1 1 0 3 0 0 0 0 0 1 0 0 0 0 0]

Mas o quadro geral, é claro, em qualquer caso, parece o mesmo: primeiro, crescimento exponencial e depois saturação; a única diferença é se a última operadora tem tempo para se recuperar antes que todos sejam reinicializados.



Bem, é hora de resumir os resultados provisórios. Hoje vimos como é um dos modelos epidemiológicos mais simples. Apesar de muitas suposições simplistas, o modelo SIR ainda é muito útil mesmo nessa forma; o fato é que a maioria de suas extensões são bastante diretas e não mudam a essência geral da questão. Portanto, se continuarmos, na próxima série irei falar sobre como treinar um modelo SIR; no entanto, isso envolverá tantas coisas interessantes que provavelmente não caberá em uma postagem também. Até a próxima vez!