Redes bayesianas com Python - explicadas com exemplos
Devido à informação limitada (especialmente em russo nativo) e aos recursos de trabalho, as redes bayesianas estão cercadas por uma série de problemas. E seria possível dormir bem se não fossem implementadas na maioria das tecnologias avançadas da época, como inteligência artificial e aprendizado de máquina.
Com base nesse fato, este artigo é completamente dedicado ao trabalho das redes bayesianas e como elas mesmas não podem formar problemas, mas ser aplicadas em sua solução, mesmo que os problemas que estão sendo resolvidos sejam extremamente confusos.
Estrutura do artigo
- O que é uma rede bayesiana?
- O que são gráficos acíclicos direcionados?
- Que matemática existe nas redes bayesianas
- Um exemplo que reflete a ideia de uma rede bayesiana
- A essência da rede bayesiana
- Rede bayesiana em Python
- Aplicação de redes bayesianas
Vamos lá.
O que é uma rede bayesiana?
As redes bayesianas se enquadram na categoria de modelos gráficos probabilísticos (GPM). Os VGMs são usados para calcular a variabilidade para aplicação em conceitos de probabilidade.
O nome comum para redes bayesianas é Deep Networks. Eles são usados para modelar gráficos acíclicos direcionados.
O que são gráficos acíclicos direcionados?
Um gráfico acíclico direcionado (como qualquer gráfico em estatística) é uma estrutura de nós e links, onde os nós são responsáveis por alguns valores e os links refletem os relacionamentos entre os nós.
Acíclico == sem ciclos direcionados. No contexto dos gráficos, esse adjetivo significa que, iniciando um caminho a partir de um ponto, não passamos por todo o diagrama do gráfico, mas apenas parte dele. (Ou seja, por exemplo, se começarmos do nó 2 da figura, definitivamente não chegaremos ao nó 1).
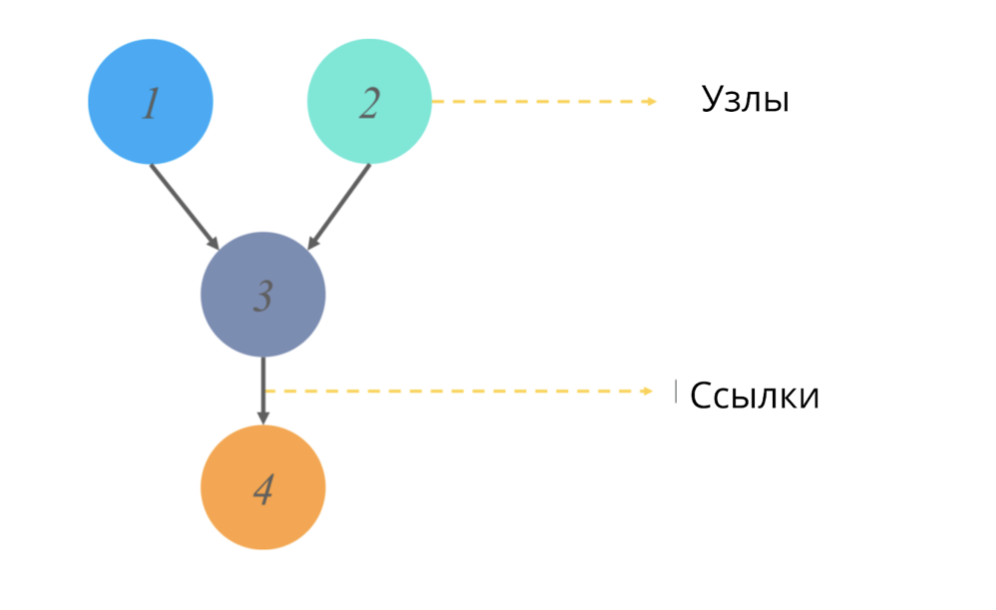
O que esses gráficos simulam e qual valor de saída eles fornecem?
Modelos de gráficos direcionados incertos também são baseados em uma mudança na origem probabilística de um evento para cada um dos valores aleatórios. Uma tabela de probabilidade condicional é aplicável para representar e interpretar cada valor e, portanto, podemos simular a ramificação da probabilidade de eventos seqüenciais.
Tudo bem. Eu também fiquei confuso no começo. Para uma melhor compreensão, vamos analisar o componente matemático das redes bayesianas.
Rede Bayesiana de Matemática
Como já mencionado na definição, as redes bayesianas são baseadas na teoria da probabilidade, portanto, antes de começar a trabalhar com redes bayesianas, duas questões devem ser tratadas:
O que é probabilidade condicional?
Qual é a distribuição de probabilidade média conjunta?
Probabilidade
condicional A probabilidade condicional de algum evento X é o valor numérico da probabilidade de o evento X ocorrer, desde que algum evento Y já tenha ocorrido.
A fórmula de probabilidade padrão para um valor (não fornecido no artigo): P (X) = n (x) / N, em que n são os eventos sob investigação e N são todos os eventos possíveis.
Para dois valores, as seguintes fórmulas se aplicam:
Se X e Y são eventos dependentes:
P (X ou Y) = P (X ⋂ Y) / P (Y), a interseção da probabilidade de X e Y / na probabilidade Y. (O sinal “” no numerador significa a interseção de probabilidades)
Se os eventos X e Y são independentes:
P (X ou Y) = P (X), ou seja, a ocorrência dos eventos em estudo é igualmente provável entre si.
Probabilidade conjunta Probabilidade
conjunta é a definição de uma medida estatística para dois ou mais eventos que ocorrem ao mesmo tempo. Ou seja, os eventos X, Y e, digamos C, ocorrem juntos e refletimos sua probabilidade cumulativa usando o valor P (X ⋂ Y ⋂ C).
Como isso funciona nas redes bayesianas? Vejamos um exemplo.
Um exemplo que reflete a essência da rede bayesiana
Digamos que precisamos modelar a probabilidade de obter uma das notas da nota de um aluno em um exame.
A pontuação é composta por:
- Nível de dificuldade do exame (e): variável discreta com duas gradações (difícil, fácil)
- QI do aluno: variável discreta com duas gradações (baixa, alta)
O valor resultante da avaliação será usado como um preditor (valor preditivo) da probabilidade de uma aluna ou aluna ingressar na universidade.
No entanto, a variável QI também afetará a admissão na admissão.
Representamos todos os valores usando um gráfico acíclico direcionado e uma tabela de distribuição de probabilidade condicional.
Usando essa representação, podemos calcular alguma probabilidade cumulativa, formada a partir do produto das probabilidades condicionais de cinco variáveis.
Probabilidade cumulativa:
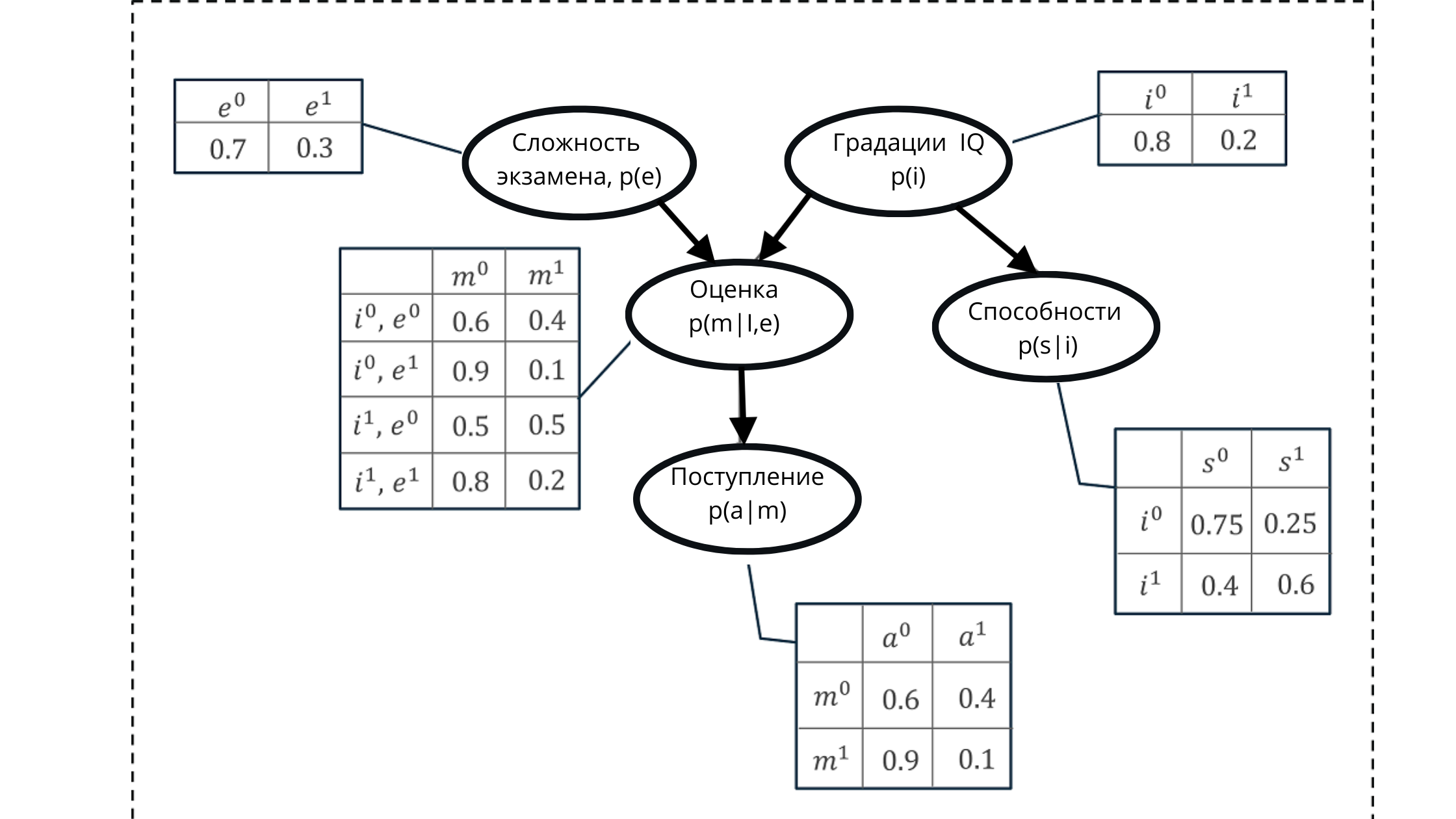
Na ilustração:
p (e) é a distribuição de probabilidade para as notas da variável exame (afeta a nota p (m | i, e)))
p (i) é a distribuição de probabilidade para as notas da variável QI (afeta a nota p (m | i, e )))
p (m | i, e) - distribuição de probabilidade para as séries, com base no nível de QI e na dificuldade do exame (depende de p (i) ep (e))
p (s | i) - coeficientes de probabilidade para as habilidades dos alunos , com base no nível de seu QI (depende da variável QI p (i))
p (a | m) é a probabilidade de matrícula de um aluno na universidade, com base em suas estimativas p (m | i, e)
Aqui, deixe-me lembrá-lo de que a propriedade de um gráfico acíclico é um reflexo relação. Na figura, podemos ver claramente como os nós pais afetam os filhos e como os filhos dependem dos pais.
Daí a formulação do conjunto de valores gerados usando redes bayesianas.
A essência da rede bayesiana
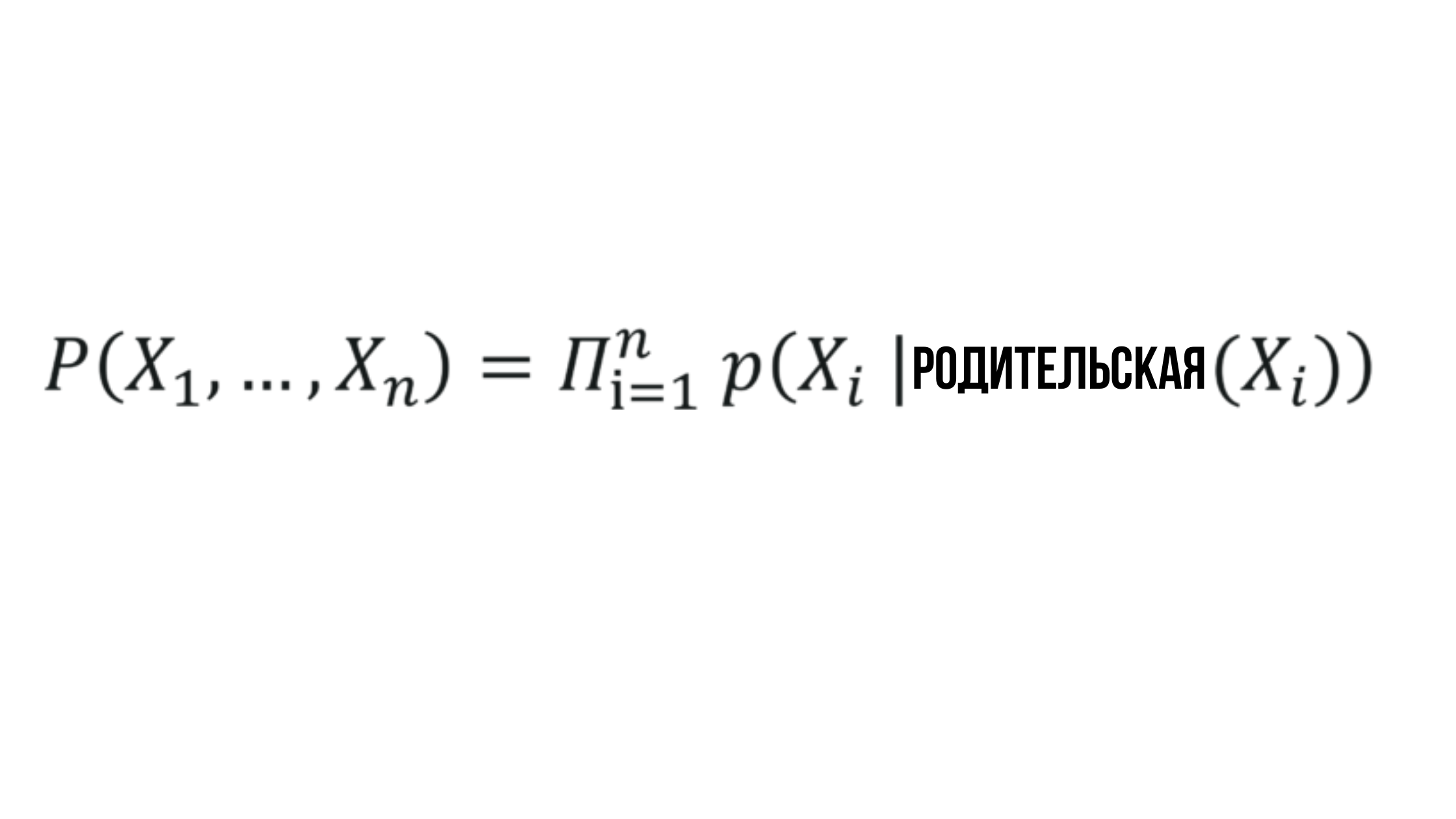
Onde a probabilidade X_i depende da probabilidade do nó pai correspondente e pode ser representada por qualquer valor aleatório.
Parece simples, e com razão - as redes bayesianas são um dos métodos mais simples usados em análise descritiva, modelagem preditiva e muito mais.
Rede Bayesiana em Python
Vejamos a aplicação de uma rede bayesiana a um problema chamado paradoxo de Monty Hall.
Conclusão: imagine que você é um participante do formato de atualização do jogo "Field of Miracles". O tambor não está mais girando - agora você não deve aplicar seu F, mas toque com p.
Há três portas à sua frente, atrás das quais é provável que um carro esteja localizado. As portas, atrás das quais não há carro, levarão você às cabras.
Após a escolha, o líder do restante abre a que leva à cabra (por exemplo, você escolheu a porta 1, o que significa que o líder abre a porta 2 ou 3) e o convida a mudar sua escolha.
Pergunta: o que fazer?
Solução: inicialmente a probabilidade de escolher uma porta com carro = 33% e com cabra = 66%.
- Se você acertar 33%, mudar a porta leva a uma perda => chance de ganhar == 33%
- Se você acertar 66%, a mudança leva a uma vitória => probabilidade de ganhar == 66%
Do ponto de vista da lógica matemática, alterar a porta de maneira agregada leva a uma vitória em 66% por cento e a uma perda em 33%. Portanto, a estratégia correta é mudar a porta.
Mas estamos falando da rede aqui, e pode haver muitas portas, portanto transferiremos a solução para o modelo.
Vamos construir um gráfico acíclico direcionado com três nós:
- Porta do prêmio (sempre com carro)
- Porta selecionável (com carro ou com cabra)
- Porta aberta no evento 1 (sempre com uma cabra)
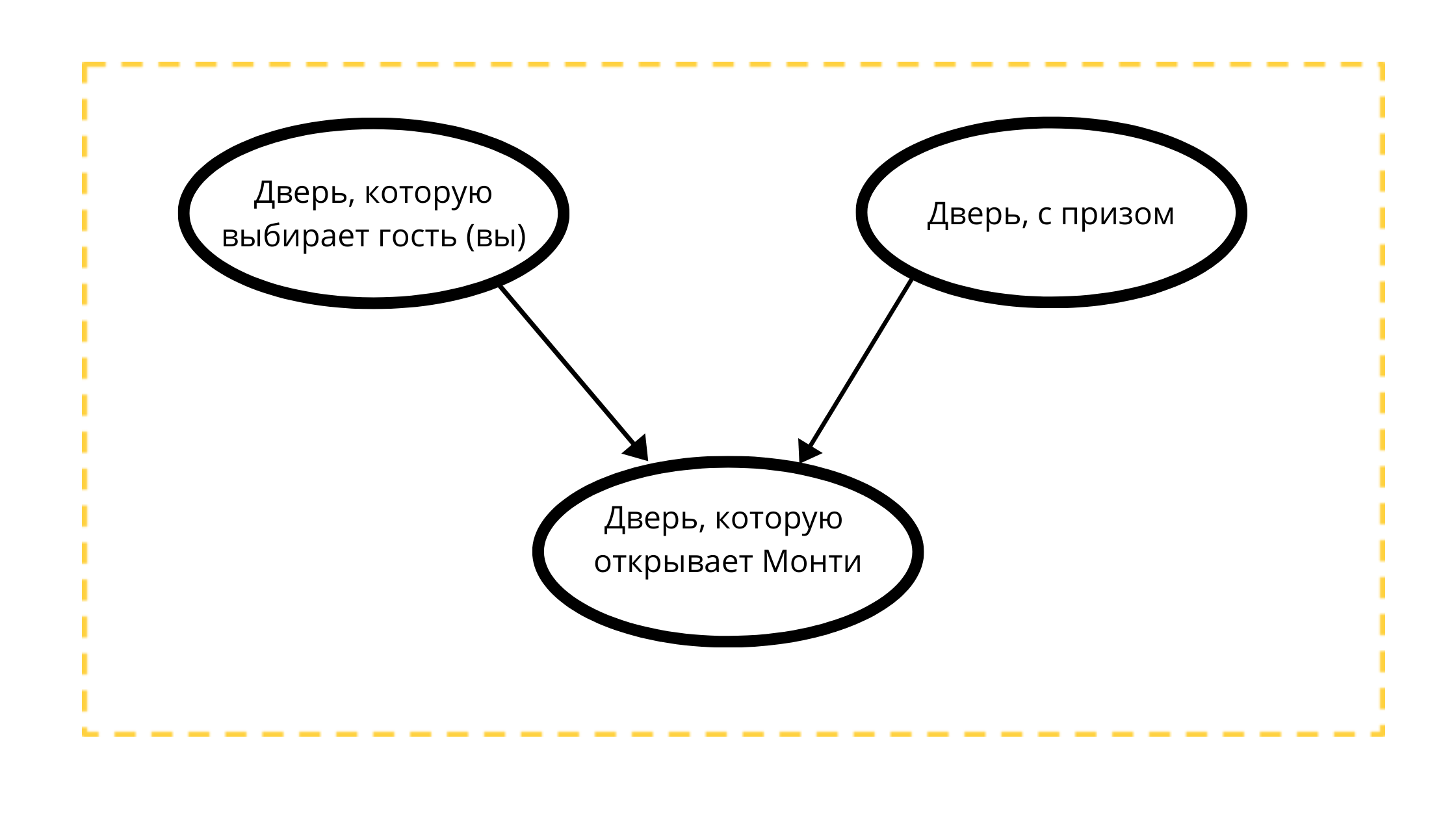
Lendo a contagem:
A porta que Monty abrirá é estritamente influenciada por duas variáveis:
- A porta escolhida pelo hóspede (você) tk Monti 100% NÃO abrirá sua escolha
- Uma porta com um prêmio, talvez Monty sempre abra uma porta sem prêmio.
De acordo com as condições matemáticas do exemplo clássico, o prêmio pode estar igualmente localizado atrás de qualquer uma das portas, assim como você também pode escolher qualquer porta.
#
import math
from pomegranate import *
# " " ( 3)
guest =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
# " " ( )
prize =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
# , ,
#
monty =ConditionalProbabilityTable(
[[ 'A', 'A', 'A', 0.0 ],
[ 'A', 'A', 'B', 0.5 ],
[ 'A', 'A', 'C', 0.5 ],
[ 'A', 'B', 'A', 0.0 ],
[ 'A', 'B', 'B', 0.0 ],
[ 'A', 'B', 'C', 1.0 ],
[ 'A', 'C', 'A', 0.0 ],
[ 'A', 'C', 'B', 1.0 ],
[ 'A', 'C', 'C', 0.0 ],
[ 'B', 'A', 'A', 0.0 ],
[ 'B', 'A', 'B', 0.0 ],
[ 'B', 'A', 'C', 1.0 ],
[ 'B', 'B', 'A', 0.5 ],
[ 'B', 'B', 'B', 0.0 ],
[ 'B', 'B', 'C', 0.5 ],
[ 'B', 'C', 'A', 1.0 ],
[ 'B', 'C', 'B', 0.0 ],
[ 'B', 'C', 'C', 0.0 ],
[ 'C', 'A', 'A', 0.0 ],
[ 'C', 'A', 'B', 1.0 ],
[ 'C', 'A', 'C', 0.0 ],
[ 'C', 'B', 'A', 1.0 ],
[ 'C', 'B', 'B', 0.0 ],
[ 'C', 'B', 'C', 0.0 ],
[ 'C', 'C', 'A', 0.5 ],
[ 'C', 'C', 'B', 0.5 ],
[ 'C', 'C', 'C', 0.0 ]], [guest, prize] )
d1 = State( guest, name="guest" )
d2 = State( prize, name="prize" )
d3 = State( monty, name="monty" )
#
network = BayesianNetwork( "Solving the Monty Hall Problem With Bayesian Networks" )
network.add_states(d1, d2, d3)
network.add_edge(d1, d3)
network.add_edge(d2, d3)
network.bake()No trecho, os valores são:
- A - a porta escolhida pelo hóspede
- B - porta do prêmio
- C - porta escolhida por Monty
No fragmento, calculamos o valor da probabilidade para cada um dos nós do gráfico. Os dois principais nós obedecem em nosso exemplo uma distribuição de probabilidade igual e o terceiro reflete a distribuição dependente. Portanto, para não perder valor, as probabilidades de cada uma das combinações possíveis do jogo são calculadas para .
Após a preparação dos dados, criamos uma rede bayesiana.
É importante notar aqui que uma das propriedades dessa rede é revelar a influência de variáveis ocultas nos observáveis. Ao mesmo tempo, nem as variáveis ocultas nem as observáveis precisam ser especificadas ou determinadas com antecedência - o próprio modelo examina a influência das variáveis ocultas e fará isso com mais precisão quanto mais variáveis receber.
Vamos começar a fazer previsões.
beliefs = network.predict_proba({ 'guest' : 'A' })
beliefs = map(str, beliefs)
print("n".join( "{}t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) ))
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333333,
"B" :0.3333333333333333,
"C" :0.3333333333333333
}
],
}
monty {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"C" :0.49999999999999983,
"A" :0.0,
"B" :0.49999999999999983
}
],
}Vamos analisar o fragmento usando o exemplo da variável A.
Suponha que o convidado a tenha escolhido (A).
O evento “existe um prêmio atrás da porta” na fase de escolha de uma porta por um hóspede tem uma distribuição de probabilidade == ⅓ (já que cada porta pode ter a mesma probabilidade de ser um prêmio).
Em seguida, adicione o valor das probabilidades da porta ser o prêmio no estágio em que a porta é escolhida por Monty. Como não sabemos se a porta do prêmio foi excluída por nossa própria escolha (convidado) na etapa 1, a probabilidade de a porta ser um prêmio nesta fase é 50/50
beliefs = network.predict_proba({'guest' : 'A', 'monty' : 'B'})
print("n".join( "{}t{}".format( state.name, str(belief) ) for state, belief in zip( network.states, beliefs )))
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333334,
"B" :0.0,
"C" :0.6666666666666664
}
],
}
monty B
Nesta etapa, modificaremos os valores de entrada para nossa rede. Agora ele trabalha com a distribuição de probabilidade obtida nas etapas 1 e 2, onde
- as chances de ganhar na porta de nossa escolha não mudaram (33%)
- as chances de ganhar o prêmio na porta aberta por Monty (B) foram canceladas
- as chances de ser um prêmio na porta, deixado sem vigilância, assumiram o valor de 66%
Portanto, como foi concluído acima, a estratégia correta por parte dos convidados para este jogo é mudar a porta - aqueles que mudam a porta matematicamente têm ⅔ chances de ganhar contra aqueles que não mudam a porta (⅓).
No exemplo com três nós, os cálculos manuais são sem dúvida suficientes, mas com um aumento no número de variáveis, nós e fatores de influência, a rede bayesiana é capaz de resolver o problema do valor preditivo.
Aplicação de redes bayesianas
1. Diagnóstico:
- predição baseada em sintomas da doença
- modelagem de sintomas para a doença subjacente
2. Pesquisando na Internet:
- formação de resultados de pesquisa com base na análise do contexto do usuário (intenções)
3. Classificação dos documentos:
- filtros de spam com base na análise de contexto
- distribuição de documentação por categoria / classe
4. Engenharia genética
- modelagem do comportamento de redes de regulação de genes com base nas interconexões e relações dos segmentos de DNA
5. Produtos farmacêuticos:
- monitoramento e valor preditivo de doses aceitáveis
Os exemplos acima são fatos. Para uma compreensão completa, é relevante imaginar em que estágio a criação de uma rede bayesiana está conectada e em quais nós o gráfico que descreve.
O problema do paradoxo de Monty Hall é apenas uma base que nos permite ilustrar o trabalho de cadeias com base em uma combinação de distribuições de probabilidade dependentes e independentes. Espero ter entendido.
PS: Eu não sou um ace de Python e estou apenas aprendendo, então não posso ser responsável pelo código do autor. A publicação deste artigo sobre Habré busca mais liberação no mundo do trabalho intelectual da tradução. Acho que no futuro poderei gerar meus próprios tutoriais - neles ficarei feliz em ver pensamentos construtivos sobre o código.