🎠 🔟 🐘 Guerra Blindada: Projeto Armata. Aberração cromática 🚫 🤱🏿 🤽🏽

Armored Warfare: Project Armata é um jogo de ação e tanque on-line gratuito desenvolvido pela Allods Team, o estúdio de jogos MY.GAMES. Apesar do jogo ser feito no CryEngine, um mecanismo bastante popular com uma boa renderização em tempo real, para o nosso jogo, precisamos modificar e criar muito do zero. Neste artigo, quero falar sobre como implementamos a aberração cromática para a visão em primeira pessoa e o que é.

O que é aberração cromática?

A aberração cromática é um defeito da lente em que nem todas as cores chegam ao mesmo ponto. Isso se deve ao fato de o índice de refração do meio depender do comprimento de onda da luz (ver dispersão ). Por exemplo, é assim que a situação parece quando a lente não sofre de aberração cromática:

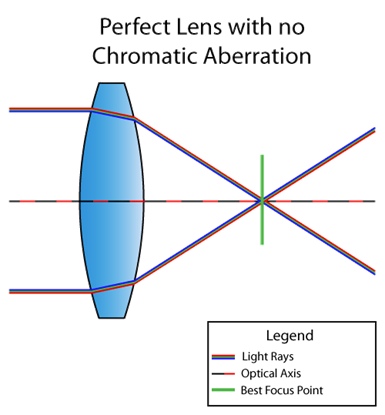
E aqui está uma lente com defeito:

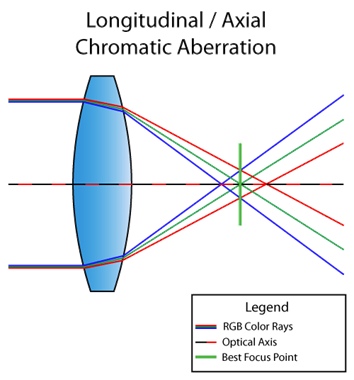
A propósito, a situação acima é chamada de aberração cromática longitudinal (ou axial). Ocorre quando diferentes comprimentos de onda não convergem no mesmo ponto no plano focal após passar pela lente. Em seguida, o defeito é visível em toda a imagem:

Na imagem acima, você pode ver que as cores roxo e verde se destacam devido a um defeito. Não pode ver? E nesta foto?

Há também aberração cromática lateral (ou lateral). Ocorre quando a luz é incidente em ângulo com a lente. Como resultado, diferentes comprimentos de onda da luz convergem em diferentes pontos do plano focal. Aqui está uma imagem para você entender:

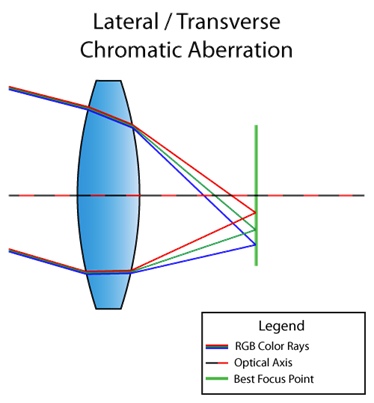
Você já pode ver no diagrama que, como resultado, obtemos uma decomposição completa da luz de vermelho para violeta. Diferentemente da longitudinal, a aberração cromática lateral nunca aparece no centro, apenas mais perto das bordas da imagem. Para que você entenda o que quero dizer, aqui está outra foto da Internet:

Bem, como terminamos a teoria, vamos direto ao ponto.

Aberração cromática lateral com decomposição leve

Começarei com o fato de responder à pergunta que pode surgir na cabeça de muitos de vocês: "O CryEngine não implementou a aberração cromática?" Há sim. Mas é usado no estágio de pós-processamento no mesmo shader com nitidez, e o algoritmo se parece com o seguinte ( link para o código ):

screenColor.r = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 + 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).r;
screenColor.b = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 - 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).b;

O que, em princípio, funciona. Mas temos um jogo sobre tanques. Precisamos desse efeito apenas para a visão em primeira pessoa, e apenas para a beleza, ou seja, para que tudo fique em foco no centro (olá à aberração lateral). Portanto, a implementação atual não se adequava ao menos ao fato de que seu efeito era visível em todo o cenário.

É assim que a aberração se parecia (atenção ao lado esquerdo):

E é assim que ficava se você distorcer os parâmetros:

Portanto, estabelecemos como nosso objetivo:

Implemente a aberração cromática lateral para que tudo fique em foco próximo ao escopo e, se os defeitos característicos da cor não forem visíveis nas laterais, pelo menos fique embaçado.
Prove uma textura multiplicando os canais RGB por coeficientes correspondentes a um comprimento de onda específico. Ainda não falei sobre isso, então agora pode não estar totalmente claro do que se trata este ponto. Mas nós definitivamente consideraremos isso em todos os detalhes posteriormente.

Primeiro, vejamos o mecanismo geral e o código para criar aberrações cromáticas laterais.

half distanceStrength = pow(length(IN.baseTC - 0.5), falloff);
half2 direction = normalize(IN.baseTC.xy - 0.5);
half2 velocity = direction * blur * distanceStrength;

Então, primeiro, uma máscara circular é construída, responsável pela distância do centro da tela, depois a direção do centro da tela é calculada e, em seguida, tudo isso é multiplicado blur. Blure falloff- são parâmetros passados de fora e são apenas multiplicadores para ajustar a aberração. Além disso, um parâmetro é lançado do lado de fora sampleCount, responsável não apenas pelo número de amostras, mas também, de fato, pela etapa entre os pontos de amostragem, pois

half2 offsetDecrement = velocity * stepMultiplier / half(sampleCount);

Agora, basta ir sampleCountuma vez a partir de um determinado ponto da textura, alternando cada vez mais offsetDecrement, multiplicar os canais pelos pesos correspondentes das ondas e dividir pela soma desses pesos. Bem, é hora de falar sobre o segundo ponto do nosso objetivo global.

O espectro visível da luz varia de 380 nm (violeta) a 780 nm (vermelho). E eis que o comprimento de onda pode ser convertido na paleta RGB. Em Python, o código que faz essa mágica se parece com isso:

def get_color(waveLength):
    if waveLength >= 380 and waveLength < 440:
        red = -(waveLength - 440.0) / (440.0 - 380.0)
        green = 0.0
        blue  = 1.0
    elif waveLength >= 440 and waveLength < 490:
        red   = 0.0
        green = (waveLength - 440.0) / (490.0 - 440.0)
        blue  = 1.0
    elif waveLength >= 490 and waveLength < 510:
        red   = 0.0
        green = 1.0
        blue  = -(waveLength - 510.0) / (510.0 - 490.0)
    elif waveLength >= 510 and waveLength < 580:
        red   = (waveLength - 510.0) / (580.0 - 510.0)
        green = 1.0
        blue  = 0.0
    elif waveLength >= 580 and waveLength < 645:
        red   = 1.0
        green = -(waveLength - 645.0) / (645.0 - 580.0)
        blue  = 0.0
    elif waveLength >= 645 and waveLength < 781:
        red   = 1.0
        green = 0.0
        blue  = 0.0
    else:
        red   = 0.0
        green = 0.0
        blue  = 0.0
    
    factor = 0.0
    if waveLength >= 380 and waveLength < 420:
        factor = 0.3 + 0.7*(waveLength - 380.0) / (420.0 - 380.0)
    elif waveLength >= 420 and waveLength < 701:
        factor = 1.0
    elif waveLength >= 701 and waveLength < 781:
        factor = 0.3 + 0.7*(780.0 - waveLength) / (780.0 - 700.0)
 
    gamma = 0.80
    R = (red   * factor)**gamma if red > 0 else 0
    G = (green * factor)**gamma if green > 0 else 0
    B = (blue  * factor)**gamma if blue > 0 else 0
    
    return R, G, B

Como resultado, obtemos a seguinte distribuição de cores:

Em resumo, o gráfico mostra quanto e que cor está contida em uma onda com um comprimento específico. No eixo das ordenadas, obtemos os mesmos pesos dos quais falei anteriormente. Agora, podemos implementar completamente o algoritmo, levando em consideração o indicado anteriormente:

half3 accumulator = (half3) 0;
half2 offset = (half2) 0;
half3 WeightSum = (half3) 0;
half3 Weight = (half3) 0;
half3 color;
half waveLength;
 
for (int i = 0; i < sampleCount; i++)
{
    waveLength = lerp(startWaveLength, endWaveLength, (half)(i) / (sampleCount - 1.0));
    Weight.r = GetRedWeight(waveLength);
    Weight.g = GetGreenWeight(waveLength);
    Weight.b = GetBlueWeight(waveLength);
        
    offset -= offsetDecrement;
        
    color = tex2Dlod(baseMap, half4(IN.baseTC + offset, 0, 0)).rgb;
    accumulator.rgb += color.rgb * Weight.rgb; 
        
    WeightSum.rgb += Weight.rgb;
}
 
OUT.Color.rgb = half4(accumulator.rgb / WeightSum.rgb, 1.0);

Ou seja, a ideia é que quanto mais temos sampleCount, menos passo temos entre os pontos de amostra e mais dispersamos a luz (levamos em conta mais ondas com comprimentos diferentes).

Se ainda não está claro, então vamos olhar para um exemplo específico, ou seja, a nossa primeira tentativa, e vou explicar o que levar para startWaveLengthe endWaveLength, e como as funções serão implementadas GetRed(Green, Blue)Weight.

Montagem de todo o espectro visível

Portanto, no gráfico acima, sabemos a proporção aproximada e os valores aproximados da paleta RGB para cada comprimento de onda. Por exemplo, para um comprimento de onda de 380 nm (violeta) (veja o mesmo gráfico), vemos esse RGB (0,4, 0, 0,4). São esses valores que levamos para os pesos dos quais falei anteriormente.

Agora, vamos tentar nos livrar da função de obter cores por um polinômio do quarto grau, para que os cálculos sejam mais baratos (não somos um estúdio da Pixar, mas um estúdio de jogos: quanto mais baratos os cálculos, melhor). Esse polinômio de quarto grau deve se aproximar dos gráficos resultantes. Para construir o polinômio, usei a biblioteca SciPy:

wave_arange = numpy.arange(380, 780, 0.001)
red_func = numpy.polynomial.polynomial.Polynomial.fit(wave_arange, red, 4)

Como resultado, é obtido o seguinte resultado (dividi em 3 gráficos separados, correspondentes a cada canal separado, para facilitar a comparação com o valor exato):

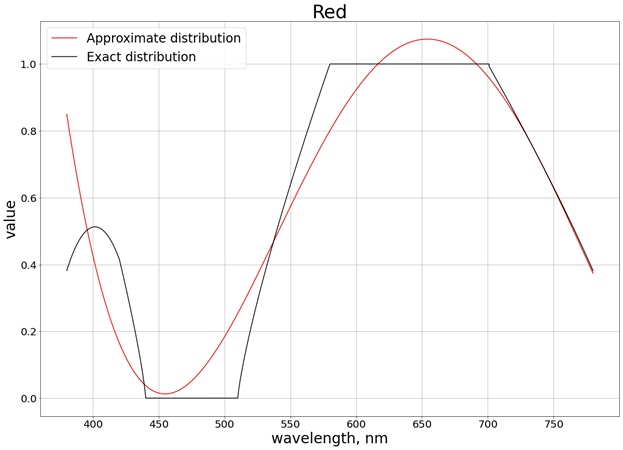
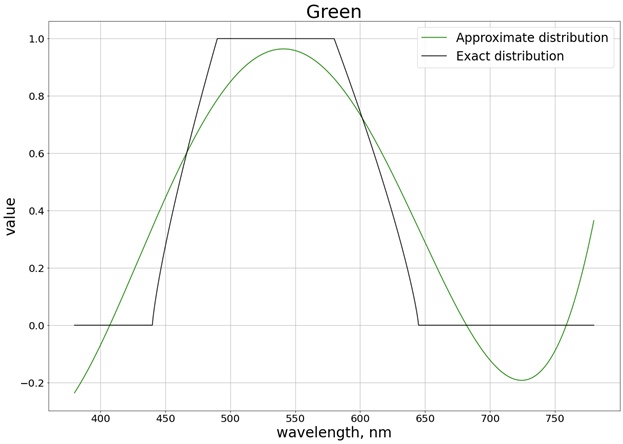
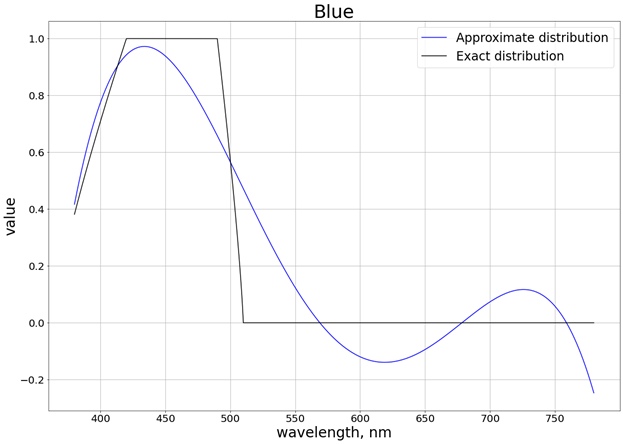
Para garantir que os valores não ultrapassam o limite do segmento [0, 1], usamos a função saturate. Para vermelho, por exemplo, a função é obtida:

half GetRedWeight(half x)
{
    return saturate(0.8004883122689207 + 
    1.3673160565954385 * (-2.9000047500568042 + 0.005000012500149485 * x) - 
    1.244631137356407 * pow(-2.9000047500568042 + 0.005000012500149485 * x, 2) - 1.6053230172845554 * pow(-2.9000047500568042 + 0.005000012500149485*x, 3)+ 1.055933936470091 * pow(-2.9000047500568042 + 0.005000012500149485*x, 4));
}

Os parâmetros ausentes startWaveLengthe endWaveLength, neste caso, são 780 nm e 380 nm, respectivamente. O resultado na prática sampleCount=3é o seguinte (veja as bordas da figura):

Se ajustarmos os valores, aumentar sampleCountpara 400, tudo ficará melhor:

Infelizmente, temos uma renderização em tempo real na qual não podemos permitir 400 amostras (cerca de 3-4) em um shader. Portanto, reduzimos ligeiramente a faixa de comprimento de onda.

Parte do espectro visível

Vamos fazer um intervalo para terminar com as cores vermelho puro e azul puro. Também recusamos a cauda vermelha à esquerda, pois afeta muito o polinômio final. Como resultado, obtemos a distribuição no segmento [440, 670]:

Além disso, não há necessidade de interpolar todo o segmento, pois agora podemos obter um polinômio apenas para o segmento em que o valor muda. Por exemplo, para a cor vermelha, esse é o segmento [510, 580], onde o valor do peso varia de 0 a 1. Nesse caso, você pode obter um polinômio de segunda ordem, que saturatetambém é reduzido pela função para o intervalo de valores [0, 1]. Para todas as três cores, obtemos o seguinte resultado, considerando a saturação:

Como resultado, obtemos, por exemplo, o seguinte polinômio para vermelho:

half GetRedWeight(half x)
{
    return saturate(0.5764348105166407 + 
    0.4761860550080825 * (-15.571636738012254 + 0.0285718367412005 * x) - 
    0.06265740390367036 * pow(-15.571636738012254 + 0.0285718367412005 * x, 2));
}

E na prática com sampleCount=3:

Nesse caso, com as configurações distorcidas, obtém-se aproximadamente o mesmo resultado da amostragem em toda a faixa do espectro visível:

Assim, com polinômios de segundo grau, obtivemos um bom resultado na faixa de comprimento de onda de 440 nm a 670 nm.

Otimização

Além de otimizar os cálculos com polinômios, você pode otimizar o trabalho do sombreador, contando com o mecanismo que estabelecemos na base de nossa aberração cromática lateral, ou seja, não realize cálculos na área onde o deslocamento total não excede o pixel atual, caso contrário, iremos amostrar o mesmo pixel, e nós entendemos.

Se parece com isso:

bool isNotAberrated = abs(offsetDecrement.x * g_VS_ScreenSize.x) < 1.0 && abs(offsetDecrement.y * g_VS_ScreenSize.y) < 1.0;
if (isNotAberrated)
{
    OUT.Color.rgb = tex2Dlod(baseMap, half4(IN.baseTC, 0, 0)).rgb;
    return OUT;
}

A otimização é pequena, mas muito orgulhosa.

Conclusão

A própria aberração cromática lateral parece muito fria; esse defeito não interfere na visão do centro. A idéia de decompor a luz em pesos é um experimento muito interessante que pode fornecer uma imagem completamente diferente se o seu mecanismo ou jogo permitir mais de três amostras. No nosso caso, foi possível não incomodar e criar um algoritmo diferente, pois mesmo com otimizações não podemos pagar muitas amostras e, por exemplo, a diferença entre 3 e 5 amostras não é muito visível. Você pode experimentar o método descrito e ver os resultados.

Guerra Blindada: Projeto Armata. Aberração cromática