O modelo matemático do fenômeno postula que todos os processos ocorrem no espaço-tempo quadridimensional, no qual os fenômenos SRT decorrem da preservação do intervalo de eventos durante a transformação da rotação do sistema de coordenadas. Dificilmente se pode negar que a realidade é estendida sobre construções matemáticas. Além disso, o fato de os números imaginários, na realidade inimagináveis, desempenharem um papel quase inteiramente importante neles, não diminui o sucesso da ciência. Até E. Mach disse que as explicações são supérfluas se os fenômenos observados são bem descritos por fórmulas. E não vamos discutir com essa crítica empírica.
Os matemáticos inventam abstrações e as experimentam na realidade. Daí a singularidade, buracos de minhoca e outras coisas exóticas. Ou talvez valha a pena fantasiar , por exemplo, sobre o que mudaria em nossas idéias sobre o mundo se a causa da contração de Lorentz fosse algum mecanismo físico hipotético. Por que não?
1 a causa física da contração de Lorentz
Primeiro, expressarei a máxima aparentemente óbvia de que partículas, átomos e moléculas interagem entre si através de campos físicos . Podemos, é claro, dizer que eles trocam partículas quânticas, mas agora estamos jogando no campo da teoria relativística, portanto, por enquanto, esqueceremos os quanta. Portanto, a primeira suposição fantástica é que é precisamente devido ao equilíbrio mútuo dos efeitos de campo que as partículas são adicionadas a uma determinada configuração e formam corpos . Se alguma partícula se desviar da posição de equilíbrio, ocorrerá uma perturbação do campo, que moverá o restante das partículas, o que, por sua vez, causará um efeito de campo reverso delas sobre essa partícula.
E a segunda suposição é quea perturbação do campo se propaga em um determinado espaço comum com uma certa velocidade . E a natureza fantástica dessa suposição é que, de acordo com a ciência, o campo existe por si só no espaço-tempo 4-dimensional (P-W) e não se espalha por nada. Em geral, é difícil na ciência ... Vamos supor que os campos se espalhem e existam em um único espaço tridimensional - no qual estamos, a Terra e as estrelas. Parece que isso é óbvio e quem não sabe, mas vamos ver o que acontece. Aqueles que não estão interessados em se preocupar com fórmulas podem limitar-se a ler apenas o texto selecionado.
Então, concordamos que existe um tempo de interação entre as partículas, que é composto pelo tempo de chegada de indignação e pelo tempo de retorno da resposta deles. Como resultado, a configuração anterior do corpo será gradualmente estabelecida novamente. Fig.1 Influências de campo que determinam a posição da partícula
Para qualquer ponto do corpo, é possível distinguir grupos de pontos com os quais ele terá tempos de interação iguais e que chamaremos de isócrono com esse ponto. A situação é refletida na figura 1. Naturalmente, em repouso, a esfera de qualquer raio de repouso R em torno de um ponto é o locus de pontos (GMT) isócrono com ele.
Observe que o movimento de uma partícula em cada momento é determinado pela soma das forças resultantes que são aplicadas simultaneamente da totalidade de todos os grupos de partículas isócronas com ela... Vamos tentar descobrir como a superfície do GMT, formada por um conjunto de pontos 2, 3, etc., mudará quando o corpo se mover. com os mesmos tempos de interação com o ponto 1, que podem não ser mais uma esfera.
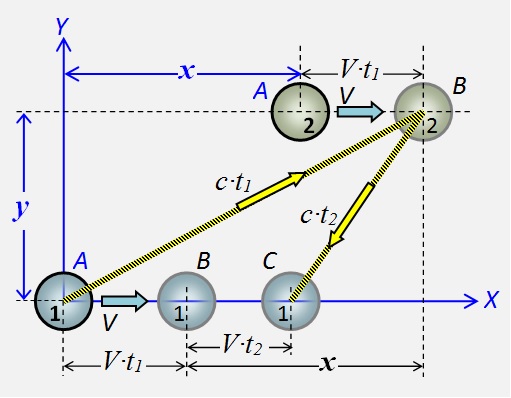Deixe pontos do corpo 1 e 2 são fixas mutuamente e sincronicamente deslocar a direita com a velocidade V . Quando um ponto está na origem, o campo de perturbação é enviado para o ponto 2. O arranjo mútuo dos pontos marcados com a letra A . Fig.2 Esquema das interações de campo dos pontos do corpo - para frente e para trás
Quando a perturbação atinge o ponto 2, ela percorre a distância V ∙ t 1 . Posições pontos marcados com a letra B . Durante o tempo em que a perturbação retornar do ponto 2 ao ponto 1, o ponto 2 cobrirá a distânciaV ∙ t 2 . Sua nova posição está marcada com o C .
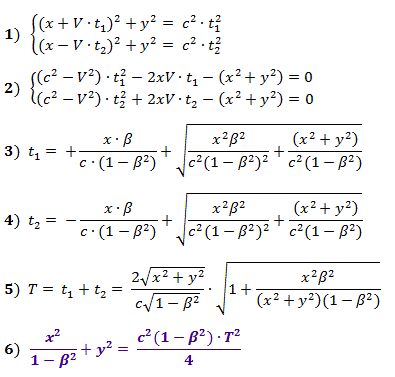As fórmulas (1), de acordo com o teorema de Pitágoras, descrevem as distâncias na Fig. 2, e as obtidas a partir delas (2) são equações para calcular os tempos t 1 e t 2 , cujos valores são dados pelas fórmulas (3) e (4) para valores positivos das raízes, onde β = V / c .
A fórmula (5) fornece o valor do tempo de interação, desde o envio de um distúrbio até o recebimento de uma resposta.
A partir de (5), obtemos a equação (6) para as coordenadas x e y do local geométrico dos pontos isócronos com o qual o tempo de interação do ponto 1 é o mesmo.
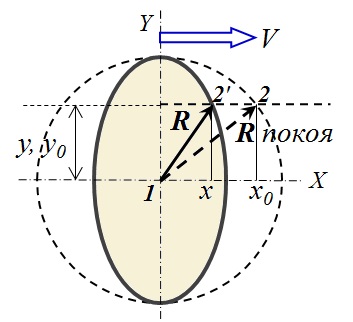A fórmula (6) descreve o elipsóide mostrado na figura 3, comprimido ao longo da direção do movimento (ao longo do eixo X) por √ (1 - β 2 ) vezes, isto é, de acordo com a fórmula de Lorentz. O ponto 2 na superfície da esfera em repouso, enquanto estiver em movimento, passará para a posição 2 ' . Nesse caso, os pontos materiais que eram isócronos com o ponto 1 em repouso permanecerão isócronos durante o movimento . Fig.3
Assim, ao se mover, um objeto material é comprimido de acordo com Lorentz precisamente porque a própria "imagem" dos campos físicos é comprimida, o que garante sua integridade no espaço .
Como a contração de Lorentz é a mesma para todos os pontos isócronos que cercam cada ponto do objeto, então todo o objeto em movimento se contrai proporcionalmente ao longo do eixo do movimento.
2. Derivação da fórmula para dilatação do tempo
Vamos determinar o tempo de interação quando o objeto está se movendo em comparação com o tempo de interação em repouso.
As fórmulas (7) relacionam as coordenadas dos pontos durante o movimento com as coordenadas em repouso, de acordo com a
equação (6). A fórmula (8) calcula o tempo de interação em repouso. Fórmulas (9) e (10) foram obtidas a partir da fórmula (6) por substituição em que os valores das coordenadas x e y e R de resto a partir de fórmulas (7). A fórmula (11) é equivalente a (10). A fórmula (12), obtida de (11) substituindo o lado esquerdo da fórmula (8), conecta os tempos de interação em repouso e durante o movimento. Na forma tradicional, isso se reflete na fórmula (13), em que T 0 é o intervalo de tempo entre os eventos em um objeto em repouso eT é o intervalo de tempo entre os mesmos eventos em um corpo em movimento.
Portanto, os tempos de interação de todos os pontos em um objeto em movimento aumentam na mesma proporção, de acordo com Lorentz, em comparação com o tempo de interação em repouso. Por conseguinte, em geral, todos os processos em um objeto em movimento diminuem a velocidade no mesmo aspecto .
É fácil entender o motivo da desaceleração do tempo, se levarmos em conta que a perturbação do campo pela parte traseira das partículas em interação terá que alcançar a da frente na direção do movimento . Quando a velocidade do corpo é quase igual à velocidade da luz, levará muito tempo para alcançá-lo, e se a velocidade do corpo for igual à velocidade da luz, ela nunca alcançará. Todas as mudanças no corpo vão parar e o tempo parece parar.
3.Explicação do fenômeno da constância da velocidade da luz, etc.
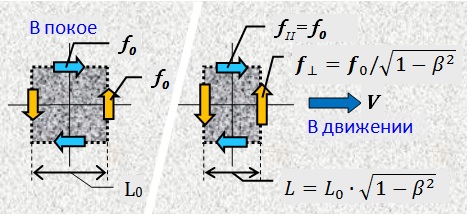
Vamos fazer um experimento mental. Seja emitido um pulso de luz do último vagão do trem, recebido em seu vagão principal. Temos que medir o tempo T 0 que a luz gastará na passagem de um trem de comprimento conhecido L 0 em seu próprio sistema. Na prova, usaremos as suposições sobre a homogeneidade e isotropia do espaço, em particular, assumiremos os mesmos resultados de medição para a primeira e a segunda metade do trem, bem como para as direções para frente e para trás. Mas, estritamente falando, essas suposições são válidas apenas dentro do local e hora do experimento.
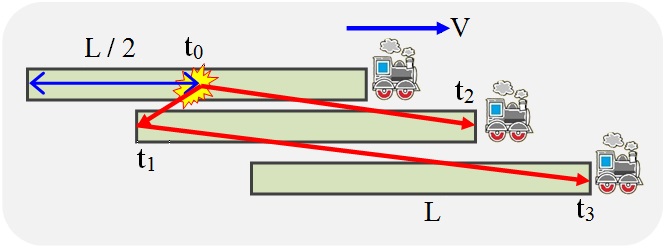
Fig. 4. Experiência para determinar a velocidade da luz em um trem em movimento
Para sincronizar o momento de enviar um sinal do último vagão do trem e o contador do início do tempo no vagão da frente, usamos um pulso de luz inicial do meio do trem para as duas extremidades.
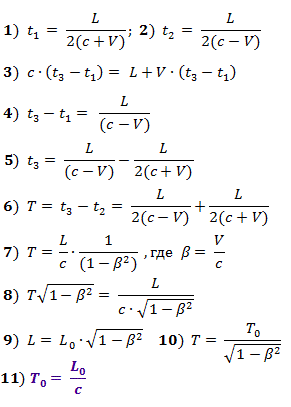
Quando o sinal de partida do meio do trem atingir sua cauda (tempo t 1 ), um pulso de luz será enviado. Quando o sinal de partida chegar à cabeça do trem (tempo t 2 ), a contagem regressiva começará até a chegada do pulso enviado.
Quando a luz viaja para a cauda, sua velocidade é adicionada à velocidade do trem; quando, à cabeça, a velocidade do trem é subtraída. Obtemos as relações dadas abaixo nas fórmulas (1) - (6).
Tempo T = t 3 - t 2 é o intervalo de tempo que,de acordo com o observador no trem , ele separa os eventos do momento de enviar o sinal do final do trem (do momento de receber o sinal de partida ali) e o momento de seu recebimento na cabeceira do trem.
De (6) obtemos a fórmula (7), que transformamos na forma (8). Além disso, levaremos em conta que todas as quantidades L , T e t aqui são medidas no quadro de referência de um observador externo no espaço em que o experimento mental está ocorrendo. Mas quando um objeto se move no espaço, seu comprimento, como provado no Capítulo 1 , na verdade sofre a contração de Lorentz, e os tempos dos eventos, como provado no Capítulo 2, na verdade, desacelere pelo mesmo número de vezes, ou seja, prossiga por mais tempo do que em repouso, refletido nas fórmulas (9) e (10). Substituindo essas proporções na fórmula (8) pelo intervalo T - o tempo de viagem da luz da cauda até a cabeça do trem, obtemos a relação (11).
Mas que relação estes T 0 e L 0 em repouso têm a seu próprio tempo e comprimento para os mesmos eventos, medido no referencial inercial (IRF) associado a um trem em movimento? Obviamente eles são iguais . O fato é que o tempo e a duração são expressos numericamente através de sua relação com os padrões. Consequentemente, as medidas das coordenadas temporais e espaciais de algo feito em repouso serão numericamentesão iguais às medidas do mesmo, feitas em um ISO em movimento, pois ao mover os valores de ambas as medidas e padrões mudam proporcionalmente.
A questão é como exatamente eles mudam quando se deslocam no espaço. Um experimento mental com um trem prova que eles mudam de tal maneira que o valor numérico da velocidade da luz medida em IFR permanece igual ao valor de sua velocidade no espaço . É precisamente isso que não era a priori uma prova óbvia e necessária.
Vemos que o "postulado da constância da velocidade da luz" deriva apenas do fato da contração de Lorentz, que é matematicamente derivada da dependência da localização da matéria material na velocidade de propagação e configuração dos campos físicos no espaço .
Para completar a imagem, também definimos a velocidade da luz através do movimento do trem, por exemplo, entre as paredes da carruagem, a uma distância S 0 uma da outra. Para fazer isso, medimos o tempo de movimento do pulso de luz ( 2 · t 0 ) para frente e para trás. Em vista da simetria óbvia de "lá" e "de volta", consideraremos apenas "lá". No sistema de um observador externo, o movimento no espaço ocorre como mostrado na Fig. 5.
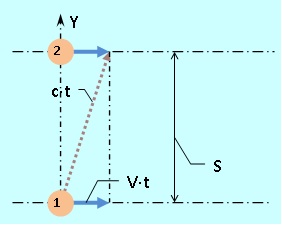Portanto, temos (c · t) 2 = S 2 + (V · t) 2 , de onde obtemos t = S / (c · √ (1 - β²)) , onde β = V / c .
No sistema de trens, o tempo adequado decorrido t 0ligado ao tempo passado no espaço pela relação t = t 0 / (√ (1 - β²)) . Substituindo essa expressão na fórmula de t no espaço, obtemos t 0 = S / c .
Fig. 5. Experiência para determinar a velocidade da luz em um trem em movimento /
No sistema do trem para o mesmo t 0, temos a relação t 0 = S 0 / c 0 . Mas como as dimensões transversais não mudam durante o movimento, ou seja, S = S 0 , obtemos que c 0 = c .
Suponho que não há necessidade de provar a constância da velocidade medida da luz para uma orientação arbitrária do feixe, o que apenas acrescentaria complexidade desnecessária. Considerando a comprovada invariância da velocidade da luz, é fácil derivar as transformações de Lorentz (L), e sem apelo às equações de Maxwell ou ao espaço matematicamente abstrato de Minkowski.
4. Derivação das transformações de Lorentz
O evento consiste na chegada de um pulso de luz no ponto " E ",
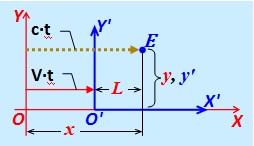localizado nas coordenadas inalteradas x ' e y' no sistema de referência {X ', Y'}, movendo-se com uma velocidade V relativa ao IFR fixo {X, Y}, enviado no momento em que os pontos O e O 'de ambos os COs coincidiram. Fig. 6.
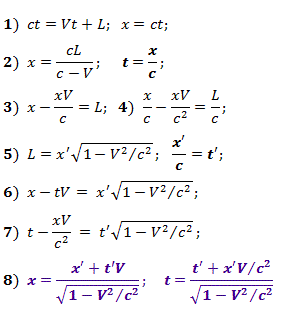No seu próprio comprimento L {X ', Y'} L , medido em CO {X, Y}, a coordenada x ' corresponderá . Para o evento, o sistema de equações (1) é válido, resolvendo o que obtemos (2) e depois (3) e (4).
Uma vez que os comprimentos dos corpos em movimento são comprimidos de acordo com Lorentz, e a velocidade da luz, como provado no capítulo 3 , é a mesma em qualquer FR, então para x ' apropriadoet ' nas relações {X', Y '} (5) são válidas. Substituindo as relações de (5) em (3), obtemos (6) e, substituindo-as em (4), obtemos (7). Em virtude da relatividade do movimento, podemos considerar o sistema em movimento {X, Y}, mas em (6) e (7) é necessário substituir as variáveis não sombreadas pelas sombreadas, e a velocidade V deve ser tomada com o sinal oposto, ou simplesmente resolver o sistema com relação a x e t .
Como resultado, obtemos expressões (8) para a forma canônica de transformações de Lorentz de coordenadas e tempo de eventos em diferentes IFRs.
Ao usar o PL como um método matemático puramente formal, o mecanismo físico dos fenômenos SRT permanece não manifesto. Portanto, em meus artigos anteriores sobre o efeito Doppler relativísticoeaberrações de luz , bem como as leis de reflexão de um espelho inclinado em movimento , as SLs não foram usadas em princípio para demonstrar as razões físicas para esses fenômenos.
5. Justificação do princípio da relatividade e limitações da sua aplicabilidade
Observe que se em repouso no diagrama da Fig. 1 a perturbação do ponto 1 até o GMT dos pontos isócronos ocorreu simultaneamente, ao se mover, no diagrama da Fig. 2, isso não é mais cumprido. Em cada ponto deste GMT, a resposta à perturbação será criada em momentos diferentes, mas eles convergirão no ponto 1 simultaneamente . A questão é: o resultado será o mesmo que em repouso?
Ficou provado acima que, em qualquer IFR, os tempos e distâncias adequados medidos entre todos os pontos serão os mesmos que em repouso . Conseqüentemente, o número de períodos, por exemplo, iniciadoonda eletromagnética entre quaisquer pontos será a mesma que em repouso. Como a perturbação de um campo de uma configuração arbitrária pode ser representada por uma expansão em uma série de harmônicas monocromáticas, as configurações e intensidades de todos os campos no sistema intrínseco serão as mesmas em repouso, respectivamente. Conseqüentemente, as relações de fase e a sincronização dos campos que formam o corpo não são violadas e todos os processos nele ocorrem como durante o descanso.
É exatamente isso que o "princípio da relatividade" de Einstein proclama, e, como vemos, é matematicamente inevitavelmente deduzido de duas suposições (veja o Capítulo 1), deixe-me lembrá-lo: primeiro : que a posição das partículas reais é determinada pela estrutura dos campos e , segundo , quea propagação do campo ocorre a uma velocidade finita .
Ou seja, o princípio da relatividade já é, por assim dizer, não a priori um princípio universal , mas uma conseqüência e possui limites claros de aplicabilidade . Em particular, a velocidade da luz não tem o significado de uma constante mundial, mas é uma velocidade específica da luz em uma região específica do espaço . E em alguns lugares, pode ser diferente devido à interação com campos físicos locais, por exemplo, gravidade. Portanto, temos duas alternativas que resultam exatamente nas mesmas fórmulas relativísticas:
- primeiro, ortodoxo e científico: requer postular a priori o verdadeiro princípio da relatividade ;
- : ,
No primeiro caso, os fenômenos da SRT não requerem explicação e suas causas e mecanismos permanecem desconhecidos. A pergunta "Por quê?" acaba por estar fora da ciência.
No segundo , as suposições são até bastante lógicas e não é necessário postular, e são "fantásticas" apenas na medida em que outras razões para o relativismo sejam aceitas na ciência. Para a pergunta "por que os fenômenos SRT são assim?" aqui é dada uma explicação clara e até quase trivial. Mas há uma necessidade urgente de descobrir a natureza da matéria e em que relação ela está com os campos físicos.
Portanto, continuaremos a fantasiar ainda mais.
6. Derivação da fórmula E = Mc² e as equações da dinâmica
Primeiro, vamos descobrir como as forças são transformadas em velocidades relativísticas. Vamos selecionar o elemento de volume no corpo no qual atuam os momentos equilibrados das forças. Quando o corpo se move, o tamanho longitudinal (ao longo da trajetória de movimento) do elemento selecionado
diminui de acordo com o coeficiente de Lorentz. Para que o elemento permaneça em equilíbrio, as forças perpendiculares ao movimento devem aumentar exatamente na mesma proporção. Fig. 7.
A magnitude das forças paralelas ao movimento não mudará. O fator de dependência das forças na orientação em relação à direção do movimento deve ser levado em consideração na expansão vetorial das forças nas seguintes fórmulas.
Observe que a aceleração do corpo para uma determinada velocidade é realizada pela força aplicada, que, consequentemente, realiza algum trabalho, aumentando assim a energia do corpo. EQual é a diferença entre um corpo disperso no espaço e um corpo em repouso? O fato de o overclock ser comprimido de acordo com Lorentz . No Capítulo 1, é derivada uma fórmula para o local dos pontos (GMT) em torno de um determinado ponto, a partir do qual eles têm o mesmo tempo de interação dos campos físicos. Este GMT acaba por ser um elipsóide comprimido de acordo com Lorentz na direção do movimento. Vamos agora prestar atenção ao fato de que o volume W deste elipsóide diminui proporcionalmente à contração de Lorentz. Isso se reflete na fórmula (1) abaixo. Agora vamos supor realmente que, quando um corpo é acelerado, o trabalho da força é gasto na compressão do volume de espaço que ocupa, que permanece inalterado em livre circulação. Pelo menos, essa suposição não é pior que a máxima científica de que o espaço pode dobrar ou inchar.
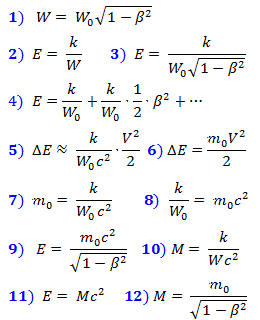Suponha que essa energia E seja inversamente proporcional ao volume ao qual foi possível compactá-la de acordo com a fórmula (2) ou (3) após a substituição (1) nela. Expandimos
E de (3) para uma série de Taylor (4), de onde (5) é o incremento de energia da velocidade na primeira aproximação em baixas velocidades. Mas em baixas velocidades também é igual a (6). Comparando (5) e (6), obtemos (7) e (8). Substituindo (8) em (3), obtemos (9), que conecta a energia de um corpo no espaço comprimido com sua massa de repouso.
Vamos expressar a massa relativística pela fórmula (10), de onde, substituindo (2), obtemos a expressão bem conhecida (11), que relaciona massa e energia. Comparando (9) e (11), obtemos (12).
A massa é apenas outra formulação da energia gasta no espaço de compressão. E nesse sentido eles são equivalentes. E a substância apenas "marca" a área do espaço ocupado pelo corpo.
Alteração na energia total E do sistema, ou seja, a energia de compressão do espaço, em total conformidade com a mecânica clássica newtoniana, é igual ao trabalho da força aplicada como produto da força por caminho, e a mudança no momento P do sistema é igual ao produto da mesma força e do tempo de sua ação. Essas dependências são refletidas nas fórmulas (13). Depois de substituir neles as expressões para a energia de (11) e o momento Pda fórmula (14)
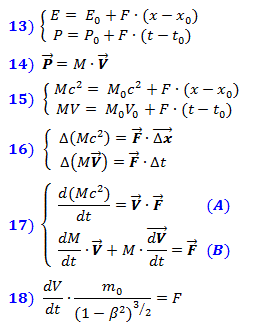obtemos o sistema de equações (15), que é escrito na forma de pequenos incrementos em (16) na forma vetorial. Então, diferenciando-se em relação ao tempo, escrevemos o sistema de equações diferenciais (17) que descreve a dinâmica relativística. A força F não precisa ser diferenciada, pois é externa e não depende das variações das variáveis do sistema. Substituindo a expressão de massa de (12) na fórmula ( A ), obtemos a conhecida fórmula relativística para o movimento retilíneo (18). 
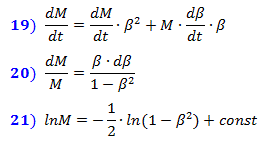A partir do sistema de equações (17) é possível descobrir a dependência da massa em relação à velocidade. Substituindo F da fórmula ( B ) na fórmula ( A ) e dividindo os dois lados da igualdade por c², ao acelerar ao longo da trajetória do movimento, obtemos expressões (19) e (20). De onde, integrando, obtemos expressão (21). É fácil ver que é equivalente à expressão logarítmica (12) para a massa relativística, onde const é igual ao logaritmo da massa restante m 0 . Isso significa que apenas essa dependência da massa da velocidade garante a correspondência da energia Mc² e do momento M · V , nas fórmulas (16, 17). E a partir daqui também se segue que o valor que assumimos anteriormente como a massa restante é uma constante independente da velocidade, como está escrito nas fórmulas originais (9). E isso significa que nossa suposição sobre a dependência de energia no grau de compressão do espaço está correta.
Obviamente, a reivindicação de compactação do espaço não é muito convincente. Se o espaço deveria ser um recipiente vazio de partículas e corpos, como você pode comprimir o vazio? O vazio permanecerá vazio. A ciência, no entanto, permite-se falar sobre a curvatura do espaço vazio - as fórmulas exigem isso. No entanto, estritamente falando, seu espaço é uma abstração matemática.
Mas podemos razoavelmente assumir que o espaço não está vazio, mas preenchido com algum tipo de matéria que, suponha, não em estado comprimido, é percebida por nós como um vazio.... Quando, por exemplo, está sob tensão de compressão, temos corpos e partículas de material. Quando estão em repouso, o grau de compressão (energia) de uma seção dessa matéria corresponde à massa restante do corpo e, com sua aceleração, o grau de compressão (energia) do corpo e a massa correspondente aumentam.
E nesse ambiente material, os campos físicos que determinam a localização e a interação das partículas (até os primários "muito-muito" - que, continuamos a fantasiar , serão o fenômeno de focar os campos em seu ambiente sem o qual eles não existem) podem existir e se propagar a uma velocidade específica ), cuja energia de repouso e movimento é determinada pelo grau de compressão da área da matéria primária ocupada por eles . Na realidade,as equações da dinâmica relativística apenas descrevem o movimento dessas tensões nas homogeneidades (corpos materiais) na matéria prima . Como pudemos ver, não há contradições com o experimento de Michelson e as transformações de Lorentz.