
Fonte: unsplash.com
Segundo Jackie Stewart, tricampeão mundial de Fórmula 1, entender o carro o ajudou a se tornar um piloto melhor: "Um piloto não precisa ser engenheiro, mas sim interesse em mecânica ".
Martin Thompson (criador do LMAX Disruptor ) aplicou esse conceito à programação. Em poucas palavras, entender o hardware subjacente aprimorará suas habilidades quando se trata de projetar algoritmos, estruturas de dados e assim por diante.
A equipe do Mail.ru Cloud Solutions traduziu um artigo que se aprofundou no design do processador e analisou como o entendimento de alguns dos conceitos de CPU pode ajudá-lo a tomar melhores decisões.
O básico
Os processadores modernos são baseados no conceito de multiprocessamento simétrico (SMP). Um processador é projetado de forma que dois ou mais núcleos compartilhem uma memória comum (também chamada de memória de acesso principal ou aleatória).
Além disso, para acelerar o acesso à memória, o processador possui vários níveis de cache: L1, L2 e L3. A arquitetura exata depende do fabricante, modelo da CPU e outros fatores. Na maioria das vezes, no entanto, os caches L1 e L2 operam localmente para cada núcleo, enquanto o L3 é compartilhado em todos os núcleos.

Arquitetura SMP
Quanto mais próximo o cache do núcleo do processador, menor a latência de acesso e o tamanho do cache:
| Cache | Demora | Ciclos de CPU | O tamanho |
| L1 | ~ 1,2 ns | ~ 4 | Entre 32 e 512 KB |
| L2 | ~ 3 ns | ~ 10 | Entre 128 KB e 24 MB |
| L3 | ~ 12 ns | ~ 40 | Entre 2 e 32 MB |
Novamente, os números exatos dependem do modelo do processador. Para uma estimativa aproximada, se o acesso à memória principal demorar 60 ns, o acesso ao L1 é cerca de 50 vezes mais rápido.
No mundo do processador, existe um conceito importante de localidade do link . Quando o processador acessa um local de memória específico, é muito provável que:
- Ele se referirá ao mesmo local da memória em um futuro próximo - esse é o princípio da localidade temporal .
- Ele se referirá às células de memória localizadas nas proximidades - este é o princípio da localidade por distância .
A localidade de horário é um dos motivos dos caches da CPU. Mas como você usa a localidade à distância? Solução - em vez de copiar uma célula de memória para os caches da CPU, a linha de cache é copiada para lá. Uma linha de cache é um segmento contíguo da memória.
O tamanho da linha de cache depende do nível do cache (e novamente do modelo do processador). Por exemplo, aqui está o tamanho da linha de cache L1 na minha máquina:
$ sysctl -a | grep cacheline
hw.cachelinesize: 64
Em vez de copiar uma única variável no cache L1, o processador copia um segmento contíguo de 64 bytes lá. Por exemplo, em vez de copiar um único elemento int64 de uma fatia Go, ele copia esse elemento mais mais sete elementos int64.
Usos específicos para linhas de cache no Go
Vejamos um exemplo concreto que demonstra os benefícios dos caches de processador. No código a seguir, adicionamos duas matrizes quadradas de elementos int64:
func BenchmarkMatrixCombination(b *testing.B) {
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i++ {
for j := 0; j < matrixLength; j++ {
matrixA[i][j] = matrixA[i][j] + matrixB[i][j]
}
}
}
}
Se for
matrixLengthigual a 64k, produz o seguinte resultado:
BenchmarkMatrixSimpleCombination-64000 8 130724158 ns/op
Agora, em vez disso,
matrixB[i][j]adicionaremos matrixB[j][i]:
func BenchmarkMatrixReversedCombination(b *testing.B) {
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i++ {
for j := 0; j < matrixLength; j++ {
matrixA[i][j] = matrixA[i][j] + matrixB[j][i]
}
}
}
}
Isso afetará os resultados?
BenchmarkMatrixCombination-64000 8 130724158 ns/op
BenchmarkMatrixReversedCombination-64000 2 573121540 ns/op
Sim, e radicalmente! Como isso pode ser explicado?
Vamos tentar desenhar o que está acontecendo. O círculo azul indica a primeira matriz e o círculo rosa indica a segunda. Quando configuramos
matrixA[i][j] = matrixA[i][j] + matrixB[j][i], o ponteiro azul está na posição (4.0) e o rosa está na posição (0.4):
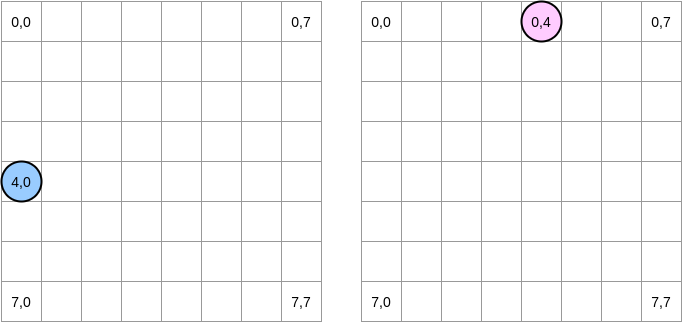
Nota . Neste diagrama, as matrizes são apresentadas em forma matemática: com uma abcissa e uma ordenada, e a posição (0,0) está no quadrado superior esquerdo. Na memória, todas as linhas da matriz são organizadas seqüencialmente. No entanto, por uma questão de clareza, vejamos a representação matemática. Além disso, nos exemplos a seguir, o tamanho da matriz é um múltiplo do tamanho da linha de cache. Portanto, a linha de cache não será "atualizada" na próxima linha. Parece complicado, mas os exemplos deixarão tudo claro.
Como vamos iterar sobre matrizes? O ponteiro azul se move para a direita até atingir a última coluna e depois para a próxima linha na posição (5,0) e assim por diante. Por outro lado, o ponteiro rosa se move para baixo e depois passa para a próxima coluna.
Quando o ponteiro rosa atinge a posição (0,4), o processador armazena em cache a linha inteira (no nosso exemplo, o tamanho da linha do cache é de quatro elementos). Então, quando o ponteiro rosa atinge a posição (0,5), podemos assumir que a variável já está presente em L1, certo?
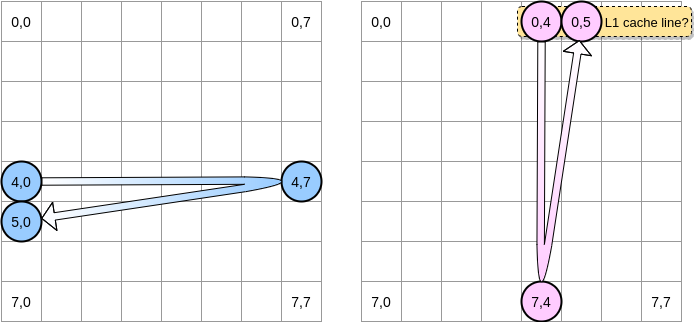
A resposta depende do tamanho da matriz :
- Se a matriz for pequena o suficiente em comparação com o tamanho de L1, sim, o elemento (0.5) já estará em cache.
- Caso contrário, a linha de cache será removida de L1 antes que o ponteiro atinja a posição (0,5). Portanto, ele gerará uma falta de cache e o processador precisará acessar a variável de uma maneira diferente, por exemplo, via L2. Estaremos neste estado:
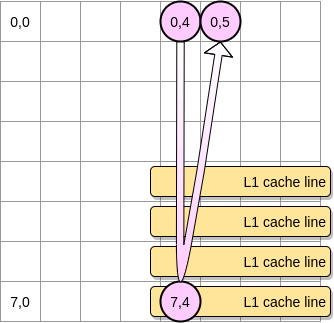
Quão pequena uma matriz precisa ser para se beneficiar de L1? Vamos contar um pouco. Primeiro, você precisa saber o tamanho do cache L1:
$ sysctl hw.l1dcachesize
hw.l1icachesize: 32768
Na minha máquina, o cache L1 tem 32.768 bytes, enquanto a linha de cache L1 tem 64 bytes. Dessa forma, eu posso armazenar até 512 linhas de cache em L1. E se executarmos o mesmo benchmark com uma matriz de 512 elementos?
BenchmarkMatrixCombination-512 1404 718594 ns/op
BenchmarkMatrixReversedCombination-512 1363 850141 ns/opp
Embora tenhamos corrigido a diferença (em uma matriz de 64k, a diferença era cerca de 4 vezes), ainda podemos notar uma pequena diferença. O que pode estar errado? Nos benchmarks, trabalhamos com duas matrizes. Portanto, o processador deve manter as linhas de cache de ambos. Em um mundo ideal (nenhum outro aplicativo em execução e assim por diante), o cache L1 é preenchido 50% com dados da primeira matriz e 50% da segunda. E se reduzíssemos o tamanho da matriz pela metade para trabalhar com 256 elementos:
BenchmarkMatrixCombination-256 5712 176415 ns/op
BenchmarkMatrixReversedCombination-256 6470 164720 ns/op
Finalmente, chegamos ao ponto em que os dois resultados são (quase) equivalentes.
. ? , Go. - LEA (Load Effective Address). , . LEA .
, int64 , LEA , 8 . , . , . , () .
Agora - como limitar o impacto de falhas de cache no caso de uma matriz maior? Existe um método, chamado de otimização de loops aninhados (otimização de ninho de loop). Para tirar o máximo proveito das linhas de cache, devemos iterar apenas dentro de um determinado bloco.
Vamos definir um bloco no nosso exemplo como um quadrado de 4 elementos. Na primeira matriz, iteramos de (4.0) a (4.3). Em seguida, passe para a próxima linha. Dessa forma, iteramos sobre a segunda matriz apenas de (0,4) a (3,4) antes de passar para a próxima coluna.
Quando o ponteiro rosa passa pela primeira coluna, o processador armazena a linha de cache correspondente. Assim, revisar o resto do bloco significa tirar proveito de L1:
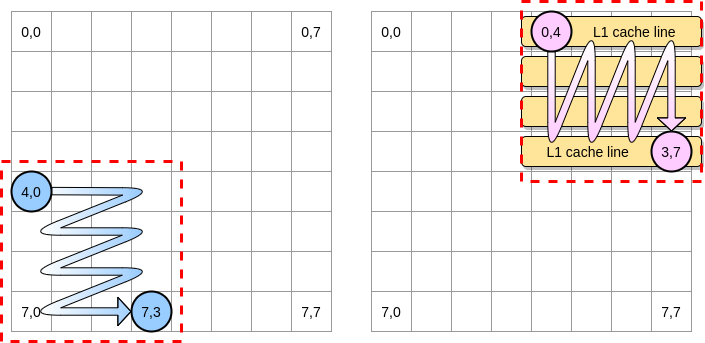
Vamos escrever uma implementação desse algoritmo no Go, mas primeiro devemos escolher cuidadosamente o tamanho do bloco. No exemplo anterior, era igual à linha de cache. Não deve ser menor, caso contrário, armazenaremos elementos que não serão acessíveis.
Em nosso benchmark Go, armazenamos elementos int64 (8 bytes cada). A linha de cache é de 64 bytes, portanto, pode conter 8 itens. Então o valor do tamanho do bloco deve ser pelo menos 8:
func BenchmarkMatrixReversedCombinationPerBlock(b *testing.B){
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
blockSize := 8
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i += blockSize {
for j := 0; j < matrixLength; j += blockSize {
for ii := i; ii < i+blockSize; ii++ {
for jj := j; jj < j+blockSize; jj++ {
matrixA[ii][jj] = matrixA[ii][jj] + matrixB[jj][ii]
}
}
}
}
}
}
Nossa implementação agora é 67% mais rápida do que quando iteramos por toda a linha / coluna:
BenchmarkMatrixReversedCombination-64000 2 573121540 ns/op
BenchmarkMatrixReversedCombinationPerBlock-64000 6 185375690 ns/op
Este foi o primeiro exemplo a demonstrar que o entendimento da operação dos caches da CPU pode ajudar a projetar algoritmos mais eficientes.
Compartilhamento falso
Agora entendemos como o processador gerencia caches internos. Como um resumo rápido:
- O princípio da localidade por distância força o processador a pegar não apenas um endereço de memória, mas uma linha de cache.
- O cache L1 é local para um núcleo do processador.
Agora vamos discutir um exemplo com a coerência do cache L1. A memória principal armazena duas variáveis
var1e var2. Um encadeamento em um núcleo acessa var1, enquanto outro encadeamento no outro núcleo acessa var2. Supondo que as duas variáveis sejam contínuas (ou quase contínuas), acabamos em uma situação em que ela está var2presente nos dois caches.
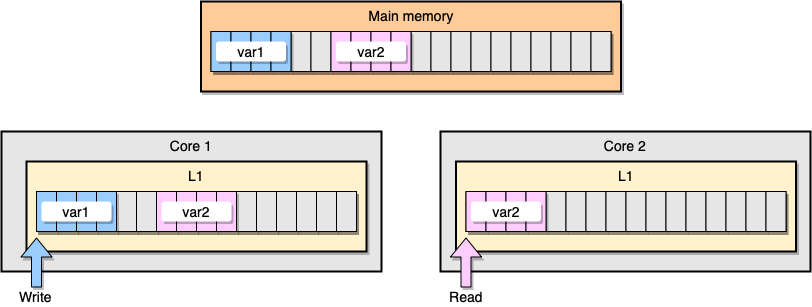
Exemplo de cache L1
O que acontece se o primeiro thread atualizar sua linha de cache? Pode potencialmente atualizar qualquer local de sua string, inclusive
var2. Em seguida, quando o segundo segmento for lido var2, o valor poderá não ser consistente.
Como o processador mantém o cache coerente? Se duas linhas de cache tiverem endereços compartilhados, o processador as marcará como compartilhadas. Se um segmento modifica uma linha compartilhada, marca ambos como modificados. É necessária coordenação entre núcleos para garantir a coerência dos caches, o que pode prejudicar significativamente o desempenho do aplicativo. Esse problema é chamado de compartilhamento falso .
Vamos considerar um aplicativo Go específico. Neste exemplo, criamos duas estruturas uma após a outra. Portanto, essas estruturas devem ser seqüenciais na memória. Em seguida, criamos duas goroutines, cada uma delas referente à sua própria estrutura (M é uma constante igual a um milhão):
type SimpleStruct struct {
n int
}
func BenchmarkStructureFalseSharing(b *testing.B) {
structA := SimpleStruct{}
structB := SimpleStruct{}
wg := sync.WaitGroup{}
b.ResetTimer()
for i := 0; i < b.N; i++ {
wg.Add(2)
go func() {
for j := 0; j < M; j++ {
structA.n += j
}
wg.Done()
}()
go func() {
for j := 0; j < M; j++ {
structB.n += j
}
wg.Done()
}()
wg.Wait()
}
}
Neste exemplo, a variável n da segunda estrutura está disponível apenas para a segunda goroutina. No entanto, como as estruturas são contíguas na memória, a variável estará presente nas duas linhas de cache (assumindo que as duas goroutines estejam agendadas em threads em núcleos separados, o que não é necessariamente o caso). Aqui está o resultado do benchmark:
BenchmarkStructureFalseSharing 514 2641990 ns/op
Como evitar o compartilhamento de informações falsas? Uma solução é a memória completa (preenchimento de memória). Nosso objetivo é garantir que haja espaço suficiente entre duas variáveis para que elas pertençam a diferentes linhas de cache.
Primeiro, vamos criar uma alternativa para a estrutura anterior preenchendo a memória após declarar a variável:
type PaddedStruct struct {
n int
_ CacheLinePad
}
type CacheLinePad struct {
_ [CacheLinePadSize]byte
}
const CacheLinePadSize = 64
Em seguida, instanciamos as duas estruturas e continuamos acessando essas duas variáveis em goroutines separadas:
func BenchmarkStructurePadding(b *testing.B) {
structA := PaddedStruct{}
structB := SimpleStruct{}
wg := sync.WaitGroup{}
b.ResetTimer()
for i := 0; i < b.N; i++ {
wg.Add(2)
go func() {
for j := 0; j < M; j++ {
structA.n += j
}
wg.Done()
}()
go func() {
for j := 0; j < M; j++ {
structB.n += j
}
wg.Done()
}()
wg.Wait()
}
}
Da perspectiva da memória, este exemplo deve parecer que as duas variáveis fazem parte de diferentes linhas de cache:
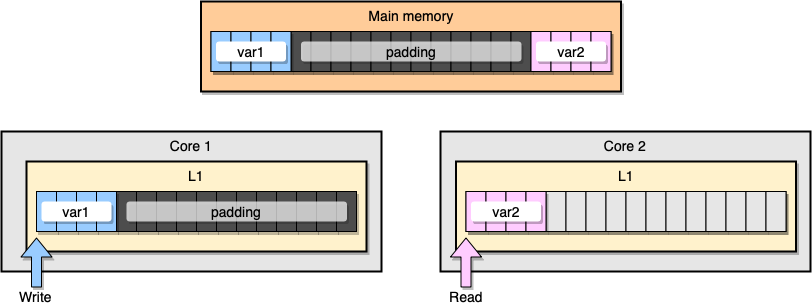
Preenchimento de memória
Vamos analisar os resultados:
BenchmarkStructureFalseSharing 514 2641990 ns/op
BenchmarkStructurePadding 735 1622886 ns/op
Um segundo exemplo com preenchimento de memória é cerca de 40% mais rápido que nossa implementação original. Mas também há uma desvantagem. O método acelera o código, mas requer mais memória.
Gostar de mecânica é um conceito importante quando se trata de otimizar aplicativos. Neste artigo, vimos exemplos de como o entendimento da CPU nos ajudou a melhorar a velocidade do programa.
O que mais se pode ler: