O aprendizado de máquina (ML) já está mudando o mundo. O Google usa o IO para oferecer e exibir respostas às pesquisas dos usuários. A Netflix o utiliza para recomendar filmes para a noite. E o Facebook usa para sugerir novos amigos que você talvez conheça.
O aprendizado de máquina nunca foi tão importante e, ao mesmo tempo, tão difícil de aprender. Essa área é cheia de jargões e o número de diferentes algoritmos de ML está aumentando a cada ano.
Este artigo apresentará conceitos fundamentais no aprendizado de máquina. Mais especificamente, discutiremos os conceitos básicos dos 9 algoritmos de ML mais importantes atualmente.
Sistema de recomendação
Construir um sistema completo de recomendações a partir de 0 requer profundo conhecimento de álgebra linear. Por esse motivo, se você nunca estudou essa disciplina, pode ser difícil entender alguns dos conceitos desta seção.
Mas não se preocupe - a biblioteca Python scikit-learn facilita a criação de um CP. Portanto, você não precisa desse conhecimento profundo de álgebra linear para criar um CP funcional.
Como o CP funciona?
Existem 2 tipos principais de sistemas de recomendação:
- Baseado em conteúdo
- Filtragem colaborativa
Um sistema baseado em conteúdo faz recomendações com base na semelhança dos elementos que você já usou. Esses sistemas se comportam exatamente da maneira que você espera que o PC se comporte.
A filtragem colaborativa de CP fornece recomendações baseadas no conhecimento de como o usuário interage com os elementos (* nota: as interações com elementos de outros usuários com comportamento semelhante ao do usuário são tomadas como base). Em outras palavras, eles usam a "sabedoria da multidão" (daí a "colaboração" no nome do método).
No mundo real, a filtragem colaborativa de CP é muito mais comum que um sistema baseado em conteúdo. Isto é principalmente devido ao fato de que eles geralmente dão melhores resultados. Alguns especialistas também acham o sistema colaborativo mais fácil de entender.
A filtragem colaborativa da CP também possui um recurso exclusivo não encontrado em um sistema baseado em conteúdo. Ou seja, eles têm a capacidade de aprender recursos por conta própria.
Isso significa que eles podem começar a definir similaridade em elementos com base em propriedades ou características que você nem forneceu para que este sistema funcionasse.
Existem 2 subcategorias de filtragem colaborativa:
- Baseado em modelo
- Bairro baseado
A boa notícia é que você não precisa saber a diferença entre esses dois tipos de filtragem de CP colaborativa para obter sucesso no ML. Basta saber que existem vários tipos.
Resumir
Aqui está uma rápida recapitulação do que aprendemos sobre o sistema de recomendações neste artigo:
- Exemplos de sistemas de recomendação do mundo real
- Diferentes tipos de sistema de recomendação e por que a filtragem colaborativa é usada com mais frequência do que o sistema baseado em conteúdo
- A relação entre sistema de recomendação e álgebra linear
Regressão linear
A regressão linear é usada para prever algum valor y com base em um conjunto de valores x.
História de regressão linear
A regressão linear (LR) foi inventada em 1800 por Francis Galton. Galton era um cientista estudando o vínculo entre pais e filhos. Mais especificamente, Galton investigou a relação entre o crescimento dos pais e o crescimento de seus filhos. A primeira descoberta de Galton foi o fato de que o crescimento dos filhos era, em regra, o mesmo que o crescimento de seus pais. O que não é surpreendente.
Mais tarde, Galton descobriu algo mais interessante. O crescimento do filho, em regra, estava mais próximo da altura média geral de todas as pessoas do que do crescimento de seu próprio pai.
Galton chamou esse fenômeno de regressão . Especificamente, ele disse: "A altura do filho tende a regredir (ou mudar para) a altura média".
Isso levou a um campo inteiro em estatística e aprendizado de máquina chamado regressão.
Regressão Linear Matemática
No processo de criação de um modelo de regressão, tudo o que tentamos fazer é desenhar uma linha o mais próximo possível de cada ponto do conjunto de dados.
Um exemplo típico dessa abordagem é a abordagem de regressão linear dos "mínimos quadrados", que calcula a proximidade de uma linha na direção de cima para baixo.
Exemplo de ilustração:
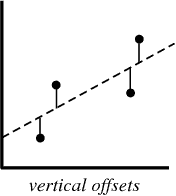
Quando você cria um modelo de regressão, seu produto final é uma equação que você pode usar para prever os valores de y para o valor de x sem conhecer o valor de y com antecedência.
Regressão logística
A regressão logística é semelhante à regressão linear, exceto que, em vez de calcular o valor de y, avalia a qual categoria um determinado ponto de dados pertence.
O que é regressão logística?
A regressão logística é um modelo de aprendizado de máquina usado para resolver problemas de classificação.
Abaixo estão alguns exemplos das tarefas de classificação do MO:
- Spam de email (spam ou não spam?)
- Reivindicação de seguro automóvel (compensação ou reparação?)
- Diagnóstico de doenças
Cada uma dessas tarefas possui claramente 2 categorias, tornando-as exemplos de tarefas de classificação binária.
A regressão logística funciona bem para problemas de classificação binária - simplesmente atribuímos categorias diferentes a 0 e 1, respectivamente.
Por que regressão logística? Porque você não pode usar regressão linear para previsões de classificação binária. Simplesmente não funcionará, pois você tentará desenhar uma linha reta através de um conjunto de dados com dois valores possíveis.
Esta imagem pode ajudá-lo a entender por que a regressão linear é ruim para a classificação binária:
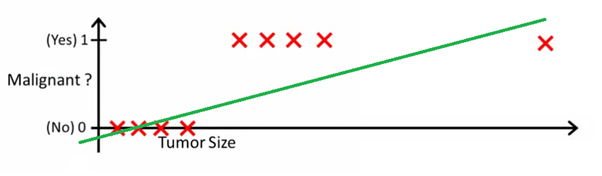
Nesta imagem, o eixo y representa a probabilidade de o tumor ser maligno. Os valores 1-y representam a probabilidade de o tumor ser benigno. Como você pode ver, o modelo de regressão linear apresenta um desempenho muito ruim para prever a probabilidade da maioria das observações no conjunto de dados.
É por isso que o modelo de regressão logística é útil. Ele tem uma inclinação para a linha de melhor ajuste, o que o torna muito mais adequado para prever dados qualitativos (categóricos).
Aqui está um exemplo que compara modelos de regressão linear e logística com os mesmos dados:
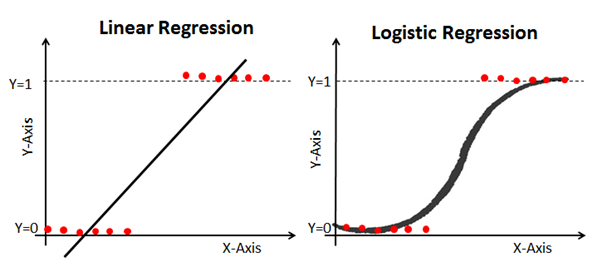
Sigmoide (a função sigmoide)
A razão pela qual a regressão logística é dobrada é porque ela não usa uma equação linear para calculá-la. Em vez disso, o modelo de regressão logística é construído usando um sigmóide (também chamado de função logística porque é usado na regressão logística).
Você não precisa memorizar completamente o sigmóide para ter sucesso no ML. Ainda assim, será útil ter uma idéia desse recurso.
Fórmula sigmóide: a
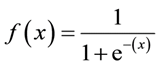
principal característica de um sigmóide, com o qual vale a pena lidar - não importa qual valor você passe para essa função, ele sempre retornará um valor entre 0-1.
Usando um modelo de regressão logística para previsões
Para usar a regressão logística para previsões, geralmente é necessário definir com precisão o ponto de corte. Esse ponto de corte é geralmente 0,5.
Vamos usar nosso exemplo de diagnóstico de câncer do gráfico anterior para ver esse princípio em prática. Se o modelo de regressão logística retornar um valor abaixo de 0,5, esse ponto de dados será categorizado como benigno. Da mesma forma, se o sigmóide fornecer um valor acima de 0,5, o tumor será classificado como maligno.
Usando uma matriz de erros para medir a eficácia da regressão logística
A matriz de erros pode ser usada como uma ferramenta para comparar as pontuações verdadeiro positivo, verdadeiro negativo, falso positivo e falso negativo no MO.
A matriz de erros é particularmente útil quando usada para medir o desempenho de um modelo de regressão logística. Aqui está um exemplo de como podemos usar a matriz de erro:
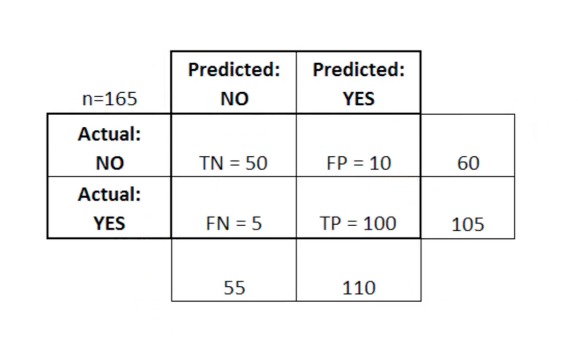
Nesta tabela, TN significa negativo verdadeiro, FN significa falso negativo, FP significa falso positivo, TP significa falso positivo, TP significa verdadeiro positivo.
Uma matriz de erros é útil para avaliar um modelo se houver quadrantes "fracos" na matriz de erros. Como exemplo, ela pode ter um número anormalmente alto de falsos positivos.
Em alguns casos, também é bastante útil garantir que seu modelo esteja funcionando corretamente em uma área particularmente perigosa da matriz de erros.
Neste exemplo de diagnóstico de câncer, por exemplo, você deseja garantir que seu modelo não tenha muitos falsos positivos porque isso significa que você diagnosticou o tumor maligno de alguém como benigno.
Resumir
Nesta seção, você conheceu o modelo ML - regressão logística.
Aqui está um rápido resumo do que você aprendeu sobre a regressão logística:
- Tipos de problemas de classificação adequados para resolução com regressão logística
- A função logística (sigmóide) sempre fornece um valor entre 0 e 1
- Como usar pontos de corte para prever com um modelo de regressão logística
- Por que uma matriz de erros é útil para medir o desempenho de um modelo de regressão logística
Algoritmo K-vizinhos mais próximos
O algoritmo k-vizinhos mais próximos pode ajudar a resolver o problema de classificação no caso em que existem mais de 2 categorias.
Qual é o algoritmo k-vizinhos mais próximos?
Este é um algoritmo de classificação baseado em um princípio simples. De fato, o princípio é tão simples que é melhor demonstrá-lo com um exemplo.
Imagine que você tem dados de altura e peso para jogadores de futebol e jogadores de basquete. O algoritmo k-vizinhos mais próximos pode ser usado para prever se um novo jogador é um jogador de futebol ou de basquete. Para isso, o algoritmo determina os pontos de dados K mais próximos do objeto de estudo.
Esta imagem demonstra esse princípio com o parâmetro K = 3:
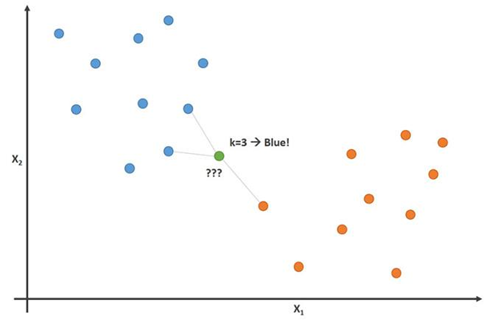
Nesta imagem, jogadores de futebol são azuis e jogadores de basquete são laranja. O ponto que estamos tentando classificar é colorido em verde. Como a maioria das (2 de 3) marcas mais próximas ao ponto verde é colorida em azul (jogadores de futebol), o algoritmo K-vizinhos mais próximos prevê que o novo jogador também será jogador de futebol.
Como construir um algoritmo K-vizinhos mais próximos
As principais etapas para criar esse algoritmo:
- Colete todos os dados
- Calcular a distância euclidiana do novo ponto de dados x até todos os outros pontos no conjunto de dados
- Classificar pontos do conjunto de dados em ordem crescente de distância até x
- Preveja a resposta usando a mesma categoria da maioria dos dados K-mais próximos de x
Importância da variável K no algoritmo K-vizinhos mais próximos
Embora isso possa não ser óbvio desde o início, alterar o valor K neste algoritmo alterará a categoria na qual o novo ponto de dados se enquadra.
Mais especificamente, um valor K muito baixo fará com que seu modelo preveja com precisão no conjunto de dados de treinamento, mas seja extremamente ineficaz nos dados de teste. Além disso, ter um K muito alto tornará o modelo desnecessariamente complexo.
A ilustração abaixo mostra esse efeito perfeitamente:
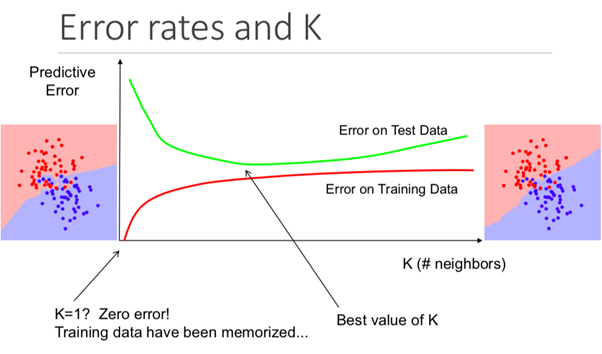
Prós e contras do algoritmo K-vizinhos mais próximos
Para resumir nossa introdução a esse algoritmo, vamos discutir brevemente os prós e os contras de usá-lo.
Prós:
- O algoritmo é simples e fácil de entender
- Treinamento de modelo trivial em novos dados de treinamento
- Funciona com qualquer número de categorias em uma tarefa de classificação
- Adicione facilmente mais dados a muitos dados
- O modelo usa apenas 2 parâmetros: K e a métrica de distância que você gostaria de usar (geralmente distância euclidiana)
Minuses:
- Alto custo de computação, porque você precisa processar toda a quantidade de dados
- Não funciona tão bem com parâmetros categóricos
Resumir
Um resumo do que você acabou de aprender sobre o algoritmo K-vizinho mais próximo:
- Um exemplo de problema de classificação (jogadores de futebol ou basquete) que o algoritmo pode resolver
- Como o algoritmo usa a distância euclidiana dos pontos vizinhos para prever a qual categoria um novo ponto de dados pertence
- Por que os valores de K são importantes para a previsão
- Prós e contras do uso do algoritmo K-vizinhos mais próximos
Árvores de decisão e florestas aleatórias
Árvore de decisão e floresta aleatória são 2 exemplos de um método de árvore. Mais precisamente, as árvores de decisão são modelos de ML usados para prever percorrendo cada função em um conjunto de dados, um por um. Uma floresta aleatória é um conjunto (comitê) de árvores de decisão que usam ordens aleatórias de objetos em um conjunto de dados.
O que é um método de árvore?
Antes de mergulharmos nos fundamentos teóricos do método baseado em árvore no ML, é útil começar com um exemplo.
Imagine que você está jogando basquete toda segunda-feira. Além disso, você sempre convida o mesmo amigo para vir brincar com você. Às vezes um amigo vem, às vezes não. A decisão de vir ou não depende de muitos fatores: que tipo de clima, temperatura, vento e fadiga. Você começa a perceber esses recursos e acompanhá-los junto com a decisão de seu amigo de jogar ou não.
Você pode usar esses dados para prever se seu amigo está chegando hoje ou não. Uma técnica que você pode usar é uma árvore de decisão. É assim:
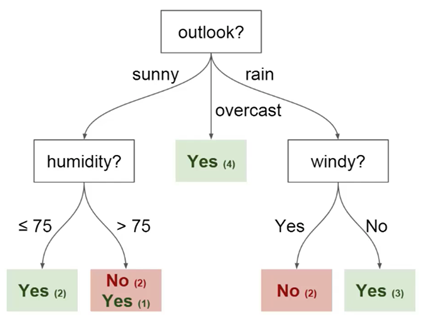
Cada árvore de decisão possui 2 tipos de elementos:
- Nós: locais onde a árvore é dividida com base no valor de um determinado parâmetro
- Arestas: o resultado da divisão que leva ao próximo nó
Você pode ver que o diagrama possui nós para perspectivas, umidade e
vento. E também as facetas de cada valor potencial de cada um desses parâmetros.
Aqui estão mais algumas definições que você deve entender antes de começarmos:
- Raiz - o nó a partir do qual a divisão da árvore começa
- Folhas - os nós finais que prevêem o resultado final
Agora você tem um entendimento básico do que é uma árvore de decisão. Veremos como construir uma árvore desse tipo a partir do zero na próxima seção.
Como construir uma árvore de decisão a partir do zero
Construir uma árvore de decisão é mais complicado do que parece. Isso ocorre porque decidir em quais ramificações (características) os dados serão divididos (que é um tópico de entropia e aquisição de dados) é uma tarefa matematicamente desafiadora.
Para resolver esse problema, os especialistas em ML geralmente usam muitas árvores de decisão, aplicando conjuntos aleatórios de características escolhidas para dividir a árvore nelas. Em outras palavras, novos conjuntos aleatórios de características são escolhidos para cada árvore separada, em cada partição separada. Essa técnica é chamada de florestas aleatórias.
Em geral, os especialistas geralmente escolhem o tamanho de um conjunto aleatório de recursos (indicado por m) para que seja a raiz quadrada do número total de recursos no conjunto de dados (indicado por p). Em resumo, m é a raiz quadrada de p e, em seguida, uma característica específica é selecionada aleatoriamente a partir de m.
Benefícios do uso de uma floresta aleatória
Imagine que você está trabalhando com muitos dados que possuem uma característica "forte". Em outras palavras, há uma característica nesse conjunto de dados que é muito mais previsível em termos de resultado final do que outras características desse conjunto de dados.
Se você estiver construindo uma árvore de decisão manualmente, faz sentido usar essa característica para a partição "superior" da sua árvore. Isso significa que você terá várias árvores cujas previsões são altamente correlacionadas.
Queremos evitar isso porque o uso da média de variáveis altamente correlacionadas não reduz significativamente a variação. Usando conjuntos aleatórios de características para cada árvore em uma floresta aleatória, correlacionamos as árvores e a variação do modelo resultante é reduzida. Essa correlação é uma grande vantagem no uso de florestas aleatórias sobre árvores de decisão construídas à mão.
Resumir
Então, aqui está um rápido resumo do que você acabou de aprender sobre árvores de decisão e florestas aleatórias:
- Um exemplo de um problema cuja solução pode ser prevista usando uma árvore de decisão
- Elementos da árvore de decisão: nós, faces, raízes e folhas
- Como o uso de um conjunto aleatório de características nos permite construir uma floresta aleatória
- Por que usar uma floresta aleatória para decorrelação de variáveis pode ser útil na redução da variação do modelo resultante
Máquinas de vetores de suporte
Máquinas de vetores de suporte são um algoritmo de classificação (embora, tecnicamente falando, elas também possam ser usadas para resolver problemas de regressão) que divide um conjunto de dados em categorias nas maiores "lacunas" entre categorias. Esse conceito fica mais claro quando você olha para o exemplo a seguir.
O que é uma máquina de vetores de suporte?
Uma máquina de vetor de suporte (SVM) é um modelo de ML supervisionado com algoritmos de aprendizado apropriados que analisam dados e reconhecem padrões. O SVM pode ser usado para tarefas de classificação e análise de regressão. Neste artigo, examinaremos especificamente o uso de máquinas de vetores de suporte para resolver problemas de classificação.
Como o MOU funciona?
Vamos aprofundar o funcionamento do MOU.
Recebemos um conjunto de exemplos de treinamento, cada um deles marcado como pertencente a uma das 2 categorias e, usando esse conjunto de SVMs, construímos um modelo. Este modelo categoriza novos exemplos em uma de duas categorias. Isso torna o SVM um classificador linear binário improvável.
O MOU usa geometria para fazer previsões por categoria. Mais especificamente, a máquina de vetores de suporte mapeia pontos de dados como pontos no espaço e os categoriza para que sejam separados pelo maior espaço possível. A previsão de que novos pontos de dados pertencerão a uma categoria específica é baseada em qual lado do ponto de interrupção está.
Aqui está um exemplo de visualização para ajudar você a entender a intuição do MOU:
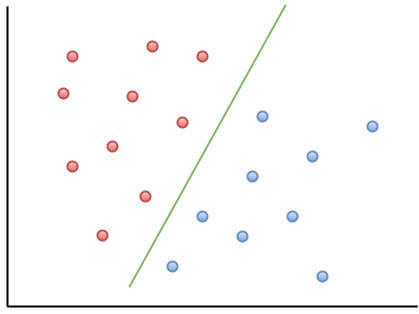
Como você pode observar, se um novo ponto de dados cair à esquerda da linha verde, ele será chamado de "vermelho" e, à direita, será chamado de "azul". Essa linha verde é chamada de hiperplano e é um termo importante para trabalhar com MOUs.
Vamos dar uma olhada na seguinte representação visual do SVM:
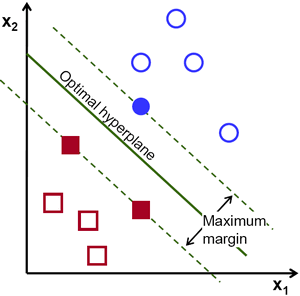
Neste diagrama, o hiperplano é rotulado como o "hiperplano ideal". A teoria da máquina de vetores de suporte define um hiperplano ideal como um hiperplano que maximiza o campo entre os dois pontos de dados mais próximos de diferentes categorias.
Como você pode ver, o limite do campo realmente afeta 3 pontos de dados - 2 da categoria vermelha e 1 da azul. Esses pontos, que estão em contato com a borda do campo, são chamados vetores de suporte - daí o nome.
Resumir
Aqui está uma rápida visão geral do que você acabou de aprender sobre máquinas de vetores de suporte:
- O MOU é um exemplo de algoritmo de ML supervisionado
- O vetor de suporte pode ser usado para resolver problemas de classificação e para análise de regressão.
- Como o MOU categoriza dados usando um hiperplano que maximiza a margem entre categorias no conjunto de dados
- Os pontos de dados que tocam os limites do campo de divisão são chamados vetores de suporte. É daí que o nome do método vem.
K-Means Clustering
O método K-Means é um algoritmo de aprendizado de máquina não supervisionado. Isso significa que ele aceita dados não marcados e tenta agrupar clusters de observações semelhantes nos seus dados. O método K-Means é extremamente útil para resolver aplicativos do mundo real. Aqui estão exemplos de várias tarefas que se encaixam nesse modelo:
- Segmentação de clientes para equipes de marketing
- Classificação de documentos
- Otimizando rotas de remessa para empresas como Amazon, UPS ou FedEx
- Identificação e resposta a locais criminosos na cidade
- Análise profissional de esportes
- Prever e prevenir o cibercrime
O principal objetivo do método K-Means é dividir o conjunto de dados em grupos distinguíveis para que os elementos em cada grupo sejam semelhantes entre si.
Aqui está uma representação visual da aparência na prática:
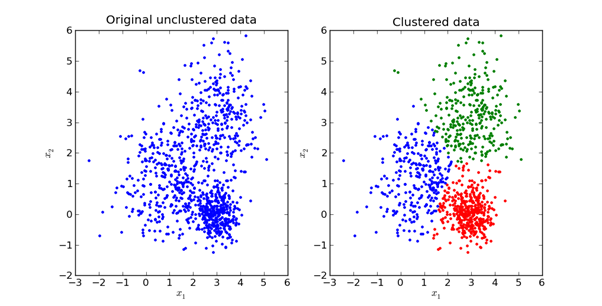
Exploraremos a matemática por trás do método K-Means na próxima seção deste artigo.
Como o método K-Means funciona?
A primeira etapa do uso do método K-Means é escolher o número de grupos nos quais você deseja dividir seus dados. Essa quantidade é o valor de K, refletido no nome do algoritmo. A escolha do valor K no método K-Means é muito importante. Discutiremos como escolher o valor correto K. Mais tarde
, você deve selecionar aleatoriamente um ponto no conjunto de dados e atribuí-lo a um cluster aleatório. Isso fornecerá a posição de dados inicial na qual você executa a próxima iteração até que os clusters parem de mudar:
- Calculando o centróide (centro de gravidade) de cada aglomerado, tomando o vetor médio dos pontos desse aglomerado
- Reatribua cada ponto de dados ao cluster cujo centróide está mais próximo do ponto
Escolhendo um valor K apropriado no método K-Means
A rigor, escolher um valor K adequado é bastante difícil. Não existe uma resposta "certa" na escolha do "melhor" valor de K. Um método que os profissionais de ML costumam usar é chamado de "método do cotovelo".
Para usar esse método, a primeira coisa que você precisa fazer é calcular a soma dos erros ao quadrado - o desvio padrão do seu algoritmo para um grupo de valores K. O desvio padrão no método K-means é definido como a soma dos quadrados das distâncias entre cada ponto de dados no cluster. e o centro de gravidade deste aglomerado.
Como exemplo desta etapa, você pode calcular o desvio padrão para os valores de K de 2, 4, 6, 8 e 10. Em seguida, você deseja gerar um gráfico do desvio padrão e desses valores de K. Você verá que o desvio diminui à medida que o valor de K aumenta.
E faz sentido: quanto mais categorias você criar a partir de um conjunto de dados, maior a probabilidade de cada ponto de dados estar próximo ao centro do cluster desse ponto.
Dito isso, a principal idéia por trás do método do cotovelo é escolher o valor de K no qual o RMS diminuirá drasticamente a taxa de declínio. Esse declínio acentuado forma um "cotovelo" no gráfico.
Como exemplo, aqui está um gráfico de RMS em relação a K. Nesse caso, o método do cotovelo sugerirá o uso de um valor K de cerca de 6.
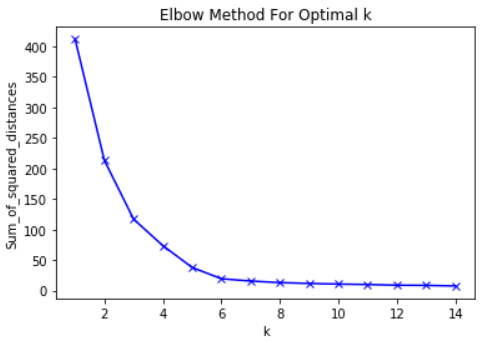
É importante que K = 6 seja simplesmente uma estimativa de um valor aceitável de K. Não existe um "melhor" valor de K no método K-Means. Como muitas coisas no ML, essa é uma decisão muito situacional.
Resumir
Aqui está um rápido esboço do que você acabou de aprender nesta seção:
- Exemplos de tarefas de BC sem um professor que podem ser resolvidos pelo método K-means
- Princípios básicos do método K-means
- Como funciona o K-Means
- Como usar o método cotovelo para selecionar o valor apropriado para o parâmetro K neste algoritmo
Análise do componente principal
A análise de componentes principais é usada para transformar um conjunto de dados com muitos parâmetros em um novo conjunto de dados com menos parâmetros, e cada novo parâmetro nesse conjunto de dados é uma combinação linear de parâmetros existentes anteriormente. Esses dados transformados tendem a justificar grande parte da variação do conjunto de dados original com muito mais simplicidade.
O que é o método do componente principal?
A análise de componentes principais (ACP) é uma técnica de ML usada para estudar as relações entre conjuntos de variáveis. Em outras palavras, o PCA examina conjuntos de variáveis para determinar a estrutura básica dessas variáveis. O PCA também é chamado de análise fatorial.
Com base nessa descrição, você pode pensar que o PCA é muito semelhante à regressão linear. Mas esse não é o caso. De fato, essas duas técnicas têm várias diferenças importantes.
Diferenças entre regressão linear e PCA
A regressão linear determina a linha de melhor ajuste no conjunto de dados. A análise de componentes principais identifica várias linhas ortogonais de melhor ajuste para um conjunto de dados.
Se você não estiver familiarizado com o termo ortogonal, significa simplesmente que as linhas estão em ângulos retos entre si, como norte, leste, sul e oeste em um mapa.
Vejamos um exemplo para ajudar você a entender isso melhor.

Veja os rótulos dos eixos nesta imagem. O principal componente do eixo x explica 73% da variação neste conjunto de dados. O principal componente do eixo y explica cerca de 23% da variação no conjunto de dados.
Isso significa que 4% da variação permanece inexplicável. Você pode reduzir esse número adicionando mais componentes principais à sua análise.
Resumir
Um resumo do que você acabou de aprender sobre a análise de componentes principais:
- O PCA tenta encontrar fatores ortogonais que determinam a variabilidade em um conjunto de dados
- Diferença entre regressão linear e PCA
- Como são os principais componentes ortogonais quando renderizados em um conjunto de dados
- Que a adição de componentes principais adicionais pode ajudar a explicar a variação com mais precisão no conjunto de dados