Classificação inferior da pilha

Este é o artigo final da série de classificação de heap. Nas palestras anteriores, vimos uma grande variedade de estruturas de pilha, mostrando excelentes resultados de velocidade. Isso levanta a questão: qual pilha é a mais eficiente quando se trata de classificação? A resposta é: a que olharemos hoje.

EDISON .




— « » — -, CRM-, , iOS Android.



;-)

Os montes sofisticados que examinamos anteriormente são bons, mas o heap mais eficiente é o heap padrão com limpeza aprimorada.



O que é uma limpeza, por que é necessário em uma pilha e como funciona é descrito na primeira parte de uma série de artigos.



A peneiração padrão na classificação clássica de um grupo funciona aproximadamente como "testa" - um elemento da raiz da subárvore é enviado para a área de transferência, enquanto os elementos do ramo, de acordo com os resultados da comparação, aumentam. É bastante simples, mas há muitas comparações.







Na faixa ascendente, as comparações são salvas devido ao fato de os pais dificilmente serem comparados aos seus descendentes; basicamente, apenas os descendentes são comparados entre si. Em um amontoado comum, os pais são comparados com os filhos e os filhos são comparados entre si - portanto, há quase uma vez e meia mais comparações com o mesmo número de trocas.



Então, como funciona, vamos ver um exemplo específico. Digamos que temos uma matriz na qual um monte está quase formado - tudo o que resta é peneirar a raiz. Para todos os outros nós, a condição é atendida - qualquer descendente não é mais que seu pai.



Primeiro, no nó para o qual a peneiração é realizada, é necessário descer ao longo dos descendentes grandes. A pilha é binária - ou seja, temos um filho esquerdo e um filho certo. Descemos para o ramo onde o descendente é maior. Nesta fase, a maioria das comparações ocorre - as crianças esquerda / direita são comparadas entre si.







Tendo alcançado a folha no último nível, decidimos, assim, o ramo, cujos valores precisam ser alterados. Mas você não precisa mover o ramo inteiro, mas apenas a parte que é maior que a raiz da qual você iniciou.



Portanto, subimos a ramificação até o nó mais próximo, que é maior que a raiz.







O último passo - usando a variável de buffer, alteramos os valores dos nós no ramo.







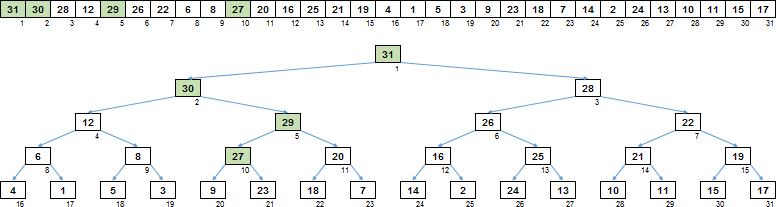
É isso aí. A peneira ascendente formou uma árvore de classificação a partir da matriz, na qual qualquer pai ou mãe é maior que seus descendentes.



Animação final:

Implementação Python 3.7

O algoritmo básico de classificação não é diferente do heapsort regular:

#    
def HeapSortBottomUp(data):

    #    
    #   -   
    # (   )       
    for start in range((len(data) - 2) // 2, -1, -1):
        HeapSortBottomUp_Sift(data, start, len(data) - 1) 

    #        
    #        .
    for end in range(len(data) - 1, 0, -1): 
        #       
        #    
        data[end], data[0] = data[0], data[end]
        #        
        #   
        #     
        HeapSortBottomUp_Sift(data, 0, end - 1)
    return data

A descida para a folha inferior é convenientemente / visualmente colocada em uma função separada:

#      
#   
def HeapSortBottomUp_LeafSearch(data, start, end):
    
    current = start
    
    #  ,  
    #  (  ) 
    while True:
        child = current * 2 + 1 #  
        #  ,    
        if child + 1 > end: 
            break 
        #  ,   
        if data[child + 1] > data[child]:
            current = child + 1
        else:
            current = child
    
    #  ,    
    child = current * 2 + 1 #  
    if child <= end:
        current = child
        
    return current

E o mais importante - uma clareira, primeiro descendo e depois emergindo para cima:

#  
def HeapSortBottomUp_Sift(data, start, end):
    
    #        
    current = HeapSortBottomUp_LeafSearch(data, start, end)
    
    #  ,    
    #     
    while data[start] > data[current]:
        current = (current - 1) // 2
    
    #   ,
    #      
    temp = data[current]
    data[current] = data[start]
    
    #        
    # -     
    while current > start:
        current = (current - 1) // 2
        temp, data[current] = data[current], temp  

Puramente empiricamente - de acordo com minhas medidas, a classificação ascendente por um monte funciona 1,5 vezes mais rápido que a classificação regular por um monte.



De acordo com algumas informações (na página do algoritmo da Wikipedia, no PDF citado na seção "Links"), o BottomUp HeapSort está em média à frente de uma classificação ainda mais rápida - para matrizes bastante grandes de 16 mil elementos ou mais.

Ligações

Heapsort de baixo para cima Uma variante do Heapsort com número quase ideal de comparações



Criando montões rapidamente



Uma nova variante do heapsort superando, em média, o quicksort (se n não for muito pequeno)

Artigos da série:

• Aplicativo Excel AlgoLab.xlsm
• Classificando trocas
• Classificar inserções
• Classificação de seleção
  • Tipos de pilhas: N-pirâmides
  • Heap Sort: Leonardo Numbers
  • Classificações da pilha: Pilha fraca
  • Heap classifica: árvore cartesiana
  • Classificações de Heap: Árvore de Torneios
  • Classificação de heap: compensação ascendente
• Mesclar classificações
• Classificar por distribuição
• Classificações híbridas

A classificação de hoje foi adicionada ao aplicativo AlgoLab, que a utiliza - atualize o arquivo do Excel com macros.