FAISS: Pesquise rapidamente rostos e clones em dados multimilionários

Certa vez, na véspera de uma conferência de clientes realizada anualmente pelo grupo DAN, ponderamos que coisas interessantes poderiam ser pensadas para que nossos parceiros e clientes tivessem impressões e lembranças agradáveis ​​do evento. Decidimos analisar um arquivo de milhares de fotos desta conferência e várias anteriores (e havia 18 delas naquela época): uma pessoa nos envia sua foto e, em alguns segundos, enviamos a ele uma seleção de fotos de nossos arquivos por vários anos.



Nós não inventamos uma bicicleta, pegamos a conhecida biblioteca dlib e recebemos incorporações (representações vetoriais) de cada pessoa. 



Adicionamos um bot do Telegram por conveniência, e tudo foi ótimo. Do ponto de vista dos algoritmos de reconhecimento de face, tudo funcionou bem, mas a conferência terminou e eu não queria me separar de tecnologias testadas e comprovadas. Queríamos passar de milhares de pessoas a centenas de milhões, mas não tínhamos uma tarefa comercial específica. Depois de algum tempo, nossos colegas tiveram uma tarefa que exigia trabalhar com quantidades tão grandes de dados.



A questão era escrever um sistema inteligente de monitoramento de bots no Instagram. Aqui nosso pensamento deu origem a uma abordagem simples e complexa:



Maneira simples: consideramos todas as contas que têm muito mais assinaturas que assinantes, nenhum avatar, nome completo não é preenchido etc. Como resultado, temos uma multidão incompreensível de contas meio mortas.



O caminho difícil: como os robôs modernos se tornaram muito mais inteligentes e agora publicam, dormem e até escrevem conteúdo, surge a pergunta: como capturá-los? Em primeiro lugar, monitore de perto os amigos, pois eles também são bots e acompanhe fotos duplicadas. Em segundo lugar, raramente qualquer bot sabe como gerar suas próprias imagens (embora isso seja possível), o que significa que fotos duplicadas de pessoas em contas diferentes no Instagram são um bom gatilho para encontrar uma rede de bots.

Qual é o próximo?

Se um caminho simples é bastante previsível e rapidamente dá alguns resultados, então um caminho difícil é difícil justamente porque para implementá-lo, teremos que vetorizar e indexar volumes incrivelmente grandes de fotografias para comparações subsequentes de similaridades - milhões e até bilhões. Como colocá-lo em prática? Afinal, surgem problemas técnicos:

1. Velocidade e precisão da pesquisa
2. Espaço em disco usado pelos dados
3. O tamanho da memória RAM usada. 

Se houvesse apenas algumas fotos, pelo menos não mais que dez mil, poderíamos nos limitar a soluções simples com agrupamento de vetores, mas trabalhar com grandes volumes de vetores e encontrar os vizinhos mais próximos de um determinado vetor, são necessários algoritmos complexos e otimizados.



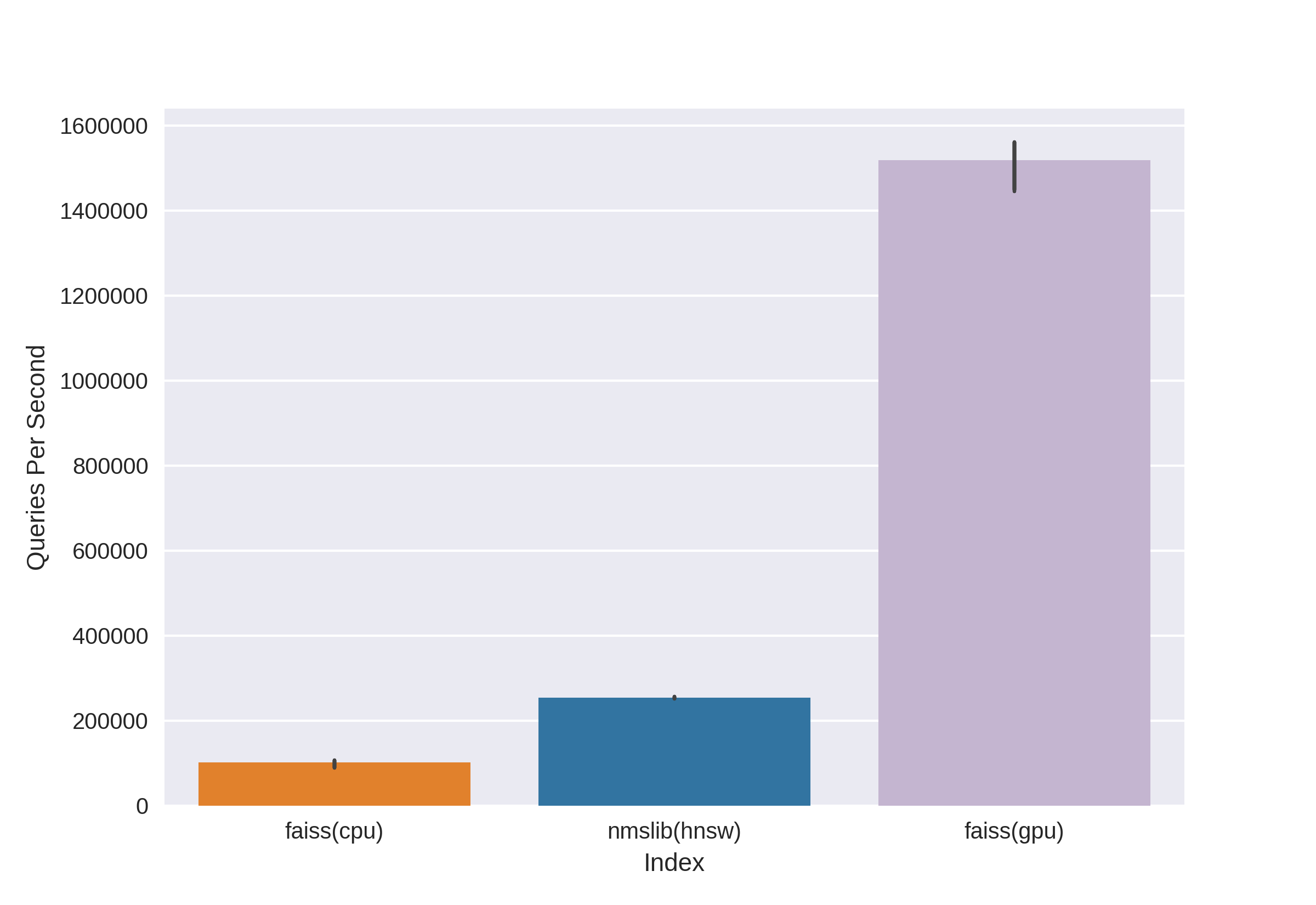
Existem tecnologias conhecidas e comprovadas, como Annoy, FAISS, HNSW. Rápido HNSW vizinho lookup algoritmo disponível no nmslib e bibliotecas hnswlib, mostra resultados de última geração na CPU, que podem ser vistos nos mesmos benchmarks. Mas nós o cortamos imediatamente, pois não estamos satisfeitos com a quantidade de memória usada ao trabalhar com grandes quantidades de dados. Começamos a escolher entre Annoy e FAISS e, no final, escolhemos FAISS por conveniência, menos uso de memória, uso potencial na GPU e benchmarks de desempenho (você pode ver, por exemplo, aqui ). A propósito, no FAISS, o algoritmo HNSW é implementado como uma opção.

O que é FAISS?

A Pesquisa de similaridade de pesquisa do AI do Facebook é um desenvolvimento da equipe de Pesquisa do AI do Facebook para encontrar rapidamente vizinhos próximos e agrupar no espaço vetorial. A alta velocidade de pesquisa permite trabalhar com dados muito grandes - até vários bilhões de vetores.



A principal vantagem do FAISS são os resultados mais avançados da GPU, enquanto sua implementação na CPU perde um pouco para hnsw (nmslib). Queríamos poder pesquisar na CPU e na GPU. Além disso, o FAISS é otimizado em termos de uso de memória e pesquisa em grandes lotes.



O



FAISS de origem permite encontrar rapidamente os k vetores mais próximos para um determinado vetor x. Mas como essa pesquisa funciona sob o capô?

Índices

O principal conceito do FAISS é índice e, em essência, é apenas uma coleção de parâmetros e vetores. Conjuntos de parâmetros são completamente diferentes e dependem das necessidades do usuário. Os vetores podem permanecer inalterados, mas podem ser reconstruídos. Alguns índices estão disponíveis para o trabalho imediatamente após a adição de vetores e alguns requerem treinamento preliminar. Os nomes de vetores são armazenados no índice: na numeração de 0 a n ou como um número que se encaixa no tipo Int64.



O primeiro índice, e o mais simples que usamos na conferência, é o Flat . Ele armazena apenas todos os vetores em si, e a pesquisa de um determinado vetor é realizada por pesquisa exaustiva, portanto, não há necessidade de treiná-lo (mas mais sobre o treinamento abaixo). Com uma pequena quantidade de dados, um índice tão simples pode cobrir totalmente as necessidades da pesquisa.



Exemplo:

import numpy as np
dim = 512  #     512
nb = 10000  #    
nq = 5 #      
np.random.seed(228)
vectors = np.random.random((nb, dim)).astype('float32')
query = np.random.random((nq, dim)).astype('float32')

Crie um índice simples e adicione vetores sem treinamento:

import faiss
index = faiss.IndexFlatL2(dim)
print(index.ntotal)  #   
index.add(vectors)
print(index.ntotal)  #    10 000 

Agora encontramos 7 vizinhos mais próximos para os cinco primeiros vetores de vetores:

topn = 7
D, I = index.search(vectors[:5], topn)  #  : Distances, Indices
print(I)
print(D)

Vemos que os vizinhos mais próximos com uma distância de 0 são os próprios vetores, o resto é variado pelo aumento da distância. Vamos procurar nossos vetores da consulta:

D, I = index.search(query, topn) 
print(I)
print(D)

Agora, as distâncias na primeira coluna dos resultados não são zero, pois os vetores da consulta não estão no índice.



O índice pode ser salvo no disco e, em seguida, carregado no disco:

faiss.write_index(index, "flat.index")
index = faiss.read_index("flat.index")

Parece que tudo é elementar! Algumas linhas de código - e já temos uma estrutura para pesquisar vetores de alta dimensão. Mas esse índice com apenas dez milhões de vetores da dimensão 512 pesará cerca de 20 GB e consumirá a mesma quantidade de RAM ao usá-lo.



No projeto da conferência, usamos apenas uma abordagem tão básica com um índice plano, tudo foi ótimo devido à quantidade relativamente pequena de dados, mas agora estamos falando de dezenas e centenas de milhões de vetores de alta dimensão!

Acelere sua pesquisa com listas invertidas

Fonte



O principal e mais interessante recurso do FAISS é o índice de fertilização in vitro ouíndice de arquivo invertido . A idéia dos arquivos invertidos é lacônica e lindamente explicada nos dedos :



vamos imaginar um exército gigantesco, composto pelos guerreiros mais heterogêneos, numerando, digamos, 1.000.000 de pessoas. Será impossível comandar todo o exército de uma só vez. Como é habitual em assuntos militares, precisamos dividir nosso exército em subunidades. Vamos dividir em$$$\sqrt{1 000 000} = 1000$partes aproximadamente iguais, escolhendo para o papel de comandantes um representante de cada unidade. E tentaremos enviar os caracteres mais semelhantes, origem, dados físicos etc. soldados em uma unidade, e selecionamos o comandante para que ele represente sua unidade com a maior precisão possível - ele era alguém "médio". Como resultado, nossa tarefa foi reduzida do comando de um milhão de soldados para o comando das milésimas unidades através de seus comandantes, e temos uma excelente ideia da composição de nosso exército, pois sabemos o que são comandantes.



Esta é a idéia por trás do índice de fertilização in vitro: vamos agrupar um grande conjunto de vetores peça por peça usando o algoritmo k-means, colocando correspondência em cada parte um centróide, é um vetor que é o centro escolhido para um determinado cluster. A busca será realizada através da distância mínima até o centróide, e somente então procuraremos as distâncias mínimas entre os vetores no cluster que correspondem ao centróide especificado. Tomando k igual$$$\sqrt{n}$Onde $$$n$ - o número de vetores no índice, obteremos uma pesquisa ideal em dois níveis - primeiro entre $$$\sqrt{n}$ centróide, então entre $$$\sqrt{n}$vetores em cada cluster. A pesquisa, comparada à pesquisa exaustiva, é acelerada várias vezes, o que resolve um dos nossos problemas ao trabalhar com muitos milhões de vetores.





O espaço vetorial é dividido pelo método k-means em k clusters. Cada conjunto é atribuído um centróide.



Código Exemplo:

dim = 512
k = 1000  #  “”
quantiser = faiss.IndexFlatL2(dim) 
index = faiss.IndexIVFFlat(quantiser, dim, k)
vectors = np.random.random((1000000, dim)).astype('float32')  # 1 000 000 “”

Ou você pode anotá-la com muito mais elegância, usando a prática ferramenta FAISS para criar um índice:

index = faiss.index_factory(dim, “IVF1000,Flat”)
 :
print(index.is_trained)   # False.
index.train(vectors)  # Train    
 
#  ,      ,      :
print(index.is_trained)  # True
print(index.ntotal)   # 0
index.add(vectors)
print(index.ntotal)   # 1000000

Depois de examinar esse tipo de índice após o Flat, resolvemos um de nossos possíveis problemas - a velocidade da pesquisa, que se torna várias vezes menor em comparação à pesquisa exaustiva.

D, I = index.search(query, topn) 
print(I)
print(D)

Mas existe um "mas" - a precisão da pesquisa, bem como a velocidade, dependerão do número de clusters visitados, que podem ser configurados usando o parâmetro nprobe:

print(index.nprobe)  # 1 –           
index.nprobe = 16  #   -16    top-n  
D, I = index.search(query, topn) 
print(I)
print(D)

Como você pode ver, depois de aumentar o nprobe, temos resultados completamente diferentes, o topo das distâncias mais curtas em D se tornou melhor.



Você pode usar nprobe igual ao número de centróides no índice; isso será equivalente à pesquisa por pesquisa exaustiva; a precisão será maior, mas a velocidade da pesquisa diminuirá visivelmente.

Pesquisando no disco - Listas invertidas no disco

Ótimo, resolvemos o primeiro problema, agora obtemos uma velocidade de pesquisa aceitável em dezenas de milhões de vetores! Mas tudo isso é inútil, contanto que nosso enorme índice não se ajuste à RAM.



Especificamente para a nossa tarefa, a principal vantagem do FAISS é a capacidade de armazenar índices de FIV de listas invertidas no disco, carregando apenas metadados na RAM.



Como criamos um índice desse tipo: treinamos o indexIVF com os parâmetros necessários na quantidade máxima possível de dados que entra na memória, depois adicionamos vetores ao índice treinado em partes (tendo sido treinados e não apenas) e gravamos o índice de cada uma das partes no disco.

index = faiss.index_factory(512, “,IVF65536, Flat”, faiss.METRIC_L2)

O treinamento do índice GPU é realizado da seguinte maneira:

res = faiss.StandardGpuResources()
index_ivf = faiss.extract_index_ivf(index)
index_flat = faiss.IndexFlatL2(512)
clustering_index = faiss.index_cpu_to_gpu(res, 0, index_flat)  #  0 –  GPU
index_ivf.clustering_index = clustering_index

faiss.index_cpu_to_gpu (res, 0, index_flat) pode ser substituído por faiss.index_cpu_to_all_gpus (index_flat) para usar todas as GPUs juntas.



É altamente desejável que a amostra de treinamento seja o mais representativa possível e tenha uma distribuição uniforme, para que possamos compor o conjunto de dados de treinamento antecipadamente a partir do número necessário de vetores, selecionando-os aleatoriamente no conjunto de dados inteiro.

train_vectors = ...  #     
index.train(train_vectors)

#    ,   :
faiss.write_index(index, "trained_block.index") 

#       
#      :
for bno in range(first_block, last_block+ 1):
    block_vectors = vectors_parts[bno]
    block_vectors_ids = vectors_parts_ids[bno]  # id ,  
    index = faiss.read_index("trained_block.index")
    index.add_with_ids(block_vectors, block_vectors_ids)
    faiss.write_index(index, "block_{}.index".format(bno))

Depois disso, combinamos todas as listas invertidas. Isso é possível, já que cada um dos blocos é, de fato, o mesmo índice treinado, apenas com vetores diferentes.

ivfs = []
for bno in range(first_block, last_block+ 1):
    index = faiss.read_index("block_{}.index".format(bno), faiss.IO_FLAG_MMAP)
    ivfs.append(index.invlists)
    #  index   inv_lists 
    #        :
    index.own_invlists = False

#   :
index = faiss.read_index("trained_block.index")

#   invlists
#  invlists       merged_index.ivfdata
invlists = faiss.OnDiskInvertedLists(index.nlist, index.code_size, "merged_index.ivfdata")
ivf_vector = faiss.InvertedListsPtrVector() 

for ivf in ivfs: 
    ivf_vector.push_back(ivf)

ntotal = invlists.merge_from(ivf_vector.data(), ivf_vector.size())
index.ntotal = ntotal  #     
index.replace_invlists(invlists)  
faiss.write_index(index, data_path + "populated.index")  #    

Conclusão: agora nosso índice é populated.index e arquivos merged_blocks.ivfdata .



Em populated.index registrou o caminho completo original para o arquivo com as Listas Invertidas, portanto, se o caminho do arquivo ivfdata, por algum motivo, a alteração na leitura do índice precisar usar a bandeira faiss.IO_FLAG_ONDISK_SAME_DIR , que permite procurar o arquivo ivfdata no mesmo diretório que o populated.index:

index = faiss.read_index('populated.index', faiss.IO_FLAG_ONDISK_SAME_DIR)

O exemplo de demonstração do projeto Github FAISS foi tomado como base .



Um mini-guia para escolher um índice pode ser encontrado no Wiki da FAISS . Por exemplo, conseguimos colocar um conjunto de dados de treinamento de 12 milhões de vetores na RAM, por isso escolhemos o índice IVFFlat em 262144 centróides e, em seguida, escalamos para centenas de milhões. Também é proposto o uso do índice IVF262144_HNSW32 no guia, no qual a afiliação de um vetor a um cluster é determinada pelo algoritmo HNSW com 32 vizinhos mais próximos (em outras palavras, usando o quantizador IndexHNSWFlat), mas, como nos parecia em outros testes, a pesquisa por esse índice é menos precisa. Além disso, deve-se ter em mente que esse quantizador elimina a possibilidade de uso na GPU.

Reduza drasticamente o uso do disco com a quantização do produto

Graças ao método de pesquisa de disco, foi possível remover a carga da RAM, mas o índice com um milhão de vetores ainda ocupava cerca de 2 GB de espaço em disco, e estamos discutindo a possibilidade de trabalhar com bilhões de vetores, o que exigiria mais de dois TB! Obviamente, o volume não é tão grande se você definir uma meta e alocar espaço em disco adicional, mas isso nos incomodou um pouco.



E aqui a codificação vetorial vem em socorro, a saber: Quantização Escalar (SQ) e Quantização de Produto (PQ)... SQ é a codificação de cada componente vetorial com n bits (geralmente 8, 6 ou 4 bits). Vamos considerar a opção PQ, porque a idéia de codificar um único componente do tipo float32 com oito bits parece muito deprimente em termos de precisão. Embora em alguns casos a compactação do SQfp16 para float16 seja quase sem perda de precisão.



A essência da quantização do produto é a seguinte: os vetores da dimensão 512 são divididos em n partes, cada uma das quais é agrupada em 256 possíveis agrupamentos (1 byte), ou seja, nós representamos um vetor com n bytes, onde n é geralmente no máximo 64 em uma implementação FAISS. Mas essa quantização é aplicada não aos próprios vetores do conjunto de dados, mas às diferenças desses vetores e dos centróides correspondentes obtidos no estágio de geração de Listas Invertidas! Acontece que as Listas Invertidas serão conjuntos codificados de distâncias entre vetores e seus centróides.

index = faiss.index_factory(dim, "IVF262144,PQ64", faiss.METRIC_L2)

Acontece que agora não é necessário armazenar todos os vetores - basta alocar n bytes por vetor e 2048 bytes por cada vetor de centróide. No nosso caso, pegamos$$$n = 64$, ou seja $$$\frac{512}{64} = 8$- o comprimento de um subvetor, definido em um dos 256 clusters.







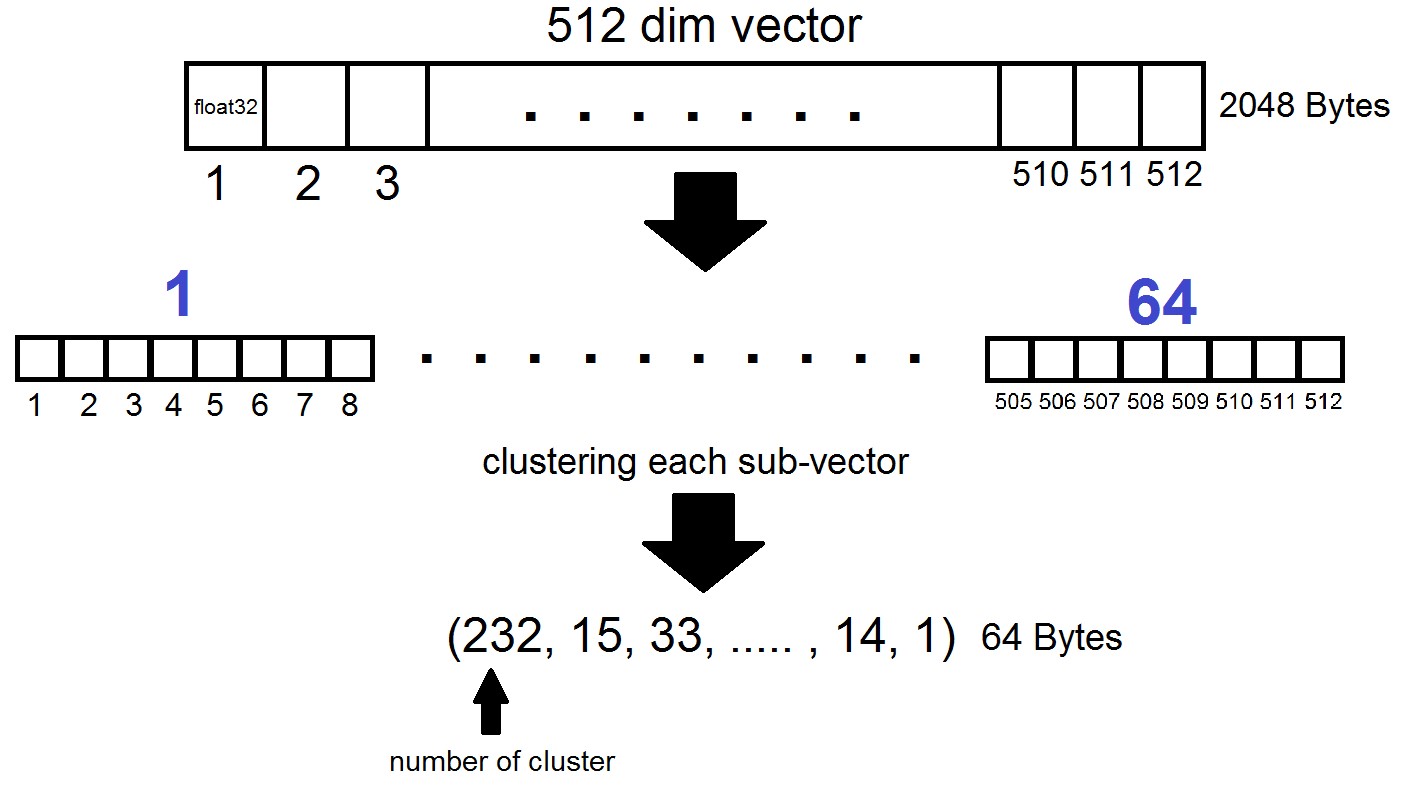
Ao pesquisar pelo vetor x, os centróides mais próximos serão determinados primeiro com o quantizador plano usual e, em seguida, x também será dividido em subvectores, cada um dos quais é codificado pelo número de um dos 256 centróides correspondentes. E a distância para o vetor é definida como a soma de 64 distâncias entre os sub-vetores.

Qual é o resultado?

Interrompemos nossos experimentos no índice “IVF262144, PQ64”, uma vez que satisfazia completamente todas as nossas necessidades de velocidade e precisão da pesquisa, além de garantir o uso razoável do espaço em disco com redimensionamento adicional do índice. Mais especificamente, no momento, com 315 milhões de vetores, o índice ocupa 22 GB de espaço em disco e cerca de 3 GB de RAM em uso.



Outro detalhe interessante que não mencionamos anteriormente é a métrica usada pelo índice. Por padrão, as distâncias entre dois vetores são calculadas na métrica Euclidean L2 ou, em linguagem mais compreensível, as distâncias são calculadas como a raiz quadrada da soma dos quadrados das diferenças em coordenadas. Mas você pode definir outra métrica, em particular, testamos a métrica METRIC_INNER_PRODUCT, ou métrica das distâncias do cosseno entre vetores. É cosseno porque o cosseno do ângulo entre dois vetores no sistema de coordenadas euclidianas é expresso como a proporção do produto escalar (coordenado) dos vetores para o produto de seus comprimentos, e se todos os vetores em nosso espaço tiverem comprimento 1, o cosseno do ângulo será exatamente igual ao produto em coordenadas. Nesse caso, quanto mais próximos os vetores estiverem no espaço, mais próximo da unidade estará o produto escalar.



A métrica L2 tem uma transição matemática direta para a métrica do produto escalar. No entanto, ao comparar experimentalmente as duas métricas, a impressão era de que a métrica de produtos escalares nos ajuda a analisar os coeficientes de similaridade das imagens de maneira mais bem-sucedida. Além disso, os incorporamentos de nossas fotos foram obtidos usandoInsightFace , que implementa a arquitetura ArcFace usando distâncias de cosseno. Também existem outras métricas nos índices FAISS que você pode ler aqui .

Conclusão e exemplos interessantes

Então, de volta para onde tudo começou. E tudo começou, lembramos, com a motivação para resolver o problema de encontrar bots na rede do Instagram e, mais especificamente - procure postagens duplicadas com pessoas ou avatares em determinados conjuntos de usuários. No processo de redação do material, ficou claro que uma descrição detalhada de nossa metodologia para procurar bots exigiria um artigo separado, que discutiremos nas publicações a seguir, mas, por enquanto, nos limitaremos a exemplos de nossos experimentos com o FAISS.



Você pode vetorizar imagens ou rostos de maneiras diferentes. Escolhemos a tecnologia InsightFace (vetorizar imagens e extrair recursos n-dimensionais delas é uma longa história separada). No decorrer de experimentos com a infraestrutura que recebemos, foram descobertas propriedades bastante interessantes e engraçadas.



Por exemplo, tendo garantido a permissão de colegas e conhecidos, colocamos seus rostos na pesquisa e encontramos rapidamente as fotografias nas quais eles estão presentes:





Nosso colega tirou uma foto de um visitante da Comic-Con, estando no fundo no meio de uma multidão. Faça um





piquenique de origem em um grande grupo de amigos, foto da conta de um amigo. Fonte





Apenas de passagem. Um fotógrafo desconhecido capturou os caras por seu perfil temático. Eles não sabiam para onde foi a foto e depois de cinco anos se esqueceram completamente de como foram fotografados. Fonte





Nesse caso, o fotógrafo é desconhecido e fotografado secretamente!

Lembrou imediatamente a garota suspeita com SLR, sentada no momento em frente a :) Fonte



Assim, através de ações simples, o FAISS permite coletar no joelho um análogo do conhecido FindFace.



Outra característica interessante: no índice FAISS, quanto mais as faces são semelhantes, mais próximas são os vetores correspondentes no espaço. Eu decidi dar uma olhada nos resultados de pesquisa um pouco menos precisos no meu rosto e encontrei clones terrivelmente parecidos comigo :)





Alguns dos clones do autor.

Fontes fotográficas: 1 , 2 ,  3



De um modo geral, a FAISS abre um campo enorme para a implementação de quaisquer idéias criativas. Por exemplo, usando o mesmo princípio de proximidade vetorial de faces semelhantes, é possível construir caminhos de uma pessoa para outra. Ou, como último recurso, faça do FAISS uma fábrica para a produção de tais memes:





Fonte



Obrigado por sua atenção e esperamos que este material seja útil para os leitores da Habr!



Este artigo foi escrito com o apoio de meus colegas Artyom Korolyov (korolevart), Timur Kadyrov e Arina Reshetnikova.



Rede de Pesquisa e Desenvolvimento Dentsu Aegis Russia.